一种靶场关键段姿态交会测量优化布站分析方法

胡小丽，唐明刚，蔡文泽，张玉伦，张思琪，张三喜

(1 63875部队，陕西 华阴 714200；2 西安现代控制技术研究所，西安 710065)

0 引言

靶场典型目标关键段姿态测量通常采取沿关键段弹道中心对称布站方式，通常布站主要考虑分站成像像长大于60像素，认为满足常规精度测试需求，则可对称布站测量；此种布站方式对于具有一定高度的平飞段，虽然精度可控，但不能确保其为最佳精度布站点；而对于主动段、攻击段等低高度区，常规弹道中心对称布站方式严重影响测量精度，故必须寻求科学合理的优化布站分析方法。文献[1]依据经验对低空和高空目标给出了一些布站建议，但缺乏明确的优化布站理论依据。文献[2]对关键因素给出了数据分析和结论，但同样缺乏具体的理论分析。文献[3-6]主要研究弹道布站，对于姿态测量布站没有涉及。

文中以中轴线法为依托，分析中轴线交会法涉及的主要影响因素，根据平飞段及主动段的不同测量需求，对关键影响因素进行独立及联合规律分析，给出具体的计算模型，从而获取平飞段及主动段最佳对称布站点，为实际光学姿态测量提供理论依据。

1 布站方法分析

靶场光学姿态测量通常采用交会模式[7-8]，测量精度与布站及采用的处理方法密切相关。中轴线法[7]采用2个分站采集的轴线成像矢量进行交会，合成矢量经过解析获取所需的偏航和俯仰角，可以作为姿态测量的基础依据。又由于靶场光学姿态测量通常基于中远距离小视场，故对中轴线法略作矢量化改进，忽略轴线在分站成像截距信息，减小姿态处理影响因素，以此作为布站优劣的精度评估依据。

依据靶场典型目标的飞行特点对于姿态测量的不同需求，可将目标飞行段落分为两类：一类是平飞段，此时已处于稳定跟踪段，光学姿态测量系统通常可沿弹道侧方对称布站；另一类是发射、攻击段，由于目标速度变化及目标特性复杂，对设备跟踪要求相对提高，故此时布站要考虑一定距离之外的跟踪可信度。

1.1 布站优劣精度评估依据

设目标理论姿态角偏航角(ψ)、俯仰角(φ)已知。分站1光轴指向为(A1,E1)，分站2光轴指向为(A2,E2)，其中：A为光轴指向方位角；E为光轴指向俯仰角。目标中轴在分站1的像面倾角为ɑ1，目标中轴在分站2的像面倾角为ɑ2，像面倾角判读最大误差角为Δɑ2(此处设分站2为主要判读误差源)。坐标系基准以常规中轴线法为准。

以中轴线法为基准，获取测量坐标系下基于纯矢量合成(因靶场光学测姿作用距离多为千米级，光学镜头通常为长焦距小视场，故可忽略投影截距因素)中的l,m,n,Δl,Δm,Δn分量，其中，l，m，n分别为所求中轴线矢量的X，Y，Z方向分量；Δl,Δm,Δn为因分站图像倾角判读误差引起的X,Y,Z方向分量误差。又因靶场典型目标航迹基本平行于主靶道飞行，故平飞段中轴矢量集中于l分量，主动段和攻击段中轴矢量集中于l,m分量，Δm,Δn为偏航角和俯仰角精度的主要误差影响因素，故关键分量为l,m,Δm,Δn。则描述偏航角ψ、俯仰角φ的精度评估量值Δψ,Δφ为：

(1)

1.2 平飞段布站方法分析

平飞段特征：平行于主靶道，m=n=0,ψ=φ=0。

固定分站1于弹道侧方中心位置，则A1=90°，设分站2方位角为A2，E1=E2=E， 将中轴矢量向分站进行投影，联合中轴实际长度、物距和焦距信息可获取中轴模拟倾角α，以及物像投影比例及模拟中轴像长，则：

(2)

依据中轴线交会公式并以分站2判读误差为主要源头，可得：

(3)

(4)

由式(2)～式(4)可得：

(5)

由式(5)可知，低高度区偏航角、高高度区俯仰角精度是重点考虑因素，因交会重构的l的量值分别随E的变化非常接近于零值。故依据式(5)，平飞段布站结论为：

1)偏航角、俯仰角精度与E严格相关，当E>45°，偏航角精度优于俯仰角，反之，当E<45°，偏航角精度劣于俯仰角。

2)取E趋近于90°，考虑Δφ取极小值，则A=270°，即布站最佳位置弹道对称交会。

3)取E趋近于0°，考虑Δψ取极小值，则A为0°或180°，即布站最佳位置为90°交会。

4)尤其注意高高度区俯仰角以及低高度区偏航角精度量值，误差主要来源于交会算法本身的放大效果，故应用时应注意极限范围是否满足测试需求。

1.3 主动段、攻击段布站方法分析

初始主动段、末点攻击段平行于主靶道，n=0,ψ=0，E近似0，n=0,m=ltanφ, 固定分站1于弹道侧方中心位置，则A1=90°，设分站2方位角为A2，E1=E2=0， 将中轴矢量向分站进行投影，联合中轴实际长度、物距和焦距信息可获取中轴模拟倾角α，以及物像投影比例及模拟中轴像长，则：

(6)

依据中轴线交会公式并以分站2判读误差为主要源头，可得：

(7)

(8)

由式(6)～式(8)可得：

(9)

对式(9)在不同A下求极小值，可知A取0°或180°时，Δψ和Δφ可同时取极小值。

鉴于上述分析，初始主动段、末点攻击段结论为：

1)初始主动段、末点攻击段最佳布站位置为90°交会布站。

2)偏航角、俯仰角精度与A及φ严格相关。

3)不可对称弹道中心布站，因交会算法局限，此时偏航角精度不可控。

2 算法验证

2.1 平飞段布站

以某型目标平飞段为例，为验证不同高度随布站位置差异导致的精度差异，选取不同高度进行分析验证，距地面高度h取50 m,1 000 m,2 000 m,4 000 m，X设置为1 500～3 500 m,Z为0；固定分站1于对称弹道中心侧方位置，即X,Z为(2 500 m，-1 000 m)，A1=90°，目标偏航角ψ=0°、俯仰角φ=0°，将分站2的X,Z分别布设于(2 500 m， 1 000 m)、(1 400 m,10 m)、(1 800 m,700 m),相对站点1约为180°交会(弹道对称)、135°交会以及90°交会位置，通过式(1)计算，获取优化布站建议。

表1 距地50 m仿真验证结果

表2 距地1 000 m仿真验证结果

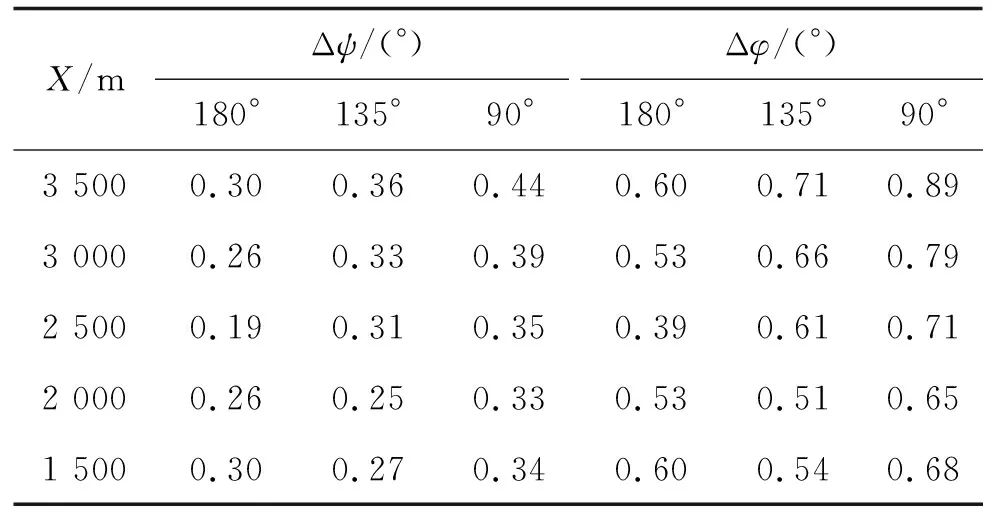
表3 距地2 000 m仿真验证结果

表4 距地4 000 m仿真验证结果

由表1～表4可知，平飞段布站结论为：

1) 偏航角精度与俯仰角精度随不同布站相对变化趋势一致，即同一弹道条件下，布站优则偏航角和俯仰角精度高。

2) 由于实际情况下弹道高度分站俯仰角通常远小于90°，故平飞段仅模拟了4 000 m以下高度，低高度区俯仰角精度为重要验证剖面，即50 m高度试验剖面。从结果可知，90°交会结果最优；随着高度的增加，4 000 m高度测量，180°精度最优，虽分站俯仰角远小于90°，但符合理论分析趋势，与前述理论分析结果一致。

3) 平飞段布站规律，实际测试高度通常小于4 000 m，低高度区偏航角为重点考虑因素，最佳布站为90°交会布站；随着高度升高，布站位置应向180°交会转移。

4) 具体实施应结合场地、弹道条件及目标特性等进行具体条件代入模拟。

2.2 主动段布站

以某型目标主动段为例，弹道上关键5点及ψ，φ设置如表5所示，按照主动段跟踪能力测试需求(目标最大速度28 m/s,按照半自动跟踪角速度不大于1°考虑)，则分站物距不小于1 500 m，为保证数据录取率，焦距选取小焦距1 500 mm，目标中轴长为2.45 m；按照平飞段的3种典型布站方式计算比较分析，确定主动段姿态交会测量优化布站方案。

表5 关键点信息设置

经式(1)计算，相应结果如表6所示。

表6 仿真验证结果

由表6可知主动段布站结论为：

1)在低高度区，偏航角精度为重点考虑因素，上述3种方式偏航角精度均劣于俯仰角精度。

2)90°布站为最佳布站，其它两种方式均劣于该种布站方式，尤其偏航角的误差均较大。

3)具体实施应结合场地、弹道条件及目标特性等进行具体条件代入模拟。

3 结论

以精度评估为布站优劣评价依据，根据平飞段及攻击段不同测试需求分析，总结了靶场布站的重要影响因子，通过分析影响因素对不同布站的规律，获取了靶场平飞段及主动段/攻击段优化布站建议，即低高度区最佳布站为90°交会布站，随着目标高度的增加，布站应重点考虑成像大小，即布站逐步向180°侧方对称布站转移，边界精度应以实际输入及场地、弹道代入计算为准，为实际姿态测量提供了布站的理论依据。