计算机仿真：从概念模型到心智模型——以高中物理电场建模教学为例

陈康

（福清元洪高级中学，福建 福清 350300）

高中物理作为基础学科，对于培养学生的科学素养具有不可替代的作用。物理概念是客观事物的共同物理属性和本质特征在人们头脑中的反映，是物理事物的抽象。概念学习对学生能力发展有着重要的价值。高中物理教育传统上注重传授概念的意义、内涵和外延，而忽视了学生对物理概念的主动建构。建构主义认为学习是一种能动建构的过程。一方面，研究者提出了各种概念转变理论以及“认知冲突”“脚手架”等具体教学策略，但是因为学生的迷思概念普遍而且顽固，无法一一纠正，教学效果并不令人特别满意。现有的概念转变理论研究都是从学习者的认知出发，科学概念本身常常被忽略。另外研究为数不多的基本科学概念转变所获得的理论缺乏普适性。［1］另一方面，建模理论吸收了认知科学的研究成果，同时关注了学科知识的结构要素，更合理地解释了认知建构的本质。［2］建模理论弱化转变和冲突，注重建构过程，［3］提供了教学策略。

以“静电场”为例，该模块在高中物理中的地位非常重要，是高考的重要考查内容。但是由于该模块概念繁多、十分抽象，学生难以理解各个概念间的逻辑关系。学习进阶可以描述学生的思维方式从新手到专家的发展路径。郭玉英教授仿照诺伊曼（Knut Neumann）等人的做法，将内容和认知相结合，构成二维进阶变量。认知方面分成五个层级：经验、映射、关联、概念、整合。［4］笔者参考新版课程标准，将内容方面分成两个层级：“静电场力的性质”与“静电场能的性质”，如表1 所示：

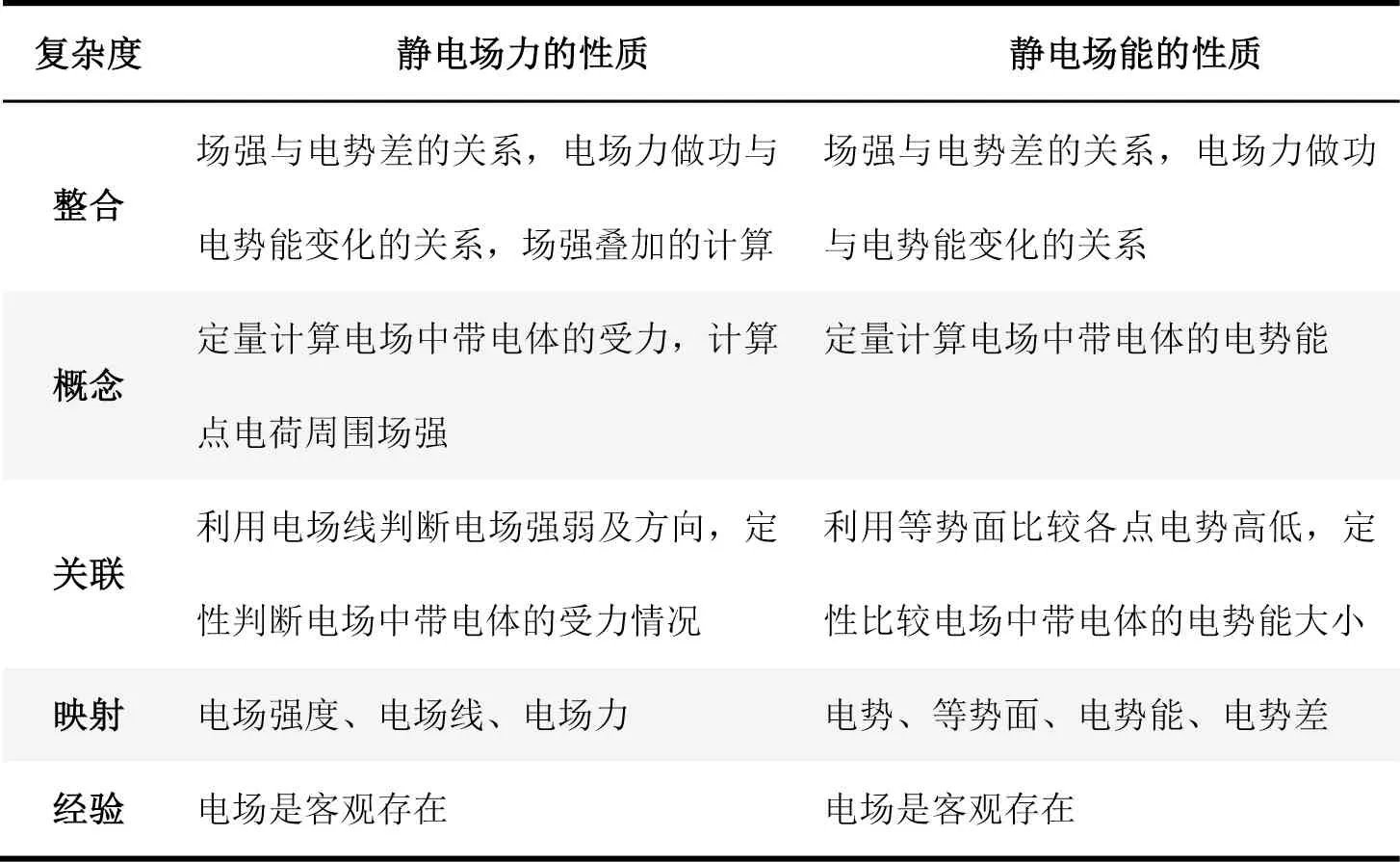
表1

学生通过学习，一般能够接受以下描述：利用电场线分布来描述场强，利用等势面分布来描述电势，电场线与等势面互相垂直。但是由于概念较多，学生容易混淆，比如难以理解电场线分布特征；又如即便认识到电场线由高电势指向低电势，还会错误地认为电场强度大的地方电势高。学生在学习过程中产生的迷思概念较多，教师很难一一纠正。

要完整地理解电场，必须将“静电场力的性质”“静电场能的性质”两个层级进行整合。学生不理解电场线分布特征，是因为没有熟练掌握电场叠加原理；学生不理解场强的强弱与电势高低无关，只与电势差有关，是因为没有真正理解Δφ=EΔx 这个公式（教师可以把匀强电场中的公式U=Ed 利用微元思想推广到非匀强电场得到Δφ=EΔx）。

一、理解真实世界只能通过建构心智模型来实现

赫斯滕斯（David Hestenes）从20 世纪80 年代起发展了科学教育中的建模理论。这个理论认为真实世界、概念模型与心智模型是不断循环、相互作用的：心智模型是指长时间记忆中的要素与外在情境或刺激物相互作用所产生的内在表征，是对事物的结构化类比，是个体根据特定目的形成的动态的认知结构。心智模型的特点是个人的、内隐的。概念模型是科学共同体创造出来用以客观描述与表征真实世界，而个体理解概念模型建构了主观的心智模型，此外，观察真实世界，也能帮助建构心智模型。［3］如图1 所示：

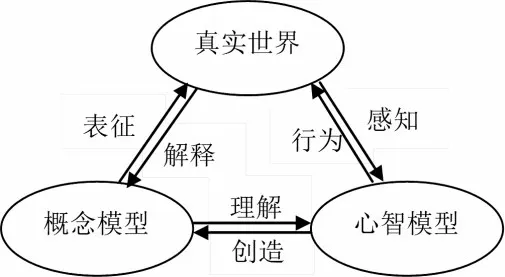
图1

新版新课程标准基于物理学科的本质提出了核心素养。物理学科核心素养前两个要素是“物理观念”与“科学思维”。［5］物理观念是物理概念和规律等在头脑中的提炼与升华；科学思维是人脑对客观事物的本质属性，内在规律与相互关系的认识方式，科学思维的第一个要素是模型建构。模型建构是指基于经验事实建构物理模型的抽象概括过程。［6］学生只有学会电场的模型建构，才能促进概念转变，达到整合，最终形成静电场的观念。建模教学是一个比较合适的教学模式。

建模教学理论认为专家是基于概念模型，利用数学方程等工具表征具体情境，进行推理。新手与专家的区别在于心智模型的正确性。认知心理学上，建模教学就是能帮助学生达到建立或修改原本所持有的心智模型目的的教学模式。诺尔曼（Donald Arthur Norman）认为课堂设计必须将专家的心智模型概念化，使学生与目标系统互动，不断修正和精致化他们的心智模型。［3］如图2 所示：

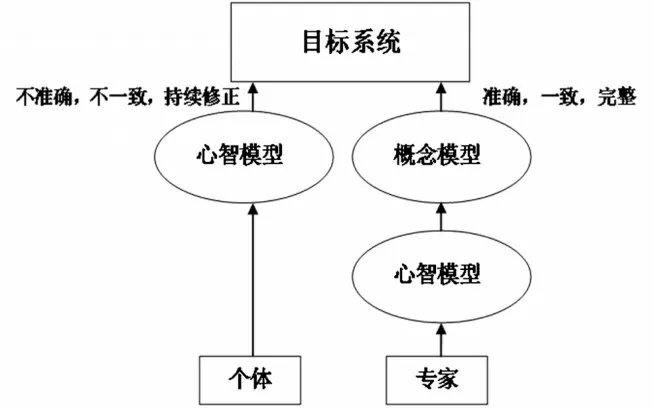
图2

心智模型是如何形成与发展的，目前并未真正解决。碎片观认为学生的概念是零散的，概念转变是建立概念间的联结。而整体一致观认为学生已经具有一个理论框架，概念转变是丰富和修正框架。［3］笔者认为个体的心智模型因人而异，可能与学生所处的学习进阶的层级有关。教师应该更关注选择合适的概念模型引导学生建构心智模型。

埃基纳（Eugenia Etkina）等人对物理教学中的模型作用进行了研究。他们将概念模型分为对象模型，相互作用模型，系统模型与过程模型（定性或定量）。建模过程就是将客观实体简化或理想化为概念模型，然后引入数学表征（如物理量，作用方程，状态方程，过程方程）进行表述。［3］静电场作为一种客观存在，可以视为对象模型，电场强度E、电势φ、电势差U 或Δφ都是它的数学表征。

概念模型表征了它们对应的真实世界，可以用实体、符号、图像、文字等多种形式表现。受载体制约，课本只能采用静态图像的方法展示电场特点。静态图像本质上可认为是专家的心智模型概念化，图中信息大。作为新手，学生存在太多迷思概念，很难一步到位地通过观察静态图像建构起科学的心智模型，所以无法理解电场线分布的成因，也无法理解场强的强弱与电势无关。计算机仿真可以替代静态图像，做到逐步展示建模的过程，引导学生转变概念，修正和精致化自己的心智模型。

二、利用计算机仿真进行建模教学，促进学生心智模型发展

哈伦（Ibrahim Halloun）提出建模教学五个阶段：模型选择，模型建立，模型验证，模型分析，模型调度。他认为五个阶段可能步骤会重叠，其中模型建立与分析是非常重要的活动，模型建立确认所选模型相关结构及成分，应当引导学生建立数学表征，模型分析用以解决问题并进行解释。在教学中通过互动与辩证，帮助学生发展其心智模型的有效性与迁移性。［3］在电场的概念模型中，点电荷公式E=，场强叠加原理，电场强度与电势差的关系式Δφ=EΔx 都是其数学表征。只有真正理解了这些表征，才能整合概念，形成观念。

笔者根据教学经验，认为在静电场授课完毕后，可以补充一节复习课进行建模教学，让学生观察计算机仿真演示，会获得更好的教学效果。计算机仿真可以将电场模型可视化，特别是可以展示概念模型的建模过程，帮助学生理解数学表征，建构心智模型。

矩阵实验室（MATLAB）是迈斯沃克（MathWorks）公司推出的用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境的商业数学软件。教师可以根据具体模型特点建立曲线或者曲线族，曲面，图像或者动画来展示各种模型，将其可视化。

笔者利用MATLAB 提供的函数进行了计算机仿真，实现了专家的电场心智模型的概念化，展示了专家的电场概念模型的建构过程。以下以等量同种正电荷周围电场分布建模为例，［7］试说明建模教学的各个阶段及计算机仿真方法：

（一）模型选择与建立

电场是一种特殊形式的物质，法拉第构想出“力线”模型来描述它，后续的科学家不断用数学公式进行表征。教科书上的静态图像就是来自法拉第的设想，计算机仿真可以更好地取代它的作用。（取q1=q2=1×10-9C，坐标单位为m）

理想的点电荷是没有体积的，作图时可用一个很小的圆来表示。作出电荷q1与q2。如图3 所示：

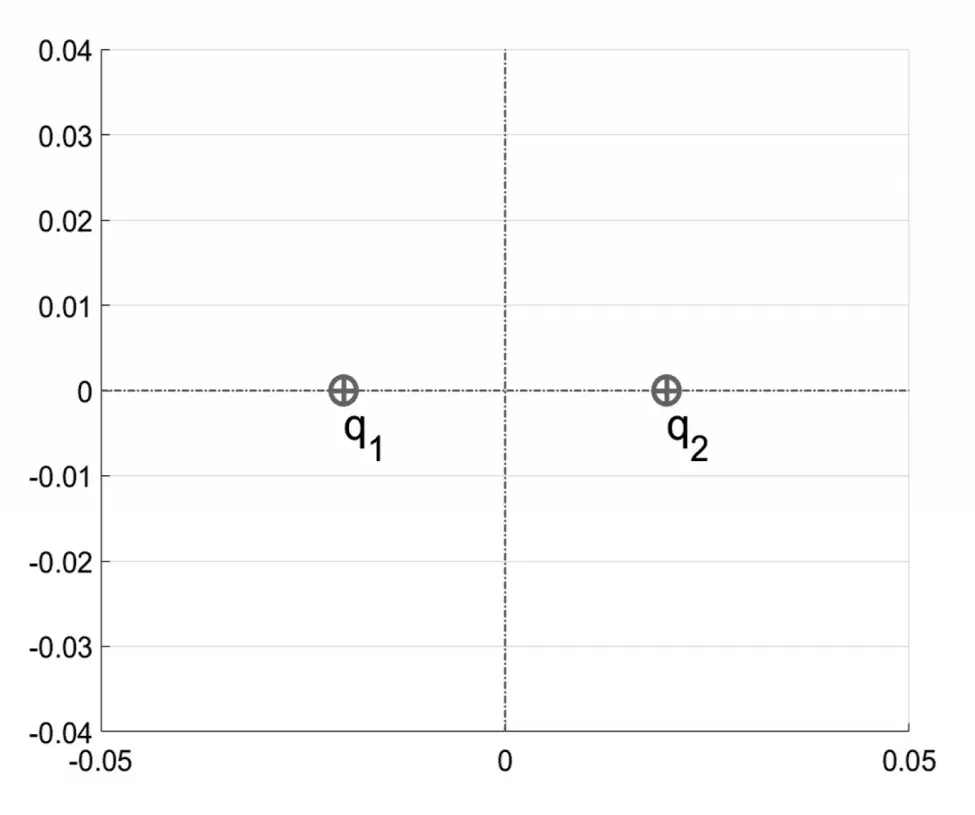
图3

在左电荷q1圆的表面等分取12 个点，取一个点出发求电场线。利用点电荷公式E=，获得左右电荷q1与q2各自在这个点上产生的场强的大小和方向，利用场叠加原理得到合场强。借助微元思想，沿着合场强的方向前进一个微小距离获得一个新点，重复以上计算。每1000 个点作图一次，利用quiver 函数绘制合场强与分场强，line 函数补绘平行四边形，展示出该处的场强叠加。作图完毕后，将合场强矢量归一化处理后保留。如图4、图5 所示：

图4

图5

最后用plot 函数将这些点连起来即可得到一条光滑的电场线。如图6 所示：

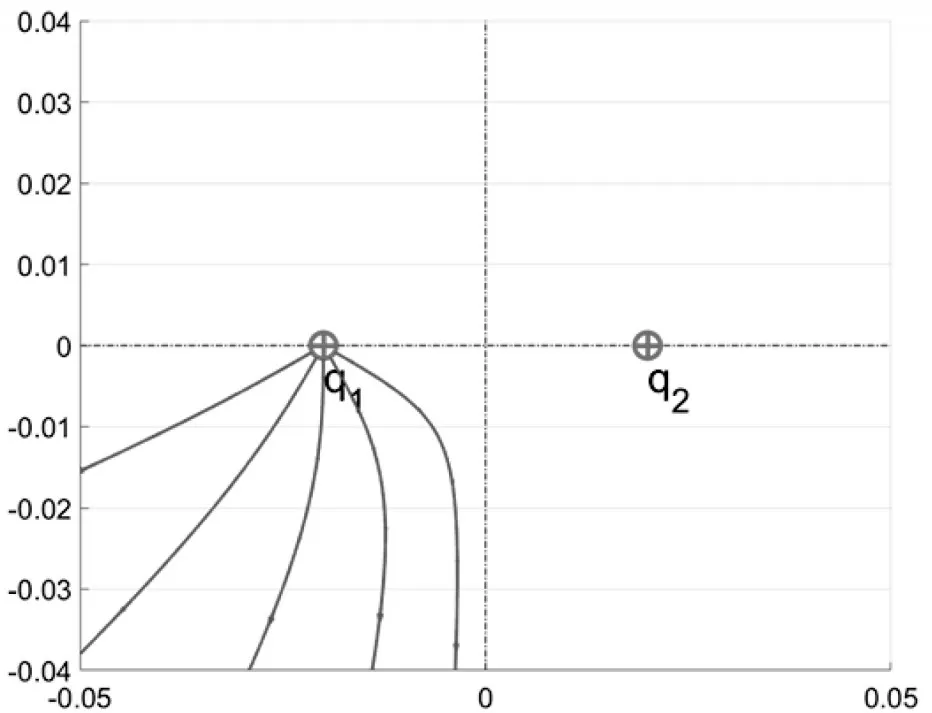
图6

特别地，从作图过程中可以清晰地观察到点电荷连线与中垂线上的场强叠加，如图7、图8 所示。通过循环语句，可以求出左半区间的12 条电场线，如图9所示。

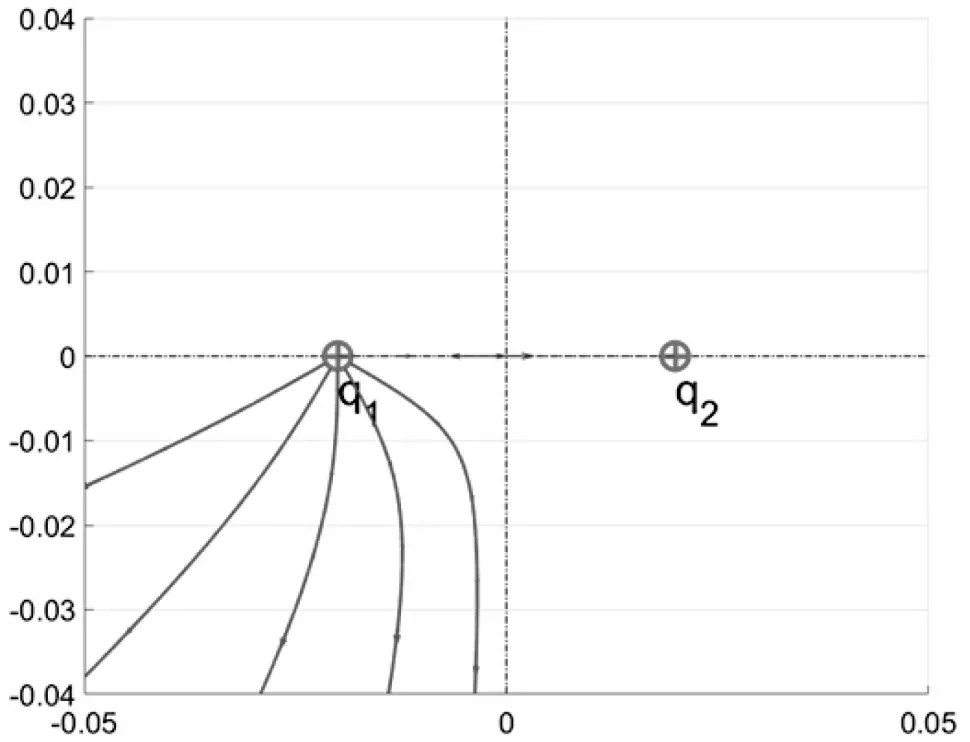
图7

图8

图9

同理也可求出右半区间的12 条电场线，如图10所示。然后利用contour 函数沿着电场线降落方向依次画出等势面（单位为V），基本的特征是电场线垂直等势面。如果对等势面标上电势，可以明确看到电场线由高电势指向低电势，如图11，图12 所示。

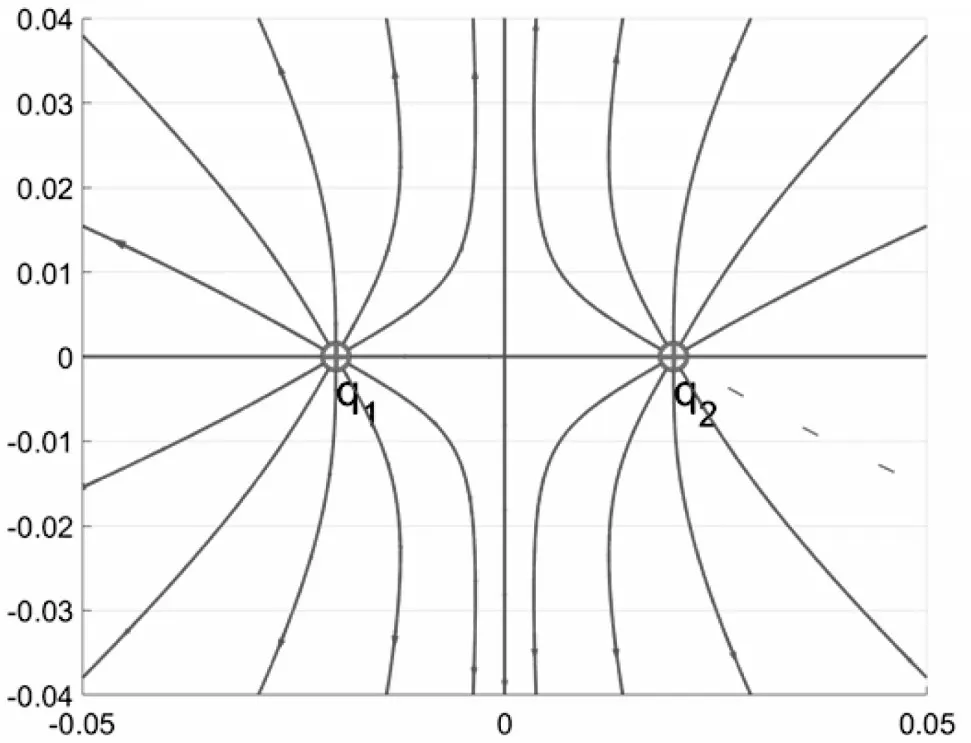
图10

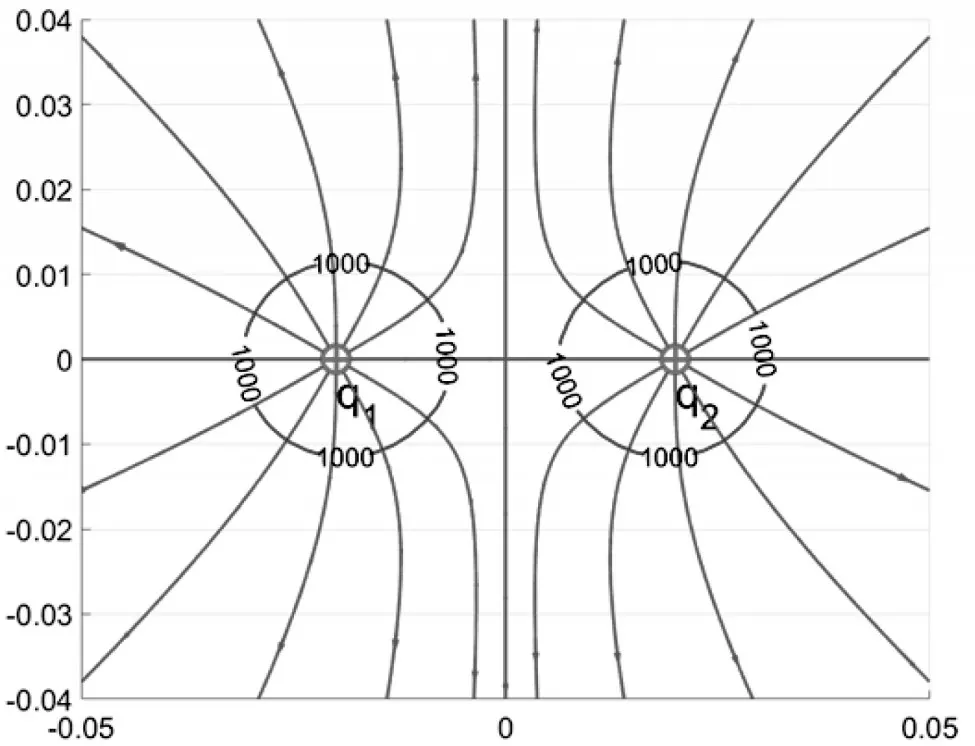
图11

图12

作为新手，学生可以观察到专家的电场概念模型是如何建构的。最后完整的电场模型如图13 所示。

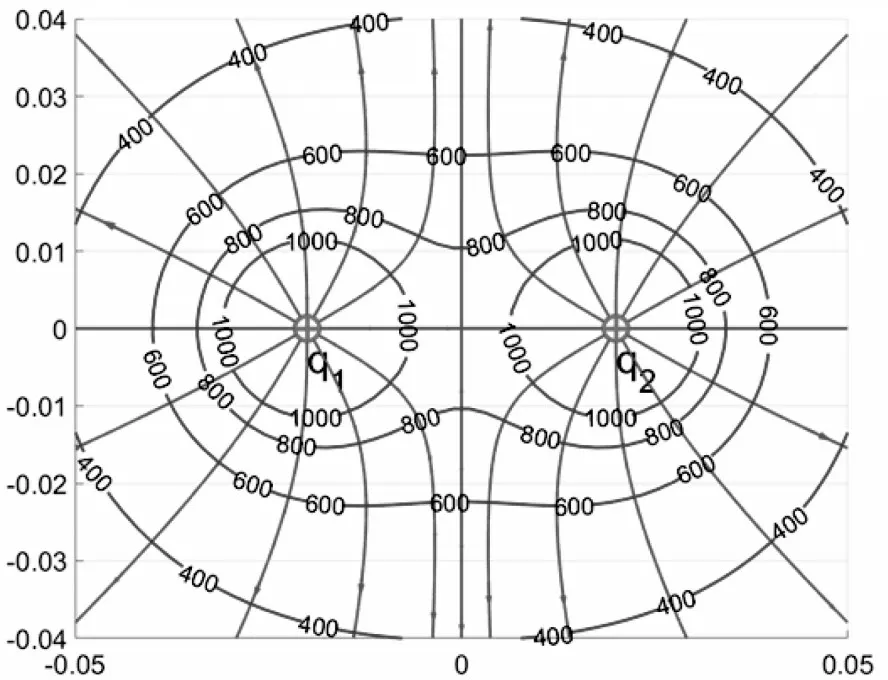
图13

（二）模型验证

当模型生成以后，引导学生利用数学表征Δφ=EΔx 分析图像，自然可以发现电场线密集的地方，等势面也密集。这就是数学表征Δφ=EΔx 的深刻含义。学生的概念发生了转变，完成了“静电场力的性质”“静电场能的性质”两个层级的整合。同时可以发现电场强度的大小与电势高低无关，迷思概念被纠正。

通过以上例子可以发现：计算机仿真可以将抽象的数学表征可视化，整个作图过程其实也就是相应的建模过程。在观察过程中，学生会更深刻地理解电场的数学表征，“静电场力的性质”“静电场能的性质”两个层级概念发生整合，升华成静电场的观念，从而建构起较为正确的心智模型。

（三）模型分析

此时可以指导学生分析中垂线上的场强情况。若q1，q2的距离为L，设中垂线上任意点和q1的连接线与q1，q2连线的张角为θ，引导学生应用场强叠加原理推导得E=cos2θ sin θ，可以定性地判断中垂线上场强变化规律应当是随着θ 的增加先增后减。

如果将绘图的区间扩大，可以观察到在中垂线附近区域，上下半区间电场线各有一处最为密集，直观地验证了这一点，如图14 所示。

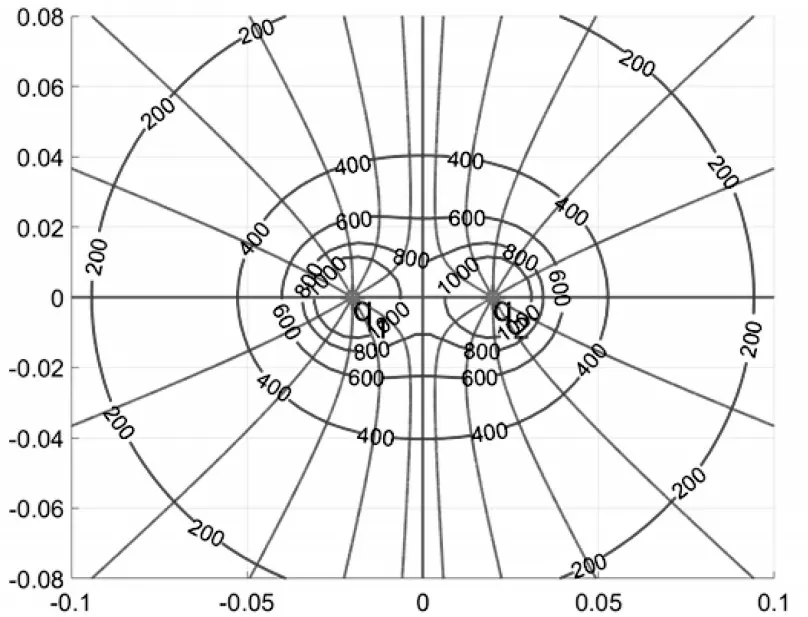
图14

（四）模型调度

我们甚至可以引导学生在此基础上进行延伸，分析不等量电荷的场强空间分布。先让学生思考分析判断分布情况，然后教师利用计算机仿真给出答案进行验证。

这样可以有效地帮助学生发展迁移的技巧。如图15 所示，q1的电量是q2的两倍，可见q1与q2连线上场强为0 的点在右半区间。（取q2=1×10-9C，坐标单位为m）

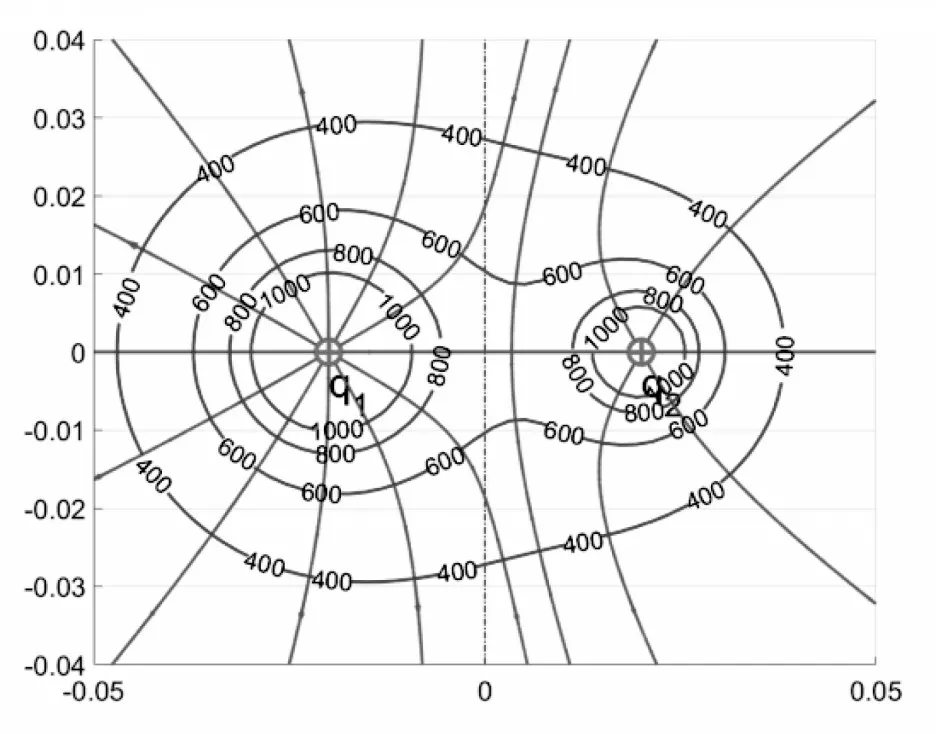
图15