基于光电跟踪的火炮轴线空间角测量方法

李国栋，张 勇，张 玺

（1.陆军工程大学军械士官学校，武汉 430075；2.中国人民解放军32181 部队，西安 710032）

为提升车载武器系统的机动性和精确打击能力，坦克、自行火炮等新型武器系统均将惯导设备直接安装在身管之上，精确输出身管的空间指向信息传递给火控系统，火控系统快速解算射击诸元，以减少传统安装形式带来的误差。此时要求惯导设备轴线与火炮身管轴线尽量一致，才能使惯导输出的高低角、方位角信息准确表征火炮轴线的空间指向。因此，在惯导设备安装和一段时间使用后需要对惯导设备轴线与火炮身管轴线空间指向的一致性进行检查和标定。由于目前安装在火炮上的惯导设备轴线无法引出，检查和标定过程实际上是对火炮身管轴线空间指向的精确测量，根据测量结果评估惯导设备测量误差，若误差过大，可通过火炮终端对惯导设备安装误差进行修正。

对火炮身管轴线空间指向的测量，传统的方法有双站经纬仪法[1-4]、陀螺测量、全站仪测量、卫星测姿[5]、视觉测量、激光跟踪仪法[6]等。但在应用场景、测量精度、测量效率或性价比方面不同程度存在一定局限性。

为了实现精度高、实时性好、性价比高的测量系统，本文提出综合利用光电跟踪[7-9]和北斗定向[10]快速测定火炮身管轴线空间指向的方法。该方法将相位激光测距机与高分辨率相机安装在高精度双轴伺服机构上，将北斗定向双天线安装在目标靶板和伺服机构上，利用北斗定向双天线获取被测对象的初始空间角，利用相位激光测距获得被测对象与目标靶板之间的空间距离，利用高分辨率相机与高精度伺服机构实时跟踪目标靶板，采集被测对象相对于目标靶板的空间角度信息，通过实时空间解算获取火炮身管轴线的空间角。

1 基于光电跟踪的火炮身管空间角测量方法

1.1 火炮空间角测量系统

火炮空间角测量系统由测量装置和目标靶板两部分组成。被测火炮停放在平坦地面上，测量装置插入火炮身管前端，身管夹持引出机构与火炮身管内壁紧密贴合，保证身管轴线精确引出到测量装置上。身管夹持引出机构与高精度双轴伺服机构固连，相位激光测距机和高分辨率相机安装在高精度双轴伺服机构上，高精度双轴伺服机构上方安装一只北斗天线。目标靶板架设在火炮正前方30～50 米远的位置，靶板正上方安装另一只北斗天线。高精度双轴伺服机构可带动测距机和相机实现方位和高低转动，为外方位内俯仰结构，由力矩电机驱动，旋转变压器实现转动角度输出，其俯仰轴上安装有水准气泡。整个测量装置在加工安装过程中保证火炮身管轴线与身管夹持引出机构轴线共线，身管夹持引出机构轴线通过高精度双轴伺服机构回转中心，相机的CCD 中心与高精度双轴伺服机构回转中心重合，水准气泡可以标识伺服机构俯仰轴是否水平。

在测量安装过程中，将火炮身管调整到大致水平，插入测量装置，观察水平气泡居中，此时认为伺服机构俯仰轴水平，利用水平仪测量火炮横轴的倾斜角度，并记为γ。伺服机构调整方位和俯仰到零位，调整火炮身管指向，利用相机瞄准目标靶板十字中心，利用测距机测量伺服机构回转中心到目标靶板的空间距离，利用北斗双天线获取炮口到目标靶板的方位角和高低角，计算机进行初始空间角解算。火炮进行调炮操作，伺服机构带动相机跟踪目标靶板十字中心，计算机根据伺服机构输出的双轴转角实时解算火炮身管轴线的空间角。火炮空间角测量系统示意如图1 所示。

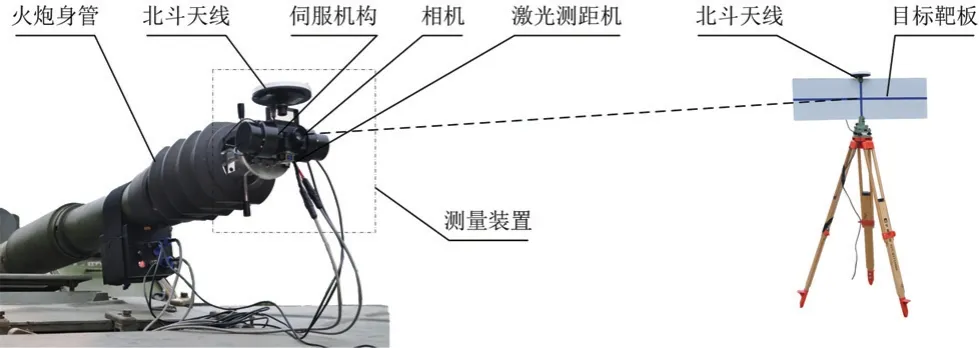
图1 火炮空间角测量系统示意图Fig.1 Schematic diagram of gun space angle measurement system

1.2 空间角解算

在对火炮身管实施光电跟踪测量过程中，分为两个状态，一是火炮处于大致水平状态，称为初始状态，此时可以利用北斗双天线测量出火炮身管的空间指向；二是火炮调炮到任意角度时的状态，称为任意调炮状态，此时利用伺服机构输出来解算火炮身管空间指向。在此两种状态下建立相关空间坐标系如图2 所示。

图2 空间坐标系示意图Fig.2 Schematic diagram of spatial coordinate system

火炮在初始状态下，身管轴线与相机瞄准线共线，并指向目标靶板中心，建立初始坐标系O-X bY b Zb，O为火炮回转中心，Yb轴沿身管轴线指向前；Xb轴沿火炮横轴指向右；Zb轴垂直于Xb与Yb指向天顶方向。火炮回转中心到目标靶板中心的矢量在初始坐标系下表示为：

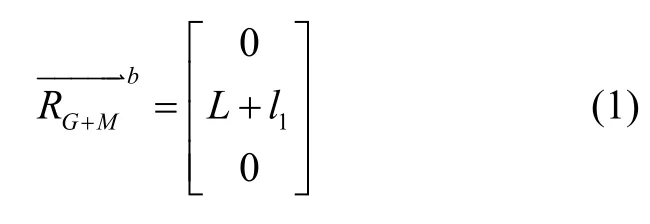
式中L为火炮回转中心到伺服机构回转中心的距离，l1为伺服机构回转中心到目标靶板中心的距离。

火炮在任意调炮状态下，方向转动α，俯仰转动β，此时建立身管坐标系O-X g Yg Zg，O为火炮回转中心，Yg轴沿身管轴线指向前；Xg轴沿火炮横轴指向右；Zg轴垂直于Xg与Yg指向天顶方向。火炮回转中心到伺服机构回转中心的矢量在身管坐标系下表示为：

火炮调炮过程中，伺服机构控制相机跟踪目标靶板十字中心，首先建立相机坐标系Om-X m Ym Zm，Om为相机中心，也即伺服机构回转中心，Y m为相机光轴指向目标靶板中心，Xm沿伺服机构俯仰轴指向右，Zm垂直于Xm与Ym指向上。伺服机构回转中心到目标靶板中心的矢量在相机坐标系下表示为：

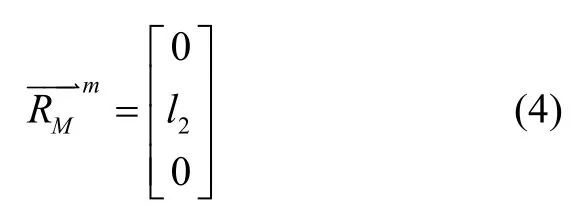
式中l2为伺服机构回转中心到目标靶板中心的距离。

建立伺服机构坐标系Os-X s Ys Zs，O s为伺服机构回转中心，Ys沿身管轴线指向前，Xs垂直于Ys指向右，与火炮横轴相差γ角，Zs垂直于Xs和Ys指向上。伺服机构控制相机跟踪目标靶板十字中心，方位输出α1，高低输出β1，则伺服机构回转中心到目标靶板中心的矢量在伺服机构坐标系下表示为：

该矢量在身管坐标系下表示为：

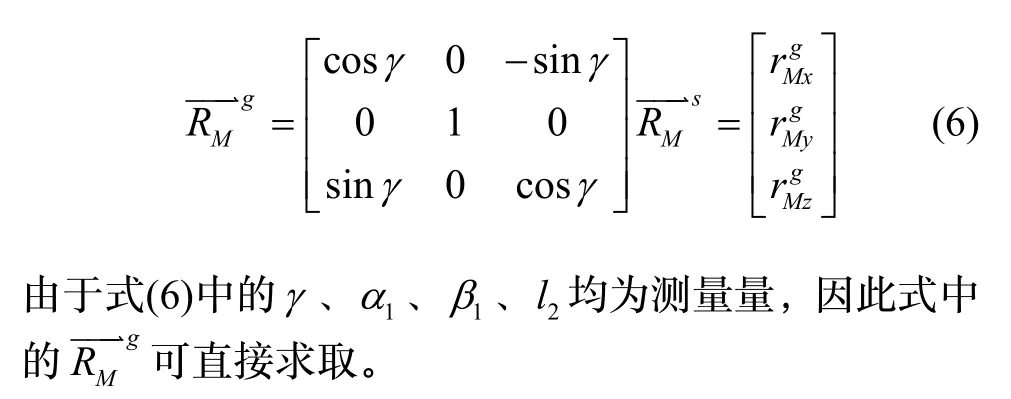
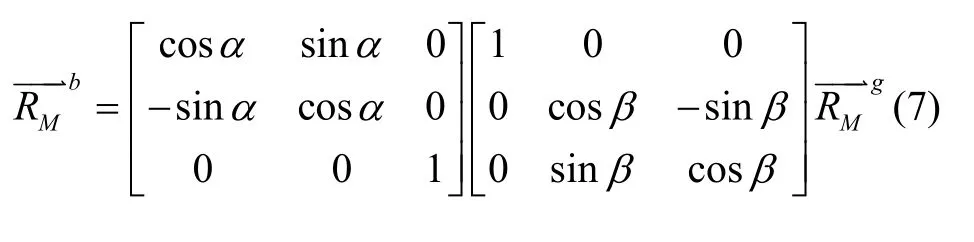
同理，该矢量在初始坐标系下表示为：

根据上述矢量关系可列矢量方程为：

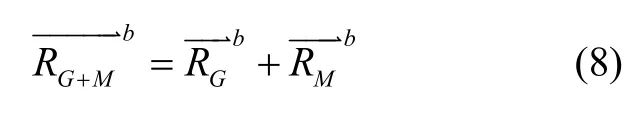
将式(1)(2)(3)(6)(7)代入式(8)，得：

根据式(10)可解得：

可得火炮身管在初始坐标系下的矢量为：

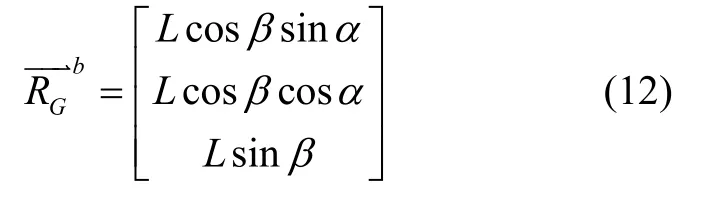
初始坐标系的方位角αt和高低角βt，在初始状态下可利用北斗双天线获取，横倾角为γ。由于在初始状态下，火炮身管轴线和横轴基本处于水平，其βt和γ两角很小，可以近似认为初始坐标系经过以下三次旋转变换到地理坐标系下：先绕Yb轴转γ角，再绕Xb轴转βt角，最后绕Zb轴转αt角到地理坐标系。火炮身管在地理坐标系下的单位矢量为：

则火炮身管轴线的空间角为：

2 火炮空间角测量系统误差分析

根据火炮空间角测量系统各测量单元的结构可知，其测量误差的来源包括共轴误差、北斗测量误差、相机瞄准误差、测距误差、伺服机构误差、横倾角测量误差。

2.1 共轴误差

共轴误差σ1分为两种情况，一是相机和伺服机构框架的共轴误差，二是身管夹持引出机构与被测对象之间的共轴误差。针对第一种情况，通过安装调试可将误差控制在10″以内；针对第二种情况，采用四点贴合身管内壁精密加工和弹簧顶块锁紧方式，可将机构引出轴线与身管轴线的共轴误差控制在8″以内。由于两种情况误差相互独立，则

2.2 北斗测量误差

北斗测量误差包括定向误差和高低角误差。北斗双天线定向设备的定向精度标称值为0.1°/m，通过将该设备放置在50 m 长的标准基线上进行测试，其定向精度为10″/50 m（1σ），满足正态分布。当基线长度为30 米时，其定向误差σα为15″，高低角误差按定向误差的2 倍计算，σβ为30″。

2.3 相机瞄准误差

相机瞄准误差主要指相机的电十字分划与目标靶板十字分划之间的瞄准偏差，由相机的角分辨率决定。采用高分辨率相机的像元尺寸为4.8 μm，焦距为75 mm，则相机瞄准误差σm为：

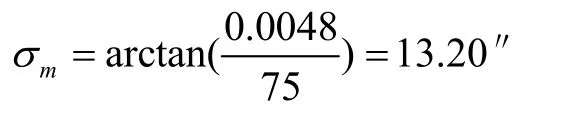
2.4 测距误差

测距误差是激光测距机测量伺服机构回转中心到目标靶板中心距离的误差，采用相位激光测距机，其测距误差σd为2 mm，满足正态分布。

2.5 伺服机构误差

伺服机构采用位置、速度双回路反馈控制方案，控制精度为14.4″；数据传输分辨率为3.6″；选用正余弦旋转变压器重复性指标为2.4″。伺服机构转角测量误差为：

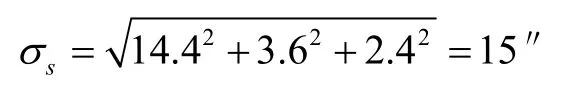
2.6 横倾角测量误差

横倾角测量误差主要来源于两个方面，一方面是电子水平仪测量火炮横轴产生的误差，采用高精度电子水平仪测量，误差可控制在2″以内；另一方面来源于测量装置安装于身管时观察水准气泡的误差，水准气泡的指示精度为20″/2 mm，测量装置横倾安装精度可控制在10″以内。综合以上，横倾角测量误差为：

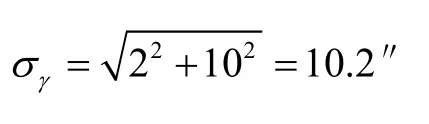
3 测量系统蒙特卡洛仿真分析

根据蒙特卡洛仿真分析方法，在给定输入量上叠加满足一定规律的误差量，代入空间解算模型，得到某一空间角数值，然后与空间角的真值进行比对得到空间角的误差值，通过数万次的反复计算，对得到的误差值进行统计分析即可获得系统误差规律。

3.1 输入输出量分析

该系统的输入量为αt、βt、γ、L、l1、l2、α1、β1，中间量为α、β，输出量为αGt、βGt。

从系统工作原理和空间解算模型来看，系统误差的产生主要跟测量系统有关，与火炮停放的绝对方位无关，因此，在进行仿真分析时，只要任取一组初始状态的αt、βt即可。仿真分析应主要集中在其它输入量与中间量的误差变化规律上。

只要火炮与目标靶板位置不变，对于输入量L、l1是固定值，无论火炮调炮到任何角度，L、l1均不变，因此，仿真分析时给定适当的常值即可。

输入量γ表征了火炮停放好后的横倾状态，测量条件要求γ不能太大，实际情况一般不大于3°，因此在仿真时给出3°即可。

输入量l2、α1、β1是火炮在任意角度调炮状态下由测量系统给出的测量值，不可任意给定，受其它输入量和中间量α、β的约束，因此应根据其它输入量和中间量给定值计算出输入量l2、α1、β1的值。根据空间解算模型，以下矩阵记为：

式(8)的矢量方程可列写为：

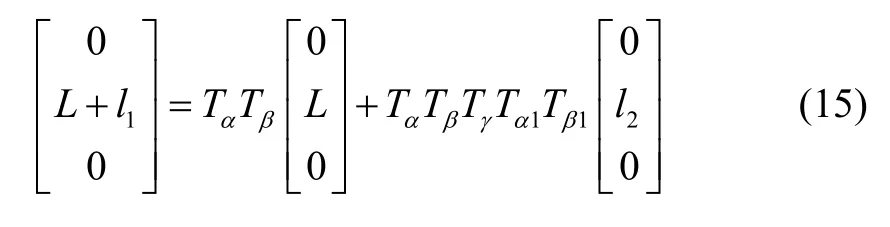
整理式(15)并记为：

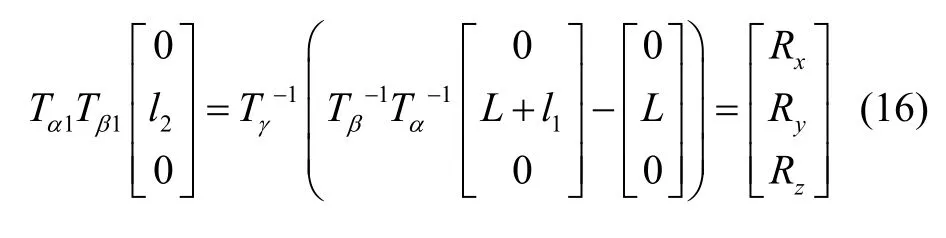
由于输入量γ、L、l1和中间量α、β已给定，可根据式(16)得到：

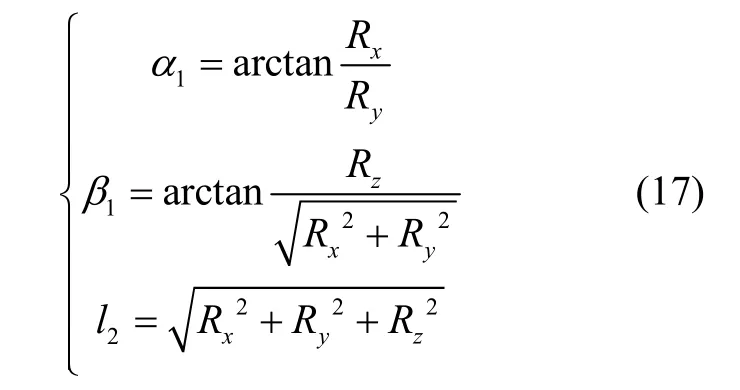
3.2 蒙特卡洛仿真分析步骤

第一步，设定非约束输入量的取值与误差。根据测量实际情况，火炮停放方位任意，高低大致水平，给定αt=25°，βt=-2°，αt、βt误差分别满足N(0，1 5″)，N(0,30″)；L=4.205 m 为固定值；l1=30 m，误差满足N(0,2 mm)；γ的取值范围为3 °，误差满足N(0,10.2″)。

第二步，设定中间量的取值α、β。根据一般操作情况，α的取值范围为-25 °～25 °，从-25 °开始，间隔步长为5 °；β的取值范围为-30 °～30 °，从-30 °开始，间隔步长为10 °。

第三步，计算约束输入量的取值与误差。根据上述给定取值，按照式(17)计算l2、α1、β1的对应值，l2误差满足N(0,2 mm)，α1、β1的误差主要由相机瞄准误差和伺服机构误差引起，满足N(0,19.98″)。

第四步，仿真计算。利用相应误差分布规律的随机函数产生误差值，分别加到输入量上，然后代入公式(11)等，计算得到α、β，再代入式(14)，计算得到αGt、βGt。利用预先设定的α、β代入式(14)，计算得到αGt、βGt，两次得到的αGt、βGt做差，即为输出量的仿真误差量。对该步骤重复5～10 万次，可获取大量的误差量，对误差量求取标准差。

第五步，按照第一、二步规定的取值和步长，分别对不同的α、β进行取值，可获得不同角度状态的仿真结果，并对整体结果进行分析，得出结论。

3.3 蒙特卡洛仿真结果

在火炮横倾角3°的条件下，分别取火炮方位调炮范围-25°～25°、高低调炮范围为-30°～30°的不同值进行蒙特卡洛仿真，得到的测量误差如图3 所示。对77组误差值取标准差，得到测量系统的测量误差为51.26秒。由于蒙特卡洛仿真未考虑共轴误差影响，在上述仿真结果的基础上综合共轴误差，系统总体误差为：

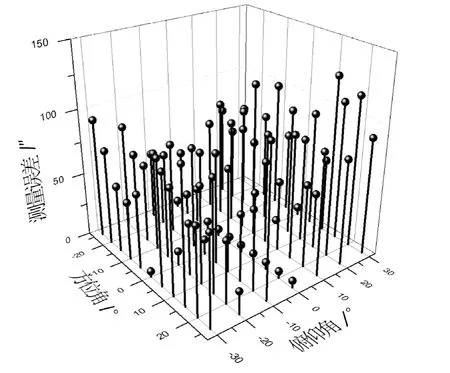
图3 任意角度测量误差图Fig.3 Error diagram of arbitrary angle measurement

4 实验验证

利用传统双站经纬仪方法和本文方法对火炮身管空间角进行测量对比实验，分别从测量精度和测量效率两方面进行对比。

4.1 测量精度实验

操作火炮调炮到不同位置，同时利用本文方法和双站经纬仪方法对身管空间指向进行测量，其中双站经纬仪方法的测量精度为0.2 mil。测量结果如表1。

表1 对比实验结果Tab.1 Comparative experimental results

上述测量数据，方位测量差值的平均值为0.05 mil，高低测量差值的平均值为0.01 mil，方位测量差值的标准差为0.24 mil=51.84″，与测量系统蒙特卡洛分析结果相当，高低测量差值的标准差为0.21 mil。实验结果表明：利用本文测量方法对火炮身管空间指向的测量精度与双站经纬仪测量方法基本相当，精度可满足火炮身管空间角的测量需求。

4.2 操作效率实验

火炮停放室外开阔位置，利用本文的空间角测量系统对火炮4 个调炮位置进行测量，从测量系统安装开始计时，到完成测量计时结束，共计用时43 min。利用双站经纬仪方法对火炮4 个调炮位置进行测量，从经纬仪架设整置开始计时，经历北斗定向，瞄准线穿膛、引北、双站测量等操作过程，到完成测量共计用时132 分钟。由此可见，本文方法的测量效率较双站经纬仪方法提高3 倍左右。

5 结论

本文介绍了基于光电跟踪的火炮轴线空间角测量系统，建立空间角测量解算模型，并对系统进行了相关的误差分析，同时利用蒙特卡洛仿真方法对测量系统的误差规律进行了仿真分析。从仿真分析结果来看，该系统对火炮身管轴线空间角的测量精度优于0.25 mil。利用本文方法和双站经纬仪测量方法对某火炮进行了对比实验，实验结果表明：本文方法对火炮身管空间角测量精度与双站经纬仪方法测量精度基本相当，测量效率明显提高，是双站经纬仪方法测量效率的3 倍左右。