基于虚拟圆球法向量位置模型的航海惯导全球容错阻尼算法

冯国虎，吴文启，曾观林

（国防科技大学 智能科学学院，长沙 410073）

对于航海导航，长航时导航精度和可靠性至关重要。惯性导航具有连续性好、自主性高、隐蔽性强的特点，是航海组合导航的重要基础[1]。受水下环境限制，组合导航主要依赖惯导/计程仪组合。基于速度观测的组合导航精度依赖于计程仪速度精度。当舰船在深远海航行时，计程仪信号无法到达海底，此时计程仪测量的是对水速度而不是对地速度。由于洋流速度难以准确建模和实时测量，计程仪测速精度受限，基于速度观测的滤波算法精度受计程仪测速精度影响大，而阻尼技术在载体匀速直航条件下可以做到高阶无静差，受计程仪测速精度影响小，因此阻尼技术成为主要手段[2,3]。然而，当计程仪测速误差变化剧烈时，阻尼算法效果也不好。为确保导航可靠性，需切断舒勒回路的阻尼，由阻尼状态变成无阻尼状态，以保持惯导导航精度。等计程仪测速误差变化平缓后，再由无阻尼切换到阻尼。变阻尼瞬间舒勒回路容易出现大幅超调振荡，影响阻尼效果[4,5]。

变阻尼是阻尼算法的研究重点[6]。传统阻尼基于反馈校正实现，破坏了纯惯导解算过程，阻尼切换不当会引起较大的导航误差。本文针对传统阻尼算法的不足，基于虚拟圆球法向量位置模型设计了容错阻尼算法。相对传统阻尼算法，本文算法同时具备惯导两套解算结果：一套阻尼，一套无阻尼。无阻尼解算不受阻尼影响。基于北极科考导航数据的仿真验证表明，本文算法的阻尼效果与传统阻尼算法相当，在阻尼切换方面，定位精度更高。

1 基于法向量位置模型的误差微分方程

传统的惯性导航阻尼不适用于极区。当舰船出入极区时，需要将传统导航算法与极区算法进行切换，切换过程会影响阻尼内部过程的连续性与一致性[7,8]，因此在全球统一的机械编排下实现阻尼算法十分必要。本文在全球适用的法向量位置模型下设计实现阻尼。

文献[9]对法向量位置模型的建立和法向量的位置表示方法进行了详细推导。如图1 所示，由载体对应参考椭球位置的卯酉圈构造一个虚拟圆球，其球心为对应卯酉圈的圆心，圆球半径为卯酉圈半径ER与大地高度h之和。

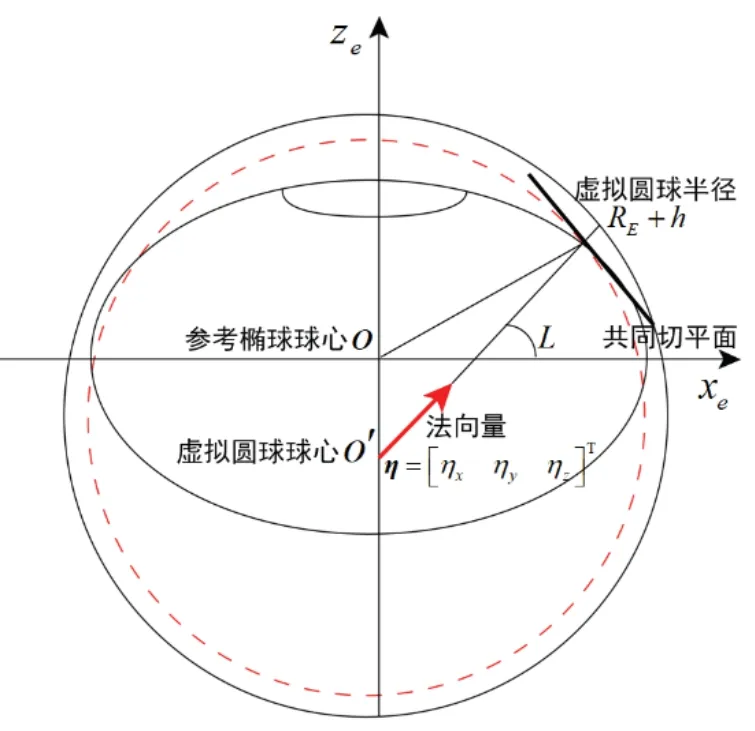
图1 虚拟圆球法向量示意图Fig.1 Sketch of virtual sphere n-vector

法向量η=是虚拟圆球球心指向载体位置的单位矢量，是当地水平面法向量在地球坐标系下的投影，用来表征载体的水平位置。大地高度h即载体位置相对地球椭球模型表面的高程，表征载体的垂直位置。在此模型下，用包含法向量的四元组代替经纬高表示载体位置，避免了位置表示的奇异性问题。基于法向量位置模型的惯性导航机械编排方案形式更简洁、实现更简便并且适用于全球。

水平通道的姿态、速度以及位置误差微分方程式为[9]：

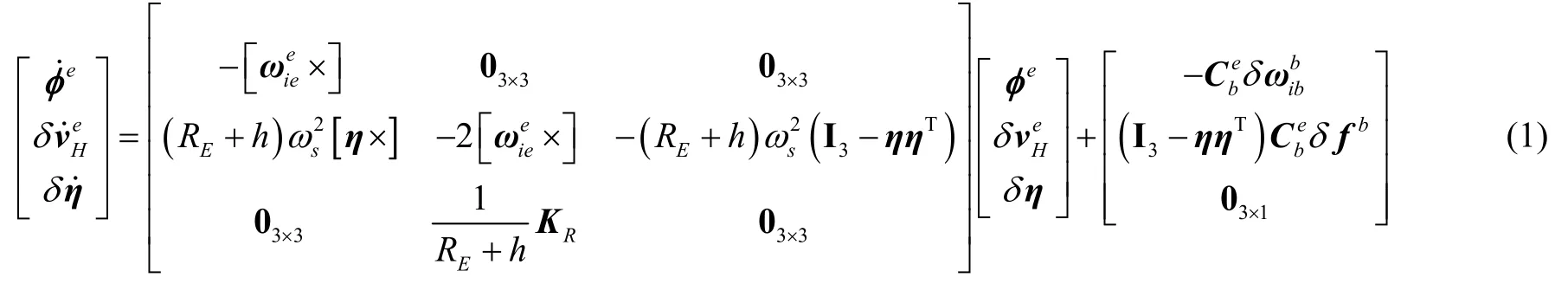
其中，φe为姿态角误差矢量，为水平速度误差矢量，δη为法向量误差矢量,为角速度误差矢量。

纯惯导系统的垂直通道不稳定，需要对垂直通道进行阻尼。在静基座的垂直通道中引入参考高度进行反馈补偿,使系统闭环稳定从而抑制高度发散。可以得到经过阻尼后垂直通道的高度和速度的误差微分方程为[10]：

式中uD1与uD2是引入的反馈，即：

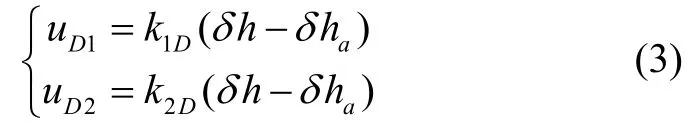
其中，k1D与k2D为反馈系数。由于计深仪测量高度ha=htrue+δha，导航计算高度h=htrue+δh，因此δ h-δha等价于计算高度与参考高度之差h-ha。

2 容错阻尼算法

容错阻尼算法框图如图2 所示，有两套惯导解算，一套用于无阻尼纯惯导解算，另一套用于阻尼惯导解算。无阻尼纯惯导解算，输入是三个加速度计、三个陀螺仪采样值，输出是惯导解算的速度、位置和姿态。阻尼惯导解算过程中，输入是纯惯导解算的速度、位置和反馈的阻尼速度、位置，输出是与纯惯导解算频率一致的速度、高度。输出的速度、高度与外部参考速度、高度一并输入阻尼惯导解算中阻尼环节，高度阻尼环节输出阻尼高度，速度阻尼环节输出阻尼速度和法向量，法向量和阻尼高度合成阻尼位置。

图2 容错阻尼算法框图Fig.2 Block diagram of fault tolerant damping method

阻尼位置合成公式为：

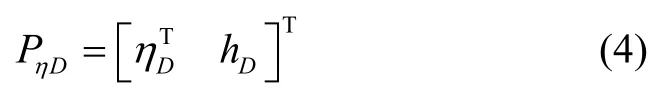
式中下标D是阻尼damp 的缩写。

容错阻尼算法中的阻尼环节与传统阻尼算法[10]相同，不同的是，容错阻尼算法有惯导两套解算，其中纯惯导解算不受阻尼惯导解算影响。当外参考速度误差变化剧烈，需要由阻尼切换至无阻尼时，可以使用纯惯导解算结果。待外参考速度误差变化平缓，由无阻尼切换至阻尼。

容错阻尼算法的两个特点：1.同时具备纯惯导解算和阻尼惯导解算，阻尼切换方便，避免了阻尼切换过程引起的超调振荡。2.阻尼惯导解算在纯惯导解算外部完成，阻尼惯导解算过程以及结果不影响纯惯导解算，增强了可靠性。

2.1 速度阻尼

相对惯导解算频率，提供外参考速度的计程仪解算频率较低。

有外参考速度时，阻尼速度微分方程：

式中，C是速度阻尼函数。

无阻尼纯惯导解算的速度微分方程：

由于阻尼惯导解算与无阻尼纯惯导解算测量同一载体运动，即两者公式中比力项相同。阻尼速度微分方程减去无阻尼速度微分方程，得：

选取Q为相位滞后-超前串联校正网络[10]：

式中ε为阻尼比，ωs为舒勒周期频率，该校正网络的位置稳态误差是三阶无静差。

没有外参考速度时，阻尼速度按纯惯导解算频率更新：

阻尼速度微分方程减去无阻尼速度微分方程，得：

方程两边积分，得：

采取迭代法求阻尼速度。具体步骤如下：

阻尼速度初始值计算：

阻尼位置初始值计算：

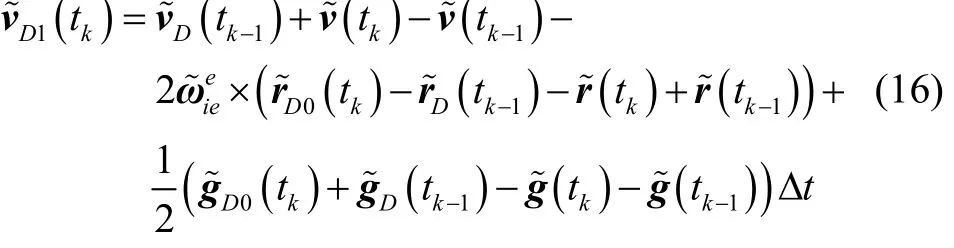
阻尼位置更新值：

2.2 阻尼切换

计程仪测速精度受使用环境限制，一方面测速数据会被环绕载体的畸变水流污染；另一方面载体运动状态发生改变或某些海域的洋流大小和方向变化明显，会使得外参考速度误差变化非常快。而当由洋流或者载体机动引起的外参考速度误差超差时，阻尼有可能引起较大的导航参数误差，应当切换到无阻尼模式。

为了判定外参考速度信息是否可用，设置外速度误差变化判据G(k) ：

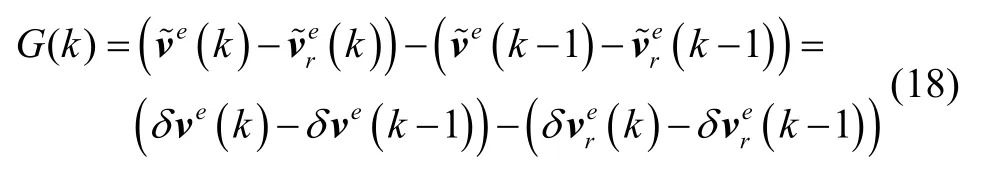
式中，δve（k）-δve（k-1）为k和k-1 时刻惯性系统速度误差的差值，由于惯导系统解算具有连续性，因此相临时刻惯导速度误差的差值可以忽略。为k和k-1 时刻计程仪速度误差的差值，如果G(k) 的模较大，超过设定阈值（可以选取计程仪测速误差最大值的2 倍作为阈值，也可以根据舰艇航行的实际情况，制定适当的标准作为阈值），则可以认为外参考速度误差变化剧烈，阻尼状态自动切换至无阻尼状态。待G(k) 的模小于阈值，无阻尼状态自动切换至阻尼状态。

高度阻尼和垂直速度计算与文献[10]相同，不再赘述。

3 基于实测数据的仿真验证

采用北极科学考察的船载导航数据对容错阻尼算法进行仿真验证，并与纯惯导和传统外速度阻尼算法进行比较。运动轨迹如图3 所示，数据采用GNSS 数据作为参考真值，从起始位置(56.99 °N,174.1 °E)开始，经过72小时穿越180°经线运动至71.37 °N,169.5 °W)。

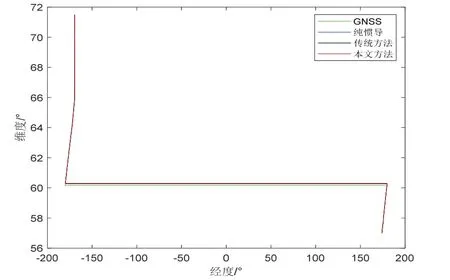
图3 航行轨迹及解算轨迹Fig.3 Trajectory curves of different method

垂直通道阻尼效果与文献[10]相同，本文主要展示水平通道的速度阻尼效果。

3.1 速度阻尼验证

速度曲线如图4 所示，相对纯惯导解算，本文方法可以抑制舒勒周期振荡误差。本文方法与传统方法效果相当。

图4 阻尼前后格网速度曲线Fig.4 Damped and undamped grid velocity curves

以纯惯导定位误差最大值为1 进行归一化处理，位置误差归一化曲线如图5 所示，相对纯惯导定位误差，本文方法可以抑制周期振荡误差，提高惯导系统定位精度。比较本文方法和传统阻尼方法的位置误差曲线，两者精度相当。

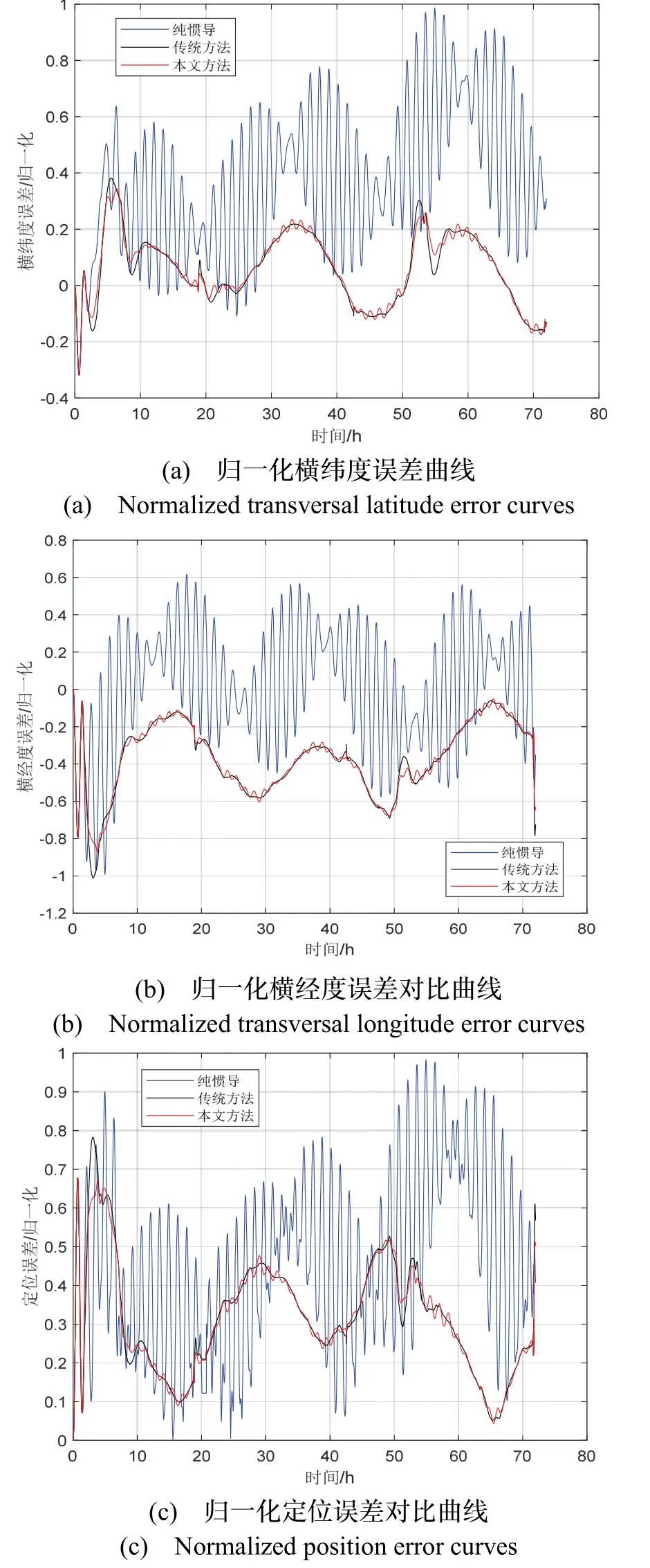
图5 阻尼前后归一化位置误差曲线Fig.5 Damped and undamped normalized position error curves

传统阻尼方法基于反馈校正实现，本文容错阻尼算法基于输出校正实现。理论上，输出校正与反馈校正精度相同。本文容错阻尼算法输入是纯惯导解算结果，阻尼速度计算采用迭代法近似，存在时间延误等因素影响，定位误差比传统阻尼方法大。从定位误差曲线来看，本文方法和传统方法精度相当。虽然精度上付出了些许代价，带来的好处是增强了算法的工程适应性，因为在实际使用中，受通信资源所限，不一定能获得惯导的加速度计、陀螺仪原始采样值。

3.2 阻尼切换验证

在29.5～31 h 内计程仪速度由于加入斜坡振荡干扰，先幅值增大，然后等幅振荡，最后幅值减小。计程仪速度精度超差时，系统由阻尼状态切换至无阻尼纯惯导解算，计程仪速度精度恢复正常后，系统由无阻尼切换至阻尼状态。

系统由阻尼切换至无阻尼状态，传统方法切换为纯惯导解算，本文方法中将阻尼惯导的计程仪速度替换为纯惯导速度实现等效的无阻尼纯惯导运算。

斜坡振荡幅值设置不同数值，振幅大、中、小三种情况对应的阻尼方法归一化定位误差曲线如图6 所示。相同阈值切换条件下，计程仪速度中斜坡振荡干扰增大快时，根据阈值切换条件判断，会较早发现计程仪速度超差，较早进行阻尼切换；而当计程仪速度中斜坡振荡干扰增大较慢时，根据阈值切换条件判断，则会较晚发现计程仪速度超差，较晚进行阻尼切换，因此图6 的三种情况中，定位误差曲线受计程仪速度中斜坡振荡幅值影响的情况相似。

图6 不同振荡幅值的归一化定位误差曲线Fig.6 Normalized position error curves at different oscillation amplitudes

计程仪速度中出现干扰，如果阻尼切换存在较大延迟，传统方法定位误差受计程仪速度误差干扰的影响较大，如图7 所示。比较图6 和图7 发现，无阻尼切换阻尼后刚开始一段时间内，传统方法定位误差曲线存在明显振荡，与文献[11]阻尼切换振荡现象相同，本文方法不存在明显振荡。

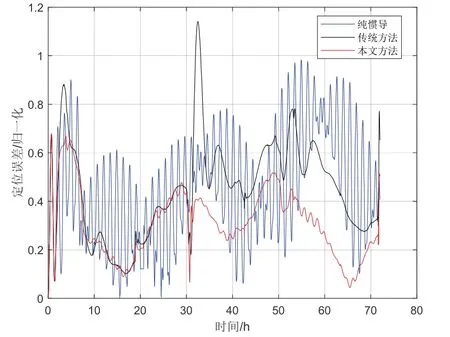
图7 阻尼切换延迟的归一化定位误差曲线Fig.7 Normalized position error of damping switching delay

比较图5(c)、图6 和图7 发现，相对于全程阻尼，无阻尼切换阻尼后的定位误差曲线，传统方法的曲线形状变化较大，本文方法的曲线形状变化较小，受阻尼切换影响较小。

设置计程仪速度中斜坡振荡干扰不同幅值进行测试，31 小时后传统方法和本文方法的误差数据如表1所示，相对传统方法，本文方法的归一化定位误差最大值和均方根更小。

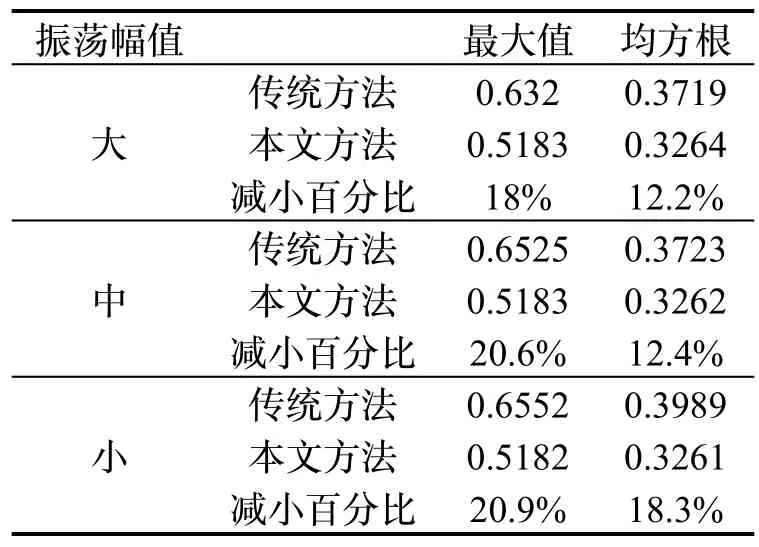
表1 计程仪速度中斜坡振荡干扰不同幅值的阻尼误差Tab.1 Damping error of different amplitude of slope oscillation in DVL velocity

综上所述，不需要阻尼切换时，本文方法与传统方位在定位精度上相当。需要阻尼切换时，本文方法比传统方法定位精度高。

4 结论

针对传统阻尼方法在无阻尼切换阻尼后定位误差超调振荡的不足，本文提出基于虚拟圆球法向量位置模型的航海惯导全球容错阻尼算法，同时具备无阻尼纯惯导解算和阻尼惯导解算。外参考速度精度超差时，阻尼惯导的外参考速度替换为纯惯导速度实现等效的无阻尼纯惯导解算，克服了传统阻尼方法阻尼切换的不足。

北极科考航行导航数据验证了本文算法的有效性，表明本文算法适用于穿越对向子午线的场景，具有全球适用性。在无须阻尼切换时，阻尼效果上与传统算法相当，在阻尼切换方面相对传统方法具有优势，均方根减小超过12%。