转子叶片碰磨故障诊断的叶端定时方法*

2022-12-16 06:22吴淑明陈雪峰杨志勃

航空制造技术 2022年20期

吴淑明，陈雪峰，杨志勃

（西安交通大学，西安 710049）

航空发动机是现代工业皇冠上的明珠，也是飞机的“心脏”、动力之源，是国家安全的重要战略保障。航空发动机往往工作在极端环境下，如高速、高温及重载，这些极端因素的共同作用使得仅依靠航空发动机的设计和制造品质无法完全抑制事故的发生。航空发动机使用过程中，典型常见故障有稳定性故障、气路故障、振动故障、磨损故障、熄火故障、轴承故障、结构疲劳以及控制系统故障等[1]。其中磨损故障通常是指转子叶片与机匣的碰磨，该类碰磨通常是由转子不平衡、不对中以及叶片伸长等引起的[2]。现代航空发动机为提升压气机性能，将叶尖与机匣之间的间隙尽量缩小，导致碰磨的风险增大。而碰磨故障可能导致摩擦损伤、可磨损涂层的过度磨损以及叶尖泄露能量增加导致的效率损失等[3]，严重时可能引起轴承磨损、叶片断裂等严重航空事故。因此，为满足提升航空发动机安全性与降低维修成本的重大需求，开展航空发动机叶片的健康管理与状态监测研究意义重大。国内外学者针对碰磨故障展开了大量研究，Ahmad[4]综述了叶片机匣碰磨时对刚度、阻尼、转子加速度、反向涡动、热效应、库仑摩擦等参数的影响规律。Jacquet-richardet等[5]分别针对叶片机匣碰磨和转静子碰磨进行了文献综述，简介了现有碰磨数值模型和试验装备，并阐述了碰磨接触过程中的现象。Ma等[3]从碰磨建模方法、仿真研究、试验研究的动态响应3个方面对现有叶片机匣碰磨进行了综述。Torkhani等[6]分别针对变速状态下轻度、中度和重度碰磨开展了仿真和试验研究，分析了不同转速下水平振动和垂直振动规律。Xu等[7]建立了双转子系统的碰磨故障非线性动力学模型，得到了转子叶片与机匣碰磨状态下整体结构的动态响应特性。

叶端定时法是当前非接触式测量方法的研究热点。2014年，美国普惠（P&W）公司首席专家Volponi[8]在美国机械工程学会（ASME）汇刊上综述了航空发动机健康管理的过去、现状和未来，强调叶片测试的叶端定时技术是未来研究重点和难点。由罗·罗公司等多家航空公司和曼彻斯特大学等多所高等院校成立的PIWG组织（Propulsion Instrumentation Working Group）更是将叶端定时系统列为推进航空发动机安全的先进测量系统[9]。

叶端定时系统相对于应变片，具有非接触性测量的优势，且同时可以测量多级多个叶片的振动信息。但由于叶端定时系统采集的是到达时间数据，且采样率由传感器数目决定，从而导致数据通常存在高度欠采样的特性，因此如何根据叶片动力学建模推导其故障状态下的振动特征，并从欠采样的数据中提取叶片的振动信息，如频率、幅值和相位等，两相对比进而推断叶片的故障类型与故障程度是国内外学者的研究重点，目前尚没有针对碰磨故障的叶端定时检测方法及流程。

现有的叶盘建模方法有集中参数模型[10–12]、连续参数模型[10，13–14]和有限元模型。集中参数模型具有简单易求解的特性，可用于研究叶盘在碰磨状态下的统计特性，但该模型缺乏系统的建模方法，由于人为因素的限制而导致模拟精度不足。连续参数法多采用梁和板等连续模型[15]，精度介于集中参数法与有限元模型法之间，不满足工程设计的需求，多用于失谐振动机理的研究。有限元模型相对于上述两种模型具有最高的模拟精度，然而更真实的模型往往意味着更高的运算成本。由于叶端定时方法可以直接观测叶端振动特性，受其他部件振动干扰影响较小，因此本文采用集中参数模型进行叶盘建模。

国内外学者针对叶端定时高度欠采样信号特征提取开展了大量研究。2009年，瑞典乌普萨拉大学Stoica 等[16]提出了非均匀傅里叶变换，但是此方法在辨识高频成分时表现出不鲁棒性；肯特州立大学Ruf等[17]提出了一种最小均方谱分析方法，但是仅适用于低频振动信号重构； 2013年，法国什孔泰大学的Vercoutter等[18]提出了最小方差谱估计方法，该方法是非均匀信号处理Capon谱方法的一个分支，可以有效减少频谱中的干扰。针对叶片振动信号在频域稀疏的特性，可以通过稀疏表征理论来进行建模。经典的稀疏表征模型的正则项是0范数，其物理意义是信号中非0元素的个数，但l0约束问题为NP–难问题。为解决上述问题，可以采用l0约束的松弛形式l1约束问题（非0元素绝对值之和），松弛后的问题虽然可以得到全局最优解，但对信号的稀疏约束能力要比l0问题弱，因此为了增强模型的稀疏表征能力，学者们提出了一系列优化正则项。Candès[19]提出了增强稀疏分解方法，该方法通过在每一步迭代中对目标函数加入自适应加权项，实现了利用少量观测信号实现信号特征提取的功能。

本文首先分别针对单叶片和整级叶盘建立了动力学缩减模型，针对单叶片模型，采用单自由度弹簧振子模型，分析了其在碰磨故障状态下的叶尖位移动态响应，得到了单个叶片在碰磨状态下的瞬态与稳态响应。针对整级叶盘模型，构建了多自由度多叶片–轮盘耦合模型，推导了在碰磨故障状态下的各叶片的叶尖动态响应，揭示了单个或多个叶片故障对同级其他叶片叶尖动态响应的影响规律。然后对建模的非欠采样下的碰磨叶尖模拟位移信号进行频谱分析，得到整级叶盘碰磨状态下叶尖振动的频谱特征，通过增强稀疏分解进行特征提取；分析了碰磨状态下传感器之间以及叶片之间的叶端定时信号特征，从而提出碰磨的判别指标及诊断流程。

1 碰磨单叶片动力学建模

本节研究对象为单叶片模型，研究重点为碰磨故障状态下叶尖的动态响应特征。基于该动态响应特征仿真故障状态下的叶端定时信号，验证提出的故障算法有效性。为了简化模型复杂度，忽略轮盘与叶片接触面的刚度与阻尼效应影响，将单叶片模型简化为图 1所示的一端固定、一端自由的悬臂梁模型。叶片长度为L，宽度为b，厚度为w（b>w）。采用单自由度弹簧阻尼模型进行动力学建模。假设叶片材料为钢，质量为m；叶片刚度为k；叶片阻尼为c，叶片结构与材料参数如表 1所示。下文将基于以上假设分析不同故障类型下叶尖动态响应的变化规律。

表1 叶片结构与材料参数Table 1 Blade structure and material parameters

图1 单叶片简化模型Fig.1 Simplified single blade model

碰磨通常是由转子叶片与机匣间隙较小、叶片受热不均匀引起叶片拉伸变形，或转子不对中导致的。碰磨发生时间很短，通常只有毫秒级。本节基于碰磨发生初期的单点碰磨假设，将每次碰磨视为施加在叶尖的单位冲击，每旋转一圈碰磨一次，建立动力学模型，即

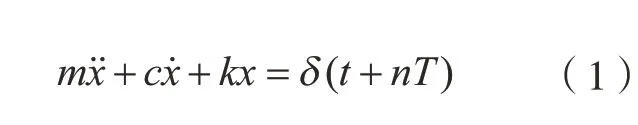
式中，T是叶片的旋转周期。本节对比了不同转速、不同阻尼比对碰磨状态下叶尖位移响应的影响。叶片振动的阻尼固有频率为1020 Hz，图2为阻尼比ζ= 0.01时不同转速叶尖位移响应，由图 2（a）可知，当旋转周期大于叶片振动周期，即振动频率大于转速时，碰磨带来的冲击效应会在一个旋转周期内衰减至0，相邻两个旋转周期内的碰磨响应没有重叠，碰磨响应的最大振幅为3 mm。图2（b）为旋转周期小于叶片振动周期，即振动频率小于转速导致的叶端定时通过频率，相邻几个旋转周期内的碰磨响应相互重叠，但仍可以从每一圈的叶尖位移数据中看出振荡衰减的趋势，叶尖位移的幅值在第2圈内达到峰值，之后逐圈减小并趋于平稳，趋于平稳时的叶尖振幅仍为3 mm。图2（c）为旋转周期继续减小至0.001 s，此时叶片振动频率近似旋转频率，相邻两转的碰磨响应高度重合在一起，不再表现为振荡衰减波型，叶尖的振幅先随时间增加，在约20圈处达到最大值，然后随时间减小并逐渐趋于稳定，稳定时的叶尖振幅约为20 mm，大于前两种情况。

图3为旋转周期T= 0.01 s时不同阻尼比下的叶尖位移响应。图 3（a）中，碰磨响应的振荡衰减时间小于旋转周期，因此各圈碰磨的响应之间没有重叠；由于阻尼比大于图 2（a），响应的最大幅值略小于3 mm。图3（c）为阻尼比ζ= 0.001时碰磨状态下的叶尖动态响应，此时叶尖位移表现为波动阶梯式衰减特性，以0.05 s为近似周期，每个周期出现4个不同幅值范围的阶梯振荡衰减波型，前3个阶梯的最大振幅随周期推进逐渐减小，第4个阶梯随周期推进逐渐增加，根据此规律4个阶梯的幅值逐渐趋于一致，最终表现为幅值约为2.5 mm的单频振动。

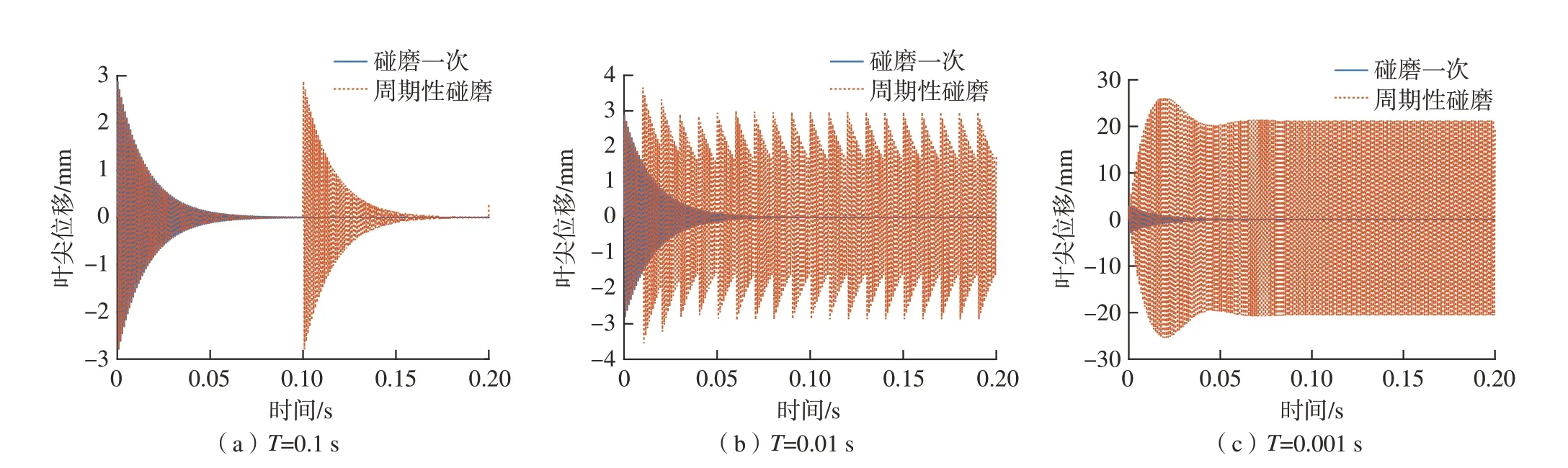
图2 ζ = 0.01时碰磨状态下不同转速叶尖位移响应Fig.2 Blade tip displacement under different rotating speeds when ζ = 0.01

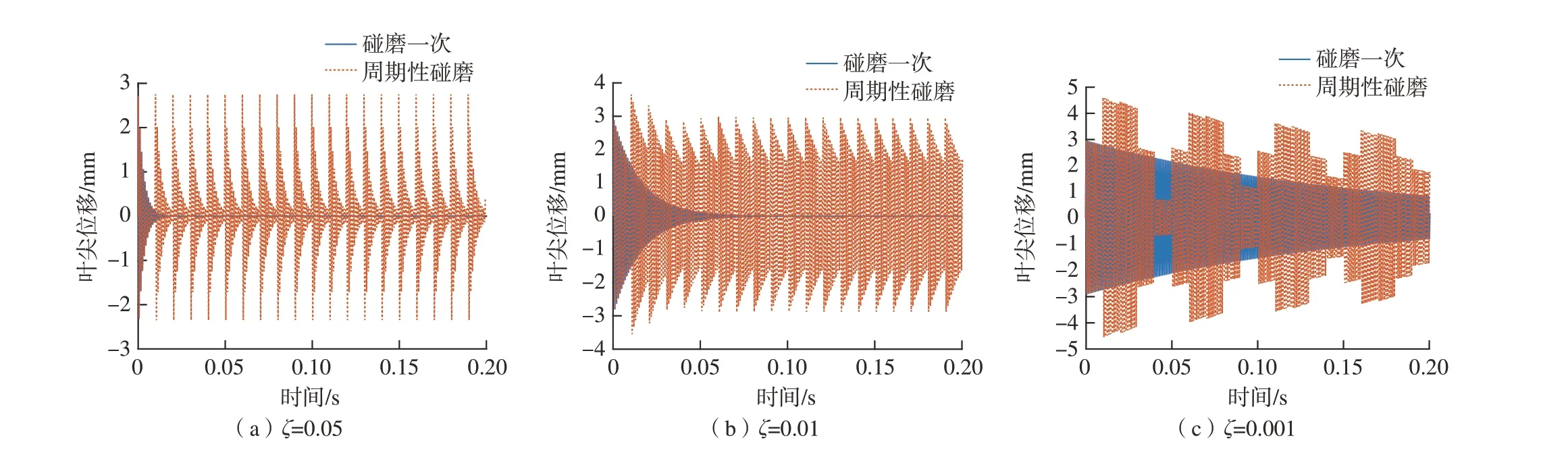
图3 T = 0.01 s时碰磨状态下不同阻尼比叶尖位移响应Fig.3 Blade tip displacement under different damping ratios when T = 0.01 s

2 碰磨状态下整级叶盘动力学建模

本节研究对象为图4所示的含8个叶片的整级叶盘在裂纹、外物打伤、碰磨等故障状态下的各叶片的叶尖动态位移响应。为了简化模型，将每个叶片建模为悬臂梁，将叶盘沿半径等分为8个扇区，每个扇区有叶片和轮盘两个自由度。假设叶片刚度为k1，叶片质量为m1，叶盘阻尼为c1，相邻叶片之间没有耦合；叶盘每个扇区刚度为k2，质量为m2，阻尼为c2，叶盘相邻扇区之间的耦合刚度为k3，耦合阻尼为c3；相邻扇区之间的耦合刚度为k4；耦合阻尼为c4。图5所示为图 4中整级叶盘模型简化后的集中参数模型。

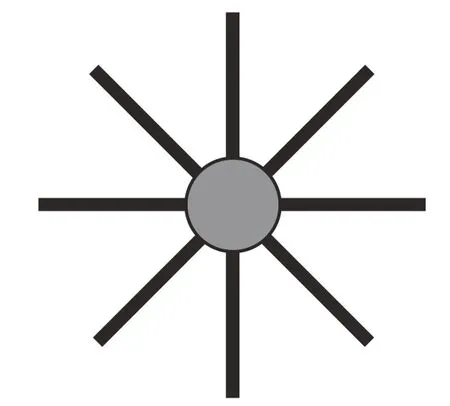
图4 整级叶盘简化模型 Fig.4 Simplified model of disk

根据图 5所示的整级叶盘集中参数模型，定义第i个叶片的位移为，叶盘第i个扇区的位移为，建立叶片与叶盘扇区在自由振动下的动力学方程组。

图5 整级叶盘集中参数模型Fig.5 Lumped parameter model of disk

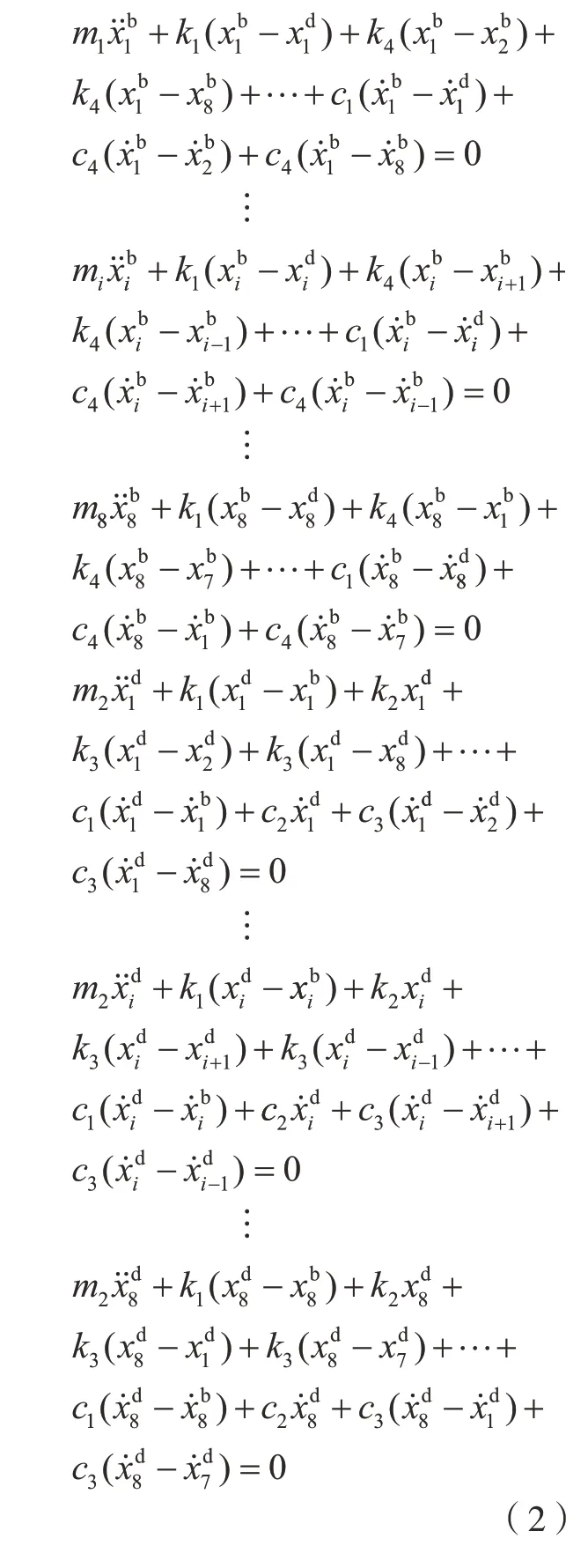
建立整级叶盘系统的动力学模型矩阵为

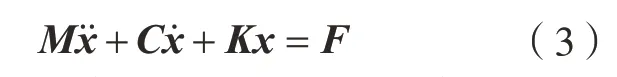
由式（2）可得叶盘系统的质量矩阵M、刚度矩阵K和阻尼矩阵C。

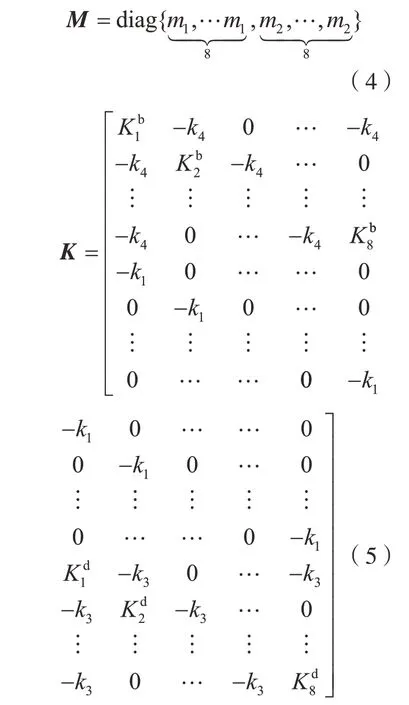
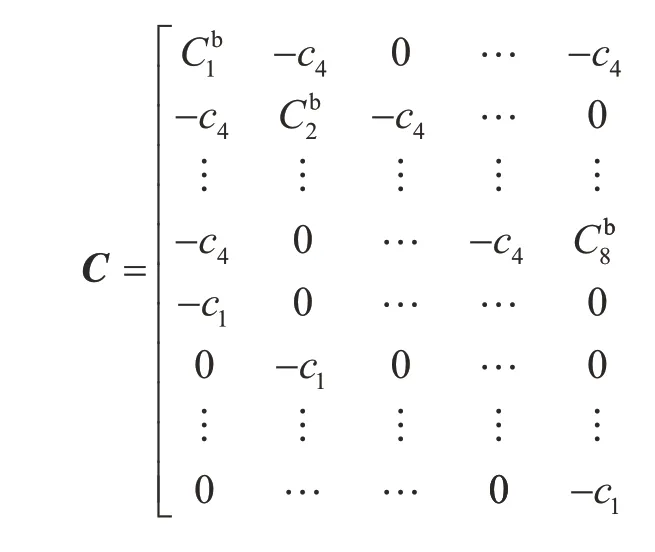
轮盘材料与叶片材料均为钢，无故障状态下叶片及叶盘其他参数设置如表 1和2所示。由于叶盘扇区刚度远大于单个叶片刚度，因此将叶盘假设为刚体，不再考虑k2、k3、c2、c3对叶片位移响应的影响。刚度矩阵K和阻尼矩阵C及位移矩阵x可写为

表2 叶盘结构与材料参数Table 2 Structure and material parameters of blisk

式中，耦合阻尼k4由耦合因子α和叶片刚度决定[20]。

对于单叶片碰磨和整级叶盘碰磨的动力学建模如式（10）和（11）所示。

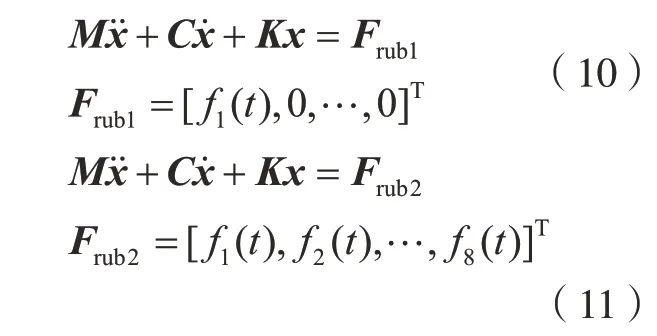
式中，fi（t）为周期性矩形脉冲信号。假设转子转速为100 Hz，叶盘旋转周期为0.01 s，每次碰磨冲击力的持续时间为旋转周期的1/100，碰磨力大小为100 N。由于碰磨通常发生于叶尖和机匣某一区域之间，因此当整级叶盘都存在碰磨时，碰磨之间的时间间隔为T/N（其中，T是旋转周期，N是叶片数目）。因此碰磨力Frub1和Frub2如图6所示。

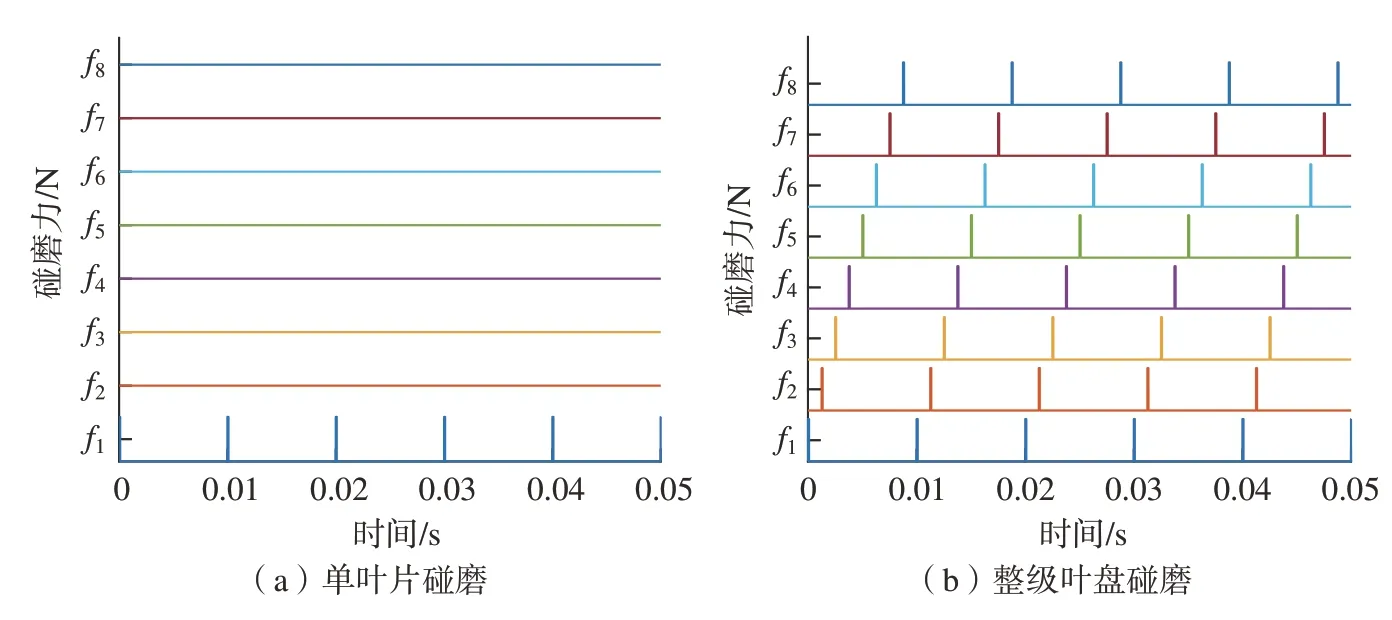
图6 碰磨状态下叶盘系统所受周期性冲击力Fig.6 Periodic force on blisk under rubbing conditions

求解式（10）和（11）得到叶盘系统所有叶片的叶尖位移响应，如图 7所示，当仅有1号叶片存在碰磨时，1号叶片的叶尖信号在每转中呈振荡衰减特性，由于叶间的耦合作用，其他叶片的叶尖也存在振动现象，其中最靠近1号叶片的2号和8号叶片的振动最明显，3号和7号叶片也存在较为明显的振动，其他叶片由于距离1号叶片较远，因此耦合作用微弱可忽略。

图7 碰磨状态下叶盘系统的叶尖位移响应Fig.7 Blade tip displacement of blisk under rubbing conditions

图8 （a）对比了振动最明显的1～3号叶片的叶尖位移振动特性，其中2号叶片在第1圈位移逐渐增加，第2圈保持在0.05左右，从第3圈开始则表现为幅值较小的波动信号；3号叶片首先表现为振幅逐渐增加的振荡信号，并于第3圈达到振幅最大值，随后逐渐减小。当整级叶盘的叶尖都存在碰磨现象时，各叶片都表现为周期性的振荡衰减信号，对比1～3号叶片的叶尖位移数据（图8（b））可以看出，1～3号叶片均在碰磨发生的第1圈振幅最大，随后逐圈衰减并趋于平稳。

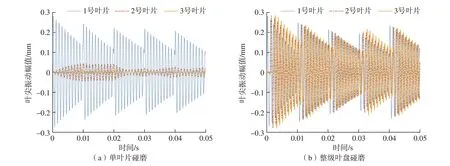
图8 碰磨状态下1～3号叶片的叶尖位移响应Fig.8 Blade tip displacement of blade 1-3 under rubbing conditions

图9为两种碰磨状态下叶盘系统的叶尖振幅特性，可以看出，当仅有一个叶片存在碰磨现象时，该叶片的振幅最大，其他叶片距离碰磨叶片越远，振幅越小，5号叶片受碰磨影响最小。当所有叶片都发生碰磨时，微弱的差距体现在振动周期开始的时间以及振幅上，最早发生碰磨的叶片，例如1号叶片的振幅中位数（0.0220 mm）最大，但上限（0.2816 mm）最小；而距离1号叶片最远的5号叶片振幅中位数（0.0041 mm）最小，但振幅上限（0.2993 mm）最大，但各叶片振幅差距不明显，不同叶片振幅上限的差距仅为5%。

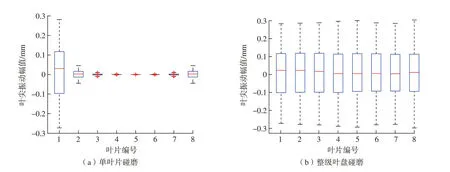
图9 碰磨状态下叶盘系统的叶尖振幅特性Fig.9 Blade tip amplitude feature of blisk under rubbing conditions

3 碰磨诊断指标

根据推导可知叶片碰磨故障可以建模为每圈一次的单位冲击，此时的激励频率即为转子的转速。假设转速为9000 r/min，分别分析叶片固有频率为600 Hz和550 Hz时的叶尖频谱。上述两种固有频率的假设代表了碰磨激励起同步共振和异步共振的两种状态，叶片阻尼比为0.03。传感器布局设置为[72°，144°，216°，288°，359°]，叶端定时系统采样数据如图 10所示（其中蓝色实线为高采样率叶尖振动位移，红点为叶端定时采样结果，框内为同一传感器在10圈内采集的数据）。

异步共振时激励频率不是转速的整数倍，各传感器在不同圈采集到的振动相位不同。但由图10可知，针对碰磨引起的叶尖响应，即使激励频率与固有频率没有整数倍关系，同一传感器在各圈采集到的振动相位都相同；此外由于各圈数据大同小异，因此从叶端定时信号中难以观测出振荡衰减的特征；但当叶盘一致性较好，即所有叶片的固有频率相同时，由于碰磨位置与传感器安装位置的相对角度不变，此时传感器采集到的不同叶片的振动相位也相同。

针对图 10（a）中的实线信号，即满足香农采样定理的叶尖位移信号进行频谱分析，对比不同阻尼比对频谱的影响。由图11可知，碰磨状态下的叶尖位移信号频谱以固有频率为主频，以转频为边频带。对比图11（a）～（c）可知，叶片的阻尼比越大，边频带越高。

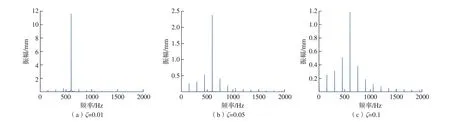
图11 叶尖信号频谱分析Fig.11 Frequency spectrum of blade tip signal

分别采用最小二乘谱图（LSP）、迭代重加权谱图（IARLSP）[21]和增强稀疏分解（ESD）[22]对图10（a）中的叶端定时信号进行分析得到如图12所示的结果。由图12（a）可知，LSP含有的频谱信息最丰富，但这可能是频谱混叠导致的；图12（b）中转频成分最大，这是由于碰磨状态下的叶端定时信号为高度欠采样信号，且由于各圈采集的相位相同，因此从叶端定时信号特征出发，转频占比最大；而图12（c）中增强稀疏分解得到的谱图受混叠干扰最小，但也遗失了一定的转频边频带信息。

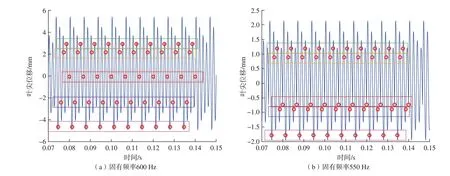
图10 碰磨仿真时域数据Fig.10 Simulation data of rubbing blade

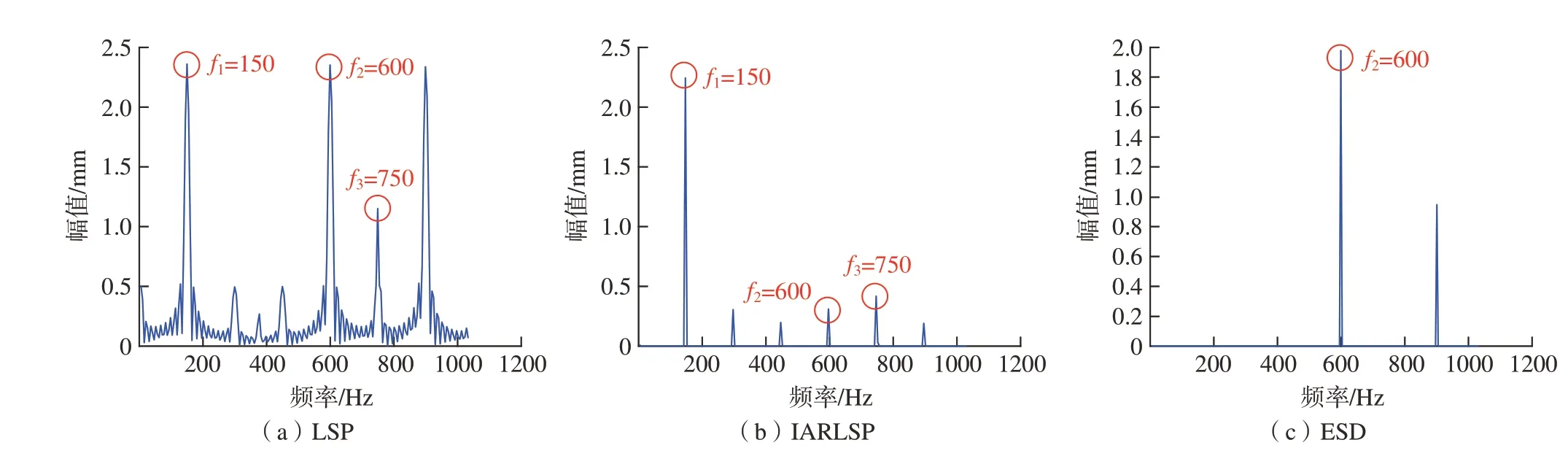
图12 碰磨状态下叶端定时信号谱图分析Fig.12 Frequency spectrum of blade tip timing signal under rubbing conditions

综上所述，可以提出如下碰磨判别指标：

（1）观察信号频谱是否含有固有频率和转频边频带；

（2）同一叶片同一传感器不同圈采集相位是否相同（用于确定某一叶片是否存在碰磨）；

（3）所有叶片同一传感器在同一圈内采集相位是否相同（确定所有叶片都存在碰磨，仅适用于所有叶片固有频率相同的情况）。

根据上述指标提出图13所示碰磨故障诊断流程。当叶片发生同步共振时，同一传感器在邻近几圈采集到的相位信息相同，因此其时域信号的互相关值表现为趋近于1的现象[21]。由图10可知，碰磨时的时域信号与同步共振类似，因此分别针对每个叶片进行相邻圈数据的互相关值分析以判断是否存在相位相同的情况，对互相关值持续较高区域进行频谱分析，若存在以固有频率为主频，以转频为边频带的现象，则判断此叶片出现了碰磨，若仅有一个叶片出现碰磨则故障原因可能是此叶片伸长，若所有叶片均出现碰磨则故障原因可能是机匣变形或转子不对中。

图13 碰磨故障诊断流程Fig.13 Rubbing fault diagnosis procedure

4 试验验证

本节采用课题组自主搭建的如图14所示的试验台进行碰磨诊断方法验证。该试验台含有碰磨模块（图14（a）中红框），该模块由电机驱动，可沿x、y、z3个方向微动，用于模拟机匣变形引起的整级叶盘于固定点碰磨故障。叶盘为钢制六直叶片整体叶盘，采用5个传感器进行叶端定时采样，传感器安装角度为[0，59.84°，79.55°，104.93°，145.38°]。

图14 碰磨试验台Fig.14 Rubbing test rig

对匀速状态下碰磨的叶尖位移数据进行测量得到各叶片数据如图15（a）所示，在红框内出现了振幅持续增大的现象，猜测可能是由碰磨引起的。因此采用图 13提出的诊断流程进行诊断。首先得到各叶片的互相关值如图15（b）所示，可知各叶片在红框内均出现了互相关值趋于常数的现象，其中3～6号叶片明显增加到1附近，1号和2号虽然没有增加至1，但也略有增加，相对于时域图可以更明显地看出变化。

如图16（a）所示，是振幅增加最多的4号叶片的各传感器数据，可知在振幅增加区域，同一叶片的同一传感器在不同圈采集相位相同，符合上文提出的碰磨故障判别指标的第2条。对第1个碰磨区域的信号进行增强稀疏分解得到频谱图（图16（b）），其中出现了明显的以固有频率548 Hz为主频，以转速3600 r/min为边频带的频谱特征，由此诊断4号叶片出现了碰磨现象。

图16 4号叶片时域及频域数据Fig.16 Time and frequency domain data of blade 4

对所有6个叶片的数据进行视频分析得到时频图如图17所示。可知各叶片均发生了碰磨现象，但碰磨导致的叶尖响应幅值不同，其中1号叶片碰磨程度最小，这可能是由于叶片长度不均匀导致的。

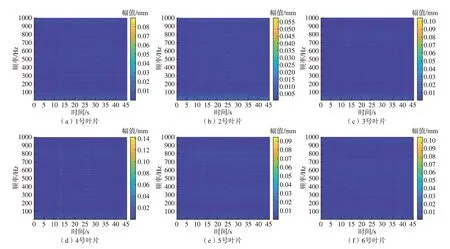
图17 碰磨状态下所有叶片时频图Fig.17 Time-frequency diagram of all blades under rubbing conditions

5 结论

碰磨是航空发动机转子叶片常见故障，本研究以叶片健康监测与故障诊断为目标，对转子叶片和叶盘进行了动力学建模，得到了叶尖动态响应规律，并据此提出了一套基于叶端定时系统的碰磨诊断流程。

针对单叶片建立了单自由度悬臂梁简化模型，揭示了碰磨故障模式下的叶尖振动位移响应。对比了转速和阻尼比对碰磨状态下叶尖动态响应的影响规律，每个转动周期内叶尖位移信号为振荡衰减信号，转速和阻尼比决定转动周期间的重叠率。针对整级叶盘建立了多自由度叶片耦合模型，分析了单叶片碰磨和所有叶片碰磨状态下的叶尖位移响应规律，当仅有一个叶片存在碰磨现象时，该叶片的振幅最大，其他叶片距离碰磨叶片越远，振幅越小；当所有叶片都发生碰磨时，各叶片均表现为周期性振荡衰减信号，区别仅在于周期开始的时间。