钢渣细骨料混凝土单轴受压应力-应变关系试验研究
薛 刚,付 乾,周海峰,孙立所
(内蒙古科技大学土木工程学院,内蒙古 包头 014010)
我国是钢铁大国,钢产量居世界第一,2020年,我国粗钢产量为 10.53亿吨,同比增长5.2%[1],占世界粗钢总产量的比例超过50%[2].钢铁工业快速发展的同时,钢铁炉渣的产生量大幅增加.每炼1吨钢大约产生125 ~ 140 kg钢渣[3],我国钢渣年产生量已超过约1亿吨,年堆存量不断攀升.我国钢渣的主要利用途径有:钢渣粉、钢渣水泥、硅酸盐水泥配料、钢渣砖及道路材料[4],钢渣的综合利用率为50% ~60%,与日本、美国等发达国家的钢渣利用率相比还有较大差距.长期堆存的钢渣风化后产生大量粉尘,污染空气,集中堆放过程中,大量成分进入土壤会使土质改变、破坏土壤结构,污染土壤,不利于可持续发展.研究钢渣的资源化利用既利于环保,同时能够带来显著的经济效益.
目前,我国社会建设步伐突飞猛进,混凝土需求量不断增加,混凝土中的天然骨料总量是有限的,石子、砂等天然资源的匮乏问题已日益凸显.我国的钢渣大多为转炉钢渣,其矿物组分主要包括硅酸二钙、硅酸三钙、铁铝酸钙、RO相以及少量的游离氧化钙等.钢渣的化学组成与硅酸盐水泥相似且具有一定的胶凝活性,可代替部分水泥作为掺合料应用于混凝土中,但钢渣粉磨工艺能耗较高,市场接受程度偏低,没有得到广泛应用和推广.钢渣相对于传统天然骨料具有高密度、抗压强度、易磨指数低等优点,近年来,将钢渣进行粒化作为粗骨料或细骨料制备钢渣混凝土(steel slag concrete,SSC)得到工程界和学术界的广泛关注[5-6].朱训国等[7]研究表明,在相同水胶比下配制C30强度等级的钢渣细骨料混凝土,各龄期强度随钢渣掺量的增加先增加后减小;在制备C30以下低强度混凝土时,完全可以考虑采用钢渣大掺量代替细骨料.韩艳丽等[8]研究表明,钢渣粗骨料或钢渣细骨料掺入混凝土后均可提高基本力学性能,钢渣细骨料的最优掺量为50%,且钢渣细骨料对混凝土强度提高效果比钢渣粗骨料大.Qasrawi等[9]研究了钢渣用作细骨料对混凝土的影响,当钢渣代替量为30% ~ 50%时,各龄期的抗拉强度可达到基准样的1.4倍 ~ 2.4倍,其中50%掺量时抗拉强度提高效果最好.当钢渣掺量为15% ~ 30%时,各龄期抗压强度提高效果最好.目前对钢渣混凝土基本强度方面的研究较多,有关钢渣细骨料混凝土应力-应变关系方面的研究报道还不够充分,于峰等[10]建立了补偿收缩钢渣粗骨料混凝土应力-应变关系模型,该模型计算结果与试验结果吻合较好.李斌等[11]研究表明,水淬钢渣细骨料掺量为60%时钢渣混凝土强度最高、性能最好,对无量纲化应力-应变全曲线进行拟合,拟合结果与实测结果吻合良好.
本文采用包钢集团的钢渣部分替代细骨料制备钢渣混凝土.对钢渣进行物理化学性能试验,研究钢渣细骨料在混凝土中的适用性;对钢渣混凝土进行单轴受压试验,研究钢渣细骨料掺量对混凝土抗压强度及本构关系的影响规律,建立其单轴受压应力-应变关系,为钢渣用于混凝土工程提供试验及理论依据.
1 试验概况
1.1 试验原材料
根据国家标准《通用硅酸盐水泥》(GB 175—2007)[12]使用普通硅酸盐水泥P•O42.5和包头本地的天然砂及石子,其物理性能符合《建设用砂》(GB 14684—2011)[13]及《建设用卵石、碎石》(GB/T 14685—2011)[14]规范要求.采用包钢集团公司的钢渣细骨料,其粒径大多在5 mm以内,级配符合《建设用砂》(GB 14684—2011)[13]要求,其级配曲线如图1所示.钢渣细骨料表面粗糙多孔洞,其物理形貌如图2所示.利用X射线荧光光谱仪对钢渣进行光谱半定量全分析得出钢渣的主要化学成分如表1所示,其游离氧化钙含量为1.2%,符合规范要求.研究表明[15],包钢钢渣的放射性比活度小于建筑材料用工业废渣放射性物质限值标准,将钢渣再加工后用于建筑材料,不会出现放射性污染问题.本文试验用砂、钢渣、石子的物理性能指标见表2.

表1 钢渣主要化学成分Tab.1 Main chemical composition of steel slag
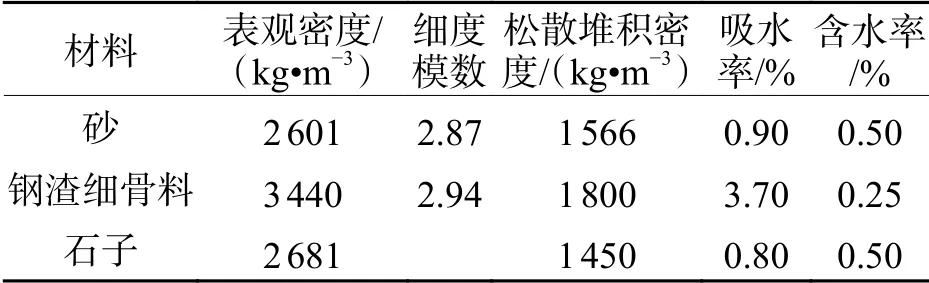
表2 骨料物理性能指标Tab.2 Physical properties of aggregate
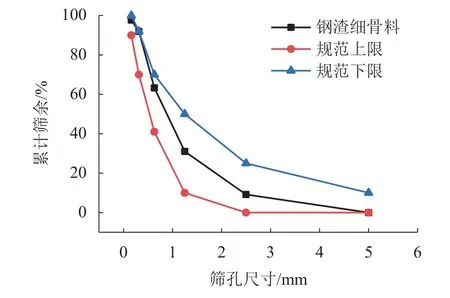
图1 钢渣细骨料级配曲线Fig.1 Grading curves of steel slag fine aggregate

图2 钢渣细骨料Fig.2 Steel slag fine aggregate
1.2 钢渣稳定性
本文依据《钢渣稳定性试验方法》(GB/T 24175—2009)[16]对钢渣骨料进行压蒸粉化率试验,测定钢渣的稳定性.
压蒸粉化率试验原理为:在2.0 MPa的饱和蒸汽条件下压蒸钢渣,使其中所含游离氧化钙、游离氧化镁消解粉化,通过粉化率判断钢渣的稳定性.具体方法为:1)将称量好的自然粒级为4.75 ~ 2.36 mm的钢渣放在压蒸釜中,压蒸釜置于压蒸屉内,将盛放压蒸屉的电热鼓风箱温度调整到216 ℃,在2.0 MPa的饱和蒸汽压力下蒸3 h,冷却后取出所有钢渣并烘干,质量为m0;2)在振筛机上用1.18 mm筛振20 min后,称量筛余钢渣质量m1.渣样粉化率f按式(1)计算.

选取两份钢渣试样测定压蒸粉化率,结果分别为1.760%和1.770%,均值为1.765%.截至目前,还没有国家规范对钢渣压蒸粉化率的限定,黑色冶金行业标准《普通预拌砂浆用钢渣砂》(YB/T 4201—2009)[17]及《水泥混凝土路面用钢渣砂应用技术规程》(YB/T 4329—2012)[18]中规定,钢渣压蒸粉化率应≤5.900%,本文所用钢渣满足这两个行业规范要求.
1.3 配合比设计
钢渣混凝土配合比依据《普通混凝土配合比设计规程》(JGJ 55—2011)[19]进行设计,基准水胶比为0.45,钢渣细骨料分别以10%、30%、50%、70%、100%的替代率等质量替代天然砂制备钢渣混凝土.研究表明[20-21],钢渣的掺入对混凝土工作性能产生不利影响,故掺入57 kg/m3粉煤灰并调整减水剂用量来改善钢渣混凝土的工作性能,使钢渣骨料混凝土与普通混凝土具有相近的坍落度.钢渣混凝土配合比如表3所示,表中:NC为普通混凝土;SSC为钢渣混凝土,SSC后的数字为钢渣细骨料替代百分率.
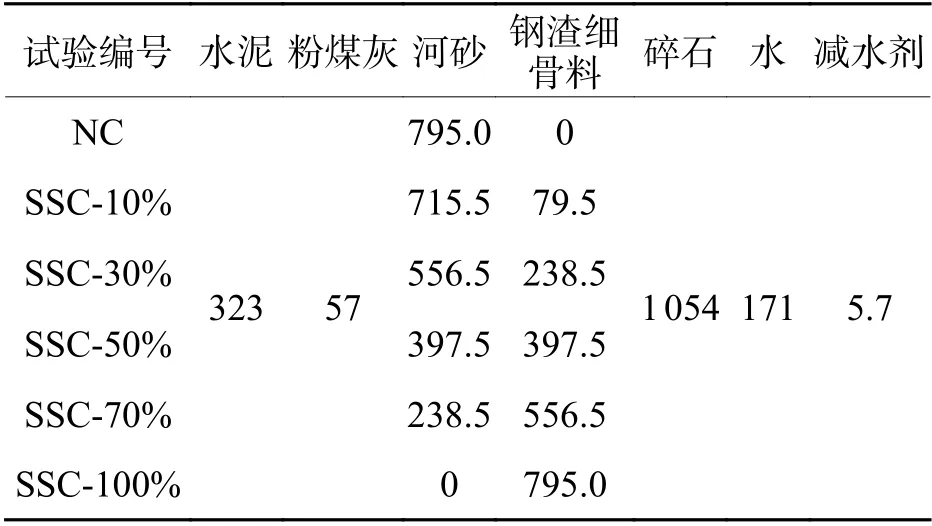
表3 钢渣细骨料混凝土配合比Tab.3 Mix proportion of steel slag fine aggregate concretekg
1.4 试验方法
按照表3中的配合比制备6组立方体试件及棱柱体试件.试验依据《混凝土物理力学性能试验方法标准》(GB/T 50081—2019)[22].
棱柱体受压试验在微机控制电液伺服压力机上进行,用两个1000 kN的液压千斤顶作为附加刚性元件,增加试验装置的整体刚度,以防混凝土突然破坏,该试验装置能够测得混凝土受压应力-应变曲线下降段.在试件两侧放置两个位移计以测量竖向位移,另外两侧分别在竖向和横向的中心线处粘贴混凝土应变片用于以测量应力-应变曲线上升段混凝土的应变.在应力达到约75%极限应力之前,试验加载速度为0.010 mm/s;在应力达到75%极限应力之后,试验加载速度调整为0.003 mm/s.试验中采用DTS-530型高速静态数据采集仪自动采集,棱柱体试件受压应力-应变曲线试验测试装置如图3所示.

图3 钢渣混凝土棱柱体轴心抗压试验装置Fig.3 Axial compressive test apparatus for steel slag concrete prisms
2 试验结果与分析
2.1 破坏形态
2.1.1 立方体试件
钢渣骨料混凝土立方体试件与普通混凝土立方体试件破坏形态相似.在加载初期,混凝土没有明显的裂缝.随着应力的增大,试块产生压缩变形,在试块左右两侧边缘出现竖向裂缝;试块向外鼓曲,伴随着轻微的噼啪声,试件表面的混凝土颗粒掉落,最终破坏形态为两个对顶的角锥.由于环箍作用,在试件上、下表面附近破坏程度较轻,试件中部受摩擦约束效应较小,所以破坏程度最大.钢渣骨料含量较高时,混凝土破坏突然且发出较响的崩裂声,呈明显的脆性,立方体试件破坏形态如图4所示.

图4 混凝土立方体试件破坏现象Fig.4 Failure phenomenon of concrete cube specimens
2.1.2 棱柱体试件
不同替代率的钢渣骨料混凝土的破坏过程相近,但脆性特征不同,破坏形态见图5.主要有以下3个阶段:

图5 普通混凝土及钢渣细骨料混凝土轴压破坏形态Fig.5 Failure modes of ordinary concrete and steel slag fine aggregate concrete under axial compression
1)弹性阶段:荷载较小时钢渣混凝土产生弹性变形,混凝土内部微裂缝的扩展与已有微裂缝的压缩平衡,处于相对稳定期,因此试件宏观变形较小.
2)弹塑性阶段:随着荷载的增加,在混凝土试件长轴方向的边缘出现微小的竖向裂缝,随着荷载增加,该竖向裂缝逐渐延伸,同时有轻微的劈裂声,试件表面有零星的混凝土掉落.荷载继续增大,混凝土内部微裂纹联通并扩展,试件表面裂缝也随之发展.为防止试件爆裂,此后加载由荷载控制改为位移控制.此阶段内部原有裂缝逐渐贯通,新裂缝大量产生,试件表面裂纹宽度逐渐增大,混凝土内部水泥砂浆与骨料逐渐失去黏结作用,竖向压缩应变增长较快,试件侧向膨胀,试件的竖向裂缝逐渐增多,随后混凝土达到峰值应力.
3)破坏阶段:应力超过峰值应力后,混凝土骨料与水泥浆体之间的胶结力、摩擦力等粘结作用被破坏,试件逐渐破裂,并沿对角方向出现一条主裂缝,混凝土的剥落现象明显.
2.2 棱柱体抗压强度与立方体抗压强度的换算关系
普通混凝土棱柱体抗压强度fc与立方体抗压强度fcu的比值为0.76 ~ 0.82[23],本文测得的6组钢渣细骨料混凝土立方体抗压强度及棱柱体抗压强度的数据(表4)表明:钢渣细骨料混凝土棱柱体抗压强度与立方体抗压强度的比值为0.80 ~ 0.86,略高于普通混凝土棱柱体抗压强度与立方体抗压强度的比值.主要原因在于,掺入钢渣细骨料后,混凝土强度更高、弹性模量更大,且随着钢渣骨料替代率的增加,立方体抗压强度随之增大,试验机加载板对钢渣骨料混凝土的环箍作用对强度的影响相对减弱,致使混凝土单轴抗压强度与立方体抗压强度的比值提高.利用最小二乘法可建立钢渣混凝土棱柱体抗压强度fc(ssc)和立方体抗压强度fcu(ssc)比值与替代率r的换算关系,如式(2).
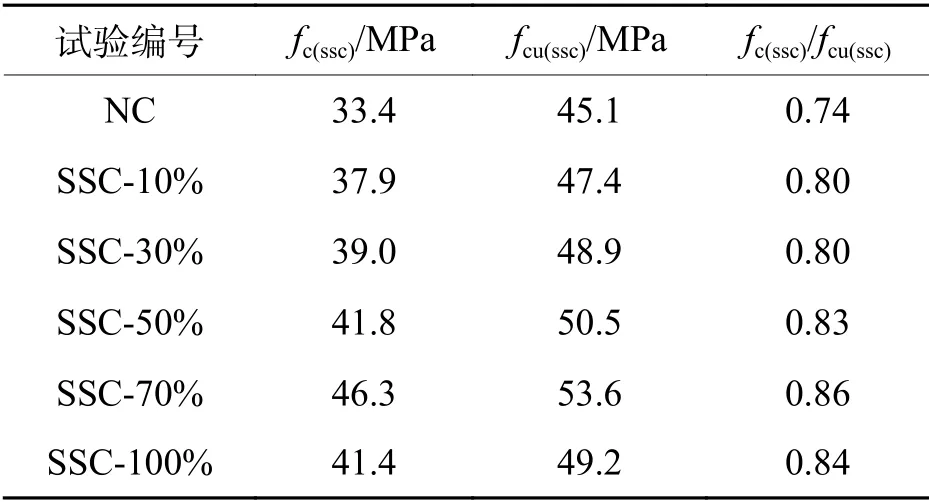
表4 棱柱体抗压强度与立方体抗压强度Tab.4 Prism compressive strength and cube compressive strength
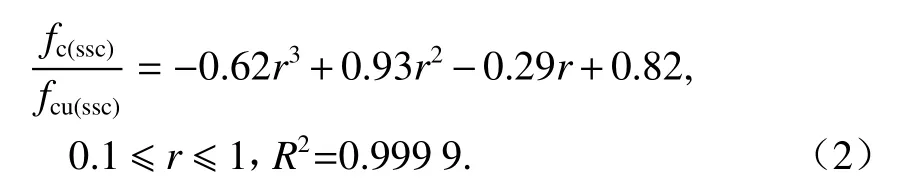
式(2)与文献[7]得到的函数关系差别明显,利用本文的钢渣混凝土立方体强度试验值,按照文献[8]推定的轴心抗压强度与本文试验结果相差12% ~ 18%,主要原因在于钢渣混凝土轴心抗压强度与立方体抗压强度的函数关系与钢渣骨料类型、粒径、掺量密切相关.
钢渣骨料掺量过高时 (高于70%),钢渣对混凝土强度的增强幅度减缓,主要原因在于钢渣吸收的水分较多,影响胶凝材料的充 分水化,甚至存在未完全水化的胶凝颗粒;钢渣吸收的水分多,造成混凝土流动性降低,对密实度产生不利影响,孔隙及微小裂缝随之增多,钢渣细骨料增强混凝土立方体试件抗压能力降低.
2.3 应力-应变全曲线
图6为应力-应变关系曲线测试结果.由图6可以看出:
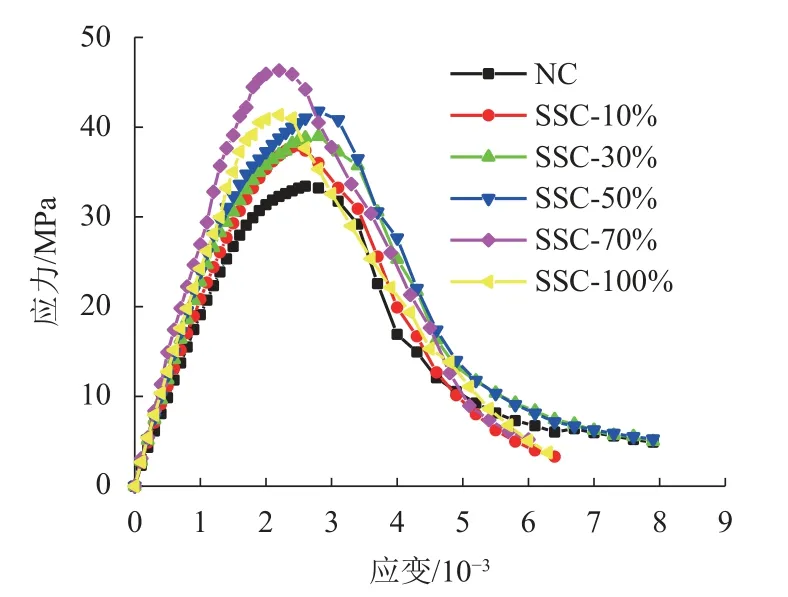
图6 钢渣细骨料不同替代率下混凝土单轴受压应力-应变曲线Fig.6 Stress-strain curves of concrete under uniaxial compression under different substitution rates of steel slag fine aggregate
1)钢渣细骨料混凝土与普通混凝土应力-应变曲线均先上升后下降.在加载初期(0.5fc(ssc)),应力-应变曲线接近直线,但是不同钢渣细骨料掺量的混凝土上升段的斜率有所不同,掺钢渣细骨料的混凝土上升段斜率明显高于普通混凝土,说明钢渣骨料的掺入提高了混凝土的刚度;0.5fc(ssc)∼fc(ssc)应力-应变曲线斜率变小,应变增长速度逐渐大于应力增长速度,掺钢渣细骨料混凝土的峰值应力与普通混凝土相比明显增大,说明钢渣骨料的掺入可以使混凝土单轴抗压强度增大.
2)峰值应力后,应力-应变曲线进入下降段,钢渣骨料混凝土的下降段较普通混凝土下降段稍缓,说明钢渣细骨料的掺入一定程度上增大了混凝土破坏时的极限应变.
3)根据表4可知,与钢渣细骨料替代率为70%的钢渣混凝土相比,钢渣细骨料替代率为100%的钢渣混凝土抗压强度仅降低 8.2%,从强度及经济性两方面看,钢渣细骨料替代率可取100%.
3 钢渣混凝土受压本构关系
3.1 模型确定
对于混凝土受压应力-应变关系模型,不少学者提出了多种表达式.经过对多种计算模型的对比研究,本文采用Carreira and Chu模型[24]、Wee模型[25]、过镇海提出的两段式应力-应变模型[26]对钢渣细骨料混凝土应力-应变关系曲线进行拟合分析.
Carreira and Chu提出的表达式具有数学表达式简单、上升段与下降段采用同一个方程以及参数计算较为简便的特点,其表达式为

式中:y=σ/fc,σ为应力;x=ε/εc,ε为应变,εc为混凝土峰值应变;β为模型参数,Ec为混凝土弹性模量,Ec=10200(fc)1/3.
1996年Wee对强度范围为50 ~ 120 MPa的混凝土单轴受压应力-应变全曲线进行了试验究,并建立了混凝土的本构模型,该模型在Carreira and Chu模型基础上进行了改进,采用同一表达式描述混凝土应力-应变关系曲线的上升段及下降段,且具有形式简单、适用性强的特点,表达式为
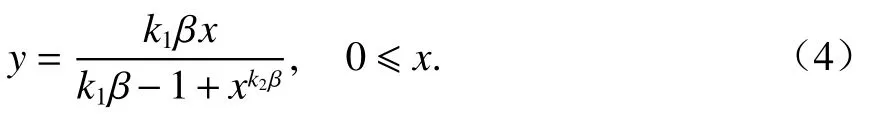
式中:k1、k2为下降级的脆性特征.
当混凝土强度fc≤50 MPa时,k1及k2均取1,此时的模型表达式与式(3)等效;当混凝土强度为50 MPa≤fc≤120 MPa时,k1=(50/fc)3,k2=(50/fc)1.3,k1及k2均小于1.
过镇海提出的混凝土单轴受压应力-应变关系表达式为分段形式,以峰值应力点为界限,分为上升段和下降段,上升段为多项式函数,下降段为有理分式函数,其表达式为
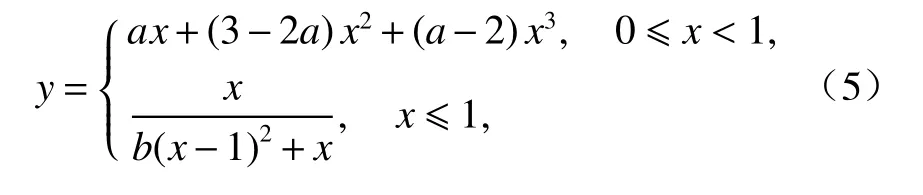
式中:a,b均为过镇海模型的参数,a为上升段参数,b为下降段参数.
文献[17]对该式中的参数做了详细的分析.a值越大,表明混凝土原点切线模量和峰值割线模量比值越大,材料延性越好.下降段参数b表达了下降段曲线的陡峭程度,b值越大,下降段曲线越陡峭,材料脆性越大.
对试验数据进行无量纲化处理,并分别利用Carreira 和 Chu 模型、 Wee 模型、 过镇海3种模型及本文建议模型对试验数据进行非线性拟合,结果见图7.拟合结果表明:Carreira and Chu模型全曲线上升段会明显低估钢渣混凝土的应力而下降段会高估应力;过镇海模型可较好拟合钢渣细骨料混凝土应力应变关系的上升段,但参数a不满足该模型的允许范围,同时下降段拟合效果较差;Wee模型上升段出现了应力大于1的情况,不符合应力-应变关系曲线特征,但下降段可以很好地拟合试验结果.
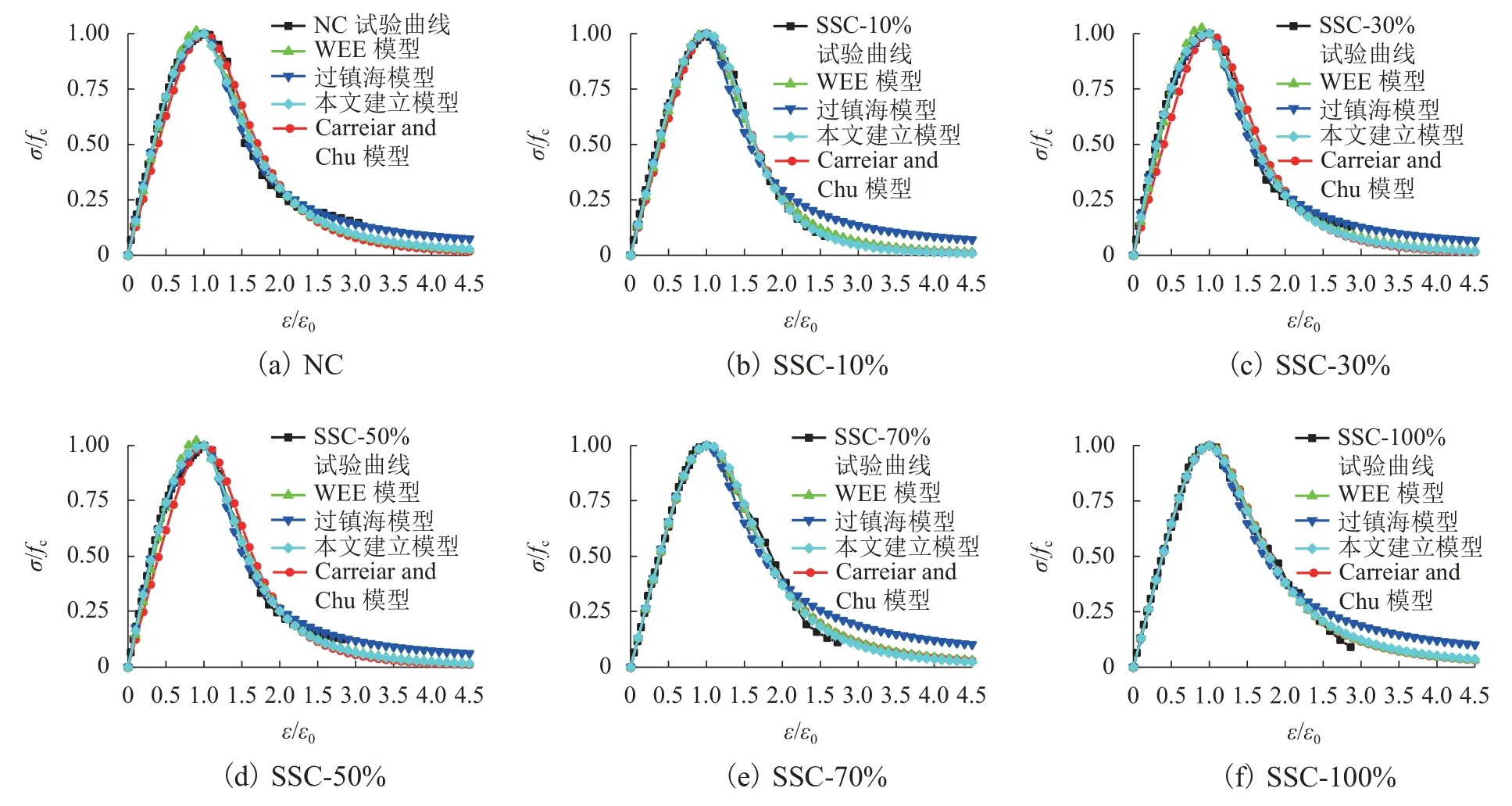
图7 试验曲线与模型曲线对比Fig.7 Comparison of test curves and modelt curves
根据钢渣细骨料混凝土的应力-应变关系试验结果,及3个模型的拟合效果,本文建议采用分段式模型对钢渣细骨料混凝土受压本构关系进行描述,上升段采用Carreira and Chu模型,下降段采用Wee模型,表达式为
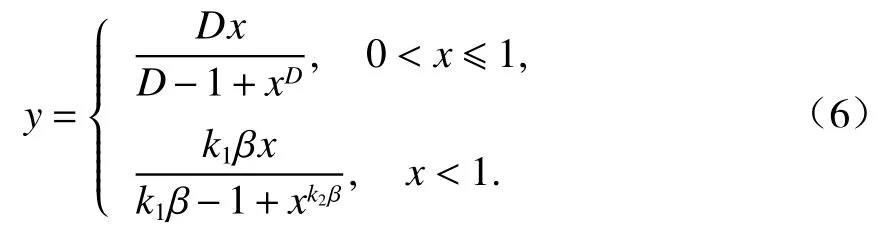
式中:D为上升段参数.
由图7模型曲线与试验曲线对比可知,本文建议的本构模型无论上升段还是下降段均与试验曲线吻合较好.图8为确定系数对比结果,对不同本构模型的确定系数及取值区间进行对比可知,本文模型的确定系数均值最接近1,确定系数的取值区间更小,且取值下限与取值上限均高于其他模型,表明本文提出的模型可以更好地描述钢渣细骨料混凝土应力-应变关系.
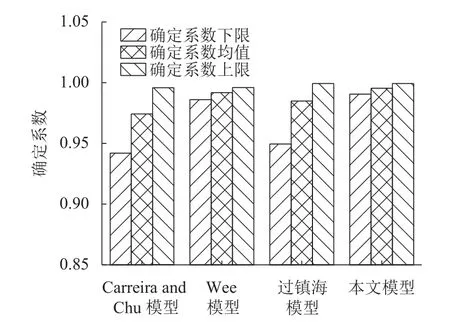
图8 确定系数及取值区间Fig.8 Determine coefficient and value interval
3.2 模型参数计算分析
3.2.1 推定模型的上升段模型参数D
为得到钢渣混凝土应力-应变关系曲线参数,将本文模型拟合所得的参数D与钢渣骨料的替代率r及fc(ssc)建立函数关系,上升段参数表达式为
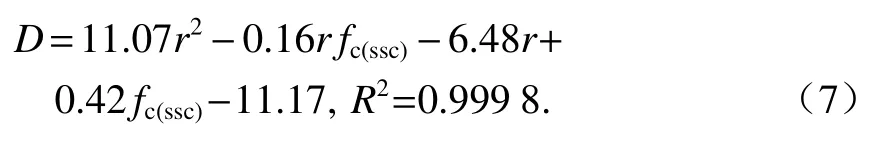
钢渣混凝土本构关系上升段参数D的物理意义与Carreira and Chu模型参数 β相同,表示割线弹性模量与原点弹性模量的关系,该值越大,表示上升段越陡峭,如式(8).
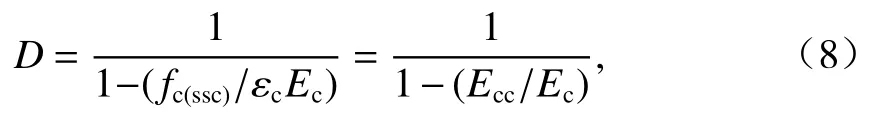
式中:Ecc为峰值割线模量(N/mm2).
为进一步分析参数D与钢渣替代率的关系,将式(7)简化为自变量仅含替代率r的函数.根据本文试验结果,钢渣混凝土棱柱体抗压强度fc(ssc)和普通混凝土棱柱体抗压强度fc的比值与替代率的关系为
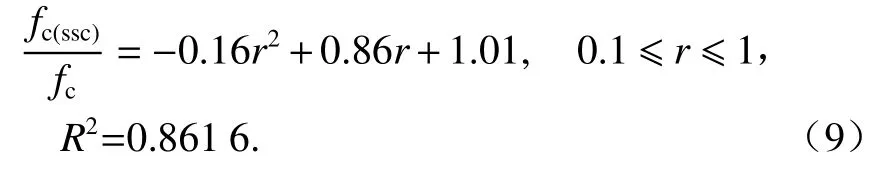
因此,钢渣混凝土棱柱体抗压强度与替代率的关系可表示为
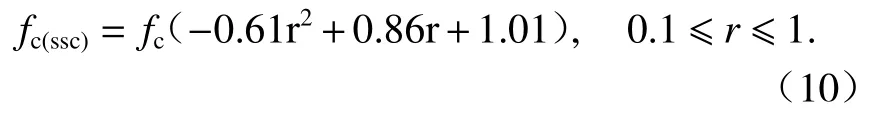
将式(10)代入式(7)可得到用钢渣替代率表达的上升段参数的计算公式.
图9为上升段参数D对应力-应变关系曲线的影响,图10为上升段参数公式中D值随钢渣骨料替代率的变化情况.由图10可知,参数D随钢渣细骨料替代率的增加,起初变化不大后明显增大.由式(8)可知:Ecc/Ec比值与参数D呈正相关关系,较低替代率时,钢渣细骨料对Ecc/Ec比值影响较小;高替代率时,钢渣细骨料可明显提高混凝土变形模量,且对峰值割线模量的提高幅度大于对原点弹性模量的提高幅度.
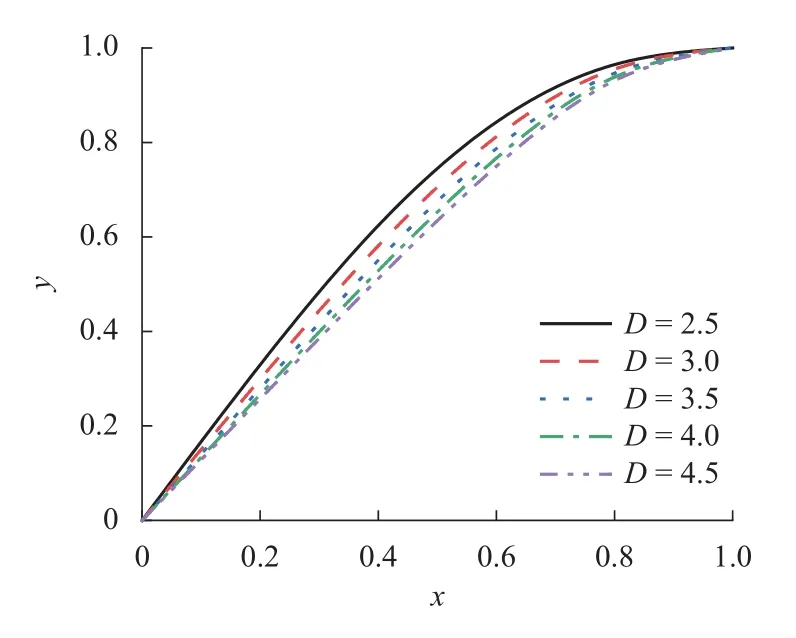
图9 上升段参数D对曲线的影响Fig.9 Influences of ascending stage parameter D on the curves

图10 上升段参数D与替代率关系Fig.10 Relationship between the ascending stage parameter D and the substitution rate
3.2.2 下降段参数k1、k2、β
Wee模型规定,当混凝土强度≤50 MPa时,下降段的脆性特征参数k1、k2均为1,此时模型与Carreira and Chu模型等效.本文钢渣混凝土强度均小于50 MPa,理应采用Carreira and Chu模型进行拟合,但对比拟合所得参数可知,采用Carreir and Chu模型进行拟合得到的下降段参数取值过于保守,本文推断与钢渣混凝土的脆性特性有关.本文的试验变量为钢渣替代率,利用MATLAB软件并选取Wee模型对本文试验结果进行非线性回归分析,可建立应力-应变曲线形状特征参数k1、k2与钢渣骨料替代率及棱柱体抗压强度的函数关系,如式(11)、(12).
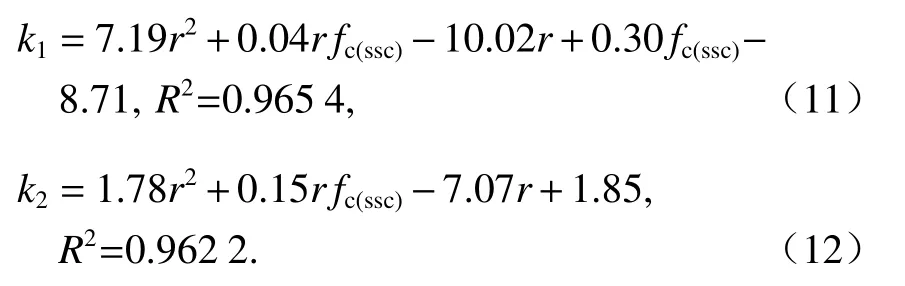
fc(ssc)的范围为[37.9,46.3],可将fc(ssc)近似成一个固定常数,以此得到k1、k2与r的关系,如图11所示,根据图11可知:在钢渣掺量60% ~ 70%时,钢渣混凝土下降段的脆性特征随钢渣掺量呈现不同的变化趋势.
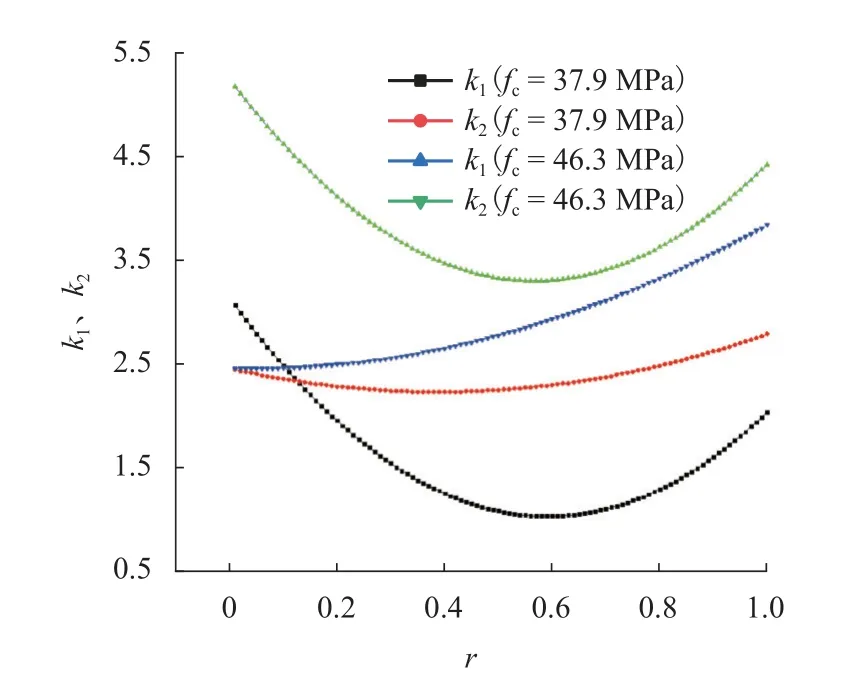
图11 下降段参数与替代率的关系Fig.11 Relationships between the descending parameters and the substitution rate
参照Wee模型,并考虑钢渣替代率的影响,对下降段参数 β 的公式进行回归分析,如式(13).
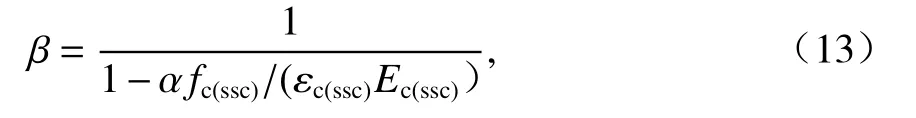
式中:α为拟合系数,与替代率的函数关系为 α=3.63r3−6.70r2+2.72r+0.78,R2=0.9409.
参数k1、k2、β与r、fc函数关系的确定系数均接近1,表明上述公式可较准确地反映不同替代率时钢渣骨料混凝土应力-应变关系中的参数值.由参数公式得到的模型曲线与试验曲线对比结果图12所示,可以看到,由以上参数表达的应力-应变关系模型与试验曲线基本吻合.
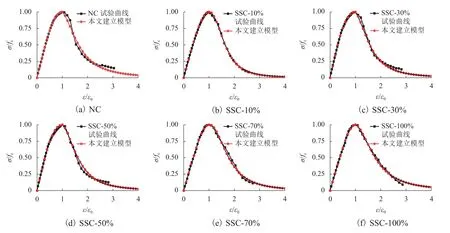
图12 试验曲线与本文建立模型曲线对比Fig.12 Comparison of test curves and model curves established in this paper
综上所述,本文提出的钢渣细骨料混凝土的本构模型可以很好地表达其单轴受压力学行为.
4 结束语
1)本文取用的包钢集团钢渣骨料的物理性能指标、钢渣中的游离氧化钙含量、压蒸粉化率均满足相关规范要求,适合作为混凝土细骨料.
2)利用不同地区的钢渣制备出的混凝土力学性能不尽相同,研究钢渣混凝土的强度及变形特征与替代率和基准混凝土的函数关系,进而将其体现在钢渣混凝土应力应变关系中,能够提高本构模型的适用性和可信度.
3)钢渣细骨料混凝土与普通混凝土的应力-应变关系曲线均具有上升段及下降段,但钢渣细骨料混凝土的上升段及下降段相对于普通混凝土均更为陡峭,且棱柱体抗压强度明显提高.本文建立了适用于钢渣细骨料混凝土的单轴受压本构模型,并提出了相应的参数公式.本文提出的钢渣细骨料混凝土的本构模型可以很好地表达其单轴受压力学行为.本文试件数量有限,得到的钢渣细骨料混凝土的本构模型尚需更多的试验予以检验.

