井位不确定环境下的油田仓库选址问题

潘雯雯, 郭海湘,2,3, 柯小玲, 顾明赟, 刘 晓

(1.中国地质大学 经济管理学院，湖北 武汉 430074; 2.中国地质大学 中国矿产资源战略与政策研究中心,湖北 武汉 430074; 3.西安财经大学 管理学院,陕西 西安 710100; 4.南昌大学 公共政策与管理学院,江苏 南昌 330031)

0 引言

石油在人们的日常生活和工业经济的发展中发挥着重要作用，国内石油消费量逐年增加，而国际原油价格逐年降低，这导致其利润空间不断缩小。因此，油田企业致力于提高油田生产运作效率；设施选址决策和网络布局决策属中长期决策[1～3]，影响油田的物流运输、管理成本甚至生产效率。油气田选址问题也被提出和解决：陈德泉[4]等1987年首次基于已知的油井个数和位置提出油田地面三级站选址问题，并设计剖分-选址两阶段方法优化油田计量站、转油站和脱水站选址问题，节约基建成本3%～5%。油库在油田物流中起着决定性的作用。吴勤旻[5]等基于油库选址问题提出考虑成本和非成本因素的二级优化方法。复杂的地形、地质特征、政府规划和工程建设也是影响油气田设施选址的重要因素：贾善坡[6]等从选址技术、地质安全、经济性和环境保护4个方面选取含水层储气库的选址指标进行选址分析。Daneshfar和Ardjmand[7]以距离城市最远、距离机场最近、地质准则等为原则，将油田垃圾(钻井岩屑)填埋场分为极好至极差的5个类别。由于油田油气运输一般采用管道运输，所以管道的建设直接影响油气输送效率，是油田选址布局不可忽视的部分。油气集输系统优化与油田设施选址既有相似之处，也共同影响油田工作效率。陈怀龙等[8]通过考虑井平台数和井深关系的井位优化数学规划模型确定油田井位部署方案。Wang等[9]分段处理非线性函数，并提出用最小化投资成本的混合整数规划模型求解油田集输管网和注水管网的布局问题，获得最优的设施位置、管道拓扑结构等。基于相互关系，管道铺设规划与油库选址决策也可同时进行。Nasab和Amin-Naseri[10]提出多周期、多层的油田物流集成方法，解决原油保存库的选址、库存和管道运输问题。Zarei和Amin-Naseri[11]通过考虑管道、设施的位置分配、管道路线及其容量、管道数量等因素，建立最小化总成本的天然气供应链节点优化混合整数规划模型。Hong等[12]考虑障碍物、三维地形、管道拓扑结构、管道直径、井口压力等相关操作和技术约束，构建了最小化施工总成本的混合整数线性规划模型，采用分段逼近技术和蚁群算法优化多周期气田集输管道系统，确定处理设施的位置、管道的安装和扩展。油井位置(简称井位)根据地下储层结构等因素决定，而且井位是油田设施选址的关键。Rodrigues[13]等提出了最小化开发成本的海上油田钻井平台整体选址0-1线性规划模型，解决钻井平台的数量、位置、容量和油井的数量、位置、类型。Al Dossary和Nasrabadi[14]提出最大化油气井产量的井位选址模型，并分析直井和水平井的井位。Silva和Guedes Soares[15]采用最小化投资成本的混合整数线性规划模型优化海上油田开发系统，确定开采平台和集合管的数量、容量、位置和油井分配关系。Alfares等[16]研究海上钻机选址优化问题，考虑钻井成本是关于钻机距离和钻机成本的函数，并将其最小化。Almedallah等[17]采用线性逼近约束优化和混合整数规划相结合的方法，实现了钻井井眼轨迹、平台位置、井眼配置和管网布局的优化，组合了三种管道连接方式。目前油田仓库选址问题的相关研究相对较少，现有研究：(1)油田非油井设施选址决策基于当前已知的井位，基本没有分析井位变化对决策的影响；(2)选址决策过程没考虑设施中断风险。而实际情况是：仓库未来服务的井位不固定，因此仓库选址时需要考虑未来井位的变化；油田作业要求仓库能持续为油井提供服务。在油气行业的勘探、开采过程中，都有此类需求存在。例如：中国石油化工股份有限公司华北分公司鄂尔多斯盆地南部(简称“鄂南”)油区，现有红河油田、泾河油田、渭北油田和洛河油田四个油田，勘探潜力巨大，是中石化华北分公司的重要石油开采区[18]；油区现有物资仓库无法继续使用，需要重新选址。

鄂南油区亟需建立服务于油田生产的新物资仓库，并且能在石油开采过程中持续地为油井工作提供物资。要求新仓库用于存储和配送四个油田生产所需物资。井位不确定和仓库中断风险是本文研究的重点和难点。所以，本文需要解决两个问题：(1)根据现存的油井分布和钻井规划(包括钻井数量和钻井区域)采用随机模拟方法来模拟未来井位，(2)建立考虑设施中断的仓库选址模型，并分析井位和物资需求量的变化对选址结果的影响。

1 模型与算法

1.1 问题背景

本文以鄂南仓库选址为背景：建立物资仓库，负责存储、配送四个油田的油井所需物资，以确保油井正常有序地工作。井位不确定：仓库的油井(包括评价井、开发井和存量井)；其中评价井是每年新钻的、用于评价地下储层含油性的井，开发井是每年新钻的产油井，均是钻井范围已知，具体位置未知；存量井是往年开发的产油井，其位置已知。油井数量已知：根据规划开放存量井或钻新井。所需物资量已知：新钻井所需物资量已进行测算。配送单价已知：每吨物资每公里需要0.8519元。由于井位将影响选址决策和运输费用，本文考虑先基于规划的油井数量和范围，使用随机模拟方法模拟井位，然后建立最小化运输费用和建库费用和的选址模型，最后进行灵敏度分析。

1.2 井位模拟

存在着不确定性的井位对于仓库选址决策有着决定性的影响；对于在决策过程中起关键作用的不确定性因素，可对其采用随机模拟的方法[19,20]。随机模拟方法在不确定决策中具有重要意义，大数定律和极限定理为该方法的使用提供了严密的理论支撑。所以，本文通过随机模拟生成井位，具体步骤如下：

图1 鄂尔多斯盆地南部油区坐标量化图

图1为鄂南油区的量化坐标图，从左至右的四个深色区域分别表示红河油田、泾河油田、渭北油田和洛河油田；红河油田中，虚线包围的区域为评价井钻井范围，实线包围的(标明年份的)区域为开发井钻井范围；泾河油田中也有两个评价井区域和五个开发井区域；渭北油田和洛河油田将不钻新井(评价井和开发井)。同时四个油田将会开放存量井。

第1步量化地图和油田坐标(见图1)，图中1个单位相当于实际距离1km。

第2步随机生成一个点A(即一对横、纵坐标)。

第3步判断点A是否在区域内，如果是，执行第4步；否则舍弃A，执行第2步。

第4步判断区域内的井数是否达到上限(即规划的钻井数量)，如果已达到，舍弃点A，执行第2步；否则将点A计入该区域，执行第5步。

第5步判断区域的钻井数是否均达到上限，如果是，执行第6步；否则执行第2步。

第6步随机选择一个存量井位B。

第7步判断井位B是否已选择，如果是，舍弃B并执行第6步；否则执行第8步。

第8步判断井位B所属油田的存量井数是否已达到上限(计划开放存量井的数量)，如果已达到，舍弃B并执行第6步；否则将开放B继续产油，执行第9步。

第9步判断存量井数是否均已达上限，如果是执行第10步；否则执行第6步。

第10步绘图。

1.3 仓库选址

仓库选址问题是在满足一定约束条件(如仓库容量约束、车辆容量约束、客户需求约束等)的情况下，以费用最小、距离最短等为优化目标，在合适的位置选择一个或几个位置建仓库并满足客户需求的问题。仓库选址是中长期决策，选址结果会长期、直接影响配送费用，据统计配送费用约占物流成本的50%；此外，选址决策也会影响油田管理工作。油田生产要求物资仓库能持续提供物资，所以仓库未来工作中面临的中断风险也是决策者要考虑的重要因素之一[21]。因此，本文考虑鄂南油区物资仓库的重要性、建库或租库的复杂性，基于物资仓库工作的正常场景和中断场景(物资仓库由于内部或外部原因无法为油井配送物资)，建立为了更清晰地描述仓库选址问题，做出以下说明：(1)一条路径只服务一个客户点；(2)无车辆数量限制。

I表示建库候选点的集合，fi表示第i个候选点每年的建设费用和消耗费用，Ci表示第i个候选仓库的容量；J表示所有待服务油井的集合，wj表示第j个油井的物资需求量；D={dij,∀i∈I,∀j∈J}表示任意建库候选点到油井的距离；K表示车辆类型的集合，Qk表示车辆的装载能力；A表示年份的集合；E表示所有场景的集合，其中包括正常场景和中断场景；pe和λe分别表示场景e发生的概率和增加的成本；c表示单位运输费用(单位为：元/(吨·公里))，u表示一趟空车返回的费用。

决策变量：

选址数学模型:

(1)

(8)

式(1)为目标函数，表示所有场景(仓库正常和中断的场景)费用的期望值最小；式(2)-(8)为约束条件：式(2)确保每个油井至少被服务一次；式(3)保证每个油井的车辆进出次数相等；式(4)确保油井由已开设的仓库负责配送物资；式(5)表示仓库容量约束；式(6)要求每个油井物资需求都被满足；式(7)和式(8)表示决策变量。

染色体编码应满足完备性、非冗余性、易读性原则。本文采用二进制(0-1)编码。现在假设：有m个候选点，需要从中选出n个作为仓库。基于该假设的染色体有m个基因位，其中基因位的值为1表示候选点被选中，0表示未被选中。本文遗传操作如下：

(1)选择操作：精英保留策略和轮盘赌方法。即首先选择一个适应度值最大的个体，进入下一代，然后通过轮盘赌方法在父代中随机选择popsize-1个个体进入下一代。

(2)交叉操作：交叉操作是确保种群多样性的主要方式，本文采用两点交叉策略。选两个染色体在第k1位至第k2位进行两点交叉，操作后得到两个不同于父代的新染色体。

(3)变异操作：变异操作是确保种群多样性的辅助方式，本文采用单点变异策略。对一个染色体的第k3位进行单点变异，得到一个新的子代染色体。

选址问题是NP难，当问题规模扩大，精确算法的求解时间会指数增长，影响决策的时效性。智能算法是解决NP难的常用方法，其中进化算法通过模拟物种进化的过程有效地优化决策问题。遗传算法是最经典的进化算法之一，具有灵活性强、全局搜索能力强、搜索速度快等优点，而且对求解选址问题有很好的效果[22,23]。本文采用遗传算法，步骤如下：

第1步读取数据、设置参数，如种群大小、最大迭代次数、交叉概率和变异概率。

第2步初始化种群，随机生成一个染色体A，若A满足约束条件，则将其放入种群中，否则舍弃；重复该步骤直至种群中的染色体个数达到种群大小，该种群记为chrom1。

第3步计算种群中每个染色体的目标函数值和适应度值。

第4步选择操作，首先采用精英保留策略选择1个染色体为chrom_best；然后采用轮盘赌策略选出popsize-1个染色体，生成新的子种群chrom_s。

第5步交叉操作，对chrom_s中的染色体进行两点交叉，产生新种群chrom_c。

第6步变异操作，对chrom_c中的染色体进行单点变异，产生新种群chrom_m。

第7步将chrom_best和chrom_m合并为一个新种群chrom2代替初始种群chrom1。

第8步判断是否满足约束条件，若满足，输出结果，否则返回第3步。

2 算例分析

2.1 算例描述

表1 各油田2016～2020年开井计划

表2 候选仓库的坐标、费用和容量

2.2 结果分析

根据图1的油田、规划钻井区域和表1的开井计划，采用随机模拟方法模拟出2016～2020年各个油区油井的位置，根据模拟结果统计出井位。然后采用遗传算法、结合上述数据，求解油田物资仓库选址模型，得出选址结果：选择3个(1、2和8号)仓库为油井服务，成本为1746.53万元。鄂南油区物资仓库的多种选址方案对比见表3：

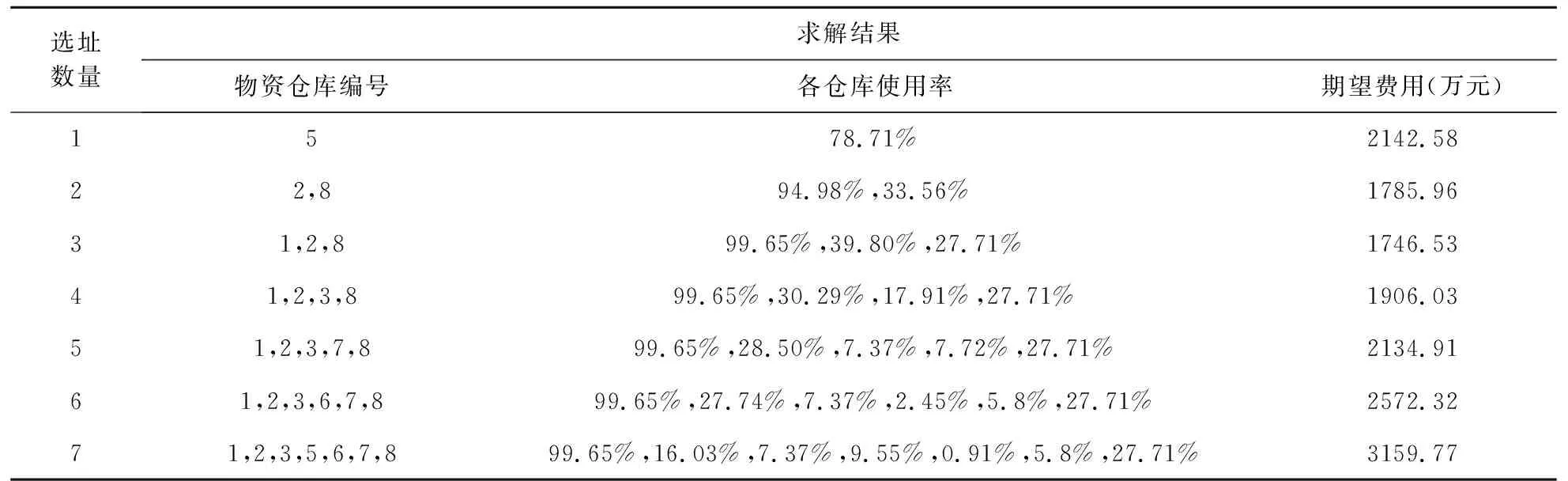
表3 选址结果对比表

3 灵敏度分析

选址问题是中长期决策，而油井的位置和需求量作为选址模型的输入参数，都存在不确定性，那井位和需求的变动是否会影响选址结果？如果是，将如何影响？所以本文从井位变化和需求量变化两方面对选址模型进行灵敏度分析。

3.1 井位变化

本文根据鄂南现有的油井分布和钻井计划对井位进行9次模拟，分别求解出对应的仓库选址结果，并与2.2的井位模拟和仓库选址结果进行比较，见表4。

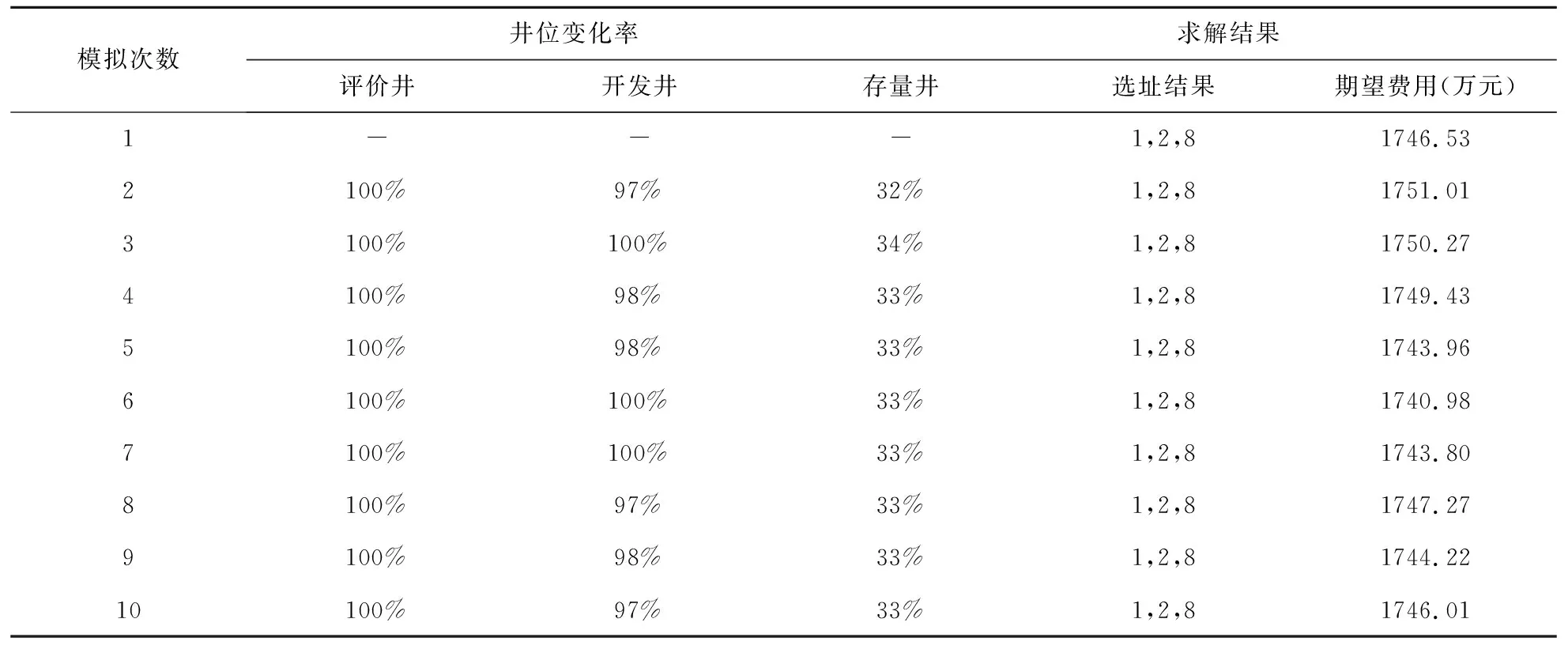
表4 基于不同井位的选址结果对比表

如表4：所有评价井的位置均不同于2.2部分，且至少97%的开发井和32%的存量井位置不同；得到的选址结果相同，费用不同，主要原因是由井位变化引起运输费用变化。

3.2 需求量变化

物资仓库服务的三种油井为开发井、评价井和存量井，其中开发井所需物资最多，20种主要物资共计263.4吨，评价井所需物资量为开发井的60%到100%，存量井约为10%到30%。为检验需求量的变化对选址的影响，本文基于需求量变化分析选址结果，见表5。

如表5，当评价井和存量井的物资需求量在正常范围内变化，1和2号候选仓库都会被选中。而且当评价井需求不变时，选址数量随存量井需求的增加而增加，费用随存量井物资需求的增加而增加；当存量井需求不变时，选址数量和选址结果不变(即评价井需求在正常范围内变化时不影响选址结果)，费用会随评价井物资需求的变化发生变化，但变化幅度较小，费用在1.3%的范围内浮动。所以，仓库选址决策可以首先确定1和2号候选仓库，其他候选仓库可根据物资需求量进行确定。鄂南油区物资仓库选址结果受存量井需求变化影响较大，而基本不受评价井物资需求变化影响。其原因在于：评价井数量较少，每年新钻8口；存量井数量大，每年计划至少开放240口。因此，在鄂南油区物资仓库选址需要考虑油井需求的变化，特别是存量井。综上所述，井位在钻井区域内变化将不影响仓库选址结果。存量井物资需求量的变化会影响选址结果；但是1和2号仓库被选中不受需求量变化的影响。

4 结论

本文研究了井位不确定环境下油田物资仓库选址问题。首先，考虑到仓库未来服务的井位的不确定性，根据油区现有油井分布和钻井计划采用随机模拟方法模拟未来井位；在此基础上，考虑油田物资仓库要持续为油井服务，应避免因仓库中断造成物资短缺，所以建立考虑设施中断的仓库选址模型；然后使用遗传算法求解选址模型得到油田物资仓库选址方案；以鄂南油区物资仓库选址为例，得到选址方案：当评价井物资需求为开发井的80%、存量井的物资需求为开发井的20%时，应从8个候选点中选取1、2和8号建立仓库，并着重避免2号仓库发生中断；最后，对选址决策进行灵敏度分析发现：在规划的钻井范围内，井位的变化对选址结果没有影响，只影响运输费用；选址结果受存量井物资需求量变化的影响较大。本文的选址研究内容对油田物流系统管理的研究具有一定的理论意义，研究结果对油田等行业的选址决策有重要的指导意义。本文在后续的研究中，将(1)结合已探明的地下储层结构和油田勘探规划；(2)参考油田钻井工作中，井位与井位间的位置关系进行油田仓库选址决策；(3)测算各物资候选仓库到油井的实际运输距离。