个性化推荐系统中协同过滤推荐算法优化研究

关 菲, 周 艺, 张 晗

(河北经贸大学 数学与统计学学院,河北 石家庄 050061)

0 引言

大数据时代下互联网的应用使人们的生活更加便捷与智能化。但随之而来的“信息过载”问题亟需解决，此时推荐系统应运而生。协同过滤[1]作为个性化推荐系统[2]中应用较为广泛的一种算法，因经常面临数据稀疏性和算法扩展性问题，近年来备受关注。因此，协同过滤算法的优化成为了国内外学者的研究热点。针对数据稀疏性问题，一些学者通过降维的方法来缓解稀疏性，比如文献[3]提出了基于矩阵分解的迭代最小二乘加权正则化协同过滤算法，对传统矩阵分解模型加入正则化约束以防止过拟合；文献[4]提出了基于矩阵分解和随机森林的多准则推荐算法；文献[5]利用自适应神经模糊推理系统，结合减法聚类和高阶奇异值分解提出了一种新的多准则协同过滤模型。还有一些学者通过矩阵填充来缓解数据稀疏性，比如文献[6]考虑了用户对项目的兴趣偏好，提出了一种结合用户兴趣偏好的矩阵填充方法；文献[7]通过非负约束下的低秩矩阵填充模型对矩阵缺失项取值进行预测。还有一些学者通过融合一些其他信息来缓解数据稀疏性带来的问题，比如文献[8～10]分别在推荐过程中融合了标签信息和时间效应、物品属性和用户间的社交联系、上下文对用户的影响以及项目的相关性等，均提高了推荐系统的准确性。针对算法扩展性问题，文献[11～13]分别采用了K-means聚类、二分K-means聚类、模糊K-means聚类先对物品进行聚类再推荐的方法，进而提高了推荐的精度和可扩展性；文献[14]提出了一种基于聚类矩阵近似的协同过滤推荐算法，通过对稠密矩阵块进行奇异值分解以及对各个稠密矩阵块奇异向量进行Schmidt正交来对原始评分矩阵进行重新近似；文献[15]将双聚类与协同过滤相结合，将双聚类的局部相似度和全局相似度结合在一起，构造了一个新的候选项目排名得分；分析上述文献可以看出：学者们大多采用降维、矩阵填充和融合其他信息的方法来缓解数据稀疏性。对于扩展性问题，学者们经常采用K-means聚类方法，然而K-means聚类存在一定的不足之处，可能会出现因聚类的用户簇不合理，从而导致推荐效果较差的现象。基于此，本文将从数据稀疏性和扩展性两个角度对协同过滤算法进行优化。

本文结构安排如下：第 1 部分介绍了本文所需用到的Slope One算法和基于K-means聚类的协同过滤推荐算法。第2部分提出了一种基于Slope One矩阵填充的协同过滤推荐优化算法。第3部分提出了一种基于中心聚集参数的改进K-means算法，并将该算法应用到协同过滤推荐中。第4部分，结论与研究展望，总结了本文算法的有效性并讨论了本文下一步的研究方向。

1 预备知识

1.1 Slope One算法

2005年，Daniel Lemire教授提出了Slope One算法[16]。其基本原理是计算不同物品间的一个评分差，用评分差预测最终用户对物品的评分。若将整个评分数据标记为R，主要分以下两步：

①在两个物品同时被评分的前提下，将两物品i、j的评分差取均值，记做评分偏差：

(1)

其中，rui和ruj表示用户u对项目i、j的评分，N(i)是对物品i评过分的用户，|N(i)∩N(j)|是对物品i、j都评过分的用户数。

②根据用户历史评分和由(1)得出的评分偏差，预测用户对没有做出过评分的物品的分值。

(2)

1.2 基于K-means聚类的协同过滤推荐算法

设X={xi|xi∈Rp,i=1,2,…,n}为原数据集，每个数据由用户、项目、评分3部分组成。设目标用户为u，用户集合是U={u1,u2,…,um}，K-means聚类得出的用户集合可以表示为U={C1,C2,…,Ck}，k为聚类个数。算法步骤[17]如下：

(1)在X中随机选出个样本作为初始簇心Mi(i=1,2,…,k)；

(2)用初始簇心Mi(i=1,2,…,k)对用户-项目评分矩阵Rm×n执行经典K-means算法，得到k个类；

(3)使用欧氏距离计算目标用户u与k个簇心间的距离，根据最小距离，找到u所属的类别；

(4)在u所属类中，计算u与其他用户的相似性，获取u的最近邻居集Nuj(j=1,2,…,m)；

(5)得到最近邻居集后，预测求得想要推荐给u的项目的评分，由高到低排序后，把前N个项目推荐给u。

2 基于Slope One的协同过滤推荐优化算法

为有效缓解数据稀疏性，本节中我们选取MovieLens 100k数据集，数据集详情如表1。

表1 MovieLens100k数据集基本信息

(实验环境为Windows 8系统；硬件条件为CPU2.3GHZ，4G内存，100G；使用软件Python 3.7版本)我们选取9种不同方法进行稀疏矩阵的填充，并选用均方根误差(RMSE)来判定有效性。

参照文献[18]，我们用全局均值法、用户平均法、物品平均法、用户活跃度&物品不平均、用户活跃度&物品平均、用户不平均&物品流行度、用户平均&物品流行度、用户活跃度&物品流行度、Slope One这9种不同方法进行填充，其均方根误差见表2。

从表2的结果可以看出，当使用Slope One方法进行填充时，其RMSE是最小的，说明使用该方法填充时误差较小。下面我们将采用Slope One方法对MovieLens 100k版本数据集进行填充，结果见表3。

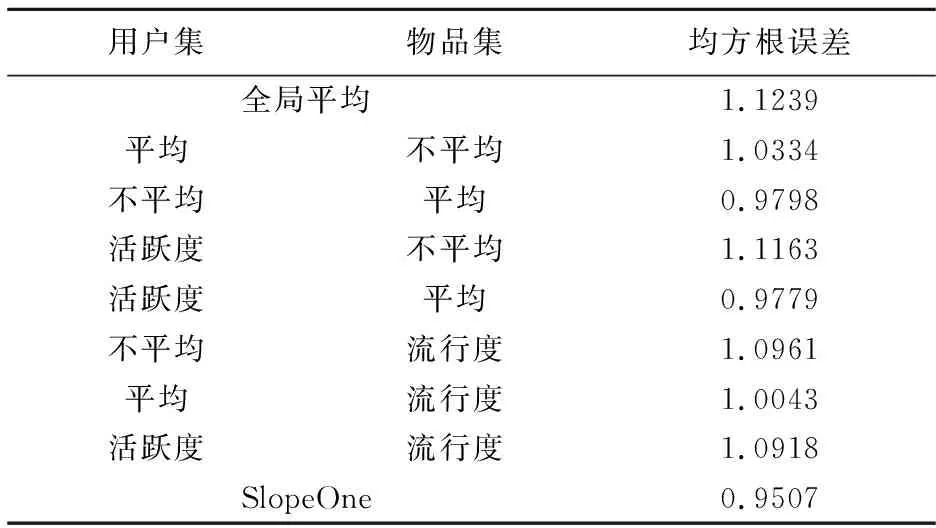
表2 MovieLens数据集上不同填充方法的均方根误差

由表3可知，进行了矩阵填充后，数据集的稀疏度变为6.37%，说明运用Slope One填充的效果明显。我们使用填充后数据设计了两组对比实验，以验证有效性：

实验1确定最佳聚类个数。在这一阶段的实验中，分别利用由Slope One填充前和填充后的数据，得到两个最佳K-means聚类个数。在确定过程中，我们选取平均绝对误差(MAE)作为测量标准，当聚类个数以2为间隔，由2增加到20时，根据MAE的大小来确定出最佳聚类个数，为了保证推荐时选取的近邻数相同，将其固定为25，以此增强MAE值的可靠性。图1中纵坐标代表MAE值，横坐标是聚类个数。

表3 用Slope One填充后MovieLens100k信息表

实验结果表明：图1中随着聚类个数从2增加到20，在进行SlopeOne填充和未填充时，K-means不同聚类个数的MAE值都呈现出先下降后上升的趋势，且波动幅度较小。两种情况的MAE最低值都出现在k=8，因此最佳的聚类个数都是8。

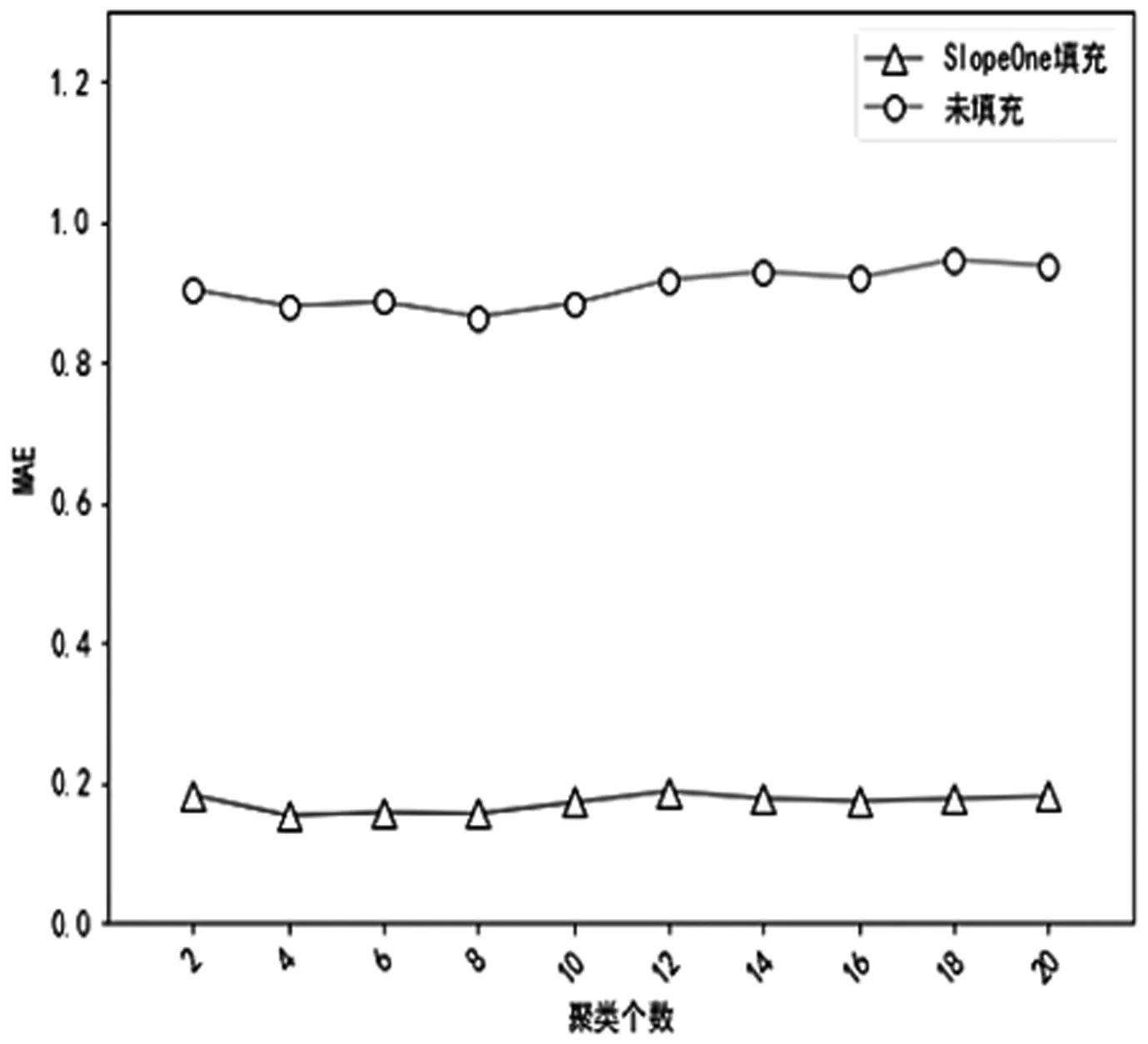
图1 K-means算法不同聚类个数的MAE变化对比图

实验2推荐算法精度对比。我们采用三种算法来做对比试验，分别是：基于SlopeOne填充后的K-means协同过滤推荐、经典K-means协同过滤推荐和传统的协同过滤推荐算法。图2中纵轴是MAE值，横轴是近邻个数，以5为间隔从5增加到50，结果如图2所示。

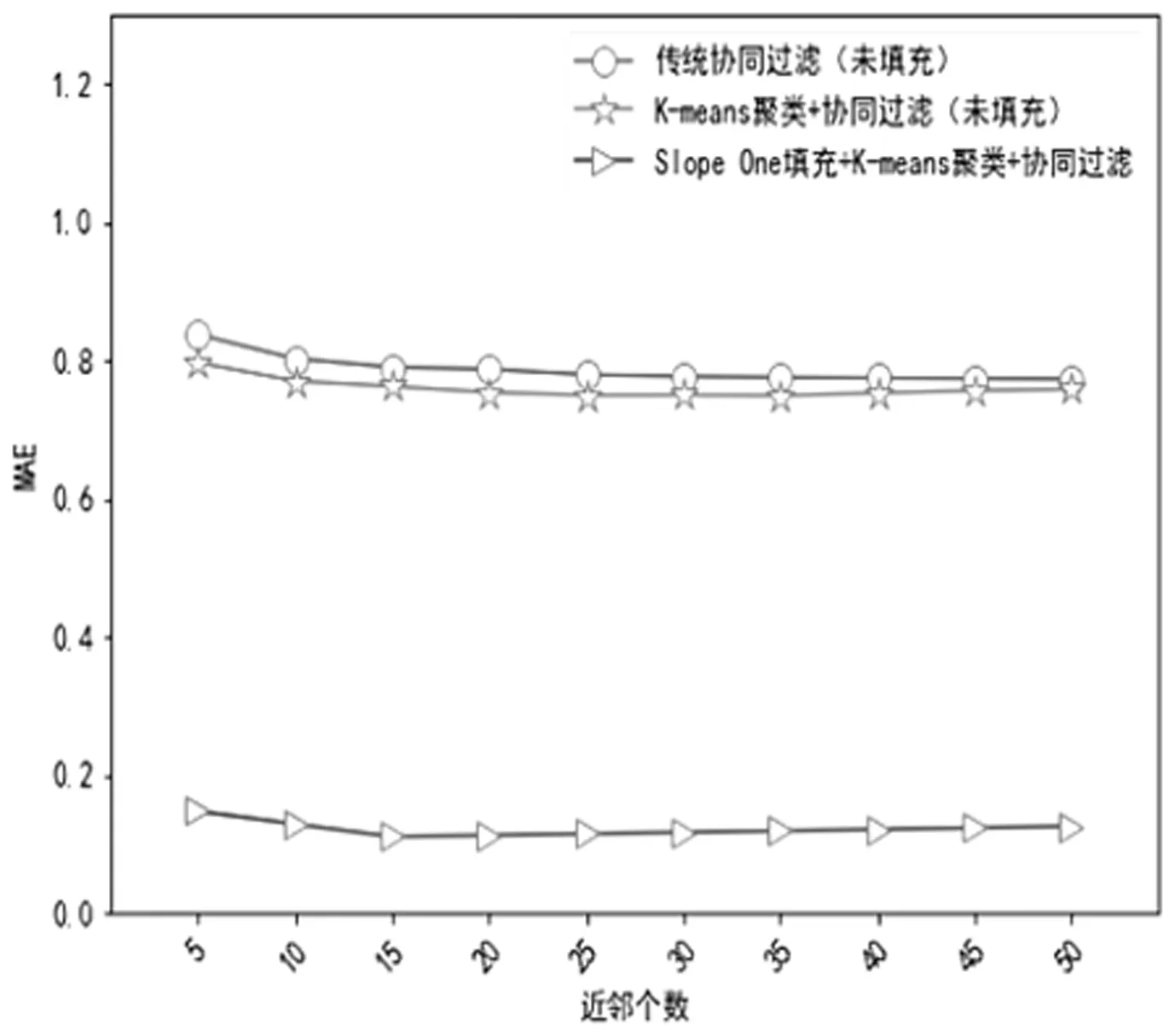
图2 不同近邻个数MAE值对比

由图2可以看出，三种协同过滤推荐算法的MAE值都随着最近邻个数的增加呈现出缓慢下降的趋势，且在邻居个数变化相同时，用Slope One填充后的K-means聚类协同过滤算法的MAE值最小。因此，在推荐之前，先对评分矩阵进行填充，这样能增加一些用户评分数据，以便在推荐过程中发掘出更多的可供推荐的项目，填充完毕的矩阵再对用户进行K-means聚类，这样是为了能缩小近邻寻找范围，类中的所有用户相比类外的用户与目标用户具有更高的相似程度，在后续的近邻匹配选取时也就更便利。

3 基于改进K-means的协同过滤推荐优化算法

3.1 基于中心聚集参数的改进K-means算法

由于第2节中用到的传统K-means聚类算法的初始中心和聚类个数k均是随机产生的，其合理性会影响聚类结果。因此，本节中我们参考文献[19]，首先给出如下定义：

定义1任意两个数据点间距离的平均值为:

(3)

其中，d(xi,xj)是任意两点之间的欧式距离，n表示数据点的个数。

定义2定义邻域半径R为:

(4)

releR是一个用来调节的系数，releR取0.13时，聚类效果最好。

定义3点的聚集度定义:

(5)

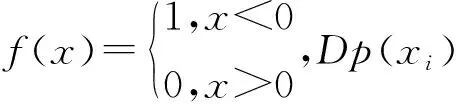
定义4簇类平均距离定义为:

(6)

簇类平均距离Gavgd(xi)衡量的是元素密集度，数值越小，说明在目标用户xi所在类中，数据点之间越紧凑。

定义5聚集度距离G(xi)定义为:

(7)

G(xi)是通过比较聚集度Dp(xi)来确定的，用它来衡量不同簇之间的差异性。在所有的点中，当xi的聚集度最大时，G(xi)是xi与剩余所有点之间的最大距离，反之则为xi与剩余所有点之间的最小距离。

定义6中心聚集参数定义为:

(8)

基于以上概念，我们给出基于中心聚集参数的改进K-means算法流程：

输入：所有的数据集点x1,x2,…,xn

输出：聚类结果

(1)计算出每个点的中心聚集参数ω(xi)；

(2)选出使得ω(xi)最大的点xi，由它做为第一个初始聚类中心，计算出xi与剩余点间的距离，将得到的距离值与邻域半径R作比较，若距离小于R则说明可以与xi划为一类，因此将从数据点中除去这些点，若距离大于R，则说明与xi的距离过远，不适宜与xi归为一类，因此将这些点保留下来，进行下一步；

(3)在第(2)步中保留下的点里再选出ω(xi)最大的点，作为第2个聚类中心，再次操作步骤(2)；

(4) 一直重复操作步骤(3)，当数据集中的点x1，x2，…，xn全部去除为止；

(5)输出k个最优初始中心Mi(i=1,2,…,k);

(6)利用初始簇心Mi，对Rm×n执行K-means算法，将数据集分成k类；循环执行K-means算法，直至其准则函数收敛，得到最终聚类结果；

为验证上述算法的有效性，我们选取以下UCI数据集进行验证(见表4)，同时选取的评价标准有：调整后的兰德指数(RI)、互信息(MI)以及Fowlkes-Mallows指标[19]。实验结果如图3～图5：

表4 UCI数据集

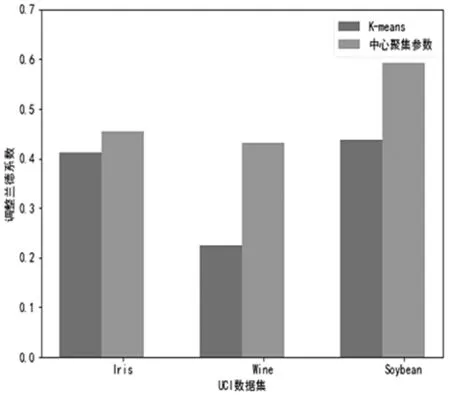
图3 调整兰德指数指标对比

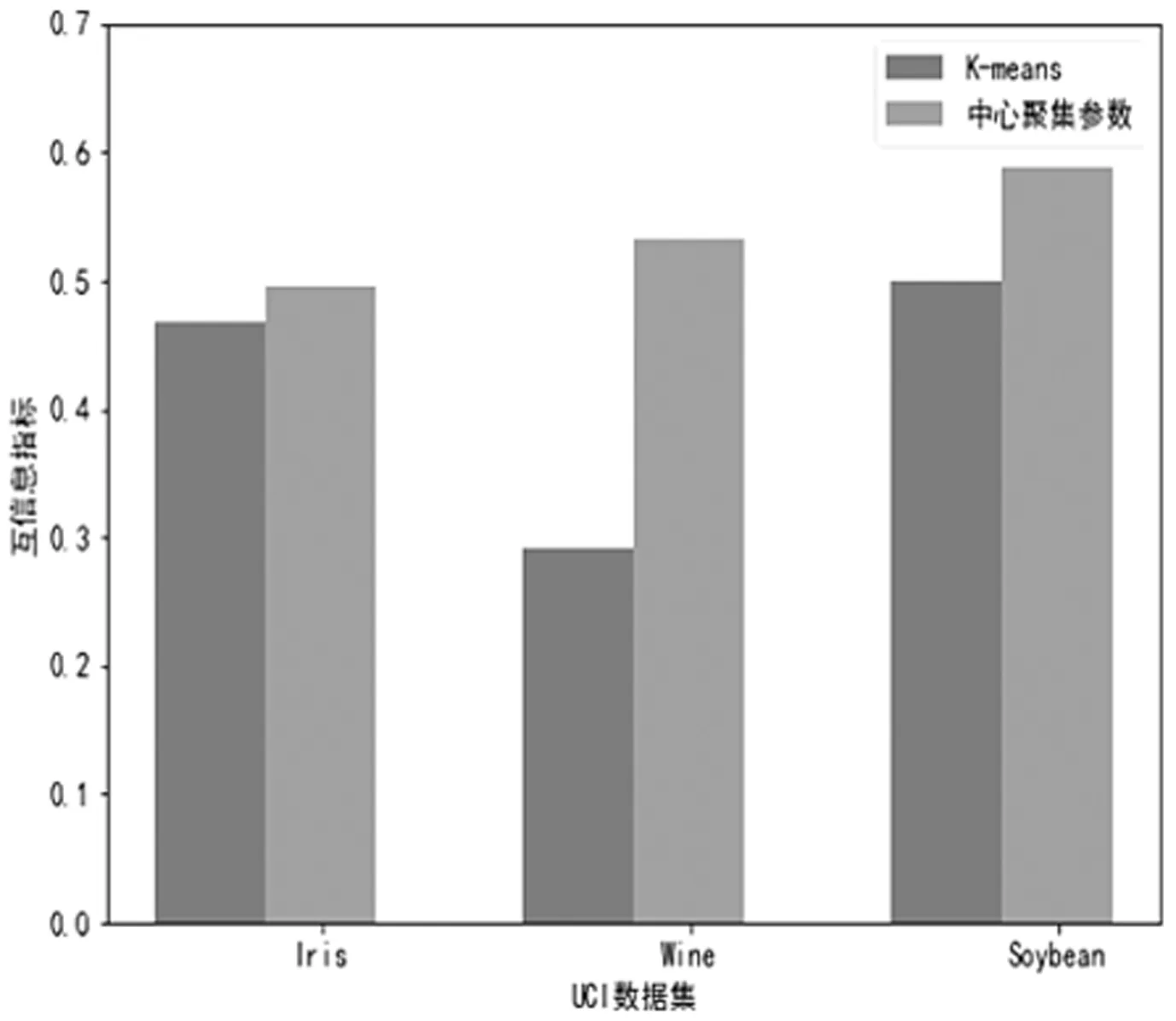
图4 互信息指标对比

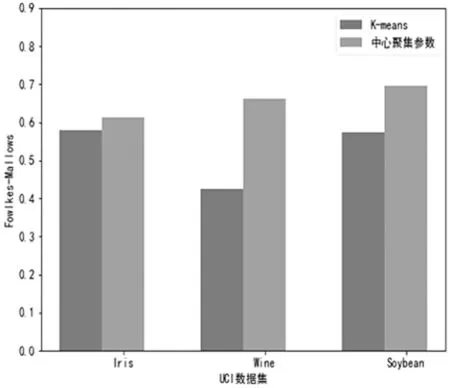
图5 Fowlkes-Mallows指标对比

由图3、图4和图5，我们可以看出基于中心聚集参数的改进K-means算法得到的相关数值均比经典K-means聚类算法值要高，并且在Wine和Soybean两个数据集上的表现更为明显。因此通过此实验表明，基于中心聚集参数的改进K-means算法具有较好的聚类效果。

3.2 基于中心聚集参数的改进K-means协同过滤推荐算法

本节中，我们把3.1节中基于中心聚集参数的改进K-means算法用于协同过滤推荐过程中，为验证改进后的算法在推荐上的效果，为方便起见，我们从MovieLens100k数据中随机选取了189名用户的评分数据，并按2:8分为测试集和训练集，设计了如下两组对比实验：

实验1确定最佳聚类个数。在这一阶段的实验中，需要得到两个最佳聚类个数。首先执行基于中心聚集参数的改进K-means算法，得出最佳的聚类个数是19；其次需要判定经典K-means算法的最佳聚类个数，选取的评价指标是平均绝对误差(MAE)，当聚类个数以2为间隔，由2增加到20时，根据MAE的大小来确定出最佳聚类个数，为了保证推荐时选取的近邻数相同，将其固定为25，以此增强MAE值的可靠性。

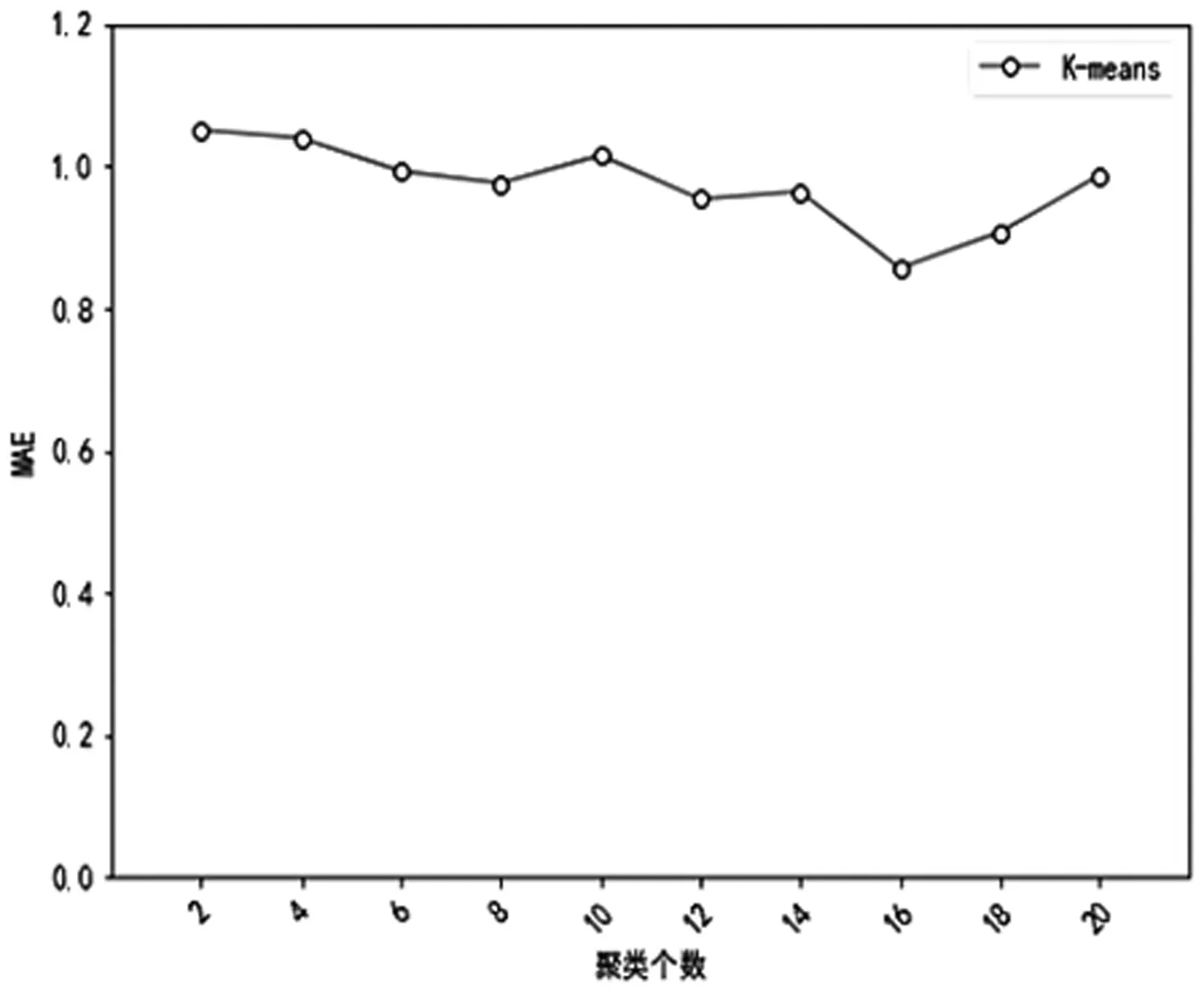
图6 经典K-means不同聚类个数下的MAE变化

图6表明：随着聚类个数的增加，MAE值呈先下降后上升趋势，在聚类数k=16时最低。因此对经典K-means算法而言，最佳聚类个数是16，从而保证获取有效的分组，提高在近邻选择时的便利性和可靠性，取得较好的推荐效果。

实验2推荐算法精度对比。我们采用三种算法来做对比试验，分别是：基于中心聚集参数的改进K-means协同过滤推荐算法、基于K-means的协同过滤算法与传统的协同过滤推荐算法。下图中纵轴是MAE值，横轴是近邻个数，以5为间隔从5增加到50。

由图7可以看出，进行对比的三种协同过滤推荐算法它们的MAE值都呈现先下降后上升的趋势，整体上随着最近邻个数的增加而降低，且在同样的邻居个数变化的前提下，基于中心聚集参数改进K-means协同过滤推荐算法的MAE值最低。MAE值越低表明推荐误差越小，所以当目标用户的近邻数不断增加时，推荐准确度也随之提高。因此，基于中心聚集参数的改进K-means协同过滤推荐算法的推荐效果较好。

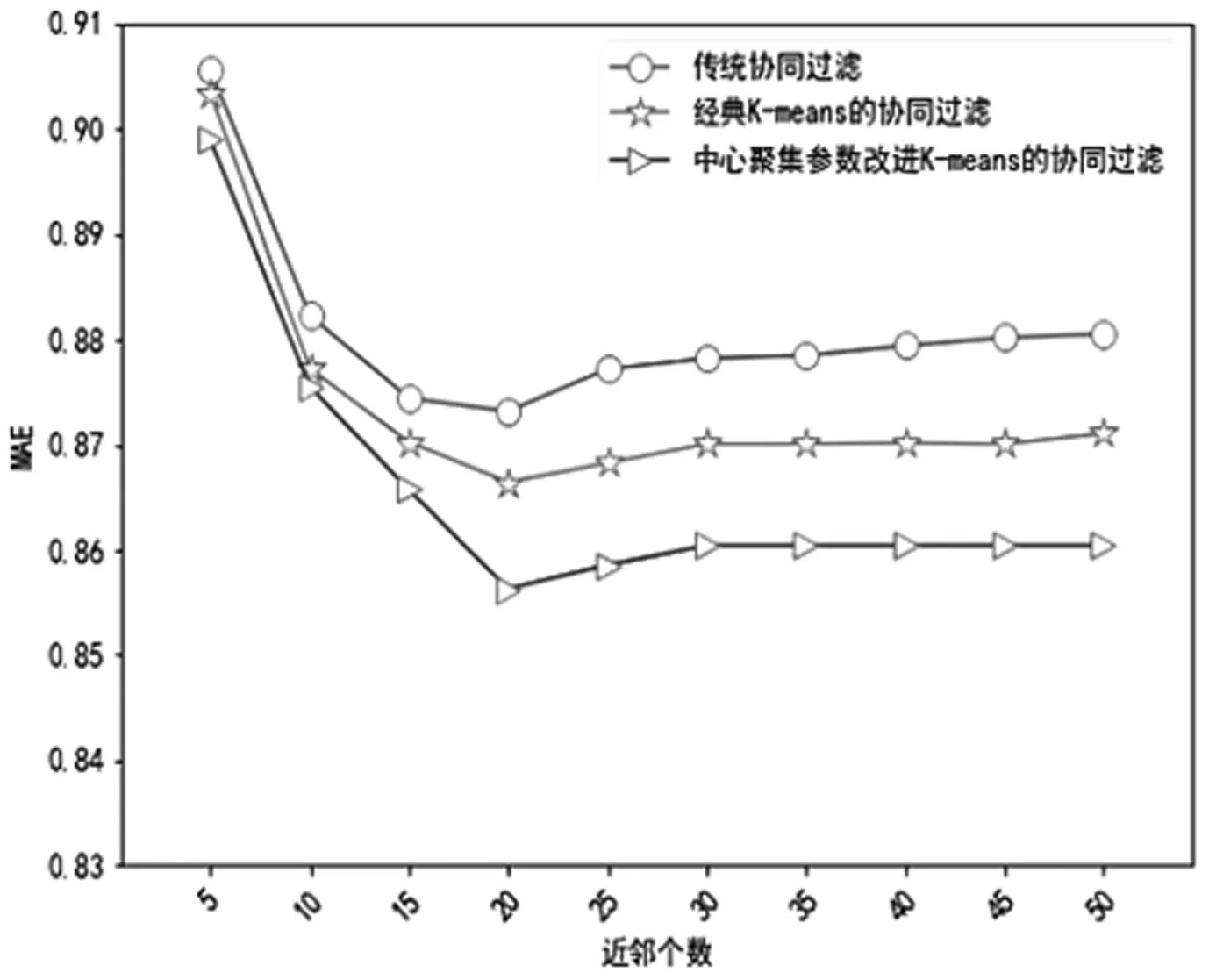
图7 不同近邻个数下MAE变化

4 结论及展望

本文主要从两个角度对个性化推荐系统中的协同过滤推荐算法进行了优化。首先，基于Slope One算法对缺失数据进行填充，提出了基于Slope One的协同过滤推荐优化算法。其次，提出了一种基于中心聚集参数的改进K-means优化算法，并将该算法用于协同过滤推荐中。为验证本文提出算法的有效性，结合MovieLens数据集设计了相应的对比实验，结果表明：本文所提方法推荐精度均得到显著提高，数据稀疏性和扩展性问题得到了一定程度的改善。但本文仍有一定不足之处，比如第3节中因用Slope One填充后的矩阵过于庞大，未能将Slope One填充与基于中心聚集参数的协同过滤推荐算法相结合，这将是本文后续工作中需要解决的重要问题。