用非均匀团聚体模型模拟燃料电池老化过程
杜新,范进伟,郭丽君,王金龙
(1 长春理工大学机电工程学院,吉林 长春 130022;2 长春理工大学物理学院,吉林 长春 130022)
质子交换膜燃料电池(proton exchange membrane fuel cell,PEMFC)具有效率高、工作温度低、能量密度大、环境友好等优点,在航空航天、电动车辆、电器等领域具有广阔的应用前景[1]。目前,PEMFC在性能、寿命和成本方面离大规模商用的要求还有差距,特别是耐久性方面,国内外差距较大[2]。建立更准确的催化层模型有助于理解燃料电池老化的演化规律,具有重要的研究意义。
早期的催化层模型被看作是质子交换膜和气体扩散层之间的界面。Bernardi 等[3]和Springer 等[4]建立一维模型,研究了燃料电池内物质传输现象,如水通过聚合物膜的传输和气体在电极中的扩散。之后,均质分布的催化层模型被提出,Marr 等[5]分析了燃料电池阴极催化层的结构与性能的关系,得到了最佳催化层孔隙率和Pt 负载量。目前,均匀分布的团聚体模型被广泛采用。团聚体是一种多尺度模型,质子、氧气等反应物质通过气体扩散层和质子交换膜来到催化层,再在团聚体内催化剂表面发生电化学反应产生水和电子。Sun 等[6]推导了球型团聚体模型的解析解,研究团聚体对催化层反应的影响。Xing 等[7]建立了二维稳态等温模型,研究了孔隙率、铂/碳负载量等参数对燃料电池性能和效率的影响。Zhang 等[8]建立了耦合尺度模型和空隙尺度模型,优化电解质相的含量,在提高燃料电池性能的同时减少铂负载量。Zhang 等[9]建立了三维两相微观结构晶格模型,研究了PEMFC 内团聚体对催化剂利用率、迂曲度和燃料电池性能的影响。皇甫宜耿等[10]建立了PEMFC 动态模型,分析了在负载突变的情况下输出电压的动态响应特性。
目前的研究多针对均匀分布的团聚体。但大量研究表明,载体、离聚物以及分散催化剂多为无序分布。并且在燃料电池老化过程中,催化剂发生迁移和溶解,其团聚程度决定了催化层的物理化学性能[2]。Zhao 等[11]通过单电池循环伏安实验,用电子透射显微镜观察膜电极,在质子交换膜中发现了溶解再沉积的铂颗粒。此外,燃料电池在工作时,电极内的氧气浓度、氢气浓度、含水量和温度等都存在不均匀分布的情况,具有梯度结构的催化层可能会提高燃料电池的性能[12]。Kamarajugadda等[13]研究了团聚体重叠模型对燃料电池整体性能的影响。Qi等[14]通过能量最小构型重建了催化层的微结构模型,用格子玻尔兹曼法模拟了孔隙率、重叠率和粒子形状对聚合物电解质膜除湿器性能的影响。
本文用有限元法建立了包括催化层、气体扩散层的宏观电极模型和催化层内团聚体的亚尺度反应模型,通过拉伸变换,建立两种尺度模型的传质关系。然后通过催化剂在团聚体的分层分布及其在催化层厚度方向的连续分布,研究催化层的不均匀性对燃料电池性能的影响规律。
1 数学模型
相比阳极侧的氢氧化反应,阴极侧的氧还原反应速率慢,对燃料电池性能影响更大,因此只研究阴极一侧反应。考虑双极板上流道分布具有周期性,选取1 个周期结构分析,二维电极模型如图1所示,包括气体扩散层(gas diffusion layer,GDL)、催化层(catalyst layer,CL)。其中,AG边是双极板上流道和GDL 的界面,GB边是双极板上肋板和GDL 的边界,AE和BF边给定对称边界条件,EF边为CL 和质子交换膜(proton exchange membrane,PEM)的边界。空气通过AG边从流道进入GDL 和CL,质子通过EF边进入CL,两者在CL内发生电化学反应。

图1 阴极模型
阴极气体扩散使用Maxwell-Stefan方程[式(1)]来描述。
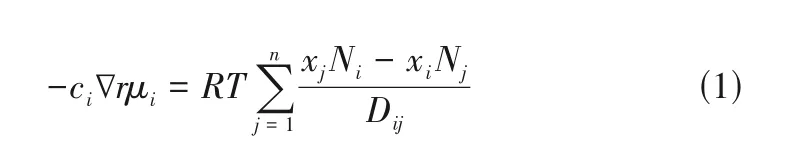
式中,组分i分别是氧气、氮气和水蒸气;ci∇rμi为作用在单位体积混合物中组分i上的力;R为气体摩尔常数,J/(moL·K);T为工作温度,℃;Dij为有效扩散系数,m2/s;x为摩尔分数;N为摩尔通量。其中,Dij可用式(2)计算。

在气体扩散层和催化层中,分别有孔隙率ε=εGDL或εCL。
在催化层,使用三维结构模拟团聚体作用,如图2所示。其中团聚体内,xy平面与电极模型中的催化层部分一一对应,z方向代表团聚体的半径方向。气体扩散仍用式(1)描述,电化学反应用Butler-Volmer方程[式(3)]描述。



图2 电极模型和团聚体模型的质量耦合关系
电荷传输遵守欧姆定律[式(4)]。

对于质子,k=keff为有效质子电导率,S/m,∇ϕlocal=∇ϕl,local为局部电解质电势差。对于电子,k=keffs为电子电导率,S/m;∇ϕlocal=∇ϕs,local为局部电势差。
那么,总书记为何提出“要加强对权力运行的制约和监督”?这当然不是说以往我们对权力的运行没有制约和监督,而是指这种制约和监督还“不强”,或“不太强”,还没有真正把“权力关进制度的笼子里”。因此,值得我们认真思考和琢磨的问题应当是:权力为什么需要“关进制度的笼子”?约束权力之“制度之笼”由谁来编织以及怎样编织才真正有效和管用?等等。
模型耦合建立上述两种尺度模型之间的传质关系。电极模型为二维模型,而团聚体模型为三维模型,z方向代表团聚体的半径方向。为和球坐标系表达一致,z方向的扩散系数和电导率分别修改为式(5)、式(6)。

式中,ragg为团聚体半径。
关于团聚体表面(z=ragg)氧气浓度c(O2)|ragg,设其等于电极模型催化层内氧气浓度。
关于宏观电极模型中的质量源项Ri,由团聚体模型中的反应气体通量[式(7)]给出。

式中,Mi为反应气体的摩尔质量,kg/mol;av为催化层中有效比表面积,m-1;Ni|ragg为团聚体表面的反应气体通量,mol/(m2·s)。因为流入团聚体的氧气流量全部在催化剂表面反应掉,对均匀分布的团聚体模型则有式(8)。

2 验证和结果分析
2.1 模型验证
本文使用工程有限元软件COMSOL 进行仿真,其燃料电池模块可以方便地引入质量、电荷传输和电化学反应。首先,用均匀团聚体模型,通过改变电池输出电压(=平衡电势-过电势)计算平均电流密度,得到燃料电池的极化曲线。仿真所需几何、物理参数和工况来自Yan等[15]的实验数据。团聚体模型所需团聚体参数,如团聚体半径、催化层厚度等来自Xing等[7]的团聚体解析解模型。仿真结果如图3 所示,同时加入团聚体的解析解模型[7]作为比较。可以看到,仿真结果和实验数据、解析解模型的结果基本一致;在高电流密度下,和解析解相比,数值解和实验结果更加符合。

图3 模拟结果和实验数据的对比
2.2 催化层中电流密度分布
图4是过电势为0.4V时催化层中电解质电流密度分布的等值线图,上侧边界是催化层和气体扩散层间的界面,下侧边界表示与质子交换膜的界面。从图4中可以看出,催化层在靠近气体扩散层一侧的电解质电流密度最小,靠近质子交换膜一侧最大。根据图4,沿x轴方向做积分,得到质子平均电流密度沿膜厚方向的分布情况,如图5所示。横坐标是距离GDL 的相对深度。在GDL 界面,质子电流密度最小。在催化层厚度前40%左右急剧升高,此后缓慢增加,在PEM 界面达到最大,其变化趋势和文献[5]中的结果一致。
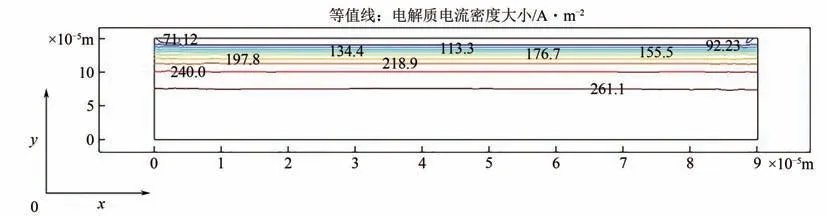
图4 电解质电流密度

图5 电流密度沿催化层厚度的分布
2.3 团聚体内催化剂分层分布
如文献[11]所述,燃料电池老化过程中发生催化剂颗粒迁移。本文使用分层团聚体模型进行模拟。假设了两种分层模型:第1种情况,催化剂颗粒首先从团聚体表面流失,团聚体内部的催化剂保持不变,如图6(a)所示;第2 种情况,假设催化剂在团聚体内均匀地由内向外迁移,如图6(b)所示。图中,黑色区域是有催化剂区域,白色区域没有催化剂,表示催化剂颗粒流出团聚体。
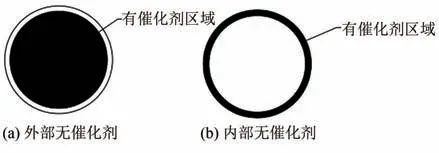
图6 团聚体内催化剂分布



通过图7 和图8 的极化曲线的对比,可以看出,团聚体外部区域的催化剂流失对燃料电池性能的影响大得多。但根据文献[11]中的不同电位循环的极化曲线结果可以发现,燃料电池性能下降是缓慢发生的,因此第2种模型,即催化剂在团聚体内呈现出整体运动趋势的假设更合理一些。

图7 燃料电池的极化曲线

图8 燃料电池的极化曲线
2.4 团聚体分层连续变化模型
燃料电池老化,催化剂颗粒不断离开原有位置,溶解、再沉积,空间分布呈现连续变化。催化剂不仅在团聚体内分布不均匀,而且在整个催化层内分布也不均匀。
假设团聚体尺寸不变,但分层界面在CL 内与空间位置相关。模型的基本条件和参数不变。对于团聚体中催化剂沿膜厚方向分布,可分为均匀不分层、均匀分层、分层递增和分层递减分布4 种模型。分层模型均采用上述第2种情况,即团聚体内部无催化剂的情况。
递增型是分层界面从球心到表面呈线性增加分布,模拟催化剂向PEM 方向迁移,在靠近气体扩散层一侧的团聚体内无催化剂,在靠近质子交换膜一侧的团聚体内催化剂均匀分布。递减型是分层界面从表面到球心呈线性减少分布,模拟催化剂向GDL 方向迁移,在靠近气体扩散层一侧的团聚体内催化剂均匀分布,在靠近质子交换膜一侧的团聚体内无催化剂。

假设催化剂迁移过程中团聚体内催化剂密度不变。仿真时改变燃料电池的电位,通过计算求出平均电流密度,绘制燃料电池的极化曲线。结果如图10 所示,在燃料电池电位大于0.8V 时,递增分布的燃料电池和均匀分布的燃料电池性能接近,分层分布的燃料电池性能有所下降,递减分布的燃料电池性能最差;当电位小于0.8V 时,递增分布燃料电池的电流密度是均匀分布的60%左右,分层分布燃料电池的电流密度是均匀分布的32%左右,递减分布的电流密度是均匀分布的10%左右。从模型的几何区域已知,递增分布和递减分布模型的催化剂的分布体积都是均匀分布模型的一半,但由于靠近PEM 处电解质电流密度大,递减分布模型对燃料电池性能影响更大,即催化剂向GDL 方向迁移有更大的影响。从极化曲线图10 可以看出,在催化剂的分布体积相同时,递增分布燃料电池的性能>分层分布燃料电池的性能>递减分布燃料电池的性能,从而可以推断出靠近质子交换膜一侧催化层的催化剂利用率较高。
在催化剂迁移过程中,铂负载量(mPt)在团聚体内也可能发生改变。假设铂催化剂未流出催化层,只是向两侧聚集。由图9可知,递增分布和递减分布模型的反应体积都是均匀分布模型的一半,相当于对应模型的铂负载量增加一倍。对比图10和图11发现,铂负载量增加1倍对递增分布模型和分层分布模型都有所提高,当输出电压是0.2V时,电流密度分别提高了21%和9%左右。和均匀分布模型对比,催化剂总量不变,但是由于催化剂分布不均匀造成燃料电池性能下降。对递减分布模型,铂负载量的改变对燃料电池的性能基本没影响。这是由于电化学主要发生在催化层靠近质子交换膜的区域,而递减分布模型的铂主要分布在催化层的另一侧。通过分层递增和分层递减模型以及铂负载量的改变,可以说明在靠近质子交换膜一侧铂分布对燃料电池性能的影响最主要。

图9 铂在微观组件中的分布区域

图10 燃料电池极化曲线(mPt不变)

图11 燃料电池极化曲线(mPt增加一倍)
3 结论
通过分层团聚体模型,研究了燃料电池老化过程中不均匀催化层对燃料电池性能的影响,主要结论如下。
(1)质子电流密度在催化层的分布表明,电化学反应主要发生在催化层靠近质子交换膜的区域。

(3)团聚体内分层界面沿膜厚方向线性改变的仿真结果表明,递减分布模型比递增分布模型对燃料电池性能的影响大,相比向PEM 方向迁移,催化剂向GDL 方向迁移对燃料电池性能有更大的影响;此外,铂负载量的改变对递增分布模型的电池性能有所提高。

