基于短时峭度法的钢丝绳损伤检测及定位研究

刘 添，黄升平，田丰，沈萌恩

1中国矿业大学机电工程学院 江苏徐州 221116

2江苏省矿山机电装备重点实验室 江苏徐州 221116

作 为矿井提升机的关键零部件，钢丝绳由高强度的钢丝编绕制成，具有抗拉强度高，自重轻，柔韧性能好等特点。同时，钢丝绳也是工业中极其重要的挠性承载元件之一[1]。钢丝绳的无损检测同样具有重要意义，如可防止断绳事故的发生，有效延长钢丝绳的服役时长等[2]。在矿业生产中，我国劳动部印发的《中华人民共和国矿山安全法》中明确列出钢丝绳作为重点关注对象。虽然钢丝绳不易骤然整根折断，且工作可靠，但是在矿井等恶劣工况下长期工作，也会出现各种损伤，如断丝、磨损、锈蚀、变形等[3]。而且，钢丝绳损伤还会随着工作时间的增加而日益严重，甚至引起设备停机等灾难性事故，造成巨大损失[4]。

钢丝绳结构的复杂性、工作环境的多样性以及检测方法的局限性使得钢丝绳缺陷检测非常困难[5]。目前，钢丝绳无损检测的方法包括光学检测、磁检测和射线检测等。在多种无损检测方法中，电磁检测法因为成本低、易于实现等优点被广泛应用。钢丝绳的漏磁信号在空间域是非平稳的，通过检测信号的异常冲击来确定缺陷，其频域特征很少。因此，使用传统的滤波方法或傅里叶变换无法确定缺陷的类型、位置和范围。近年来，随着计算机技术和数字信息处理科学的飞速发展，各种漏磁检测方法被提出。Gao 等人[6]提出了基于小波的钢丝绳故障诊断，通过设定阈值的方式对钢丝绳的缺陷进行判定，但是阈值的设定需要依靠检测者自身的先验知识。李兆星等人[7]采用集合经验模态分解对采集的信号进行降噪处理，并结合所提出的筛选 IMF 分量的方法，通过磁记忆信号法向分量特征曲线对损伤进行识别。钟小勇等人[8]通过软硬件结合的方式，提高采集数据的信噪比，并剔除了股波干扰来提高对钢丝绳损伤识别的准确度。Liu 等人[9]利用缺陷滤波和小波去噪的方法消除了信号中的股波信号，实现对缺陷信号的检测。窦连城等人[10]通过基于类间距离和互信息的特征选择方法获得最优时频域特征，输入到 BP 神经网络进行识别。

现有方法对钢丝绳漏磁信号损伤检测的方式大致可分为两类：一类是通过对原始信号进行降噪、消除股波噪声等得到较为纯净的信号，然后通过观察处理后信号的异常冲击来判断损伤；另一类是通过对处理后的信号进行相关特征量的提取，借助神经网络进行分类。前者方法过于依赖先验知识，预处理的方法会对最终判别结果产生较大的影响，而后者又需要大量的数据对模型进行训练，模型的准确率和泛化性能不够稳定。

峭度可以衡量一组数据的离散程度，常用于检测冲击信号，现已被应用到轴承故障诊断、转子故障诊断、齿轮箱故障诊断等领域。但是，峭度在钢丝绳损伤检测中的应用却还近乎空白。钢丝绳通常由铁磁性材料制成，具有非常高的磁导率。励磁后的钢丝绳如果没有出现缺陷，磁力线就会被紧密约束在钢丝绳中。如果钢丝绳存在缺陷，那么缺陷处的磁导率就会发生改变，导致磁力线被折射到缺陷表面周围的空气中，反映在磁性传感器所输出的漏磁信号中就是一个较大的冲击。因此，峭度同样可以应用到钢丝绳漏磁信号的损伤检测中。

本文首先对峭度进行了介绍，利用峭度对偏离分布范围规律之外异常信号值的敏感性，结合分段、平移的思想原理提出了短时峭度法；其次，定义了短时峭度指标，用于寻找计算短时峭度的最优参数，然后对试验台所采集到的漏磁信号进行分析，验证了方法的可行性；最后，以实际工况中所采集到的漏磁信号为例，与传统超门限决策方法进行了对比，验证了短时峭度法在钢丝绳漏磁信号损伤检测中的优越性。

1 峭度与短时峭度

1.1 峭度

对于由N个点组成的信号，其4 阶中心矩µ4可以与标准差的 4 次方相除，用于估计概率密度曲线的平坦度，一般称为峭度µ4′，其表达式为

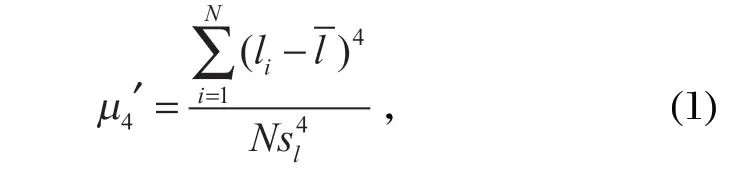
式中：li为第i个点所对应的值；为信号的均值；sl为信号的标准差。

峭度反映了信号在主体分布中趋近于 0 的相对比例，可用于验证所分析的信号是否服从高斯分布。一般情况下，当服从高斯分布时，理论上峭度值等于3，而当信号中含有高峰值成分时，理论上峭度值会大于 3。

1.2 短时峭度

对于一个含有较大冲击的信号而言，如果对其进行峭度的求取，最后只能得到一个峭度值。虽然一定程度上在钢丝绳的漏磁信号检测中可以反映钢丝绳的健康状态，但是无法对损伤位置进行准确的定位，也无法应用到工程实际中。为了解决这个问题，笔者利用分段、平移的思想，提出了短时峭度法。该方法在对信号进行峭度值计算时，只需要取信号中部分连续的点，而不是所有的点。每一次计算后，整个窗就会按照一定的步长进行移动，如图 1 所示。每个峭度值的位置对应着每个窗内中间点所在的位置。当所有的峭度值都确定后，可以据此画出一条基于位置的曲线，定义为短时峭度曲线。在接近数据尾端时，可能由于窗宽过大，导致出现数据点不够的情况。解决该问题有几种不同的处理方法，如补点，即从数据首段开始取相应个数的点补充到窗内进行计算。但是，为了避免数据首段本身就存在损伤信号，导致计算出来的峭度值出现异常，采用自适应缩小窗宽的方式。该方法即在接近计算数据尾端的峭度值时，让窗宽自动调整到适当的大小来进行峭度值的计算。在计算每个峭度值时，可以利用前值的计算结果，因此可以提高整个短时峭度的计算速度。

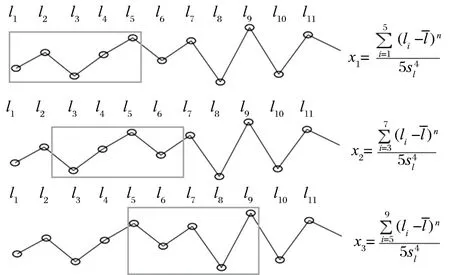
图1 短时峭度的计算过程 (M=5,S=2)Fig.1 Calculation process of short-time kurtosis(M=5,S=2)

1.3 短时峭度

在计算短时峭度时，会涉及到窗宽和步长 2 个参数变量，而这 2 个参数的变化会直接影响到短时峭度图最终呈现的效果。为了使短时峭图能够直观地反映出钢丝绳的损伤状态和准确的损伤位置，定义了短时峭度作为适应度函数，以便于在给定范围内寻找到最优的窗宽和步长。短时峭度指标

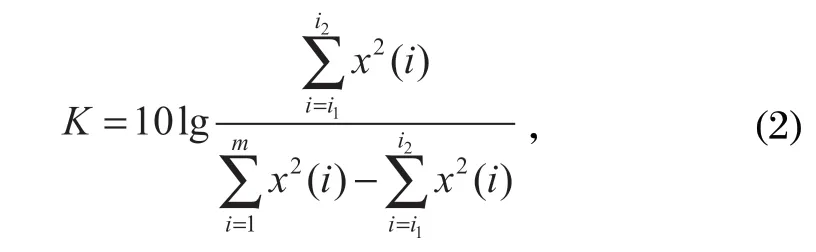
式中：x(i) 为处理后的短时峭度图中第i个点的峭度值；i1为峰值峭度的起始点；i2为峰值峭度的终止点；m为短时峭度曲线中的最后一个点。

K越大，表示峰值峭度所包含的能量相较于整体的能量 (除去峰值峭度自身包含的能量) 越大，即峰值峭度周边的峭度指标信号更加平滑，突变较小。

1.4 损伤位置计算

在进行短时峭度图绘制时，若峭度值发生很大变化，就表示可能存在机械冲击或信号有问题。该理论同样适用于钢丝绳的漏磁损伤检测。

通过短时峭度曲线，可以观察到峭度值的变化趋势。当钢丝绳出现损伤缺陷时，其损伤处的漏磁信号转换为峭度值后会出现很大的变化，反映在短时峭度曲线上体现为较大的峰值。根据峰值所对应的横坐标，可反推出损伤位置，便于后续钢丝绳的维护和处理。损伤位置的计算公式为

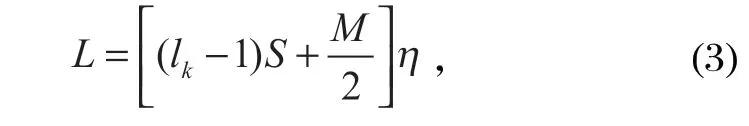
式中：L为损伤位置距离启测点的距离；lk为短时峭度图中该峰值所对应的短时峭度曲线的点数；S为步长；M为窗宽；η为探伤仪编码器的采样间隔距离。

2 基于短时峭度法的钢丝绳损伤检测

为了能够提高钢丝绳损伤检测的准确率及损伤位置的定位精度，提出了一种基于短时峭度法的钢丝绳损伤检测及定位算法框架。钢丝绳损伤检测及定位流程如图 2 所示。该流程主要包括：漏磁信号预处理，参数初始化及最优参量选取，损伤判别及损伤定位。具体步骤如下。

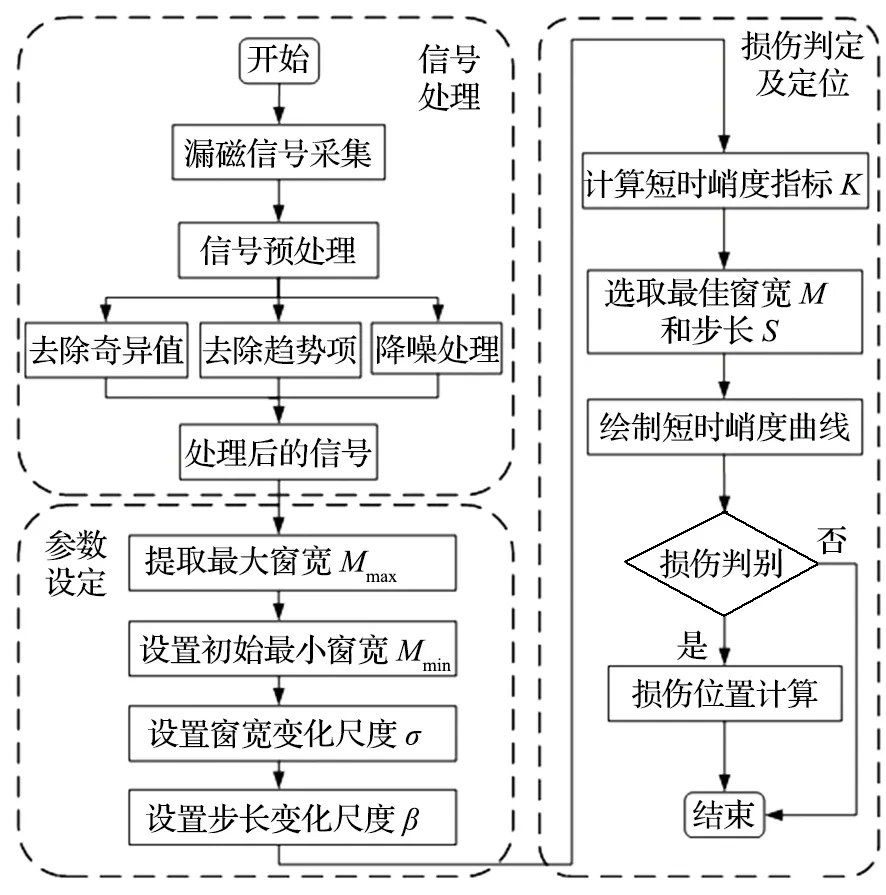
图2 钢丝绳损伤检测及定位流程Fig.2 Process flow of damage detection and location for steel wire rope

(1) 利用霍尔型探伤仪采集钢丝绳的漏磁信号，并依次对信号进行奇异值的剔除、趋势项的去除以及噪声的消除。

(2) 通过处理后的信号提取最大窗宽值，并分别设置窗宽和步长的变化尺度。而后，遍历计算短时峭度指标，通过对指标进行筛选，得到对应的最优窗宽和最优步长。

(3) 通过最优窗宽和步长绘制短时峭度曲线图，并对钢丝绳的健康状态进行判别。最后对判定为损伤的部位进行定位计算。

3 试验分析

现实环境中的局部不规则信号，无论是由于冲击造成的，还是由于测量故障产生的，峭度对于偏离分布规律之外的异常信号值都是非常敏感的。因此，可以在理论上讲，只要分析一下峭度值的变化情况，就可以比较容易地发现这种异常的信号。

为了验证所提出方法的可行性，笔者借助钢丝绳的磁核模型[11]构建了一个由 50 000 个点构成的仿真信号，并借此进行测试。钢丝绳损伤漏磁仿真信号及短时峭度如图 3 所示。由图 3 可以观察到，仿真信号的短时峭度图中有一个十分明显的高峰，波峰对应的峭度值已经达到了 8.7。

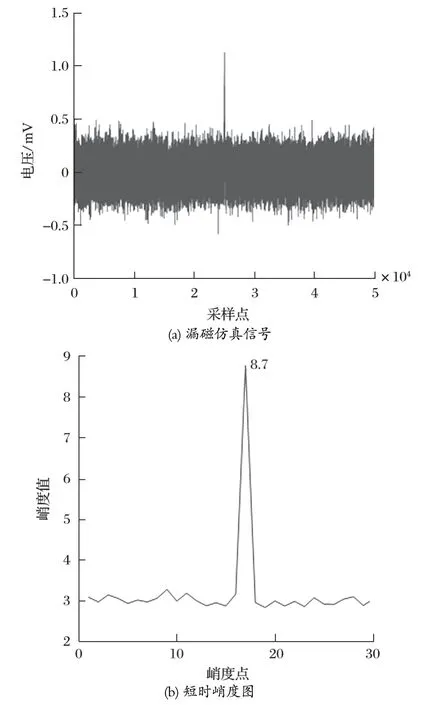
图3 钢丝绳损伤漏磁仿真信号及短时峭度图Fig.3 Simulation signal and short-time kurtosis map of damage MFL of steel wire rope

为探究窗宽M、步长S以及短时峭度指标K之间的关系，对100、200、…、5 000 个数据点的规律进行变化，最终得到关于窗宽、步长和短时峭度指标之间的关系，如图 4 所示。

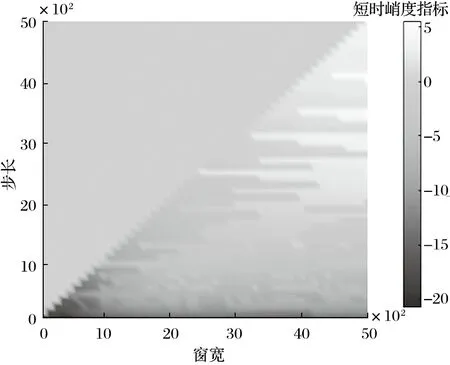
图4 仿真信号 M、S、K 关系图Fig.4 Relationship among M,S and K of simulation signal

由图 4 可观察到有一片 0 值区域，这是由于步长的值不可以超过窗宽值所造成的现象。但是，该现象对于窗宽和步长的最优值选取并没有实质性的影响。而K之所以出现负值，是因为在计算K值时，峰值信号的能量远小于除了其本身之外的信号能量之和，所以造成了K为负值。与此同时，也可以观察到窗宽M和步长S对K的影响并非是线性关系。在关系图中存在多处优质的取值范围带，在该范围内取值所绘制的短时峭度图基本上是符合要求的。在关系图中存在一个最大的K值，此时窗宽和步长分别对应 5 000个数据点，以此参数绘制的短时峭度图效果也是最好的。该能量带的存在证实了在计算K时，总会可以求得一个范围内最优的窗宽与步长，使K值最大，且对应的短时峭度图能较好地反映损伤特征。

对任意钢丝绳的损伤漏磁信号而言，在不同窗宽与步长的情况下，计算其所对应的短时峭度指标K并进行比较。当K值最大时，所对应窗宽和步长的值为最优值。

为了验证所提方法的有效性，搭建了钢丝绳损伤检测试验台。该试验台主体由支撑平台、锁紧装置和钢丝绳样绳 3 部分构成，如图 5 所示。试验选用6×37S-FC 型号的钢丝绳，探伤仪则选用 Y66 型便携式探伤仪。

图5 钢丝绳损伤检测试验台Fig.5 Damage detection test bench for steel wire rope

首先，在钢丝绳样绳上人为加工损伤。然后，采用 Y66 霍尔型钢丝绳探伤仪对钢丝绳进行探伤检测。推动探伤仪在钢丝绳样绳上移动，利用探伤仪采集装置采集试验信号并在电脑中显示。将试验数据保存为txt 文本格式，便于后续试验数据的调用和分析。

采集到的部分信号如图 6(a) 所示。该部分损伤信号包含 4 000 个点，且信号被噪声信号干扰严重，钢丝绳损伤判断受到很大的限制。随后对采集到的信号进行了降噪处理，处理后的信号如图 6(b) 所示。

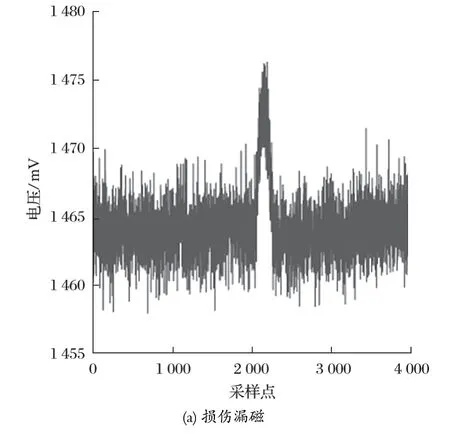
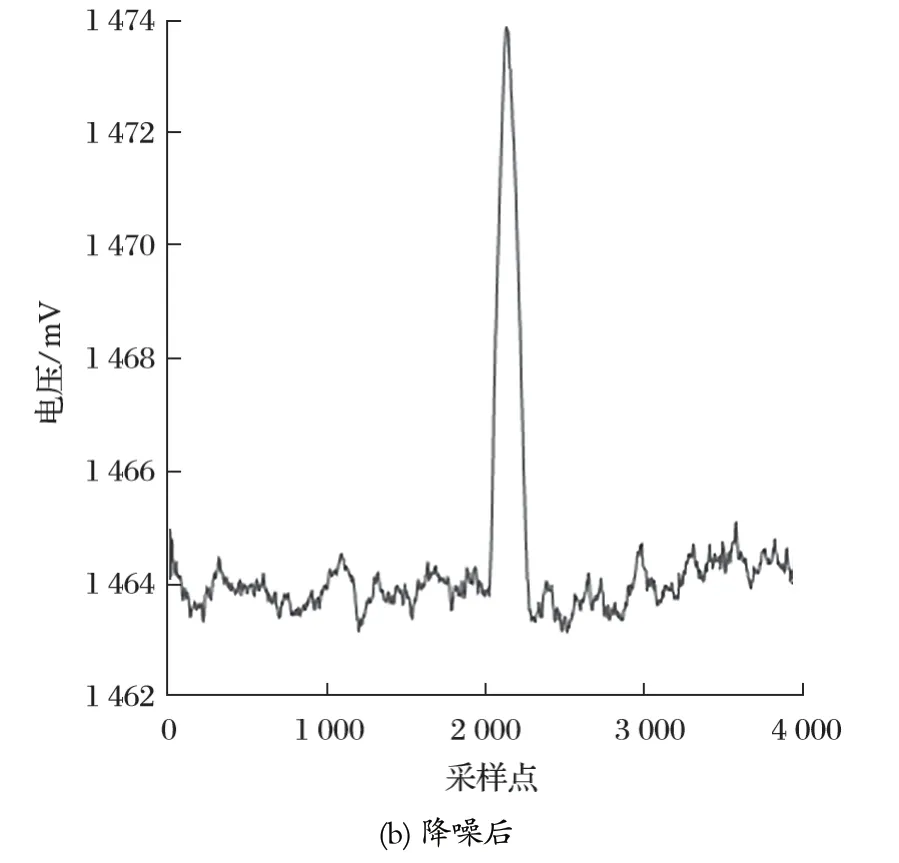
图6 钢丝绳损伤漏磁及降噪后的试验信号Fig.6 Damage MFL of steel wire rope and test signal after noise reduction

为了能够找到较好的窗宽和步长来绘制短时峭度图，规定窗宽和步长由 10、20、…、400 个数据点的规律进行变化。最终得到关于窗宽、步长和短时峭度指标之间的关系图，如图 7(a) 所示。在图 7(a) 可以观察到，当窗宽范围在 300～400 个数据点之间，步长在 150～350 个数据点之间时，存在多条高亮的能量带。在这些能量带中存在一个最大K值，对应的窗宽和步长分别为 360 和 340 个数据点。以该参数作为最终短时峭度图的绘制参数，得到如图 7(b) 所示的短时峭度图。通过图 7(b) 可以观察到，峰值时刻的峭度值介于 13～14 之间，远高于正常峭度值范围。

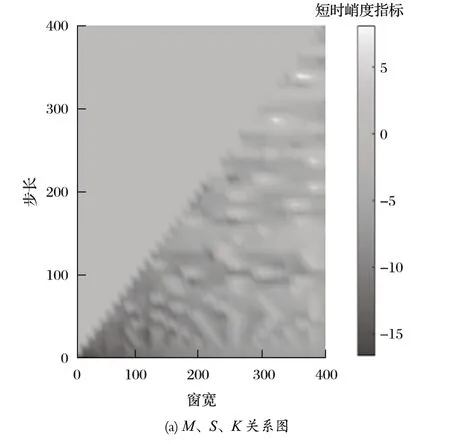
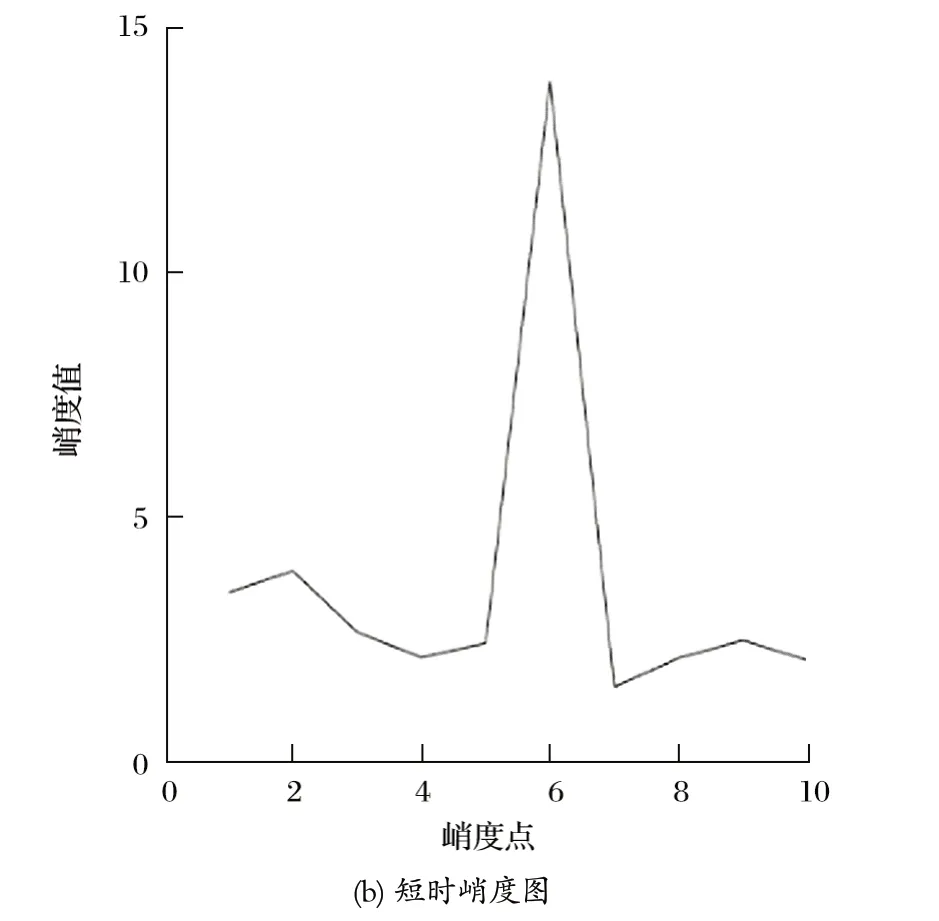
图7 M、S、K 取最优值时的短时峭度图Fig.7 Short-time kurtosis map at time of optimal value of M,S,K

为了验证所提出的方法对损伤位置判定的准确性，同时凸显本文方法的优越性，笔者选取了一段在某煤矿企业采集的含有 3 处损伤的真实信号，并与基于小波变换的阈值判别法进行对比。如图 8(a) 所示为原始信号，由于工况比较恶劣其中含有大量的噪声；图 8(b) 为预处理后的漏磁信号。

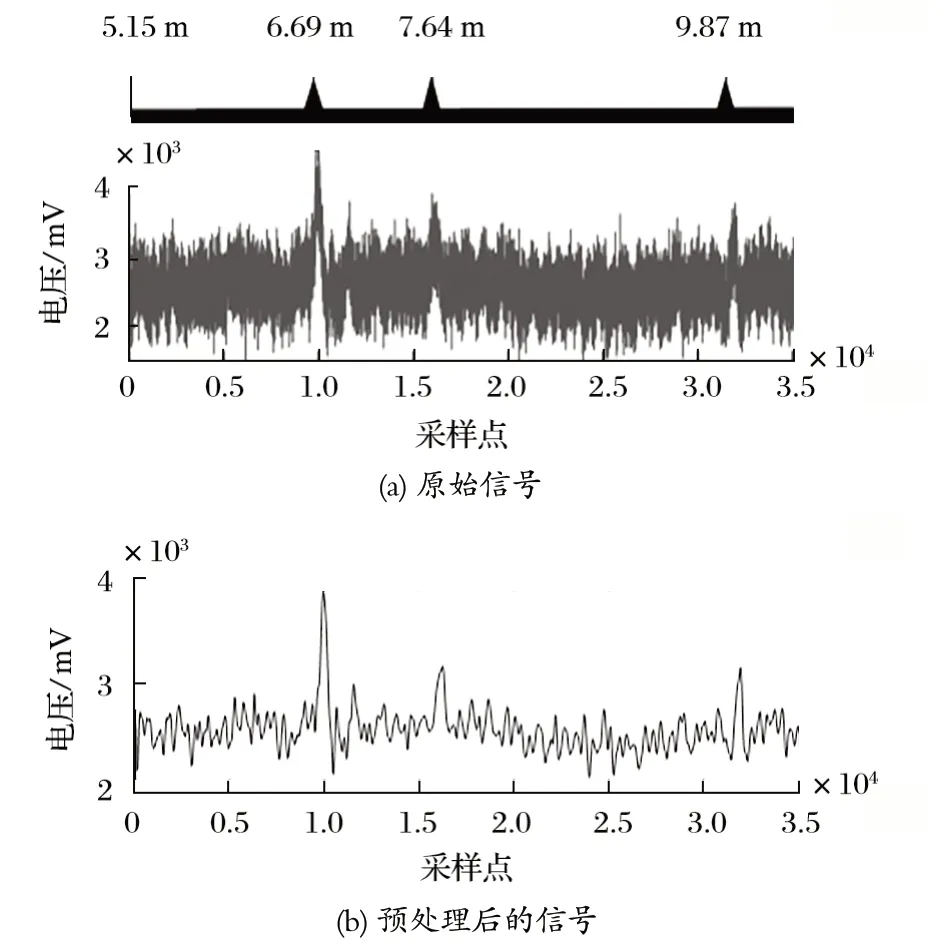
图8 实际工况所采集的的信号Fig.8 Signal collected in actual working mode

利用传统超门限决策方法对预处理后的信号进行阈值设定，不同信号所设定的阈值也不尽相同，对使用者自身经验的要求较高。因此，模拟设定了 2 个阈值，分别为 3 170 和 3 100 mv。基于小波变换的阈值判别法如图 9(a) 所示。通过图 9(a) 可以观察到当阈值为 3 100 mv 时 3 个钢丝绳的损伤可以被识别出来，而当阈值为 3 170 mv 时，第3 个损伤正好被卡在阈值之外被归为了无损伤。因此可以看出，通过人为阈值设置的方式对钢丝绳损伤进行判别，由于主观性较大，过分依赖先验知识，所以最终检测出来的结果准确性不稳定。基于短时峭度法的损伤判别法如图 9(b) 所示。由图 9(b) 可以观察到短时峭度曲线一共有 4 个峰值，除去 3 附近的峰值，其余峰值均在 4 以上，说明该段信号中包含了 3 处钢丝绳损伤。

图9 2 种方法的分析结果对比Fig.9 Comparison of two methods in analysis results

除了对比损伤判别的准确性，笔者还对损伤位置进行了计算，如表 1 所列。由表 1 可以看出，计算的损伤位置与实际的损伤位置十分相近，平均误差率为0.86%。

综合图 9 和表 1 可以看出，采用短时峭度法对钢丝绳进行损伤检测的效果相较于基于小波变换的阈值判别法的检测效果要更加稳定，其不需要依靠先验知识设定阈值，降低了对检测者自身的要求，使损伤检测更加方便；通过短时峭度法所得到的损伤位置和真实损伤位置相差极小，可帮助检测者更加简单高效地在钢丝绳上寻找到损伤位置。

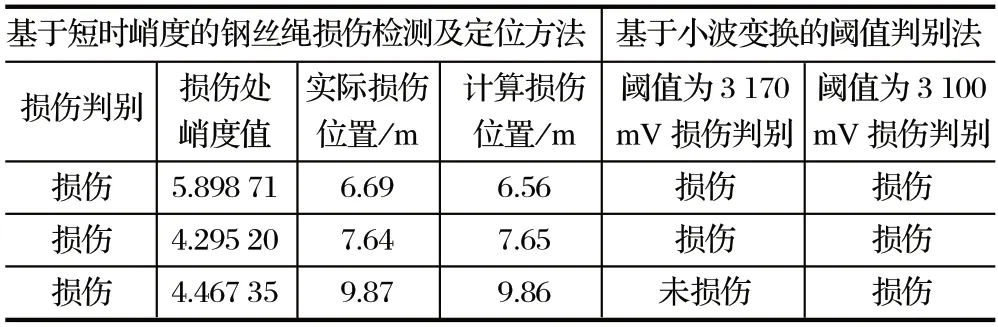
表1 实际损伤与计算损伤位置Tab.1 Actual damage location and calculated damage location

4 结论

针对钢丝绳漏磁信号损伤检测问题，提出了一种短时峭度方法，并将该方法应用于钢丝绳漏磁信号的损伤检测及损伤定位中。数据分析结果表明：

(1) 峭度对于偏离分布规律之外的异常信号值的敏感性，是可以有效应用在钢丝绳漏磁信号的分析中，对钢丝绳损伤特征进行有效提取；

(2) 将峭度指标与分段、平移的思想进行有机结合，增大了模型整体的泛化性能，避免了单一峭度指标适用范围窄、可解释性差等问题；

(3) 所提出的短时峭度指标，实现了在规定范围内对最优窗函数与步长的寻找，减小了最优参数寻找的难度，较大提高了寻优的效率；

(4) 通过短时峭度图，根据每个峰所对应的峰值可以客观判断钢丝绳的损伤情况，不需要检测者依赖自身的先验知识进行门限值的设定，较大幅度地提高了检测的效率；

(5) 相较于传统借助神经网络进行特征提取的处理方法，该方法不涉及多种指标的计算以及大量数据的训练，使用上的限制更少，且能够对损伤位置进行准确地定位。