一类不确定变速风力涡轮机系统的实际跟踪控制

徐文青,李 健,吴昭景

(烟台大学数学与信息科学学院,山东烟台 264005)

1 引言

风力发电由于其环保、高效和可持续性等优点目前已成为主要发电方式之一.变速风力涡轮机是风力发电的核心设备.为了提高风能转化效率,需要根据风力变化有针对性地调整涡轮机转子转速[1–3].因此,涡轮机转子转速调节问题一直是风力发电领域的核心控制问题.需指出的是,由于涡轮机系统非线性特性以及参数、扰动等不确定性的存在,该领域内许多具有显著科学意义和实际应用价值的控制问题尚未解决.

为了最大限度地捕获风能,涡轮机系统需要根据风力变化在线调节转子转速以达到期望转速(即参考信号).近20年以来,变速风力涡轮机系统的转子转速调节问题得到持续研究[3–20].然而在实际工程中,受测量设备的不准确性和外部工作环境等因素的影响,描述系统动态的模型不可避免地存在不确定性(例如系统未知参数和外部扰动),这往往给控制设计和分析带来本质困难.针对不确定变速风力涡轮机系统转子转速调节问题,多种控制设计方法被提出,例如:鲁棒控制[4]、自适应(非鲁棒)控制[3,5–6]、滑模控制[7–9]等,但现有文献对系统不确定性和参考信号(即期望转速)都有较严格的约束,限制了理论结果的可应用性.具体地:

1) 现有文献要求系统参数部分或全部已知,扰动可导或其上界已知.具体地,文献[4]要求系统部分参数未知而其他参数精确已知,文献[3]允许系统参数未知但未考虑外部扰动,文献[5,8–9]虽然同时考虑系统存在未知参数和扰动,但扰动必须上界已知或扰动本身及其一、二阶导数必须有界.需要指出的是,由于变速风力涡轮机结构的复杂性,许多系统参数的真实值往往难以获得.此外,恶劣的工作环境常导致涡轮机不可避免地遭受外部扰动的影响,且扰动往往具有非光滑特性(甚至不连续性)和较严重的未知性(例如上界未知).上述不确定性的存在将导致涡轮机系统转子转速调节控制设计中出现本质的技术困难.

2) 现有文献要求参考信号具有较强的光滑性(例如至少二阶可导)和可测性(例如其一或二阶导数可测).具体地,文献[3,5–6]要求参考信号二阶可导,因此排除了一大类低光滑性(例如仅一阶可导)信号.文献[3,5,7,10,12]除了要求参考信号本身可测,还要求其一或二阶导数可测,这意味着需要更多的测量设备来获取更多的信号,加重了控制器的测量负担.因此,当参考信号具有较强的一般性(仅一阶可导)且仅有少量信息可量测(例如其导数不可测)时,现有的控制设计方法无效.

注意到现有文献对系统不确定性和参考信号两方面的限制,未来一个值得进一步研究的有意义的问题是: 当系统存在较强的不确定性以及参考信号仅有少量信息可测时,如何设计控制器使系统转速跟踪到期望的转速?这亦是本文的主要控制目标.与相关文献不同,本文所研究的变速风力涡轮机系统参数全部未知,系统的两个通道(转子动力学通道和励磁机动力学通道)都含有扰动且扰动不必可导,上界不必已知,因而具有更严重的不确定性,现有控制设计方法不能适用.为了解决上述问题,本文首先定义坐标变换,给出误差系统,将原系统的跟踪控制问题转化为误差系统的镇定控制问题.然后,对误差系统选择适当的李雅普诺夫函数,将自适应动态补偿技术融入反推控制设计框架,给出自适应状态反馈控制器显示形式.通过巧妙地选择自适应律,有效克服现有文献对系统不确定性及参考信号的严格限制,同时使得所设计的控制器保证闭环系统所有信号有界且系统输出(即转子转速)在某个时刻之后到达并且保持在参考信号(即期望转速)的给定邻域内.最后,仿真实验验证理论结果的有效性.值得指出的是,本文所设计的控制器仅依赖于参考信号本身而不依赖其导数,因而降低了相关文献对参考信号可量测性的限制.

本文的其余部分组织为:第2节给出所研究的变速风力涡轮机系统和控制目标;第3节展示控制设计的过程;第4节分析闭环系统的性能;第5节通过仿真实验验证理论结果的有效性;第6节是总结.

2 问题描述

本文考虑如下一类变速风力涡轮机系统[2–3],其结构如图1所示.

其中:ω(t)∈R和If(t)∈R分别是转子转速和场电流,uf(t)∈R是控制输入,d1(t),d2(t)∈R是扰动(包含了系统未建模动态和外部环境对系统的影响),pi,i=1,2,···,5是未知的系统参数,它们定义如下:

其中:J=Jm+γ2Je是总转动惯量,Jm,Je∈R分别为涡轮端的转动惯量和发电机端的转动惯量,γ=∈R是齿轮传动比,B ∈R是总摩擦系数,c,Kϕ ∈R是风力涡轮机操作或设计相关的常数,kω是恒定风速到功率传递参数,Rf∈R是转子磁场的电阻,L是电路的恒电感值.系统(1)的两个方程分别描述了转子动态和励磁机动态,其结构分别由图1和图2所示.

图1 变速风力涡轮机系统结构图Fig.1 Structure graphing of the overall system of VSWT

图2 变速风力涡轮机电气子系统结构图Fig.2 Structure graphing of the electrical subsystem of VSWT

本文的控制目标是对变速风力涡轮机系统(1)设计控制电压uf使所得闭环系统的所有信号有界,同时系统输出(即转轴转速ω)实际跟踪到给定参考信号(即期望转速ωr,满足如下假设1),即,对给定的跟踪精度λ1(任意正常数),存在某个有限时刻T >0,使得|ω −ωr|<λ1,∀t>T.

为确保控制目标的实现,如下给出扰动和参考信号需满足的条件.

假设1存在未知常数M1,使得

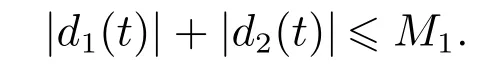
假设2存在未知常数M2,使得

系统(1)中d1,d2分别表示未建模动态(例如,d1可表示扭转效应)和外部环境对系统的影响(例如,d2可表示电子元器件发热导致的能量损耗).假设1表明扰动仅需有未知上界且不必是光滑的,而现有文献或要求扰动具有已知上界(见文献[8–9])或扰动必须是光滑的(见文献[5]),因此本文所研究的系统具有更严重的不确定性且允许非光滑(甚至非连续)扰动.假设2表明参考信号(即期望转速)仅需一阶可导,而在文献[3,5–6]中要求参考信号二阶可导,因此本文所提理论结果将适用于更广泛类型的参考信号.

3 控制设计

对系统(1)引入下面的坐标变换1为了减少符号负担,在不引起混淆的情况下,下文将忽略自变量t.:

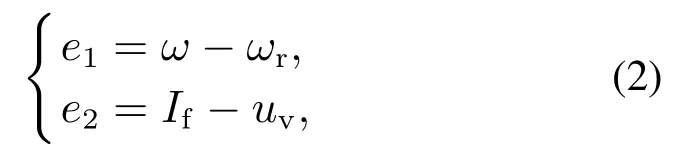
其中uv是待定的虚拟控制.由式(1)–(2)可以得到以下误差系统:

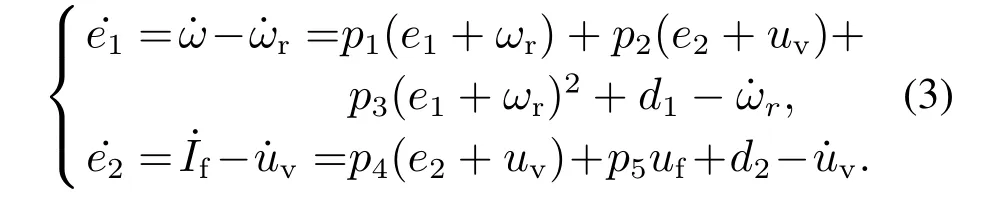
如下通过两步反推变换设计控制器:

步骤1定义Lyapunov函数

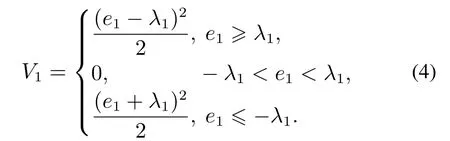
根据复合函数连续可微性的判据,容易验证V1关于时间变量t是连续可微的,且V1关于e1的导数为

由式(3)的第1个方程,式(4)–(5)得到

其中:ϑ(k1)是C1类函数且满足Nussbaum增益性质2函数ϑ ∈C1满足(例如cosk1),k1满足如下自适应律:

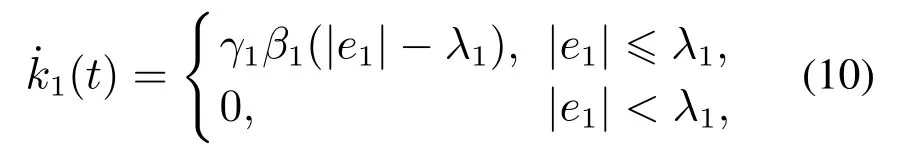
注1与已有文献不同的是,本文所选取的虚拟控制uv不含有(见式(9)),因此后续推导过程中求虚拟控制的导数时不需要对求偏导(见下文式(15)),从而不需要参考信号关于时间变量的更高阶导数.这种处理技术去除了已有文献对ωr具有更高阶导数的限制.

接下来分两种情形讨论.

其中λ2是任意给定的正常数.容易验证V2关于时间变量t是连续可微的,且V2关于e2的导数为

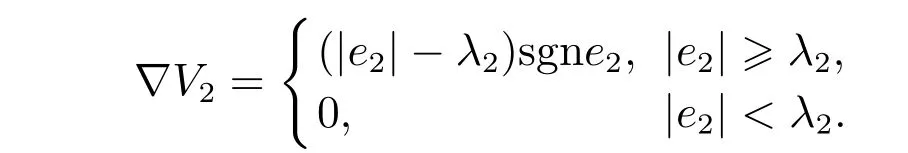
根据式(3)的第2个方程和式(9)可得

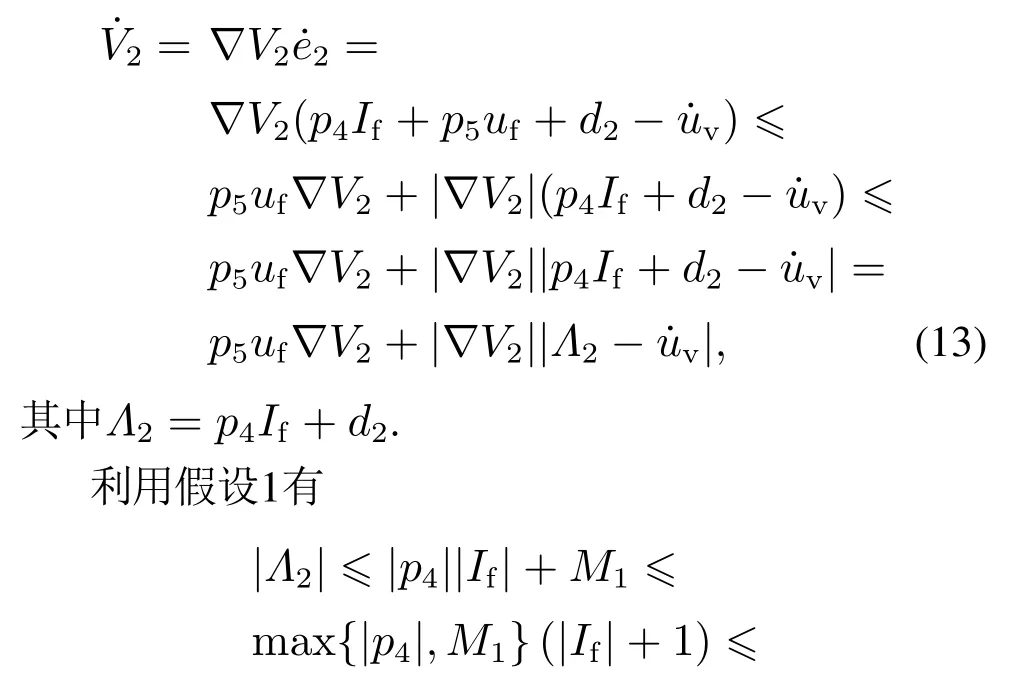
接下来分两种情形讨论.

注2由式(7)(16)可以看出,未知参数以及扰动和参考信号的未知界被集总到和中,随后通过巧妙地选取自适应律˙k1和˙k2来补偿系统存在的不确定性和未知性.

注3如下将利用式(11)(20)首先给出k1(t),k2(t)的有界性(由下文命题1给出),然后证明闭环系统的期望性能(由下文定理1给出).

4 性能分析

本节分析所得闭环系统的性能.作为准备,首先给出控制增益k1,k2的有界性,然后给出主要定理总结本文的主要结果.

命题1分别由式(10)和式(19)定义的控制增益k1(t),k2(t)在[0,+∞)上是有界的.

证首先证明k2(t)在[0,+∞)上是有界的.由(t)≥0得到k2(t)是单调递增函数.对式(20)两边在[0,t]上积分有

亦形成矛盾.所以假设不成立,则k1(t)在[0,+∞)上是有界的.同理可得V1(t),e1(t)在[0,+∞)上有界. 证毕.

定理1对于满足假设1和假设2的系统(1),自适应控制器(10)(18)–(19)保证所得闭环系统具有以下性能:

1) 闭环系统的所有信号在[0,+∞)上有界;

2) 对于任意的常数λ1>0,存在一个有限时刻T >0,使得|e1|=|ω −ωr|<λ1,∀t>T.

证先证闭环系统信号的有界性.实际上,由定理1及方程组(2)的第1个方程可得ω在[0,+∞)上有界,进而式(9)可给出uv在[0,+∞)上有界,方程组(2)的第2个方程可给出If在[0,+∞)上有界,最后式(18)给出uf在[0,+∞)上有界.

5 仿真

本节首先给出本文所设计控制器的仿真结果,验证所提方法的有效性.然后将本文所设计控制器仿真结果与PID控制器仿真结果作对比,体现本文所提方法的先进性.

5.1 仿真实验

本小节通过仿真实验验证所设计的控制器的有效性.对系统(1),系统参数的真实值由表1[2]给出,参考信号为

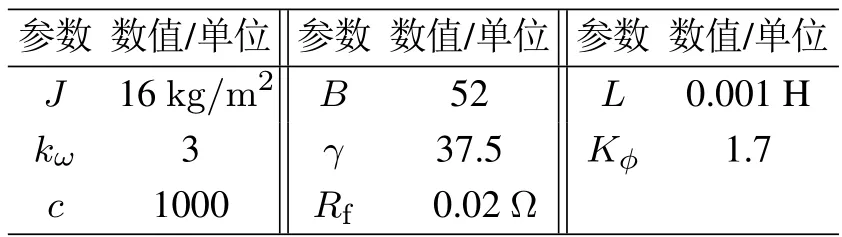
表1 变速风力涡轮机模型参数Table 1 Values of the parameters for VSWT

应用控制器式(18)(其中ϑ(ki)=coski,i=1,2),分别在以下两种情形下进行仿真.

1) 假设扰动、跟踪精度、控制器参数和初值条件为

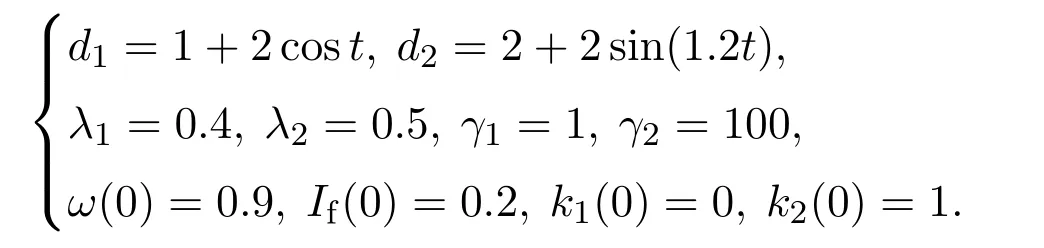
2) 假设扰动、跟踪精度、控制器参数和初值条件为

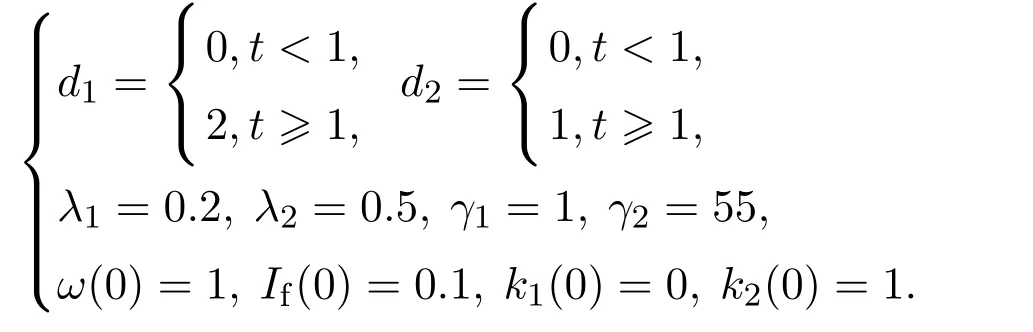
在MATLAB中仿真,得到仿真图3–7.其中,图3表明跟踪误差在某时刻之后进入并保持在原点的给定邻域.图4表明系统输出ω在某时刻之后跟踪到并保持在参考轨迹的给定邻域.图5–6分别表明闭环系统的状态和控制电压是有界的.图7表明时变控制器增益k1和k2是有界的.

图3 转速跟踪误差(左图情形1,右图情形2)Fig.3 The rotor speed tracking errors(left for case 1,right for case 2)

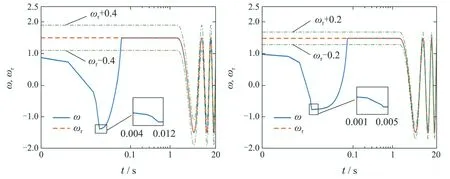
图4 转速跟踪效果(左图情形1,右图情形2)Fig.4 The rotor speed tracking results(left for case 1,right for case 2)

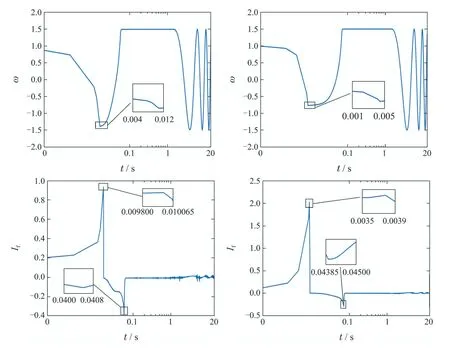
图5 状态轨迹(左图情形1,右图情形2)Fig.5 Trajectories for the states(left for case 1,right for case 2)

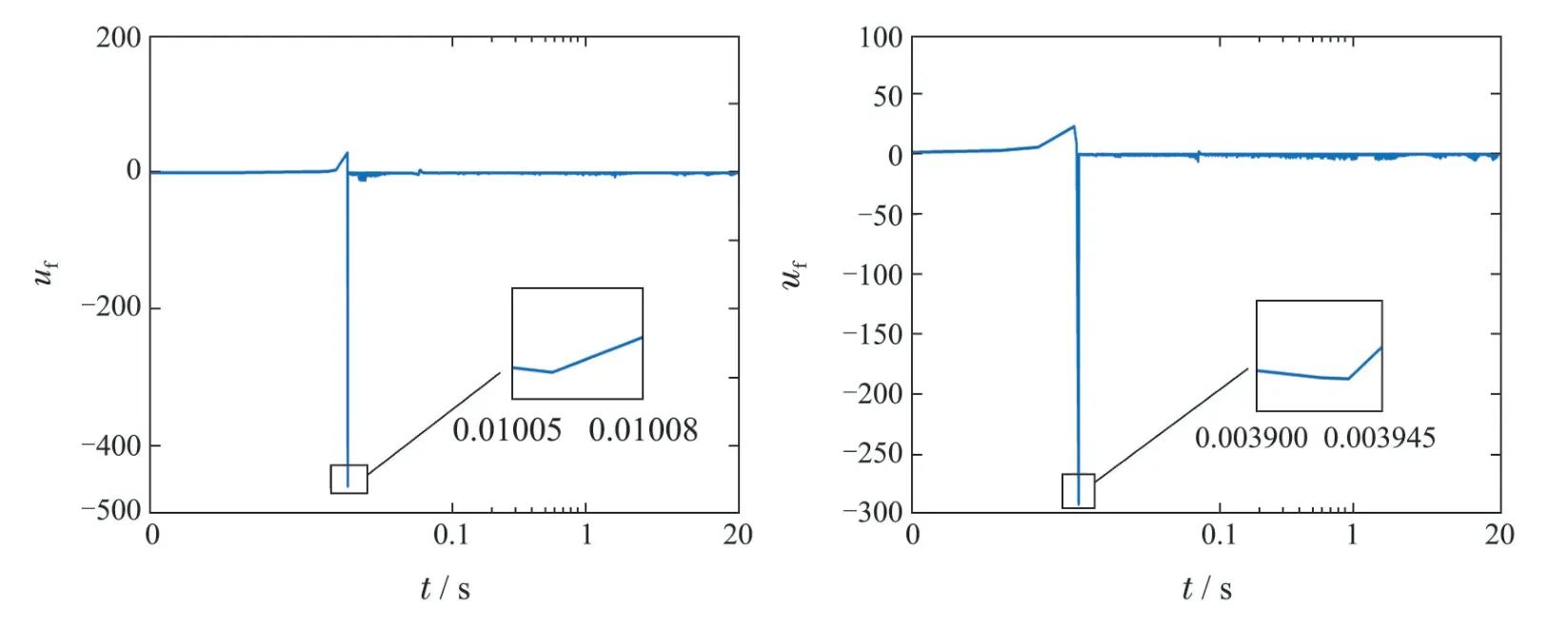
图6 控制轨迹(左图情形1,右图情形2)Fig.6 Trajectories for the control law(left for case 1,right for case 2)

图7 控制器增益k1和k2 的轨迹(左图情形1,右图情形2)Fig.7 Trajectories for the time-varying controller gains k1and k2 (left for case 1,right for case 2)

5.2 与PID控制的比较

本小节给出所提控制器与PID控制器的仿真结果比较,以体现本文所提控制器在控制器参数选取方面的灵活性.

实际上,本文的控制目标也可由PID控制器实现.然而,与本文控制器参数可以较方便地选取(即仅需γ1,γ2为正)不同的是,PID方法的控制效果严重地依赖其控制器参数的选取,随便选取的控制器参数难以保证期望的控制性能.例如,对系统(1)选取如下PID控制器:

其中:cp,ci,cd是控制器参数,e1,分别由式(2)–(3)的第1个方程给出.在第5.1节所选取的系统参数、参考信号以及情形1下,选取PID控制器参数为cp=17.2,ci=−3,cd=0.025,在情形2下,选取PID控制器参数为cp=9,ci=−1.5,cd=0.3,所得仿真图8显示跟踪误差不能在某时刻之后保持在原点的给定邻域中.

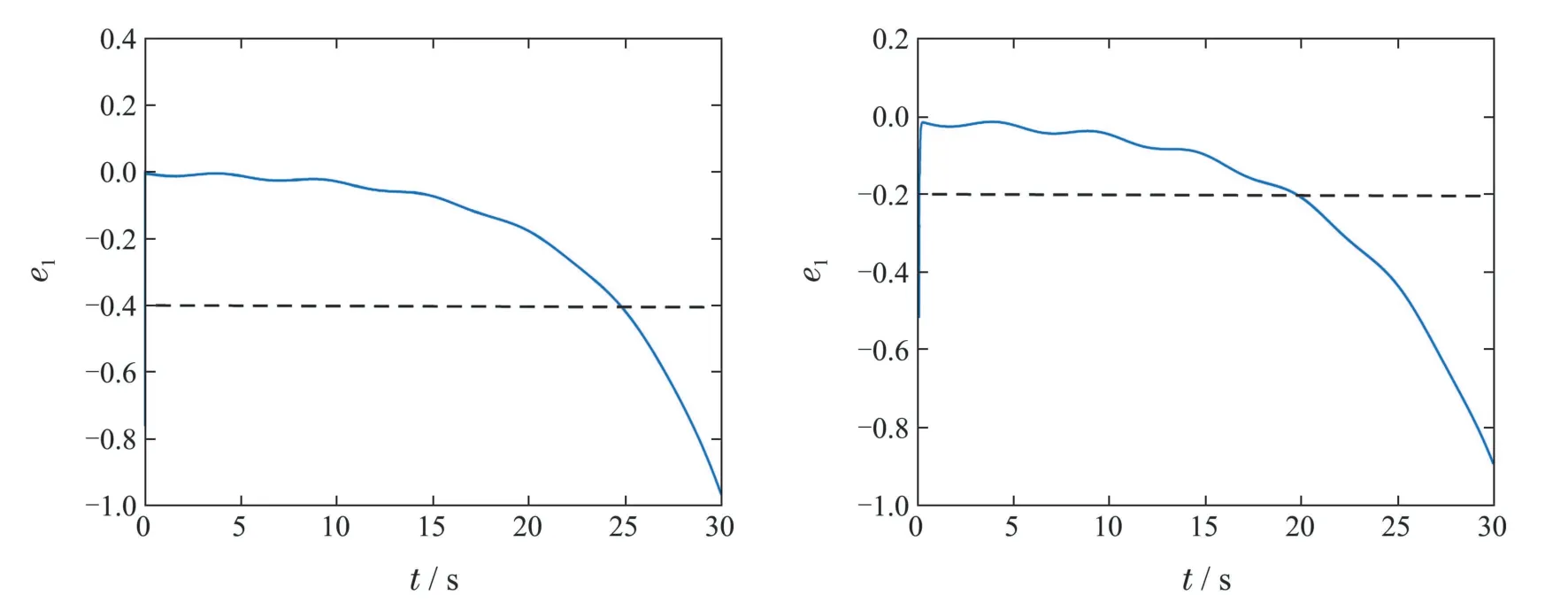
图8 PID 跟踪误差轨迹(左图情形1,右图情形2)Fig.8 Trajectories for the tracking errors by PID method(left for case 1,right for case 2)

6 总结评述

本文解决了一类变速风力涡轮机系统的跟踪控制问题.由于所研究的系统参数全部未知、两个通道都含有扰动且扰动不必可导,上界不必已知,因此现有的控制设计方法无效.为此,本文将自适应动态补偿机制与反推方法结合,给出了系统实际跟踪控制设计与分析的新框架.在此基础上,给出了状态反馈控制器的显式形式,保证闭环系统所有信号有界且涡轮机转子转速实际跟踪到期望的转速.此外,由于所设计的控制器仅依赖于参考信号本身而不依赖其导数,因而降低了相关文献对参考信号可量测性的限制.需指出的是,本文仅关注闭环系统信号的有界性等稳态性能而忽视跟踪到达时间和超调等实际控制过程中经常关注的瞬态性能.因此,如何设计反馈控制器使得在保证闭环系统稳态性能的同时还确保预先设定的暂态性能是非常有意义且值得进一步研究的控制问题.