一类含不匹配干扰的非线性系统非递归鲁棒/自适应一体化控制律设计

董 鑫,张传林

(上海电力大学自动化工程学院,上海 200090)

1 引言

本文主要研究具有如下形式的一类含不匹配干扰的非线性系统的跟踪问题:

1Ni→j={i,i+1,···,j},∀i,j ∈N,i≤j.

针对不确定系统(1),现有文献中已有诸多控制策略用来求解系统的干扰抑制与跟踪控制问题.比较常见的方案是通过选取较大的控制增益来抑制干扰的不良影响,如非线性H∞控制[1]、齐次压制控制[2]、几乎干扰解耦方法(almost disturbance decoupling)[3]等.但是这类方法在理论上无法实现系统输出的精确跟踪,且需要消耗较大的控制能量.

当系统(1)中的干扰di存在于外源系统时,非线性输出调节控制策略常用来解决此情况下系统的精确跟踪控制问题,见文献[4–7]等.而当干扰外源模型完全未知或误差较大时,这类方法无法重构干扰模型以及获取干扰的不稳定信息结构,因此难以设计出有效的输出调节律[8].另一方面,在干扰满足一定的有界性假设条件时,基于干扰观测技术的复合控制策略可以有效地补偿干扰对系统性能的影响,从而提升控制精度.这类方法已经得到了学术界的广泛关注,例如,文献[9]提出了一系列基于主动抗干扰技术的控制策略,可用于解决系统(1)的精确跟踪问题.针对一个具有稳定零动态、可反馈线性化的非线性系统,文献[10]提出了一个扩张高增益观测器,通过选取合适的观测器增益,能够实现标称模型的性能恢复.基于误差放大策略和双极限齐次估计理论,文献[11]给出了一个固定时间收敛的干扰观测器.上述仅举几例,衍生出的理论及工程应用文章可见于文献[12–15]等.

从反馈控制设计的角度来说,结合上述的干扰软测量及前馈补偿策略,基于反步法(或扩展反步法等)的递归控制设计策略是解决系统(1)的跟踪控制问题较为常见的方法,如文献[16–19]等.但是以此类递归方法来解决受扰系统的控制问题有一些明显的弊端,主要可归结于如下两点:1)递归控制过程中产生的虚拟控制器包含了数量庞大且复杂的偏导数项,造成了所谓的“维数爆炸”问题,在高阶系统的控制器设计过程中该现象尤为明显,极大地增加了控制器的设计难度,导致工程上难以实现.2)鉴于递归设计需要基于Lyapunov函数的递归分析,因此无法实现稳定性分析与控制设计的本质性分离,这就容易造成设计参数或自适应更新机制选取较为复杂等问题.

为避免递归控制带来的上述问题,针对非线性系统如何能够提出一种简洁易用的非递归控制设计框架成为了近年来控制领域的热点.然而,现有文献中,值得参考的相关工作还较少.例如当系统(1)中di=0,i ∈N1→n而存在模型参数不确定时,文献[20]提出了一个自适应的输出反馈设计思路,通过引入一个自适应调节的增益函数,优化了动态性能的同时,非递归的设计框架保证了设计过程的简洁性.文献[21]提出了一个带有双层自适应参数更新机制的控制律,结合自调节预测周期,提升了控制系统的动态性能,缓解了受控系统鲁棒性冗余的问题.针对系统(1),通过结合主动抗扰技术与齐次系统理论,文献[22]提出了一个简洁有效的非递归有限时间精确跟踪控制器设计方案.文献[23]结合了神经网络和高增益干扰观测技术,实现了非递归自适应的输出反馈控制.而值得注意的是,上述文献主要是在鲁棒控制或自适应控制的单一视角下提出具体的控制设计方案,其在具有一定优势的同时,也存在一些难以解决的问题.一般而言,鲁棒控制设计步骤较为简单,但鉴于其保守的设计特性,通常在处理工况变换复杂的情况时,系统的动态性能难以得到保障.而相较于鲁棒控制,自适应控制的设计过程稍显复杂,同时响应受扰动的影响较大,但其处理复杂工况时,可以自适应调节控制带宽以优化控制系统的动态性能.那么从面向工程实用的角度来说,一个自然的猜想便是:在非递归控制的设计框架下,是否存在一种能够融合鲁棒控制与自适应控制的设计方案,可以通过切换一体化控制器的工作模式以应对各类型复杂工况? 简而言之即是:针对系统不同的复杂工况,在控制律形式完全一致的情形下,仅需要切换带宽因子的选取方式便能够得到其鲁棒或自适应控制律,并实现系统输出轨迹的精确跟踪.

为初步给出上述猜想的解决方案,本文针对系统(1),在非递归框架下,首次提出了鲁棒/自适应融合的无静差跟踪控制策略.首先采用高阶滑模干扰观测器(higher order sliding mode disturbance observer,HOSMDO)对系统不匹配干扰项的各阶导数信息进行精确估计,结合前馈补偿技术实现在有限时间内恢复不匹配受扰系统的性能;其次,通过求解一系列输出调节方程及巧妙设计状态变换函数,给出系统化的非递归复合控制构建框架;随后,分别在不同类型的工况下给出带宽因子的配置方案,即对应鲁棒/自适应控制律;最后,基于半全局稳定性目标,本文分别给出了鲁棒情形及自适应情形下闭环系统严格的稳定性分析.相较于现有的相关方案,本文的主要贡献可以概括为:

1) 结合前馈补偿与反馈控制的设计思路,通过仅一步的坐标变换,本质实现了同框架下鲁棒/自适应融合的一体化控制器构建.

2) 基于非递归控制设计框架,使控制器设计过程与稳定性分析分离开来,本质上避免了递归控制方法中常见的“维数爆炸”的问题.同时,控制参数选取有简洁明确的指导机制,更易于工程实现.

2 问题描述

本文旨在提出1个鲁棒/自适应融合的非递归复合控制律,实现系统(1)的无静差轨迹跟踪控制目标,即首先,针对系统(1)做如下假设.

假设1输出参考信号yr及其n阶导数都是分段连续,完全已知且有界的.

假设2干扰di(t)满足i ∈N1→n,j ∈N0→n−i+1,且D是一个正常数.

本文所提控制器是基于基准控制律u=U(L,K,x,x∗),切换带宽因子的选取法则,具体表述为

其中:K为系统的控制参数,x∗=为系统的稳态参考信号,为与系统非线性项相关的中间估计量,L(·),ψ(·)为两个恒正的函数,具体表达式将在文章后续给出.L0表示带宽因子L的初始值.

3 非递归跟踪控制律设计

本节将逐步给出所提非递归融合控制器构建步骤.

3.1 预处理

假设系统(1)中的干扰项di完全已知且给定参考输出yr时,定义辅助状态变量=(ς1ς2··· ςi)T,i ∈N1→n+1,ςi满足以下等式:

注1值得一提的是现有文献中有诸多干扰观测器用以实现干扰软测量,如非线性干扰观测器(nonlinear disturbance observer,NDO),扩张状态观测器(extended state observer,ESO),广义比例积分观测器(generalized proportional integral observer,GPIO)等.与这些观测器相比,本文所采用的HOSMDO仅需满足假设2,而无需对干扰外源模型进行辨识,即可在有限时间内获取系统干扰及其高阶导数的精确估计信息,便于后续设计的精确前馈解耦,从而有效地提高了闭环系统的收敛速度及跟踪精度.

3.2 坐标变换

为了引入非递归控制框架,结合高增益控制技术,作如下形式的坐标变换:

其中:L可以是正常数,也可以是一个满足L0=1,˙L≥0的函数,其设计规则在后续控制设计过程中给出,ϱ>0为设计参数,υ为中间控制器.

考虑L为动态增益时,定义矩阵P=PT>0,且(A −BK)TP+P(A −BK)≤−In,其中(A,B)为可控标准型矩阵对,K=(k1,k2···kn)是Hurwitz多项式H(s)=sn+knsn−1+···+k1的对应系数,In为n阶单位阵,Θ≜diag{0,1,···,n −1}.ϱ满足如下约束条件:

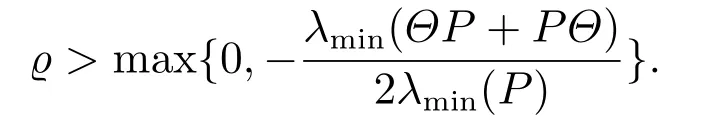
根据式(6),可得如下与式(1)等价的系统形式:

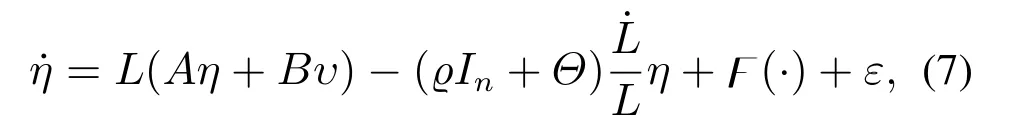
其中:

当L为静态增益时,即式(7)中=0,L为一个充分大的定常带宽因子,此时ϱ可以为任意正常数,同样地,可以得出下列与式(1)等价的系统形式:

3.3 控制器形式

至此,无需递归化Lyapunov函数设计,本文已经能够给出系统(1)的非递归控制律.具体地,具有鲁棒/自适应一体化融合结构的非递归控制器可以表述为如下形式,其设计流程可见于图1.

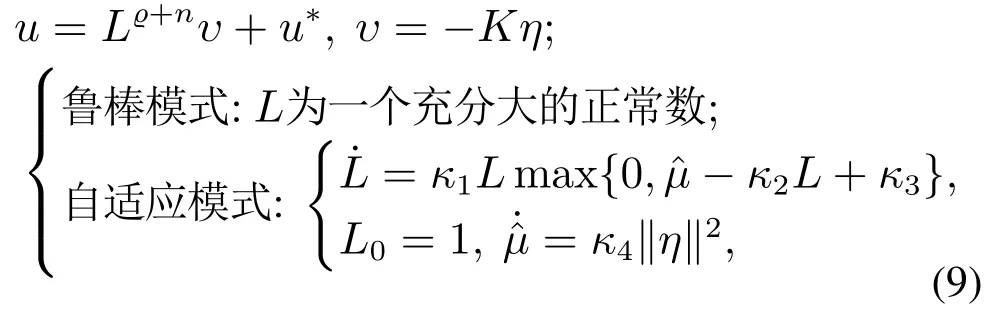
其详细证明可见于附录.

注2显而易见地,所提非递归鲁棒/自适应融合控制是建立在同一个变换下,根据一步法提出的前馈补偿加反馈控制结合的输出调节控制策略,做到了控制器设计与稳定性分析的本质分离.值得一提地,非递归自适应控制通过采用具有自调节能力的带宽增益函数,实现控制系统在不同工况下能够达到无静差跟踪控制目标,进一步改进了控制器参数选取机制.

4 数值与实例仿真对比分析

4.1 数值仿真

本文首先考虑一个简单的二阶系统,其表达式如下所示:

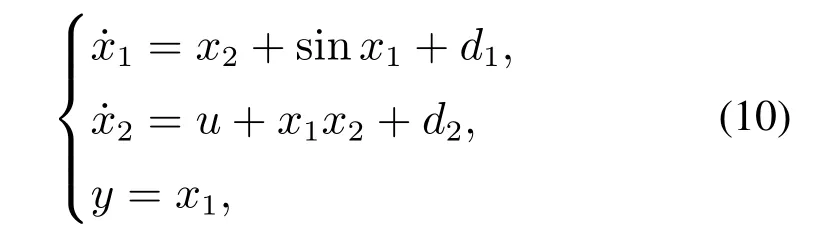
其中d1,d2分别为系统的不匹配干扰与匹配干扰.为实现该系统的跟踪控制目标,文献[19]通过将非线性干扰观测器与反步法相结合,提出一个主动抗干扰控制策略,其核心思想是将干扰估计值引入虚拟控制器的每一步设计过程中,在递归地弥补受扰系统性能的同时,实现高精度跟踪控制目标.基于该文方法,其复合控制器可被表述为以下形式:

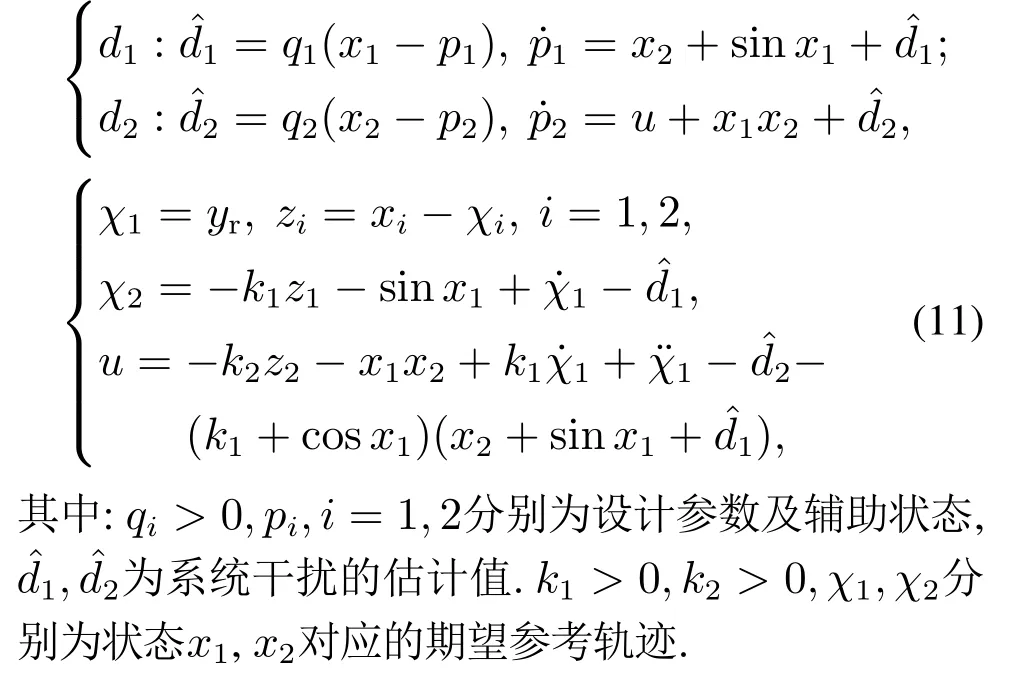
随后,由所提的非递归一体化复合控制设计框架,首先利用HOSMDO对干扰进行估计,具体可描述为

随后在控制器(12)形式保持不变的情况下,将L设计为动态模式,可以得到非递归自适应控制的双层动态更新机制,具体可以表述为如下形式:

在后续仿真中,通过设定yr=1+0.5 cos(t+π/4)并选取干扰动态为d1=sin(0.5t+π/3),d2=cost+sin(0.5t),分别使用两种不同的控制策略(递归与非递归算法),可以得到如下的仿真结果,如图2(a)(b)所示.其中递归控制器参数为:[k1,k2,q1,q2]=[6,10,28,32].非递归控制器参数为:高阶滑模干扰观测器参数:[l1,0,l1,1,l1,2,λ1]=[12,13,14,1],[l2,0,l2,1,λ2]=[12,13,1].鲁棒控制器参数:[k1,k2,L,ϱ]=[25,18,3,1].自适应控制器参数:[k1,k2,ϱ]=[25,18,1].

从图2(a)(b)可以看出,两种控制策略都可以实现系统(10)的精确跟踪控制目标.而值得关注的是:通过比较式(11)与式(12)–(13),可以清晰地看出控制律(12)–(13)具有更为简洁的形式,且非递归控制器主要依赖与系统的标称模型,而非线性项及其偏微分项等并不直接体现在控制律中,这与反步法等递归控制算法具有本质的区别.

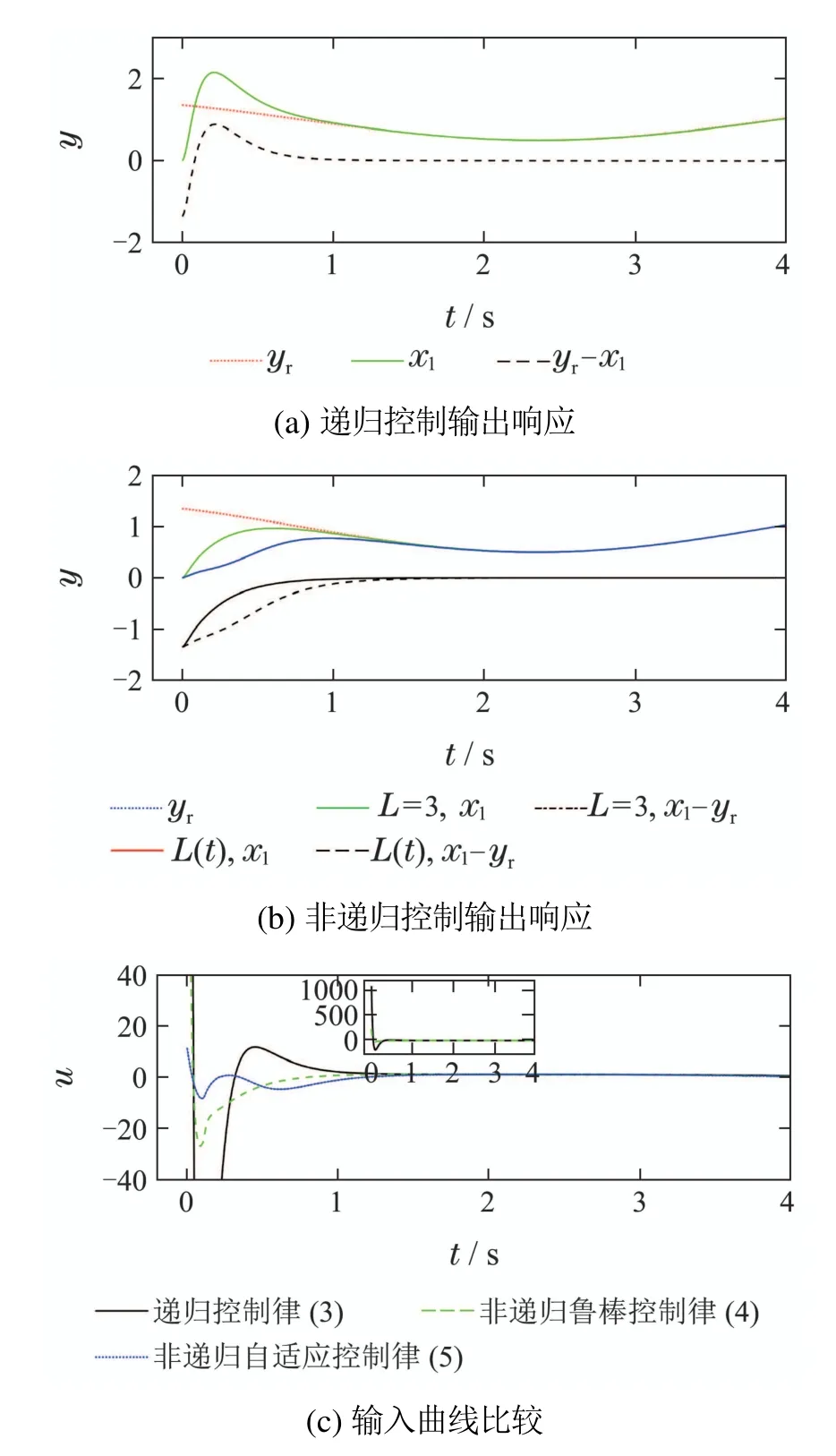
图2 递归控制与非递归控制的输出响应及控制输入曲线Fig.2 The output responses and control inputs of system controlled by recursive control law and non-recursive

4.2 实例仿真

本小节考虑一个单连杆机械手的无静差跟踪控制问题,用以阐明所提控制器的有效性.其具体包含了机电动态和干扰项,动态方程可表述为[25]

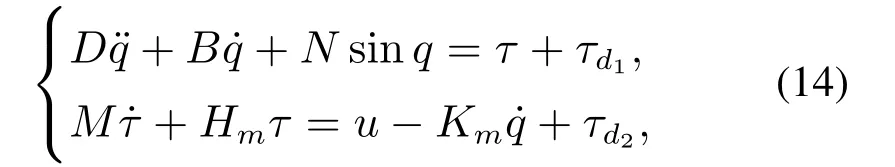
其中:q,,分别代表连接位置,速度及加速度.τ是由电气系统产生的扭矩,τd1对应着扭矩干扰,为系统可测数据的测量误差,u是系统的控制输入,通常是指机电扭矩.D=1 kg·m2是机械惯量.B=1 N·m·s·rad−1为粘性摩擦系数.N=10 是一个正常数,其值与载荷质量与重力系数相关.M=1 H为电枢电抗.Hm=1.0 Ω 是电枢电阻.Km=0.2 N·m·A−1为反电动势系数.

接下来,令x1=q,x2=,x3=τ,那么系统(14)可被改写成下面的形式:

根据图3和图5可以清晰地看出,本文所提的控制器可以保证系统全状态对应地无静差跟踪至其预期参考信号进一步地,通过对不同幅值的干扰进行比较,阐明了所提的非递归自适应控制器的增益更新机制,对于系统所受的大小信号干扰,L收敛的上界也会发生变化,这是由系统状态轨迹与参考轨迹的误差大小不同导致的,小信号干扰使上述误差相对小,L的收敛值为2.18左右;而随着干扰信号增大,L的收敛值又随之变为了2.48 左右;而对于一个幅值在二者之间的时变干扰,增益L又收敛至2.2左右.图5(d)则表明相较于非递归鲁棒控制,非递归自适应控制可以在消耗较低控制能量的情形下,即实现系统的控制目标.

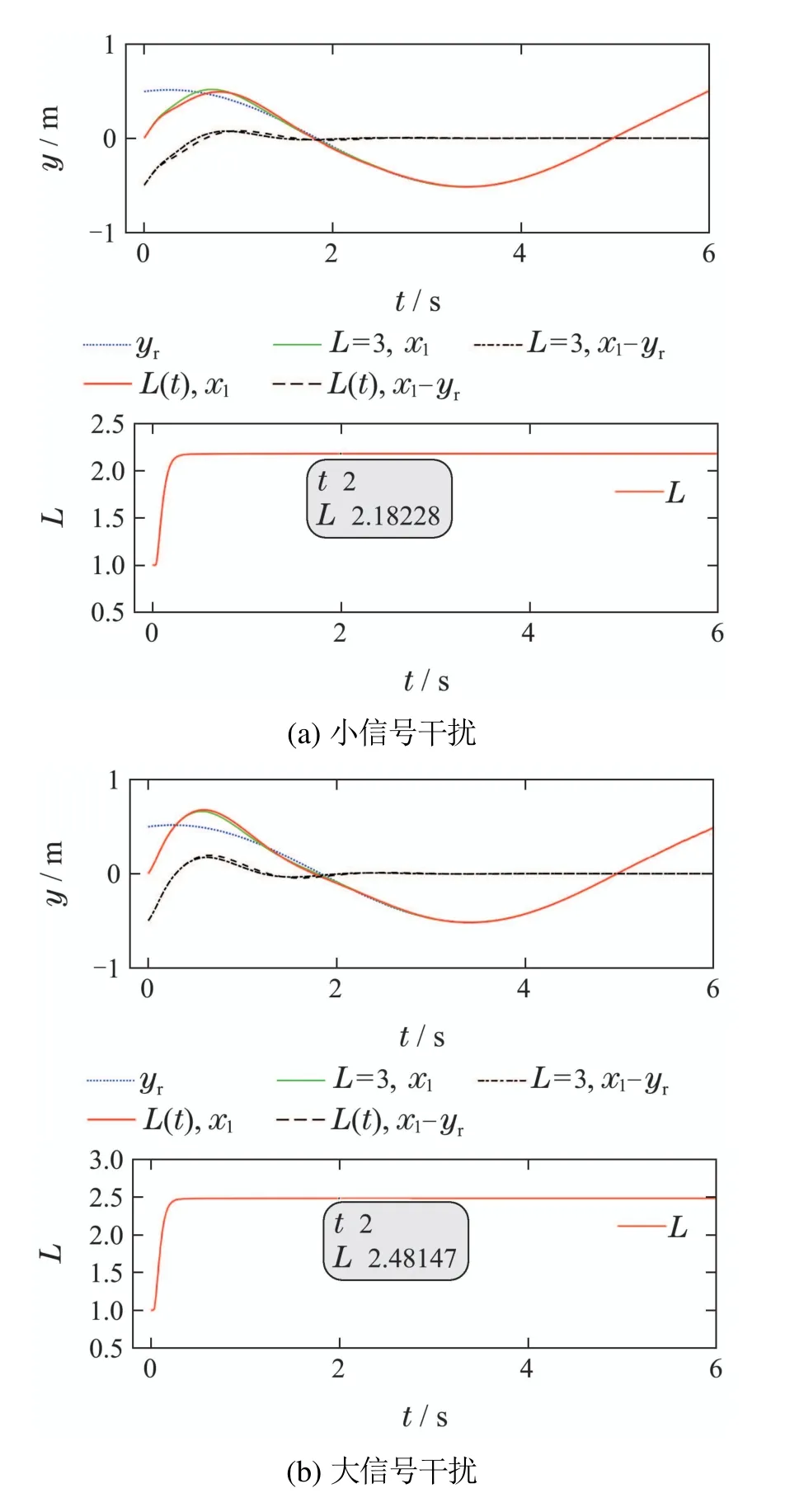
图3 常值干扰下单连杆机械手系统Fig.3 The response curves of one-link manipulator with constant disturbance cases

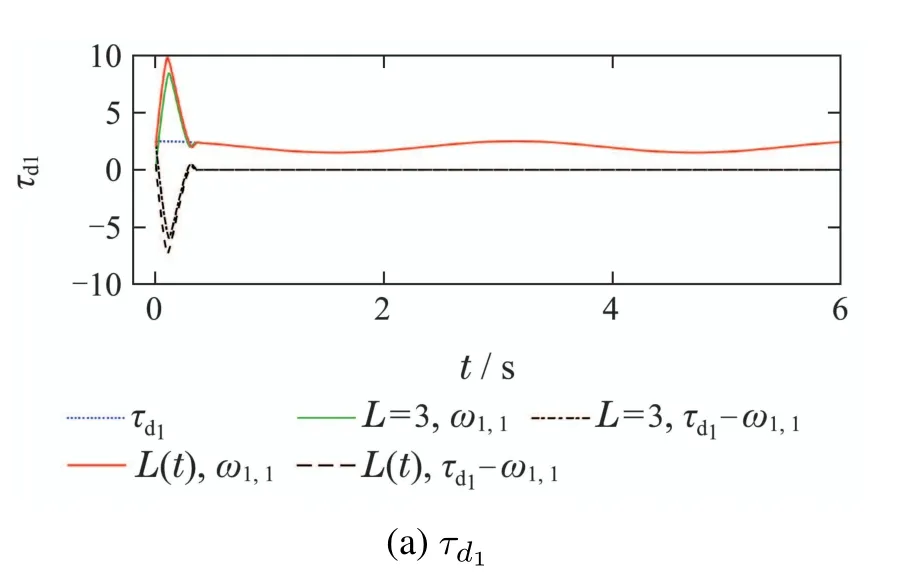
图4 单连杆机械手系统时变干扰信号曲线Fig.4 The time-varying disturbance curves of one-link manipulator

图5 时变干扰情况下单连杆机械手系统Fig.5 The state curves of one-link manipulator with time-varying disturbance case

注3对于参数选取,主要可遵循以下几个原则或步骤:1)通过极点配置得出控制增益K,将闭环系统的极点配置至期望极点处.2)求线性矩阵不等式(A −BK)TP+P(A−BK)≤−In,从而获取正定对称阵P.3)根据参数ϱ的选取准则,确定其范围.κ1,κ2,κ3,κ4则根据其对应的选取准则求出范围,并通过“试错法”,选取满足性能指标要求的值.4)鲁棒控制的增益L满足充分大的条件,但是需要指出的是,随着L的增大,系统可能会出现鲁棒性冗余.因此,类似地使用“试错法”,选择满足性能要求的L值.自适应控制情形下,L可在不同实际工况下自适应地收敛于不同的值,以此来缓解控制增益选取过大带来的鲁棒性冗余,并且提升控制系统的动态性能.

5 总结

本文主要提出了一种针对含不匹配干扰的非线性系统的鲁棒/自适应一体化非递归控制设计框架.相较于以往的结果,该非递归复合控制框架有以下的几点贡献:首先,所提复合控制律具有更为简洁的表达形式和一定的可移植性,非线性项约束条件也更为宽松,设计思路更加多元.一步法的设计框架将控制器设计与稳定性分析本质性分离开,极大地方便了工程实际应用.未来旨在解决多类型的非线性系统的跟踪问题,例如对于离散系统、状态受限的非线性系统等,运用本文所提控制框架,如何实现精确跟踪.

附录

为便于后续的稳定性证明,首先提供一下引理.

紧接着,将对状态η的有界性进行阐述.即是证明对于任意非零的初始状态满足η∗(0)∈Ωη∗,任意η(t)的轨迹将在Ω内.

为了更好地阐述,假设η(t)在系统渐近稳定过程中出现逃逸.那么根据有限时间逃逸理论,存在一个时刻t1≥0,使得