自抗扰控制对边界带有干扰的非线性sine-Gordon方程的镇定

周华成

(中南大学数学与统计学院,湖南长沙 410083)

1 引言

带干扰的偏微分方程镇定问题是分布参数系统控制理论研究的重要内容之一.近年来许多控制方法如滑模控制、自适应控制、自抗扰控制等方法被人们大量的应用到这类问题研究中.中国科学院韩京清先生在文献[1]中提出自抗扰控制方法,主要思想是设计扩张状态观测器估计干扰并实时消除干扰,这是一种旨在对付系统大不确定性的新的控制理论,在工业控制中显示出巨大的潜力应用(参见文献[2–4]).文献[5]首次把自抗扰控制用于一维的波动方程中,随后应用到Euler-Bernoulli 梁方程[6]和Schr¨odinger方程[7].文献[5–7]采用的策略是把偏微分方程中的边界扰动通过试验函数转换成带扰动的常微分系统,从而可以直接应用文献[1]中的自抗扰扩展观测器设计.对于高维偏微分方程系统,文献[8–9]提供了结合时变覆盖和逐点估计的自抗扰方法,获得高维波动方程和Kirchhoff板方程的稳定性结果.最近的输出反馈控制进展是基于不连续控制设计和基于无穷维扩展状态观测器,文献[10–11]给出了一维波动方程的渐近稳定性,文献[12–13]给出了一维波动方程的指数稳定性,文献[14–15]获得了Euler-Bernoulli梁的指数稳定性,而高维波动方程输出反馈渐近稳定性可参见文献[16].需要指出的是文献[10]提出的无穷维扩展状态观测器是一种革新的处理干扰方法,近期获得了极大的发展,如一维波动方程性能输出调节[17–18],一维热方程性能输出[19]和高维热方程的性能输出[20].

注意到文献[5–7,10–14,16,21]讨论的受控偏微分方程系统在不带扰动时都是线性系统,而当受控偏微分系统本身就是非线性时,处理不确定扰动尤为困难,文献[22]给出了sine-Gordon方程含有调和干扰的自适应控制方法并获得渐近稳定性例子.由于sine-Gordon方程的非线性,自文献[22]之后,据笔者所知,尚未有新的关于带干扰的非线性偏微分系统稳定性结果.受文献[22]启发,本文利用自抗扰控制方法处理边界含有内部不确定和外部扰动的非线性偏微分的镇定问题.

考虑如下具有非线性项的sine-Gordon方程

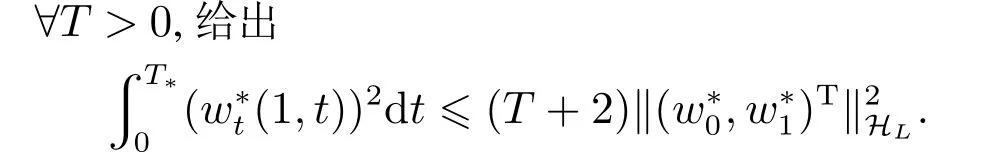
因此控制算子B2对半群eAt是可允许的.根据引理1,开环系统(1)存在唯一解(w,wt)∈C(0,∞;HL).证毕.

2 控制器设计

为了能够消除干扰,笔者首先为系统(1)设计无穷维总扰动估计器如下:

其中(z0,z1,v0,v1)是系统(5)的初值,可以任意选取.可调参数c1,c2是两个大于零的正常数.“z–子系统”用来把总扰动F(t)=f(w(·,t),wt(·,t))+d(t)从受控系统(1)中分离,并带入到一个指数稳定的系统中去.事实上,令

直接验证可知p(x,t)满足如下偏微分方程:

为证明系统(6)的适定性和有界性,本文参考文献[12]中的引理2.

引理2假设U1,U2,X是3个Hilbert空间.算子A在Hilbert空间X中生成指数稳定的C0半群eAt,算子B1∈L(U1,X−1),B2∈L(U2,X−1)是两个对半群eAt可允许的控制算子.则初值问题

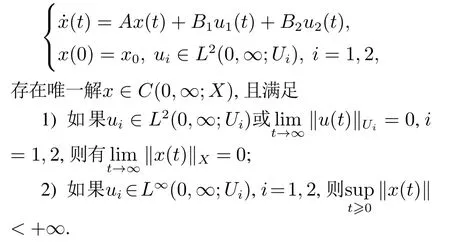
引理3假设外部干扰d ∈L∞[0,∞),内部不确定f ∈C(HL,R),使得系统(1)存在唯一解并且是有界的.则对任意初值(p0,p1)T∈H,系统(6)存在唯一解(p,pt)T∈C(0,∞;H)并且

在控制律(16)中,−kwt(1,t)是用来镇定系统,vx(1,t)+c2v(1,t)是用来补偿(取消)总扰动,这一步是自抗扰控制的取消补偿思想[1].

最后,由式(5)和式(16)可得到sine-Gordon系统(1)的闭环系统:

在Hilbert空间X=HL×H2中考虑系统(17).

3 闭环系统适定性和稳定性

为证明闭环系统(17)的适定性和稳定性,首先考虑如下系统:

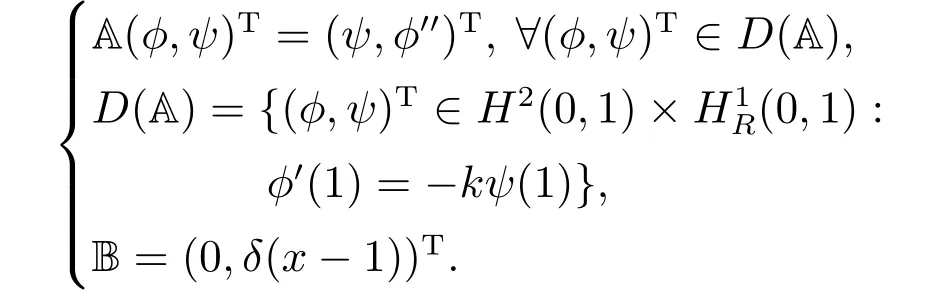
注意到sin(w(·,t))满足全局Lipschitz条件,再根据引理1,可知系统(18)的“w–子系统”存在唯一解.因此闭环系统(18)存在唯一解.

第2步证明指数稳定性.

定义Lyapunov 泛函V(t)=V1(t)+V2(t),其中V1(t)和V2(t)分别为

由此,再根据引理4和β ∈(−π2/4,π2/4),可以得知引理5结论成立. 证毕.

注1如果β=0,可以根据引理4和文献[12]中的引理2.1,直接获得系统(19)的指数稳定性.在引理5的证明中,由于sine-Gordon方程中非线性项βsin(w(x,t)),指数稳定性不能直接由引理4和文献[12]中的引理2.1获得,本文采用Lyapunov方法证明系统(19)的指数稳定性.

证利用p(x,t)=z(x,t)−w(x,t)和q(x,t)=v(x,t)+p(x,t),可以将闭环系统(17)等价的转换为如下系统:

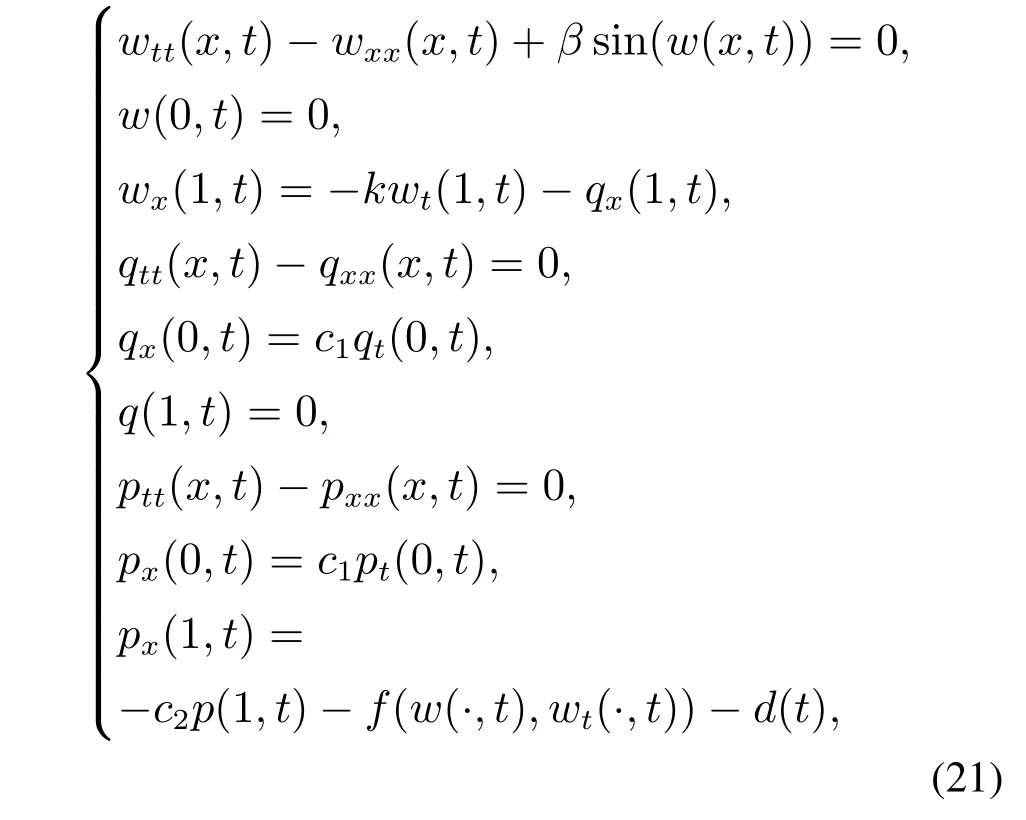
系统(17)的适定性等价与系统(21)的适定性.“(w,q)–子系统”独立于“p–子系统”.根据引理5,“(w,q)–子系统”存在唯一解,并且存在常数M1,µ1>0满足

注2在定理1中,仅假设内部不确定扰动f是(0,1)×L2(0,1)中的连续泛函,因此去掉了命题1中关于f满足全局Lipschitz的条件.这是由于通过设计总扰动估计器(5),把非线性总扰动F(t)巧妙地从受控系统(1)中分离,并将带入到指数稳定的系统中.

注3根据定理1的证明可知,当β=0时,定理1的结论仍然成立.此时sine-Gordon方程退化为经典的波动方程.对这个经典的波动方程,不需要测量全部状态,只需要测量边界x=0处的力wx(0,t)和x=1处的位移和速度{w(1,t),wt(1,t)}.相比文献[21]中的结果(文献[21]中量测是wt(1,t),w(x,t),x ∈[0,1],而结论是渐近稳定),本文量测是{wx(0,t),w(1,t),wt(1,t)},得到指数镇定结果.当β=0时,只需要测量边界x=0处的力wx(0,t)和x=1处的位移w(1,t)的指数稳定方法可参见综述文献[24].

4 数值模拟

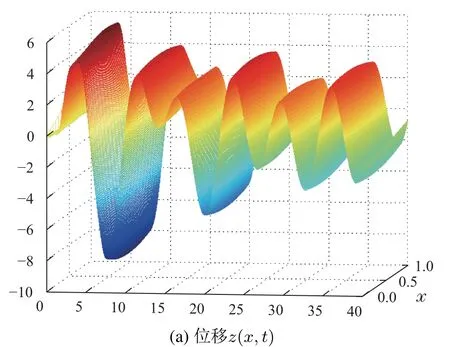
对闭环系统(17)进行数值模拟.系统参数选取β=0.1,k=2,c1=1,c2=2,内部模型不确定f(w(·,t),wt(·,t))=sin(w(0.5,t)),外部扰动为d(t)=2 sint.系统的初值选取w(x,0)=2x −x2,wt(x,0)=−2x+x2,v(x,0)=vt(x,0)=z(x,0)=zt(x,0)=0.从数值仿真图1可以看出(w,wt)收敛很快,图2和图3看出(v,vt,z,zt)是有界的.图4是总扰动和控制u(t),可以看出在t=15后完全补偿了扰动F(t).因此数值仿真表明本文方法非常有效.

图1 系统(17)的w–子系统的位移和速度Fig.1 The displacement and the velocity of w-subsystem of system(17)

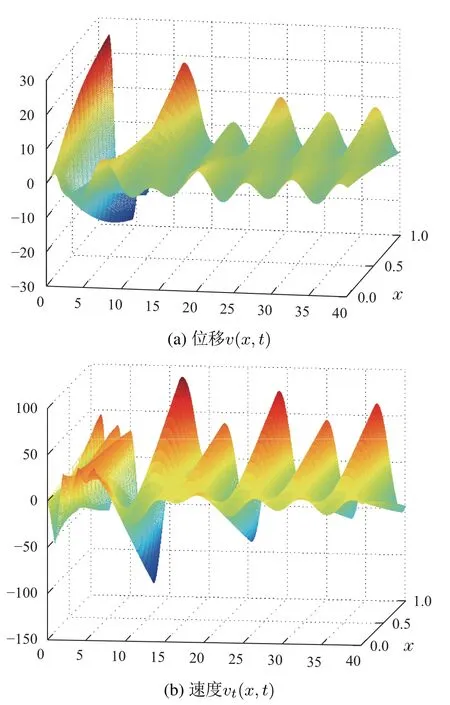
图2 系统(17)的v–子系统的位移和速度Fig.2 The displacement and the velocity of v-subsystem of system(17)

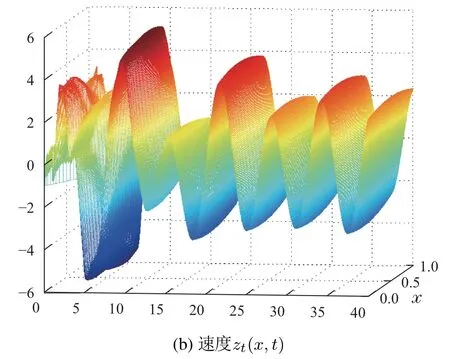
图3 系统(17)的z–子系统的位移和速度Fig.3 The displacement and the velocity of z-subsystem of system(17)

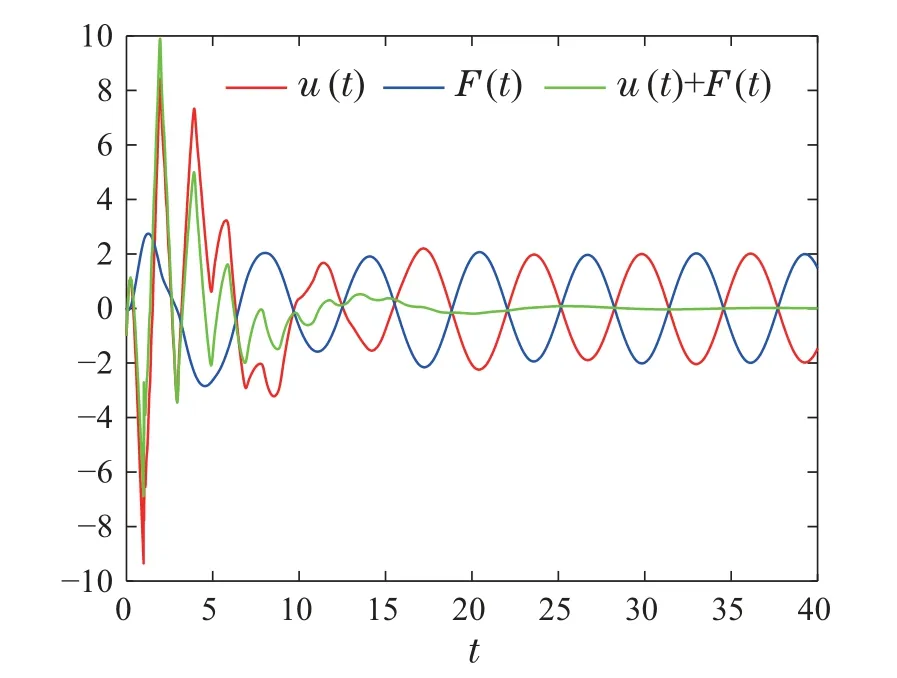
图4 系统(17)的总扰动和控制u(t)Fig.4 The total disturbance and the control u(t) of system(17)

5 结论

本文通过针对具有内部不确定和外部扰动的非线性sine-Gordon方程,利用自抗扰方法设计了总扰动观测器在线估计未知总扰动,使用总扰动的估计值在闭环反馈中实时补偿(消除),同时借助于Lyapunov方法证明闭环中的受控系统的指数稳定性和扰动观测器是有界性,最后通过数值仿真验证控制设计的有效性.对非线性偏微分系统自抗扰仍有很多问题有待研究,如可考虑输出反馈控制和输出跟踪问题.