考虑排水体系时隧道突涌水分析
傅鹤林,安鹏涛,伍毅敏,成国文
(1.中南大学 土木工程学院,湖南 长沙 410075;2.广东省南粤交通投资建设有限公司,广东 广州 510101)
富水区隧道施工可视为人为对围岩渗透系数及渗流边界的改变,若超过一定界限,地下水将威胁其整个建设过程及服务期,破坏隧址区生态文明,降低结构稳定性[1−3]。综合考虑安全、环保及经济因素,富水区隧道防排水设计多采用“以堵为主,限量排放”的准则[4−6]。此时涌水量及渗水压力的计算对结构设计及施工十分重要[7−9]。李杰等[10−13]在忽略支护结构内缘承担水头的假定下,基于地下水力学理论及达西定律,揭示了注浆参数对深埋隧道附近渗流场的影响规律,为注浆圈的设计提供了理论基础。何本国等[14−15]探讨了排水体系对隧道涌水及结构承担水头的影响机理,为富水区隧道排水体系的设计提供了指导。ARJNOI等[16−17]借助数值计算手段分析了渗流场与支护结构水压力的分布规律。理论分析时,学者均忽略了支护结构内缘承担的水头,导致现有解析公式与实际存在一定差距[14,18]。事实上,初期支护背后依次有土工布、环向排水盲管及防水板,防水板使得二次支护结构本身并不发生渗流,土工布内的渗流是沿隧道轴向的一维流[19]。为此,构建考虑支护结构内缘承担水头的深埋隧道涌水简化计算模型,基于地下水力学理论及达西定律推导涌水量及结构外缘承担水头的计算式,通过退化分析及工程案例检验涌水简化计算模型构建的有效性及公式推导的正确性。在此基础上对特征参数进行敏感性分析,揭示各结构及排水体系对隧道涌水的影响机制,以求对考虑支护结构内缘承担水头时隧道涌水的机理进行有意义的尝试与探索。
1 问题分析与基本假定
隧道开挖改变了原岩的渗透系数及边界条件,引发地下水能量的释放,理论上开挖区渗透系数趋于无穷大。事实上,隧道洞身、支护结构、注浆圈及扰动区均可视为人为对围岩性质的干涉,使原岩渗透系数升高或降低。设计或施工不当,将破坏原来处于相对稳定的地下水系统,进而发生涌水突泥事故。考虑实际工况及方便问题解答,作如下假定[22]。
1) 流体不可压缩;
2) 渗流服从达西定律;
3) 渗流处于稳定状态;
4) 隧道为大埋深。
人为干涉下,构建深埋隧道涌水简化计算模型,如图1所示。
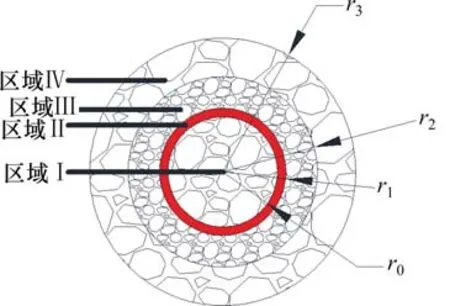
图1 涌水简化计算模型Fig.1 Simplified calculation model of water inflow
图1中,各区域渗透系数在扰动前均为kr,外缘半径分别为:r0,r1,r2及r3;区域Ⅰ开挖后渗透系数为k′r,其值趋于无穷大;区域Ⅱ为隧道支护结构,渗透系数为ks;区域Ⅲ为注浆圈或开挖损伤区,渗透系数为kⅢ;区域Ⅳ为原岩。
2 涌水量及结构外水压力计算
据假定,渗流满足达西定律,表达式为[23]

式中:v为渗流速度;k为介质渗透系数;i为水力坡度。
以无限含水层中的竖井理论进行分析,据地下水力学理论,由竖井推导的结论对隧道完全适用[24]。依次计算各区域渗流场,利用边界条件计算隧道涌水量及各区域外缘承担的水头。据地下水力学理论
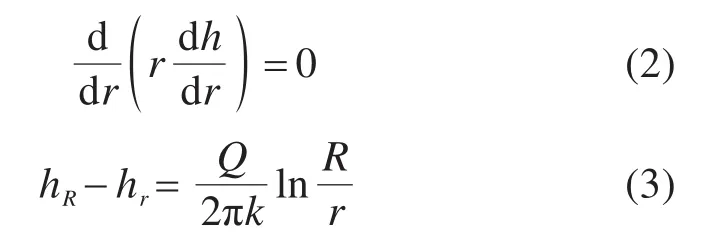
式中:Q为每延米洞身涌水量;R及r为地层中距孔洞中心任意两点的半径;hR及hr为R与r处的水头。
开挖前,区域Ⅰ可视为开挖孔径无穷小且内边界水头与初始水头相等的区域。此时水力梯度、涌水量及渗流速度均为0,各区域外缘承担的水头与初始水头相等。隧道开挖后,区域Ⅰ及Ⅳ边界存在水头差,将式(3)依次应用于区域Ⅳ,Ⅲ及Ⅱ得
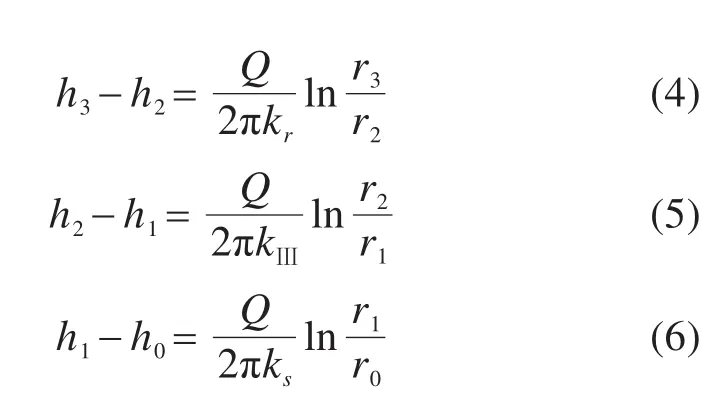
由式(4)~(6)可得
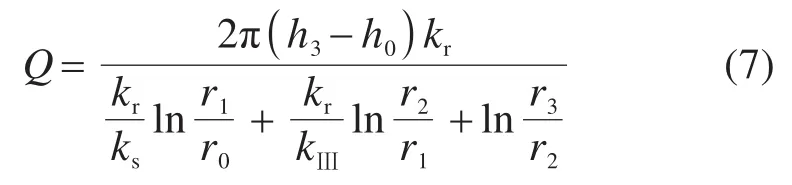
为便于对支护结构设计,将区域Ⅲ及Ⅱ视为整体,其等效渗透系数为kb。渗流稳定时为保证涌水量相等,等效渗透系数计算式为
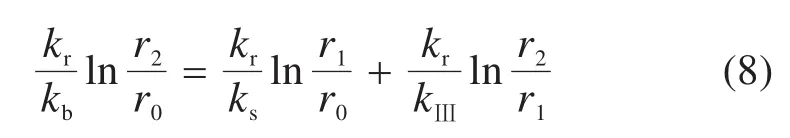
化简得
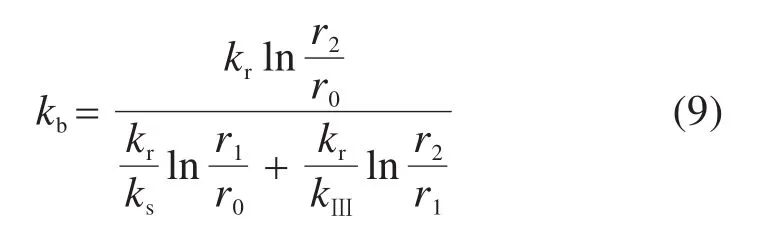
由文献[25]可知,支护结构内缘承担的水头沿隧道轴向呈抛物线分布,平均值计算式为
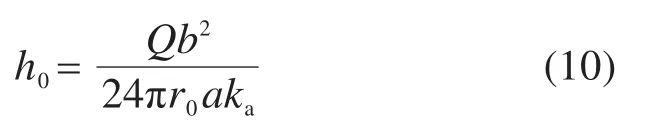
式中:a为土工布厚度;b为环向盲管间距;ka为土工布渗透系数。
联立式(7)及(9)~(10),解得涌水量计算式为
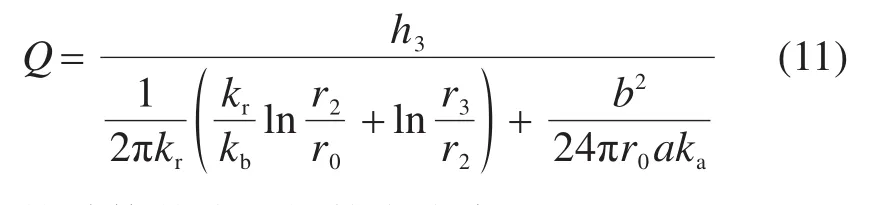
支护结构外缘承担的水头为
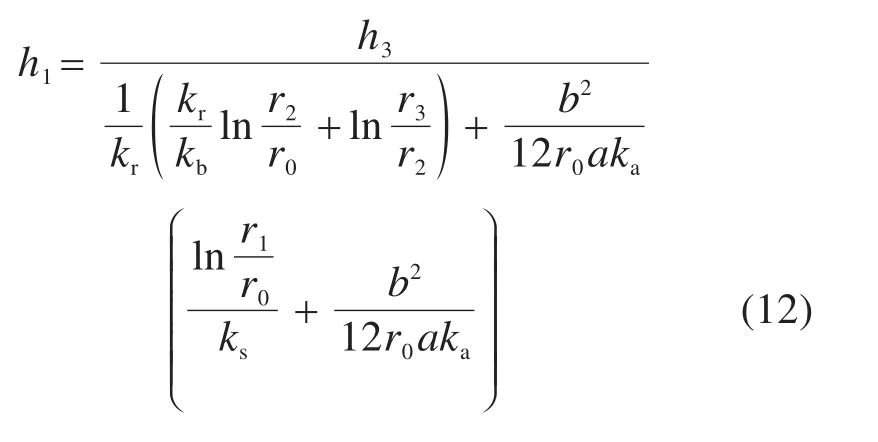
据式(11)和式(12),可对富水区隧道防排水系统及结构进行设计。
3 结果验证
3.1 退化分析
不考虑土工布的布设,环向盲管位置渗透系数趋于无穷大,此时式(11)退化为
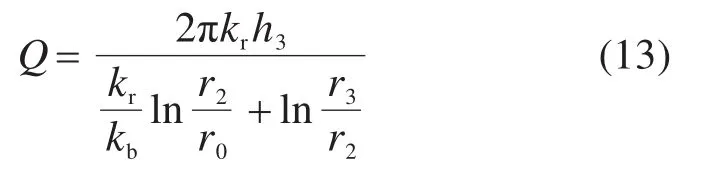
将式(9)代入式(13),得
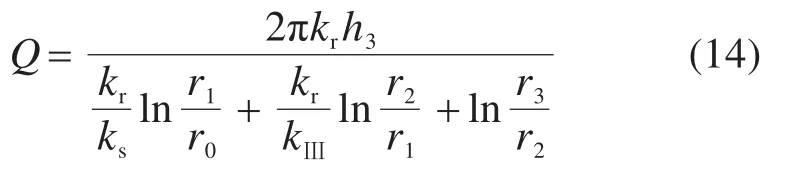
式(14)与文献[26]计算结果相同,表明式(11)可退化为不考虑支护结构内缘承受水头时隧道涌水量计算式。同时文献[27]在计算毛洞涌水量时具有较高的准确度,不考虑注浆、开挖扰动及支护结构时,有r2=r1=r0,此时式(14)可进一步退化为

式(15)为古德曼方程计算毛洞涌水量的解析公式。
不考虑支护结构内缘承受的水头时本文推导的隧道涌水量计算式(11)可退化到文献[26]所建立的公式。不考虑开挖扰动、注浆圈及支护结构时,本文所推导的公式与文献[26]所建立的公式均可退化到文献[27]所推导的开挖隧道后最大涌水量计算公式。初步验证了本文构建的深埋隧道涌水简化计算模型的合理性及隧道涌水量计算式推导的正确性。
3.2 工程案例
依托鸿图隧道在建工程进行现场试验,实时监测涌水量及支护结构承担的水头以进一步验证本文推导的隧道涌水量计算公式的有效性。
3.2.1 工程背景
鸿图隧道位于广东省莲花山断裂带,长6 336 m,地面标高345~1 060 m,隧道底部设计标高239~344 m,最大埋深约739 m,为深埋特长公路隧道。隧址区地表分布众多水系,部分断层与大型水体相连,施工期突涌水风险极高。
3.2.2 试验方案
选取试验段,在相应里程桩号埋设智能弦式数码渗压计,现场埋设与测量如图2所示。

图2 传感器埋设与测量Fig.2 Sensor burying and measurement
测量由横向排水管流入隧道排水沟的水量,如图3所示。

图3 涌水量测量Fig.3 Water inflow measurement
3.2.3 参数选取
考虑到保角变换的局限性及复杂性[28−30],采用等代圆法将非圆形隧道断面映射为圆形,表达式为[31]
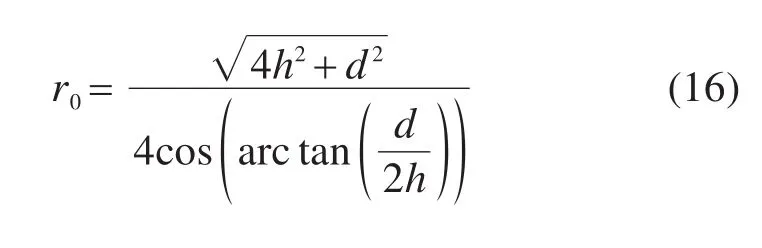
式中:d为原隧道的断面跨度;h为原隧道的断面高度。
计算得等代圆半径r0为6.2 m;初期支护与二次衬砌厚度分别为30 cm及50 cm;围岩渗透系数为1.4×10-6m/s,围岩与注浆圈及初期支护渗透系数比值分别为20与600;注浆圈厚度为5 m;地下水初始水位线由菌类分析并实施同位素追踪试验获取,为220 m;环向排水管间距为3 m;土工布厚度为4 mm,渗透系数为2×10-5m/s。
3.2.4 结果分析
忽略支护结构内缘承担的水头,由式(14)计算得隧道涌水量为2.35 m3/(d∙m);由本文推导式(11)计算涌水量为2.27 m3/(d∙m);实测涌水量为2.14 m3/(d∙m)。考虑环向排水管的作用时,本文推导的涌水量理论解与实测值的误差为6.1%,忽略支护结构内缘承担的水头时,误差为9.8%。即考虑支护结构内缘承担的水头时,涌水量计算误差可由9.8%降为6.1%,进一步验证了本文构建的深埋隧道涌水简化计算模型的有效性及涌水量预测计算式推导的正确性。预测误差主要有等代圆的近似代替及围岩渗透系数的离散性。
4 参数分析
考虑到隧道涌水量及支护结构承担水头计算式影响因素的复杂性,为揭示其影响机制,假定r0及r3分别为6 m及200 m;地下水水位线距隧道中心竖直距离为100 m;围岩渗透系数为5×10-6m/s,围岩与土工布渗透系数比值为1/40;土工布厚度为5 mm。对各特征参数进行敏感性分析。
4.1 区域Ⅲ
进一步假定r1为6.8 m;围岩与支护结构渗透系数比值为800。未实施帷幕注浆时,区域Ⅲ为扰动区,其渗透系数较原岩增加。为保护地下水及隧道支护结构,常施作注浆圈,此时渗透系数降低。原岩渗透系数与区域Ⅲ渗透系数比值为m,计算区域Ⅲ与涌水量的关系,绘制曲线如图4所示。
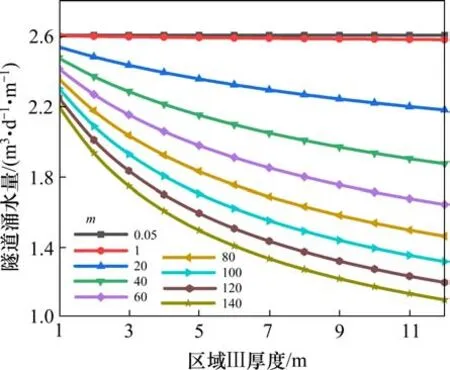
图4 隧道涌水量与区域Ⅲ的关系Fig.4 Relationship between tunnel water inflow and Area III
图4显示,渗流稳定时隧道涌水量对区域Ⅲ渗透系数的敏感性随渗透系数的降低而逐渐减弱。适当提高区域Ⅲ的抗渗性能可有效降低隧道涌水量,但随区域Ⅲ抗渗性能的增加,对隧道涌水量降低的作用逐渐趋于平缓。区域Ⅲ厚度对隧道涌水量的影响与渗透系数相似,注浆设计时须对注浆圈厚度及渗透系数进行合理取值。考虑扰动时,区域Ⅲ渗透系数的增加对隧道涌水量的影响较弱,原因为支护结构渗透性较弱,为主要的堵水介质。
计算区域Ⅲ与支护结构承担水头的关系,绘制曲线如图5所示。
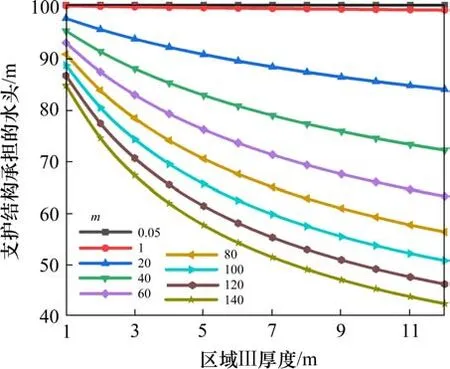
图5 隧道支护结构承担的水头与区域Ⅲ的关系Fig.5 Relationship between water head borne by tunnel support structure and Area III
图5显示,渗流稳定时区域III渗透系数对支护结构承担水头的影响规律与涌水量相似。人为干预下,区域III渗透系数下降可降低隧道涌水量及支护结构承担的水头,表明富水条件下帷幕注浆的设计是必要且有效的。
4.2 区域Ⅱ
假定区域Ⅲ厚度为6 m;围岩与其渗透系数比值为40。区域Ⅱ为支护结构,其渗透系数较原岩大幅降低。计算区域Ⅱ与涌水量的关系,绘制曲线如图6所示。
图6表明,渗流稳定时隧道涌水量随区域Ⅱ渗透系数的降低及支护结构厚度的增加而不断减小,但敏感性逐渐减弱。
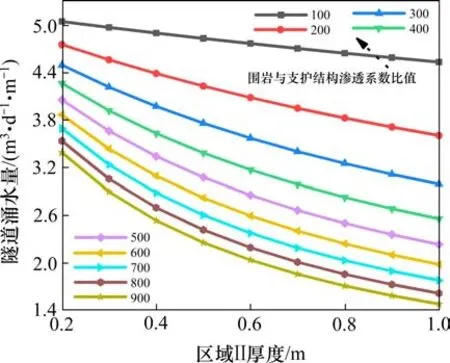
图6 隧道涌水量与区域Ⅱ的关系Fig.6 Relationship between tunnel water inflow and Area Ⅱ
计算区域Ⅱ与支护结构承担水头的关系,绘制曲线如图7所示。
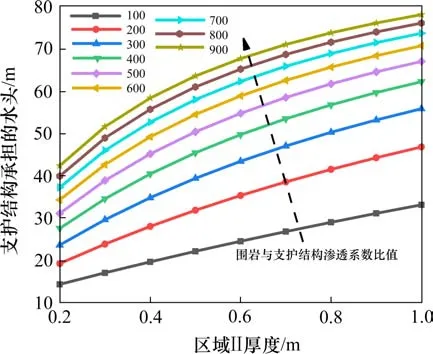
图7 隧道支护结构承担的水头与区域Ⅱ的关系Fig.7 Relationship between water head borne by tunnel support structure and Area Ⅱ
图7表明,渗流稳定时支护结构外缘承担的水头随区域Ⅱ渗透系数的降低及支护结构厚度的增加而不断增加,其敏感性同样逐渐减弱。
图6和图7表明区域Ⅱ的厚度及渗透系数的设计须综合考虑,其值的确定受支护结构承担的水头与隧道涌水量相互制约。若单独设置区域Ⅱ无法同时满足受力及控制涌水的目的,须设置区域III。
4.3 环向盲管间距
假定区域Ⅲ厚度为6 m;围岩与其渗透系数比值为40;区域Ⅱ厚度为0.8 m;围岩与其渗透系数比值为800。计算环向盲管及土工布设置参数与涌水量的关系,绘制曲线如图8所示。
图8显示,随环向盲管间距的增加,渗流稳定时隧道涌水量逐渐下降,且敏感性不断增强。固定环向盲管间距,隧道涌水量随土工布厚度的增加而逐渐增加,但敏感性逐渐下降。
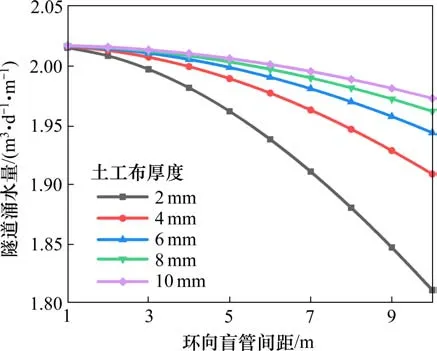
图8 环向盲管及土工布设置参数与涌水量的关系Fig.8 Relationship between setting parameters of circumferential blind pipe and geotextile with water inflow
计算环向盲管及土工布设置参数与支护结构承担水头的关系,绘制曲线如图9所示。
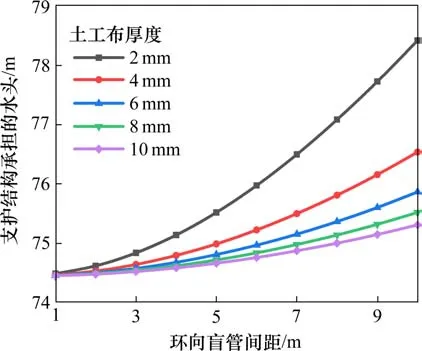
图9 环向盲管及土工布设置参数对支护结构承担水头的影响Fig.9 Influence of setting parameters of circumferential blind pipe and geotextile on water head borne by supporting structure
图9显示,随环向盲管间距的增加,渗流稳定时支护结构承担的水头逐渐增加,且敏感性不断增强。固定环向盲管间距,支护结构承担的水头随土工布厚度的增加而逐渐减弱,但敏感性逐渐下降。
图8和图9显示,环向盲管间距及土工布厚度对隧道涌水量及支护结构承担的水头均有重要影响。究其原因,环向盲管间距减小及土工布厚度增大均会加强隧道三维排水体系,导致排水作用增强,进而影响隧道涌水量及各结构承担的水头。
5 结论
1) 构建了考虑支护结构内缘承担水头的深埋隧道涌水简化计算模型,推导了涌水量及结构外缘承担水头的计算式,其计算结果可退化到忽略支护结构内缘承担水头时的计算表达式。
2) 富水区隧道结构设计时应先对支护结构进行计算,当仅设计支护结构无法同时满足受力及涌水时须考虑注浆加固结构。
3) 适当提高注浆圈的抗渗性能可有效降低隧道涌水量,注浆设计时须对注浆圈厚度及渗透系数进行合理取值。
4) 通过算例分析,考虑支护结构内缘承担的水头时,隧道涌水量预测误差可由9.8%降低为6.1%,一定程度提高了隧道涌水量预测精度。

