风积沙-土工格栅界面摩擦特性拉拔试验研究
聂如松,谭永长,郭一鹏,马世平,施文龙
(1.中南大学 土木工程学院,湖南 长沙 410075;2.长沙理工大学 土木工程学院,湖南 长沙 410114;3.新疆和若铁路有限责任公司,新疆 且末 841900)
新疆新建和若铁路途径塔克拉玛干沙漠南缘,沙漠地区路基优质填料匮乏,但铁路沿线广泛分布风积沙。采用风积沙作为路基填料时,已有不少学者对风积沙的物理力学性质展开过研究。风积沙具有颗粒均匀、级配不良、含水率小、无黏聚力、振动难压实等特点,其组成以粉、细砂为主[1−4],根据《铁路路基设计规范》(TB 10001—2016)[5]填料组别的分类,属于C3组填料。土工格栅强度高,施工简便,价格低廉,抗老化性能好[6−7],将其作为加筋材料埋置在风积沙中,可以减小路基不均匀沉降,提高路堤的稳定性。土工格栅与填料间的相互作用是决定加筋效果的关键因素,MCGOWN等[8]认为拉拔试验能够反映土工格栅在填料中工作的真实情况,因此,国内外学者普遍以拉拔试验来研究筋土相互作用。杨广庆等[9]认为土工格栅的拉拔力可以分为3个部分:1) 土工格栅表面与土体的摩擦力;2) 土工格栅横肋与土粒之间的被动阻力;3) 土工格栅网孔内土体与网孔外土体间的摩擦力。徐超等[10]进行了砂土−土工格栅纵、横肋相互作用机制的拉拔试验研究,并指出纵肋与横肋的减少会导致格栅拉伸模量、网格刚度等的降低,从而导致筋土作用机制的改变。NAMJOO等[11]利用双向土工格栅开展不同含水率下的拉拔试验,发现筋土界面内摩擦角随含水率的增大而减小。杨和平等[12]研究了不同膨胀土、上覆压力、含水率和格栅尺寸对筋土界面摩擦特性的影响。张正等[13]运用拉拔试验研究了不同法向应力作用下土工格栅−黄土相互作用机制,结果表明法向应力对土工格栅拉拔阻力有明显的影响。周建等[14]利用平潭标准砂进行了一系列不同法向应力情况的拉拔试验研究,得出界面似摩擦因数与法向应力相关。阎凤翔等[15]研究了格栅−建筑渣土的界面摩阻特性,结果表明界面摩阻强度包络线符合线性关系,似摩阻系数和似黏聚力都与格栅类型有关。WANG等[16]通过FBG和拉拔试验仪分析了土体压实度、初始法向应力和嵌固端固定形式对筋土作用机制的影响。马存明等[17]通过分析格栅表面摩擦力,指出在高围压和高法向应力时,格栅才会被拉断。CARDILE等[18]总结一系列拉拔试验结果,提出了一种确定土工格栅抗拉拔阻力峰值的计算方法。MORACI等[19]提出了一种计算粗粒土中土工格栅拉拔阻力与残余拉拔阻力的方法。万亮等[20]通过开展加筋膨胀土的拉拔试验,分析了筋材的初始张拉状态、温度和界面残余强度等新因素对格栅加筋膨胀土拉拔试验测试值的影响。筋土界面摩擦特性是评价筋土间相互作用的重要指标,国内外学者对筋土界面摩擦特性的研究收获颇丰,但对风积沙−土工格栅界面摩擦特性的相关研究甚少。本文利用拉拔试验仪,开展风积沙-土工格栅拉拔试验研究,分析不同法向应力、不同压实度和不同土工格栅对筋土界面摩擦特性的影响,研究结果可为风积沙加筋路堤的设计和施工提供一定的参考。
1 试验方案设计
1.1 试验材料
试验所用材料为风积沙和2种双向土工格栅。风积沙来自于和若铁路施工现场,图1为试验所用风积沙,对试验使用风积沙开展基本物理性质试验,试验结果见表1,颗粒级配曲线见图2所示,可见其粒径主要分布在0.075~0.25 mm,颗粒分布均匀,级配不良。试验所用2种土工格栅均为聚丙烯双向土工格栅,如图3所示,将其分别编号为1号土工格栅和2号土工格栅,其基本技术指标见表2。
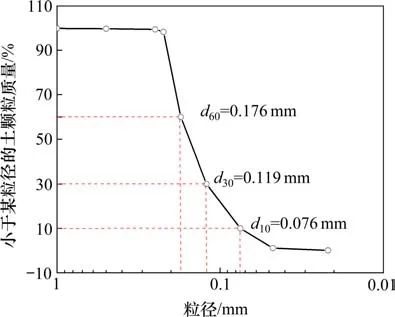
图2 风积沙颗粒级配曲线Fig.2 Grain size distribution of aeolian sand

图3 双向土工格栅Fig.3 Biaxial geogrids

表1 风积沙基本物理力学性质Table 1 Physical and mechanical properties of aeolian sand

表2 土工格栅基本技术指标Table 2 Basic specifications of geogrids
1.2 试验仪器
试验采用仪器为YT1200S型拉拔试验仪,见图4,仪器由数据采集系统、水平拉拔力加载系统、法向应力加载系统、试验箱和夹具等组成,拉拔试验箱尺寸为250 mm×200 mm×200 mm(长×宽×高),位移传感器精度为0.001 mm,位移行程为200 mm,拉拔力精度为±0.02%,伺服荷载法向力范围为0~400 kPa,伺服调速范围为0.1~100 mm/min。

图4 拉拔试验仪Fig.4 Pullout test apparatus
1.3 试验设计
本试验考虑法向应力、压实度对筋土界面摩擦特性的影响。考虑到土工格栅埋置在路基不同深度位置处,法向应力σn取15,30,60和90 kPa。风积沙填料压实度取K=0.90,0.93,0.95。本次拉拔试验全部采用应变控制方式,拉拔速率为0.5 mm/min,本次拉拔试验以格栅拉拔端的位移为15 mm时或当格栅被拉断时作为试验的破坏标准,且每种工况重复5次试验,拉拔试验方案见表3。

表3 拉拔试验方案Table 4 Strength index of the frictional resistance of interface between aeolian sand and geogrids
受试验箱尺寸大小的限制,需要确定格栅的合理宽度,来减小试验过程中试验箱侧壁和风积沙之间的摩擦对拉拔试验结果的影响。杨广庆[23]认为土工格栅宽度约为试验箱宽度的3/4时能够最小化侧壁摩擦效应,因此,试验中土工格栅的宽度为150 mm,试验过程中,侧壁涂抹凡士林进一步减小侧壁的摩擦效应。
拉拔试验具体步骤如下:1) 试验前按3%的含水率配置风积沙试样,放在封闭容器中润湿24 h,使风积沙试样含水率均匀;按长280 mm×宽150 mm尺寸裁剪土工格栅,使不同土工格栅试样在宽度和长度上具有较好的一致性和对称性;2) 将试验箱分4层填筑压实,每层填土50 mm;3)当第2层风积沙(高度为100 mm)填筑压实找平后,铺设土工格栅。土工格栅在试验箱中的长度为250 mm,拉拔出口位置预留30 mm用于夹具的安装,土工格栅距试验箱两边侧壁各25 mm。4) 在拉拔出口处涂抹凡士林,以免拉拔时卡口摩擦影响试验结果;5) 然后继续分层填筑风积沙,压实至与试验箱顶面齐平,此时填土高度为200 mm;6) 使用夹具夹紧土工格栅,并使夹具离拉拔出口尽可能近,以消除夹具与试验箱之间的格栅变形对试验结果的影响;7) 将刚性加压板平放在填筑好风积沙的顶面,施加设定法向应力,并静止15 min,使风积沙-土工格栅紧密接触;8) 施加水平拉拔力,记录拉拔位移和拉拔力等,直至达到破坏标准。9) 改变法向应力,重复步骤1~8进行试验。
2 试验结果及分析
2.1 风积沙−土工格栅界面摩擦特性影响因素
图5为1号土工格栅在法向应力σn=60 kPa,压实度K=0.95时的多次重复试验结果,由图5可知,随着拉拔位移的增大,界面剪应力不断增大,多次重复试验结果的误差在可接受的范围,表明试验结果较为可靠。为了更好地进行分析,采取5次重复试验所得的界面剪应力平均值作为一个工况下的界面剪应力。

图5 1号土工格栅重复拉拔试验结果Fig.5 Repeated pullout test results of No.1 geogrids
2.1.1 法向应力的影响
图6所示为2号土工格栅在不同法向应力情况下界面剪应力与拉拔位移关系曲线。从图中可以看出,剪应力−拉拔位移关系曲线呈现明显的非线性。剪应力的变化随着拉拔位移的增长大致可以分为3个阶段:1) 在拉拔初期,剪应力随拉拔位移近似线性增长;2) 随着拉拔位移的增加,剪应力的增长速率逐渐变缓;3) 对于应变软化型曲线,随着拉拔位移的继续增加,剪应力达到峰值后略有下降,随后趋于平稳;对于应变硬化型曲线,随着拉拔位移的增加,剪应力不断增加,直至达到破坏标准。
剪应力−拉拔位移曲线呈现应变软化型或者应变硬化型特征与试样压实度和法向应力的大小密切相关。
由图6可知,法向应力对界面剪应力影响显著,在同一压实度的情况下,法向应力越大,剪应力也越大。在压实度K=0.90时,剪应力−拉拔位移关系曲线均为软化型,可能是由于压实度较低,风积沙颗粒接触不密实,剪应力达到峰值后,格栅在填料内部形成整体滑动,从而造成了软化现象。如图6(c)所示,填料压实度K=0.93和0.95时,曲线在法向应力σn=60,90 kPa时表现出硬化的特征,其原因可能是压实度较高,风积沙颗粒间接触较为密实,在法向应力高时,拉拔过程中格栅与风积沙界面发生明显的剪胀作用,从而导致界面上产生附加法向应力,从而使得剪应力持续增大。同时,同一压实度下,随着法向应力的增加,剪应力达到峰值所需的拉拔位移越大。
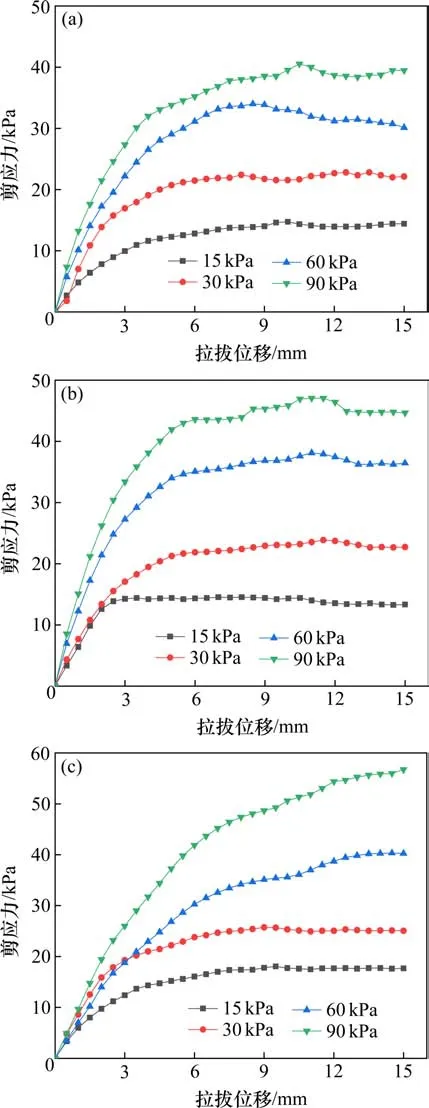
图6 不同法向应力下剪应力−拉拔位移关系曲线Fig.6 Curves of shear stress-pullout displacement under various normal stresses
2.1.2 压实度的影响
图7为法向应力σn=30 kPa时,1号土工格栅在不同压实度下剪应力-拉拔位移关系曲线。由图7可见,在拉拔试验初期,拉拔位移约2 mm前,不同压实度下的界面剪应力相差不大,这是由于试验初期,格栅逐渐被拉紧,筋土未发生相对滑动,拉拔力主要由格栅表面与风积沙填料的静摩擦提供。随着拉拔位移的进一步增加,填料压实度越大,界面剪应力也越大。不同压实度下风积沙颗粒间的紧密程度不同,随着拉拔位移的增加,筋土间产生相对滑移,对于压实度大的填料,格栅网孔内土颗粒咬合更紧,同时土颗粒对格栅横肋的嵌固作用更加显著[9,21],从而造成压实度大时,界面剪应力也变大。

图7 不同压实度下剪应力−拉拔位移关系曲线Fig.7 Curves of shear stress-pullout displacement under various compactness
2.1.3 不同格栅的影响
不同格栅对剪应力−拉拔位移关系曲线的影响比较复杂,其影响因素主要有格栅网孔特征、拉伸强度、纵横肋尺寸等。从图8可以直观地看出,在拉拔试验开始初期,拉拔位移较小,2种土工格栅的界面剪应力差别不大。拉拔位移继续增大,同一压实度下,1号土工格栅的界面剪应力显著大于2号土工格栅。随着压实度从0.90增加至0.95,1号土工格栅界面剪应力峰值增加约48%,而2号土工格栅界面剪应力峰值增加约13%。这些表明1号土工格栅的界面摩擦特性要优于2号土工格栅的界面摩擦特性。产生上述现象的原因可能是,由于拉拔力大部分由横肋产生的被动阻力来分担[19],同时由表2可以看到,1号土工格栅横肋厚度约为2号土工格栅的2倍,这使得1号土工格栅的横肋刚度大于2号土工格栅,在拉拔力相同时筋土间相对滑动就小,这使得2种土工格栅与风积沙填料发生相同相对滑动位移时,1号土工格栅横肋产生的被动阻力更大,因此,1号土工格栅所需拉拔力更大,从而造成1号土工格栅界面摩擦特性要优于2号土工格栅。所以,在进行风积沙路基设计和施工时,应选用横肋力学性能较好的土工格栅。。
2.2 风积沙−土工格栅界面摩擦特性
2.2.1 界面摩擦强度指标
在进行风积沙加筋土路基设计时,土工格栅与风积沙的界面摩擦特性对路基的安全稳定有重要的影响。取破坏标准内最大剪应力为界面抗剪强度τf,得到不同工况下风积沙−土工格栅界面摩擦强度,如图9所示,可见法向应力越大,其界面抗剪强度也越大,界面摩擦强度包线符合公式(1),与土的莫尔−库伦强度准则相似。式(1)中,τf为界面抗剪强度,kPa;σn为法向应力,kPa;f*为似摩擦因数,其中f*=tanφsg,φsg为风积沙−土工格栅界面内摩擦角,(°);csg为表观黏聚力,kPa。通过拟合得到的界面摩擦强度指标见表4所示。

图9 风积沙−土工格栅界面摩擦强度包络Fig.9 Strength envelope of the frictional resistance of interface between aeolian sand and geogrids

由表4可知,随着压实度由0.90提高至0.95,1号与2号土工格栅的似摩擦因数f*和界面内摩擦角φsg不断增大,1号土工格栅在压实度K=0.93和0.95时的似摩擦因数比K=0.90时分别提高约28%和75%,2号土工格栅在压实度K=0.93和0.95时的似摩擦因数比K=0.90时分别提高约26%和50%。在压实度0.90~0.95范围内,2种土工格栅的界面内摩擦角约为17.74°~29.24°;表观黏聚力随压实度的变化不大,在压实度0.90~0.95范围内,2种土工格栅的表观黏聚力约为9.22~12.36 kPa,1号、2号土工格栅的平均表观黏聚力分别为11.36 kPa和10.18 kPa。因此,压实度对筋土界面似摩擦因数的影响要大于对表观黏聚力的影响。风积沙的黏聚力基本为0,而由图8可以看出,在法向应力为0的情况下,筋土界面仍存在一定大小的表观黏聚力,这是由于埋置在风积沙填料中的土工格栅,与其周围填料形成了一个“复合层”,土工格栅的纵横肋限制土体移动,在拉拔时风积沙颗粒形成堆积,并互相咬合而导致的。

图8 1号、2号土工格栅剪应力−拉拔位移关系曲线Fig.8 Curves of shear stress-pullout displacement of No.1 and No.2 geogrids

表4 风积沙−格栅界面摩擦强度指标Table 4 Strength index of the frictional resistance of interface between aeolian sand and geogrids
2.2.2 拉拔摩擦因数
不同于似摩擦因数,拉拔摩擦因数f*R是一个表征风积沙−土工格栅界面摩擦特性的综合参数[22],其定义为界面抗剪强度τf与其对应法向应力σn的比值,如式(2)所示。

图10为1号与2号土工格栅拉拔摩擦因数随法向应力的变化曲线。由图10可知,2种土工格栅在3种压实度下的拉拔摩擦因数随法向应力的关系曲线变化趋势一致,相同法向应力条件下,拉拔摩擦因数随压实度的增加而增大;在相同的压实度条件下,随法向应力σn的增大,拉拔摩擦因数呈非线性减小,其关系曲线可由幂函数进行拟合,如式(3)所示,式中:f*R为拉拔摩擦因数;σn为法向应力,kPa;a和b均为拟合参数。拟合曲线如图10中实线所示,参数拟合结果见表5,由表5可见,拟合程度较好。

图10 拉拔摩擦系数与法向应力的关系Fig.10 Relationship between pullout friction coefficients and normal stress

对比表4与表5中的参数可知,拟合参数a随表观黏聚力的增加而增加,参数b的值随着似摩擦因数的增加逐渐减小。图11为拟合参数a和b分别随表观黏聚力和似摩擦因数的关系,其关系可近似由式(4)和式(5)拟合,式中a1,a2,b1和b2均为拟合参数,参数拟合结果见表6所示,拟合结果良好。将式(4)和式(5)代入式(3)中,可以得到式(6),由式(6)可知,拉拔摩擦因数综合反映了风积沙-土工格栅界面摩擦特性。

表5 拟合参数统计Table 5 Summary of fitting parameters

表6 参数拟合值Table 6 Summary of fitting parameters
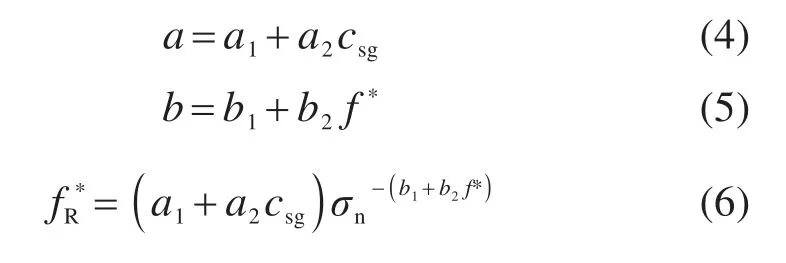

图11 a-csg和b-f*关系Fig.11 Relationship between a-csgand b-f*
2.2.3 界面摩擦因数比
为了分析风积沙−土工格栅界面强度参数的性质,界面摩擦因数比fgs是一个分析风积沙−土工格栅界面强度参数的重要指标,可由式(7)求得。式中,fgs为界面摩擦因数比;φsg为风积沙−土工格栅界面内摩擦角,(°);φss为风积沙的内摩擦角,(°)。

图12为2种土工格栅界面摩擦因数比fgs与压实度K的关系。1号和2号土工格栅的界面摩擦因数比随着压实度K的增加而增加。1号土工格栅界面摩擦因数比在压实度为0.95和0.93时比压实度0.90时分别提高15%和55%,2号土工格栅界面摩擦因数比在压实度为0.95和0.93时比压实度0.90时分别提高12%和33%,这说明压实度对界面摩擦因数比有显著的影响,填料压实度越高,土工格栅的的加筋效果越好。因此,在将土工格栅埋置在风积沙填料中作为加筋材料时,应保证填料有较高的压实度来保证土工格栅作用的发挥。

图12 压实度与界面摩擦因数比关系Fig.12 Relationship between compactness and friction coefficient ratio of the interface
3 结论
1) 剪应力−拉拔位移关系曲线呈3阶段的发展特征,在低法向应力(σn=15,30 kPa)时为软化型,在高法向应力(σn=60,90 kPa)时为硬化型。界面剪应力随法向应力和压实度的增加而增大。同一压实度下,1号土工格栅的界面剪应力显著大于2号土工格栅,1号土工格栅的界面摩擦特性要优于2号土工格栅。
2) 界面摩擦强度与法向应力呈线性关系。似摩擦因数和界面内摩擦角随压实度的提高而增大,表观黏聚力随压实度的变化不大,在压实度0.90~0.95范围内,2种土工格栅的界面内摩擦角在17.74°~29.24°之间,表观黏聚力在9.22~12.36 kPa之间。
3) 相同法向应力条件下,拉拔摩擦因数随风积沙压实度的增加而增大。在相同的压实度条件下,拉拔摩擦因数随法向应力的增加而减小,压实度为0.95时,与法向应力15 kPa时相比,法向应力为30,60和90 kPa时1号土工格栅拉拔摩擦因数分别减少16%,31%和44%,2号土工格栅拉拔摩擦因数分别减少20%,37%和41%。拉拔摩擦因数−法向应力关系曲线可由幂函数进行拟合,拟合参数a与表观黏聚力呈近似线性正相关,似摩擦因数与参数b呈近似线性负相关。
4) 1号和2号土工格栅的界面摩擦因数比随着压实度K的增加而增加。在填料压实度为0.95时,1号、2号土工格栅界面摩擦因数比要比压实度为0.90时分别提高约55%和33%。填料压实度越高,土工格栅的加筋效果越好。

