12号道岔区敷设钢弹簧浮置板的安全性研究

郭无极，曾志平, ，王卫东, ，胡广辉，曾强

(1.中南大学 土木工程学院，湖南 长沙 410075；2.中南大学 重载铁路工程结构教育部重点实验室，湖南 长沙 410075)

随着城市轨道交通的迅猛发展，线路的设计速度逐步提高，较高的运行速度势必带来更大的环境振动。为减少列车对线路周边环境的影响，钢弹簧浮置板等减振措施已广泛应用于城市中振动噪声敏感地段。道岔区是轨道结构的薄弱环节，将钢弹簧浮置板应用于高速道岔区存在着理论检算匮乏的问题。ZHAI等[1−2]应用不平顺激扰模型研究了磨耗程度、行驶速度对列车通过12号道岔轮轨力及车体加速度的影响；为更为真实地反映道岔区真实的轮轨接触关系，KASSA等[3−6]分别给出了道岔区轮轨两点、多点接触的确定方法，并对比实验验证了其正确性。XU等[7−8]基于多点接触轮轨关系的车轨耦合动力学探究了岔区内尖轨、基本轨等的磨耗。XIN等[9]通过LS-DYNA建立了单轮对通过道岔的有限元动力模型，旨在分析道岔的疲劳寿命。多点接触轮轨关系在精确分析岔区各段钢轨受力及磨耗具有更好的精确性，而在轮轨力的计算方面其与不平顺激扰模型具有较好的一致性[10]。且上述研究多针对精确描述轮轨接触点，对下部结构的响应分析较少。本文分别对敷设混凝土整体道床板及敷设钢弹簧浮置板的12号可动心高速道岔进行建模，运用ZHAI[11]提出的车辆-轨道耦合动力学理论及其仿真技术分别计算了列车以时速160 km/h直向逆向、时速50 km/h侧向逆向通过道岔的工况，并对轨道形位变化、行车安全性和舒适性进行了分析。根据中国铁路相关标准进行评估分析，针对浮置板侧倾及部分区域位移超标的情况，提出了隔振器布置的优化方案，论证了列车高速通过敷设钢弹簧浮置板的12号道岔的可行性，为道岔区敷设钢弹簧浮置板提供了理论支撑，为后续钢弹簧浮置板的结构设计及参数优化提供了基础。

1 车辆-轨道-下部结构耦合动力学模型

本文采用ZHAI[11]提出的车辆-轨道耦合动力学理论进行建模，将车辆视为由1个车体、2个构架及4个轮对共7个刚体构成的多体动力学系统，车体与构架之间的二系弹簧及连接轮对与构架的一系弹簧均视为弹簧阻尼器。因为要考虑下部结构响应，本文采用行车激励的方式进行模拟，则每个刚体具有6个自由度，即纵向、横移、沉浮、点头、摇头和侧滚，共计42个自由度。车辆采用地铁A型车参数进行建模。

钢轨模型选用离散支撑的欧拉梁进行模拟，通过轮轨接触模型与车辆模型进行耦合，应用模态叠加法求解在轮轨力作用下钢轨的位移、速度和加速度。将扣件视为弹簧阻尼系统，通过钢轨位移、速度及扣件刚度和阻尼求解扣件力，所得扣件力作为求解下部结构的源项。钢轨及扣件主要参数如表1所示，表1中扣件垂向刚度为扣件垂向静刚度，实际动力学计算采用静刚度的1.4倍。

表1 轨道模型参数Table 1 Parameters of rail

浮置板及基底采用实体单元进行建模。钢弹簧视为弹簧阻尼器连接浮置板与基底。浮置板与浮置板间的剪力较视为刚性梁单元。通过在ANSYS软件搭建几何模型并进行网格划分，输出质量及刚度矩阵。阻尼矩阵的计算采用比例阻尼法，通过关注频段的阻尼比求得阻尼系数，将质量矩阵、刚度矩阵与相应的阻尼系数相乘并叠加求得。将所得矩阵输入耦合动力学求解程序，扣件力作为系统输入，通过Newmark-β法进行迭代求解。建模涉及主要参数如表2和表3所示。

表2 钢弹簧参数Table 2 Parameters of steel springs

表3 下部结构参数Table 3 Parameters of substructure

道岔区钢弹簧浮置板模型俯视图及隔振器布置方式如图1。常规钢弹簧布置方式如图1(b)所示，改良隔振器布置方式如图1(c)所示。因列车通过导曲线及辙岔区域时，列车荷载仅作用于浮置板一侧，在偏载作用下浮置板会发生侧倾，为减小浮置板的侧倾角，改良布置方案在常规布置方案的基础上，将浮置板两侧隔振器外移了200 mm，将部分布置于板中的隔振器移至板边。因列车通过转辙区域及辙岔区域时存在较大的轮轨冲击，改良布置方案在常规布置方案的基础上，于尖轨及心轨位置增设了钢弹簧。

图1 下部结构模型Fig.1 Model of substructure

众多学者对道岔区不平顺的模拟提供了多种方式，转辙区尖轨及可动心轨不平顺可以通过余弦函数进行描述[1−2,12−14]，固定辙岔区不平顺可采用前正弦波后三角形的规范曲线进行描述[2,15−16]，近年来随着计算技术的飞跃发展，道岔区不平顺也开始通过钢轨廓形变化进行描述，运用轮轨多点接触模型进行模拟[3−8,17−19]。综合考虑计算精度与计算效率，本文采用余弦函数对可动心道岔的尖轨与心轨处的不平顺激励进行描述。

因所用三维轮轨接触模型为非线性模型，其求解时间步长不宜超过0.000 1 s，而模型整体尺寸较大、实体单元自由度众多，采用过小的计算步长将导致计算时间过长。故选用异步长分别求解车轨结构及轨下实体结构。在满足收敛条件情况下，空间积分步长由行驶速度确定。

因下部结构为钢弹簧浮置板地段刚度较整体道床板偏低，列车直向或侧向通过道岔板时，车辆载荷集中总用于浮置板一侧，在偏载作用下浮置板会发生侧倾，因此在车辆动力学方程进行了细化，在文献[11, 20−21]车辆动力学模型中车辆各部分横向、沉浮和侧滚平衡方程中引入了道床板侧倾角，以车体为例，新方程如下所示：

式(1)为车体横移运动方程，式(2)为车体沉浮运动方程，式(3)为车体侧滚运动方程。其中：M为车体质量；Y和Z为车体位移；V为车辆运行速度；R为车体质心与轮轨接触点垂向距离；r为车体质心的绕x轴的旋转半径；θ为外轨超高角；ω为道床板侧倾角；Fyt为二系悬挂作用于车体y方向合力；Fzt-为二系悬挂作用于车体z方向合力；a为车体质心与轮轨接触点横向距离；Ix为车体绕x轴的转动惯量；ϕ为车体侧滚角；Mx为绕x轴旋转的合力矩。同理，轮对及构架的运动方程在变换中仅将原有外轨超高角θ替换为外轨超高角θ与道床板侧倾角ω之和，在此不做展示。道床板侧倾角ω与外轨超高角θ不同，前者是一个随时间及位置动态变化的量，后者是一个随位置变化而与时间无关的量。在计算中车辆不同结构质心位置的道床板侧倾角ω通过提取上一时间步道床板有限元模型左右两侧位移，计算出道床板的不同节点位置的侧倾角，再通过插值得到。

图2为行车速度50 km/h下，轴重13 t列车直向逆向通过12号道岔的轮轨垂向力时程曲线，通过本文所述模型与文献[17]中计算结果的对比，可验证所建模型的可行性。

图2 数值仿真的结果比较Fig.2 Comparison of the results of numerical simulation

2 轨道结构变形分析

图3和图4分别展示了敷设常规钢弹簧敷设地段及敷设改良后地段的轨道结构变形。由图3可知，列车逆向侧向通过常规钢弹簧浮置板地段左右侧浮置板垂向位移最大值为3.14 mm和3.21 mm，曲基本轨及曲尖轨垂向位移最大值为3.63 mm和3.69 mm；列车逆向直向通过常规钢弹簧浮置板地段左右侧浮置板垂向位移最大值为3.23 mm和3.06 mm，直基本轨及直尖轨垂向位移最大值为3.73 mm和3.62 mm。

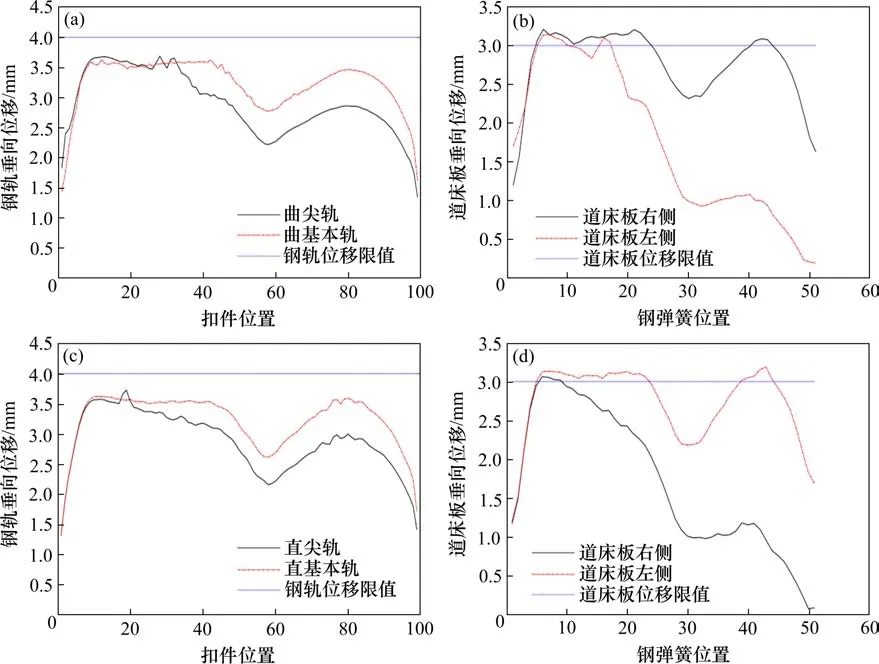
图3 常规钢弹簧浮置板地段轨道结构变形Fig.3 Deformation of conventional floating plate track structure

由图4可知，列车逆向侧向通过改良钢弹簧浮置板地段左右侧浮置板垂向位移最大值为2.92 mm和2.98 mm，曲基本轨及曲尖轨垂向位移最大值为3.40 mm和3.47 mm；列车逆向直向通过改良钢弹簧浮置板地段左右侧浮置板垂向位移最大值为2.93 mm和2.85 mm，直基本轨及直尖轨垂向位移最大值为3.50 mm和3.40 mm。

图4 改良钢弹簧浮置板地段轨道结构变形Fig.4 Modified floating plate track structure deformation

参照中国现行标准[22−23]，敷设常规钢弹簧浮置板地段，钢轨位移均小于4 mm限值；在4~24号钢弹簧位置区间内，存在浮置板位移超过3 mm限值的情况；敷设改良钢弹簧浮置板地段，钢轨位移均小于4 mm限值；浮置板位移均小于3 mm限值。改良浮置板的隔振器布置方式有效改善了浮置板位移超标的现象。

相较常规钢弹簧浮置板地段，改良钢弹簧浮置板地段浮置板的侧倾现象有所好转，内外轨垂向位移差异有所降低。通过在尖轨及心轨位置呢增设隔振器，也有效控制了浮置板在转辙区、导曲线和辙岔区部分浮置板位移超限的问题。

3 行车安全性及舒适性分析

对轴重17 t的地铁A型车分别以时速160 km/h逆向直向、50 km/h逆向侧向通过敷设混凝土整体道床板及敷设改良钢弹簧浮置板的12号可动心高速道岔工况的计算进行分析。

图5为车辆以50 km/h的速度逆向侧向通过敷设改良钢弹簧浮置板道岔区段及敷设混凝土整体道床板道岔区的轮轨垂向力。由图5可知，在转辙区域及心轨区域，轮轨冲击力较大；在车辆驶过尖轨尖端进入导曲线后，呈现出明显的曲尖轨增载、曲基本轨减载的现象，这是由于车辆以时速50 km/h通过曲线时，存在84 mm欠超高。改良浮置板道床地段转辙区最大垂向轮轨力150.33 kN，辙岔区最大垂向轮轨力222.89 kN，混凝土整体道床板地段转辙区最大垂向轮轨力150.03 kN，辙岔区最大垂向轮轨力218.14 kN。

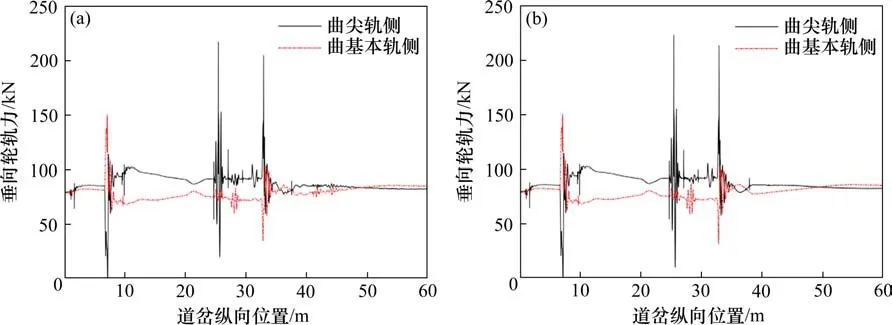
图5 逆向侧向过岔垂向轮轨力时程曲线Fig.5 Vertical wheel track force of lateral crossing turnout

图6为车辆以160 km/h的速度逆向直向通过敷设改良钢弹簧浮置板道道岔区段及敷设混凝土整体道床板道岔区的轮轨垂向力。由图6可知，在转辙器区域及心轨区域，轮轨冲击力较大。改良浮置板道床地段转辙区最大垂向轮轨力163.00 kN，辙岔区最大垂向轮轨力222.41 kN，混凝土整体道床板地段转辙区最大垂向轮轨力160.80 kN，辙岔区最大垂向轮轨力219.91 kN。对比可知，车辆在行经钢弹簧浮置板道床时的轮轨力略大于混凝土整体道床板地段，这是由于浮置板振动造成的，但总体而言不存在显著差异。

图6 逆向直向过岔垂向轮轨力时程曲线Fig.6 Vertical wheel track force of straight crossing turnout

在中国的现行轨道车辆验收及检验标准中，除轮轨力外，还会以脱轨系数及轮重减载率作为行车安全性的评判指标。其中脱轨系数以0.8为限值，轮重减载率以0.6为限值(20 Hz滤波后)；车体横向加速度限值为0.6 m/s2，车体垂向加速度限值为1.0 m/s2。行车舒适性评价指标包括车体横向和垂向加速度[24−25]。对比混凝土整体道床板地段与钢弹簧浮置板道床地段的各项指标如表4所示。浮置板道床的各项安全性及平稳性指标均符合规范要求，但略大于混凝土整体道床板地段。

表4 安全性及平稳性指标Table 4 Safety and smoothness indicators

4 结论

1) 在列车通过敷设钢弹簧浮置板的道岔区域时，浮置板最大位移出现在尖轨及心轨位置，与垂向轮轨力最大位置相符。需在该位置加设隔振器、提高下部基础刚度，以保证轨道结构位移均匀。

2) 列车通过敷设钢弹簧浮置板的道岔区域时，直向通过及侧向通过均会造成浮置板两侧位移不均匀、浮置板向行车侧倾斜的情况。通过将隔振器向板边移动，可达到降低浮置板单侧位移，改善浮置板侧倾的效果

3) 在常规钢弹簧浮置板地段，列车逆向侧向通过时左右侧浮置板垂向位移最大值为3.14 mm和3.21 mm，曲基本轨及曲尖轨垂向位移最大值为3.63 mm和3.69 mm；列车逆向直向通过时左右侧浮置板垂向位移最大值为3.23 mm和3.06 mm，直基本轨及直尖轨垂向位移最大值为3.73 mm和3.62 mm。

4) 在改良钢弹簧浮置板地段，列车逆向侧向通过时左右侧浮置板垂向位移最大值为2.92 mm和2.98 mm，曲基本轨及曲尖轨垂向位移最大值为3.40 mm和3.47 mm；列车逆向直向通过时左右侧浮置板垂向位移最大值为2.93 mm和2.85 mm，直基本轨及直尖轨垂向位移最大值为3.50 mm和3.40 mm。

5) 列车逆向侧向通过敷设钢弹簧浮置板道岔区时，轮重减载率为0.73，脱轨系数为0.46；列车逆向直向通过敷设钢弹簧浮置板道岔区时，轮重减载率为0.26，脱轨系数为0.21；在道岔区敷设钢弹簧浮置板道床的各项安全性及平稳性指标均符合规范要求，但略大于混凝土整体道床板地段。