一种GNSS测码伪距绝对定位求解方法*

常占强 ，刘家喜 ，钱淑君 ，张妍欣 ，郑浩鑫

（1.首都师范大学资源环境与旅游学院，北京 100048；2.三维信息获取与应用教育部重点实验室，北京 100048；3.山东省第四地质矿产勘查院，山东 潍坊 261021）

0 引 言

全球卫星导航系统（global navigation satellite system，GNSS）泛指中国的北斗（Beidu）、美国的GPS（globalpositioning system）、俄 罗 斯 的GLONASS（global navigation satellite system）和欧洲的伽利略（Galileo satellite navigation system）.现今，GNSS定位导航功能不仅广泛应用于军事、测绘、公安交通、数字测图、精细农林业及土地资源调查与勘测等领域［1-9］，并已渗透到人类日常生活中，如旅游、野外探险等.其中，GNSS测码伪距绝对定位仅用一台接收机不需要进行差分处理就可实现全球快速定位导航，在军事、公安交通、车辆舰船定位导航、精细农林业、土地资源调查与勘测等领域中发挥着重要作用.尤其是精确单点定位技术（pre‐cise point positioning，PPP）定位精度可达厘米级，受到了越来越广泛的关注［10-21］.当前，GNSS 测码伪距绝对定位坐标解算方法有常规经典算法和求差法2种［22-26］：常规经典法同时接收处理4颗GNSS卫星信号即可实现定位，但需要GNSS接收机初始概略坐标值，再用泰勒级数展开将伪距观测方程线性化；求差法不需GNSS接收机初始概略坐标值，但需多接收处理1颗GNSS卫星信号才能实现定位，在一定程度上限制了GNSS的定位区域，特别是在地形复杂的山区峡谷地带和森林茂密地区等GNSS卫星信号接收困难区.本文将在对2种方法进行系统分析的基础上，提出一种改进的测码伪距绝对定位处理方法，并用实例对其进行验证.

1 GNSS测码伪距绝对定位算法分析

1.1 常规经典算法

GNSS测码伪距定位是依据GNSS卫星坐标和测码伪距为已知量建立观测方程实现的.其测码伪距观测方程可表示为

为实现绝对定位，GNSS接收机需同时接收处理4颗以上GNSS卫星信号，建立4个以上观测方程可解算出4个未知数：GNSS接收机三维坐标（X，Y，Z）及接收机时钟误差δtT.但方程式（1）为非线性方程，一般用泰勒级数展开将其线性化.设GNSS接收机初始概略坐标为（X0，Y0，Z0），将式（1）用泰勒级数展开，略去2次以上项，则

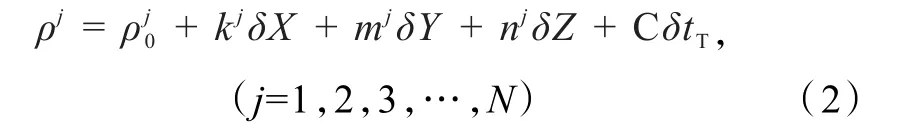
式中：ρj是经过电离层、对流层以及卫星时钟误差改正后的距离，为已知量；ρj0=kj、mj、nj分别是星站欧氏距离在X、Y、Z向的偏导值.

式（2）为线性化后的测码伪距观测方程，可直接求取三维坐标增量（坐标改正数）δX、δY、δZ.若GNSS接收机同时观测处理N颗卫星信号（N＞4），用最小二乘法解出GNSS接收机三维坐标增量，进而解算出GNSS接收机三维坐标

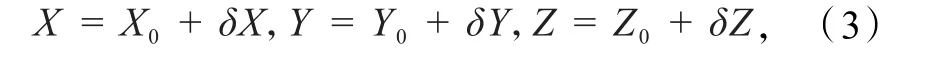
再经过若干次递归迭代，最后得到GNSS接收机精确坐标.如上所述，用泰勒级数展开线性化需预知GNSS 接收机的初始概略坐标值（X0，Y0，Z0）.然而，GNSS接收机初始概略坐标很难预知.鉴于此，通常将其设为（0，0，0）［25-26］.但若所选取接收机初始概略坐标值与精确值偏差较大，则泰勒级数展开略去的2次以上项将对解算结果产生显著影响［25-26］，甚至级数发散导致迭代求解失败.显然，获取接收机初始概略坐标为此方法的关键所在.

1.2 求差法

为了在GNSS接收机初始概略坐标未知情况下获取接收机精确三维坐标值，文献［22-23］提出了求差线性化观测方程法.其主要过程为：

先对式（1）移项，再两边平方得

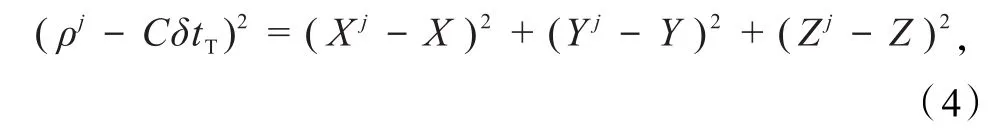
若GNSS接收机同时接收5颗GNSS卫星信号（j=1，2，3，4，5），即建立 5个测码伪距观测方程；再将通式（4）中式j+1两边与式j（j=1，2，3，4）两边相减得到4个线性方程

式中，aj、bj、cj、lj为方程组系数，aj=2(Xj+1-Xj)；bj=

求解式（5）线性方程组可得到GNSS接收机三维精确坐标值（X，Y，Z）.可见，求差法不需预知GNSS接收机的初始概略坐标，通过对伪距观测方程求差处理实现伪距观测方程的线性化，以解出接收机三维坐标.如上所述，此方法需额外增加1颗GNSS卫星信号可求解出接收机的精确三维坐标.这对于在卫星信号接收困难区域，如高楼林立大都市与地形复杂地区（山谷、盆地、树木茂密地带）的定位与导航增加一定难度.

2 对GNSS测码伪距绝对定位求解法的改进

GNSS接收机在卫星信号接收不理想的区域只能接收4颗GNSS卫星信号，且GNSS接收机初始概略坐标未知，无论是常规经典算法和求差法都无法求解GNSS接收机三维精确坐标.本文将提出一种GNSS测码伪距绝对定位处理方法，在不增加GNSS卫星接收个数的情况下，即仅接收4颗GNSS卫星信号，也可解算出GNSS接收机三维精确坐标.

首先与求差法中式（5）类似，GNSS接收机同时接收4颗GNSS卫星信号则可建立4个测码伪距观测方程（j=1，2，3，4），再通过式 j+1两边与式 j两边相减得到以下线性方程

式中：X、Y、Z为GNSS接收机的三维坐标；δtT为接收机时钟误差；aj、bj、cj、lj为方程组系数，将式（6）移项得

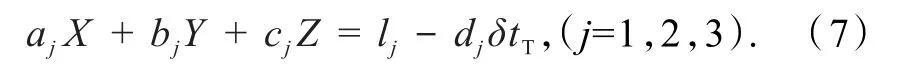
由于接收机时钟稳定性通常为10-10～10-11量级，而时钟误差δtT一般为±10-7s量级，与自由项系数lj相比非常微小，现暂将其忽略，则式（7）可简化为

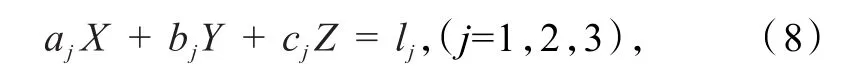
显然，由式（8）可直接解出GNSS接收机的三维坐标.由于此前忽略了微小量δtT，因此如此解出的并非GNSS接收机精确坐标值，但可作为其三维初始概略坐标（X0，Y0，Z0），现将其值代入式（2），可计算出三维坐标增量（坐标改正数）（δX，δY，δZ）；再经过递归迭代，最后获取到GNSS接收机精确坐标值（X，Y，Z）.

3 实验分析与验证

为了验证本文所提出方法的可靠性与精确性，作者用实测数据在GNSS接收机的初始概略坐标值未知的情况下，用4颗GPS卫星信号数据，求取GPS接收机精确三维坐标.

现以三维信息获取与应用教育部重点实验室1台GPS接收机2021年10月20日在GPS历元TOW（time of week）：268008接收的 GPS导航电文数据为例，对本方法进行实验分析验证.从卫星星历中获取的4颗GPS卫星坐标和各颗卫星与接收机间观测伪距以及电离层和对流层延迟差见表1；用本算法求取的GPS接收机概略坐标以及由此迭代计算出的精确坐标如表2所示.由此可见，在无GPS接收机初始概略坐标情况下，本处理方法仅用4颗GPS卫星信号数据，计算出了GPS接收机精确三维坐标.

表1 4颗卫星的GPS卫星坐标和主要参数 单位：m

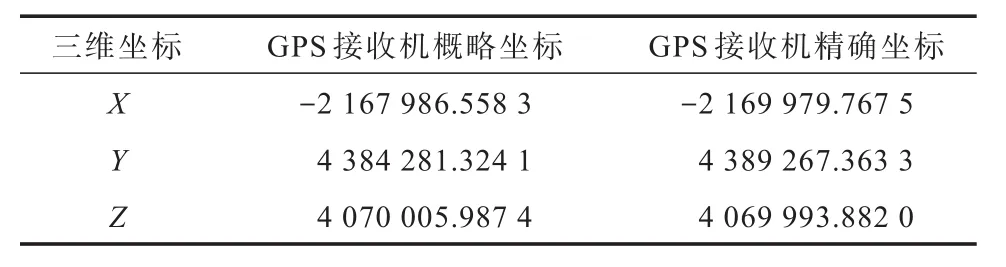
表2 用实际数据计算出的GPS接收机概略坐标与精确坐标 单位：m

在计算环境为Intel（R）Core™i7-2600，CPU为3.4G下，对本方法与常规经典法的工作性能进行了对比，二者都是用4颗卫星信号数据，在用常规经典算法计算中，按照通常做法将初始概略坐标设为（0，0，0）［24-25］，本文所提出的处理方法计算迭代次数为4，明显少于常规经典方法的6次，且消耗时间也较短仅为81 ms，而常规经典方法的消耗时间为124 ms.这说明由于求取了GPS接收机概略坐标值而加速了级数收敛，对于减少迭代次数发挥了关键作用，并使得实际计算消耗时间较经典方法显著缩短.此外，需要指出的是，若所选取的初始概略坐标值偏差较大，即三维坐标改正数 δX，δY，δZ 较 大 .此时常规经典方法用泰勒级数展开线性化测码伪距观测方程时，其2次以上级数余项不再是“微小项”，很可能因为级数发散而导致迭代求解失败；而对于本文所提出的方法，则不存在此问题，因此具有较高的鲁棒性.

4 结 论

现有GNSS测码伪距绝对定位的2种解算方法各具特色：常规经典算法需预知GNSS接收机的初始概略坐标；求差法不需预知GNSS接收机初始概略坐标但需GNSS接收机多接收处理1颗GNSS卫星信号才能实现定位.本文提出了一种改进的GNSS绝对定位处理方法，此方法兼具经典常规法和求差法的优势.即使在未知GNSS接收机初始概略坐标的情况下，仅接收4颗GNSS卫星信号即可精确求取GNSS接收机的三维坐标值.这对于GNSS卫星信号接收困难区域，如在地形复杂的山区峡谷地带、森林茂密地区以及高楼林立的大都市，实现GNSS绝对定位具有较高的理论意义与应用价值.