基于全局采样集优化的联合多维度平滑性时变图信号重构*

陈熠罡，吴贇

（东华大学，上海 201620）

0 引言

随着图论研究的深入，以图为基础的数据处理逐渐进入各个领域研究人员的视野，进而推动了图信号处理领域的急速发展。图信号处理是近年来受到广泛关注的一个新的研究方向，它主要分析由图捕获的不规则域上的信号[1]，并在传感器网络[2-3]、机器学习[4-5]、推荐系统[6-7]、生物医学[8-9]、图像处理[10-12]等领域中有着优势地位。

现阶段在对图信号的研究过程中，人们主要使用图滤波和图傅里叶变换[1]等方法对单个图信号进行处理，但此时的图信号是静态的图信号，和现实世界中的图信号相比不具备时变性。因此，对时变图信号的研究引发了研究人员的关注。由于采集到的图信号数据往往具有时变特性，在实际应用中，数据缺失或不正确的问题非常普遍。为了解决相关问题，时变图信号重构成为实际应用中的一个重要课题。例如，在低成本的传感器网络中，如空气温度传感器网络，由于传感器故障或通信故障，数据丢失是常见的，此时便需要对时变信号进行重构。

近年来，图信号数据重构是信号处理领域中的热门问题。对时变图信号的研究首次出现在文献[13]中。文献[13]在处理时变图信号的重构问题时提出了两种方法，一种是批量处理重构，另一种是在线分布式重构。两种方法的主要思想是先将收集到的图信号数据按时间顺序排列，再对数据进行采样，并通过采样数据恢复所有信号数据。文献[14]采用差分处理方法使得时变图信号数据具有更好的平滑特性，取得较好的重构效果。文献[15]利用时变图信号在空间域和时间域都具有平滑性的特点，提出了基于联合平滑性的时变图信号重构算法。但以上3种方法对空时域平滑性的挖掘还不够深入，并且采样时均采用随机采样方法，采样节点不具备代表性。

针对以上分析，本文对加权无向图上的时变图信号重构展开研究。和常用的随机采样不同，本文根据节点的区域关联性，对图结构进行分簇，在每个簇内选取具有代表性的节点数据，实现采样集优化。通常情况下，传统的时变图信号重构方法为簇内重构，即对图结构分簇之后，在每个簇内进行重构，但此时忽略了簇与簇之间边的权重，重构结果会有很大的误差。本文采用的重构形式则为全局重构，即在整个图结构上进行重构。同时，本文对时变图信号在空时域的特征进行深入挖掘，提出基于全局采样集优化的联合多维度平滑性时变图信号重构算法（Joint Multidimensional Smoothness Time-Varying Graph Signal Reconstruction Based on Global Sampling Set Optimization，JMSR-GSSO-TVGS）。实验证明，本文的方法能够得到较好的重构质量。

1 图信号相关知识

1.1 图的构成

图G可以定义为一个三元组(v,ε,W)，其中v和ε分别表示图中n个节点和e条边的集合。在连通的无向图中，对于集合v中任意两个不同的节点p和q，与每条边(p,q)∈ε相关联的是一个权重wp,q，它反映了节点p和节点q之间的相关性或相似性，并且wp,q=wq,p。W是权重矩阵，wp,q是W的一个元素，位于矩阵W的第p行，第q列。通常情况下，若边(p,q)属于集合ε，则wp,q>0，否则wp,q=0。时变图信号数据集X是一个大小为n×m的矩阵，表示的是n个节点在m个时刻的总数据，第i行数据为向量X(i,:)，第j列数据为向量X(:,j)。xi,j是位于矩阵X的第i行、第j列的一个元素，表示图G的第i个节点在第j个时刻获取到的信息。

1.2 图拉普拉斯矩阵

图拉普拉斯矩阵在图信号处理领域占据着重要的位置。在一个加权无向的图结构图G中，图拉普拉斯矩阵定义为：

式中：矩阵K是对角矩阵，矩阵K的第i个对角元素是v节点i的度数，因此矩阵K被称为图G的度矩阵。由于时变图信号包含空间域和时间域两方面的信息，所以时变图信号的底层图结构可以看作联合时间顶点图，如图1 所示。图1（a）是信号的空间域拓扑图G，图1（b）是长度为T的时间域循环图，图1（c）是联合时间顶点图J。其中，图1（c）是由图1（a）和图1（b）的笛卡尔乘积生成的图。图1（a）和图1（b）的拉普拉斯矩阵分别用LG，LT表示。

图1 联合时间顶点图的生成

2 JMSR-GSSO-TVGS 算法

在图信号领域中，时变图信号重构是研究的重点。在真实世界中，图信号往往会随着时间的变化而变化，因此在图信号采样过程中经常会出现数据错漏的现象。为了更好地重构时变图信号，本文提出了一种JMSR-GSSO-TVGS 算法。该算法在对信号数据进行优选的基础上，进一步挖掘了时变图信号在空时域的多维平滑性，使时变图信号的重构结果更加精确。

2.1 采样集优化

对图信号数据进行重构之前需要对信号数据进行采样。在以往的工作中通常使用随机采样，随机采样虽然可以获取一定数量的采样数据，但是有很大的弊端。对于大规模的图，由于节点与节点之间的权重不同，图结构往往会划分为几个区域，不同区域的节点数据会有些许差别，如果使用随机采样，很有可能采集到同一个区域上的节点数据，此时采集到的数据就不具有代表性，势必对图信号的重构结果产生影响。鉴于此，有必要对图信号的采样集进行优化处理。

一般情况下，时变图信号的采样可以表示为：

式中：Y∈Rn×m为经过采样的时变图信号；X为原始的时变图信号；矩阵O∈Rn×m为采样算子，在第m个时刻，若节点的数据被采集，则矩阵元素O(n,m)赋值为1，否则为0；○表示哈达玛积。在实际情况下，噪声是不可避免的，因此本文在研究时变图信号重构即通过Y恢复X时，把噪声纳入了考虑范围，并用矩阵代表噪声。

因为节点的区域关联性对空间域采样有很大的帮助，所以本文根据节点的区域关联性对采样集进行优化。本文采用了一种有效的Louvain[16]算法对图结构进行分簇。Louvain算法是一种社区发现算法，算法目标是优化模块度（modularity）。模块度描述了社区内节点的紧密程度，即节点的区域关联性。分簇结束后，每个簇中的节点有一定的区域关联性，节点数据会比较相似，此时在每个簇中按相同的比例采取节点，并把该节点在矩阵O的相应位置赋值为1，获得优化全局采样算子，进而根据式（2）获得优化采样数据。优化采样数据相较于随机采样数据更能代表整个图结构上数据的总体情况。使用优化的采样数据，图信号重构的准确率将大大提升。

2.2 联合多维度平滑性全局重构

时变图信号的平滑性对信号重构有很大的帮助。平滑性越大，恢复出来的数据越接近原始数据。由于时变图信号在空间域和时间域都具有平滑性，并且在空间域和时间域进行差分处理后的时变图信号具有更好的平滑特性，因此本文采用联合多维度平滑性的方法对时变图信号进行全局重构。此方法可以达到很好的重构效果。

在空间域对图信号做差分处理时，差分算子定义为：

此时差分信号为XDh1=(X(:,2)-X(:,1),X(:,3)-X(:,2),…,X(:,m)-X(:,m-1))。在时间域对图信号做差分处理时，差分算子定义为：

此时差分信号为Dh2X=(X(2,:)-X(1,:)T,X(3,:)T-X(2,:)T,…,X(n,:)T-X(n-1,:)T)T，(·)T表示矩阵的转置。

根据时变图信号总变差的定义[15]，在空间域中，时变图信号的总变差可以表示为tr(XTLGX)；在时间域中，时变图信号的总变差可以表示为tr(XLTXT)，tr(·)表示矩阵的迹。每个时刻图结构上相邻节点数据差值的绝对值之和即为该时刻图信号的总变差。将每个时刻图信号的总变差相加，得到的结果即为时变图信号的总变差。总变差越小，表示时变图信号越平滑。基于时变图信号及其差分信号在空间域和时间域中的联合平滑性，本文建立如下的重构模型：

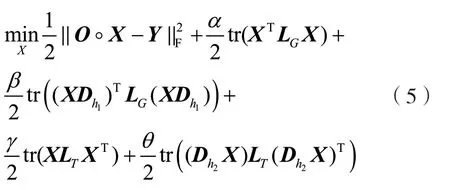
式中：LG为空间域图拉普拉斯矩阵；LT为时间域图拉普拉斯矩阵；α，β，γ，θ>0 均为正则化参数。式（5）中的第2 项表示计算误差，第2 至第4 项表示时变图信号各个维度的总变差，总变差越小，表示恢复的时变图信号越平滑，越符合实际。

为了获得重构信号X，需要对式（5）进行求解。令式（5）为F(X)，此时F(X)为凸优化问题，可以使用迭代算法获得最优解。迭代前需要设置最大迭代次数S，迭代步长τ，以及正则化参数α，β，γ，θ。设置完毕后，使用效果优良的谱共轭梯度法[17]来对F(X)进行迭代求解。

每次迭代都需要使用谱共轭梯度算法。该算法的步骤为：第1 步，确定好每次迭代的步长；第2 步，更新下一步的搜索方向。将第k步的搜索方向表示为∆X k，第k步的最优步长τ由线性最小化规则决定。线性最小化规则为：

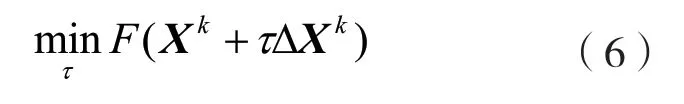
可以通过对式（6）进行求导得到最优迭代步长为：

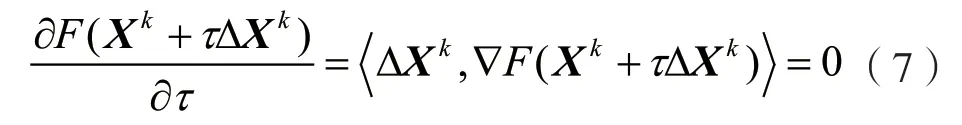
式中：∆F(X)代表F(X)的梯度。∆F(X)的计算方法为：

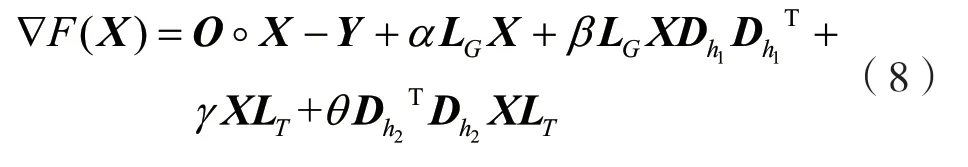
对式（7）进行求解，可以获得迭代步长：

之后可以开始迭代，迭代过程为：

迭代结束后，将第k步的搜索方向和第k+1 步的梯度进行线性组合，从而更新第k+1 步的搜索方向为：

式中：μ为共轭参数；λ为谱参数。

2.3 算法步骤

根据2.1 节和2.2 节所述内容，本文提出的JMSR-GSSO-TVGS 算法的具体步骤归纳如下。

步骤1：获取拉普拉斯矩阵。基于时变图信号联合多维度平滑性的概念，得到空间域图拉普拉斯矩阵LG和时间域图拉普拉斯矩阵LT。

步骤2：获取优化全局采样算子。先对图结构应用Louvain 社区发现算法进行分簇，采样时在每个簇中以一定的采样比例获得每个采样节点的位置，汇总每个簇中的采样节点，获取优化全局采样算子O。

步骤3：采样集优化。根据式（2），使用优化全局采样算子O从总的图信号数据中获得采样数据，实现采样集优化。

步骤4：正则化参数优化。先对参数区间进行网格化，然后在网格化后的参数集合中对正则化参数α，β，γ，θ进行穷举搜索，再使用每一种正则化参数组合通过步骤5～6 进行一次实验测试，选取重构效果最好的一组作为最优参数组合，确定α，β，γ，θ的值。

步骤5：迭代。首先进行初始化设置。迭代次数s初始化为0，设置差分算子Dh1，Dh2，最大迭代次数S，终止迭代阈值ξ。令初始值X0=0，∆X0=-∆F(X0)。迭代步骤如下：

（1）根据式（9）确定迭代步长τ；

（2）根据式（11）更新第k+1 步的搜索方向。

步骤6：迭代终止判断。当k=S或者||∆X k||F≤ξ时，迭代结束，同时获得经过重构后的时变图信号Xk；反之，则k=k+1，并跳转到步骤5 继续迭代重构，直至迭代结束。

若对数据进行随机采样，并采用步骤4～6进行重构，则该重构算法为基于联合多维度平滑性的时变图信号全局重构算法（Joint Multidimensional Smoothness Time-varying Graph Signal Reconstruction，JMSR-TVGS）。

3 实验结果分析

本节使用MATLAB 软件进行仿真实验。实验分别研究分析全球海平面气压数据[18]和室内分布的53 个传感器收集的温度传感器网络数据[19]。全球海平面气压网络拓扑图如图2（a）所示，温度传感器网络如图2（b）所示。在采样过程中，采样率在集合{10%,20%,30%,40%,50%,60%,70%,80%,90%}中选取。一般情况下，最大迭代次数S设置为2×104，终止迭代阈值ξ设置为1×10-6。经过参数区间网格化之后，正则化参数α，β，γ，θ在集合{1 ×10−3,1 × 10−2,2 × 10−2,5 × 10−2,0.1,0.2,0.5,1,2,5,10,20,50,1 × 102,2 × 102,5 × 102}中进行搜索选取。实验均重复50 次。本文使用均方根误差来衡量时变图信号的重构效果，均方根误差越小，重构的时变图信号越接近原始数据。均方根误差定义为：

图2 网络拓扑

式中：X*为重构后的时变图信号；X为原始的时变图信号；Nx为时变图信号的长度。

首先，比较提出的全局采样集优化重构和传统的簇内采样重构的性能。此时簇内重构在每个簇中使用JMSR-TVGS 算法，全局重构使用JMSRGSSO-TVGS 算法。首先使用Louvain 算法将图结构分簇，其次使用JMSR-TVGS 算法对图信号进行簇内重构，最后使用JMSR-GSSO-TVGS 算法对图信号进行全局重构。图3（a）和图3（b）分别展示了对于全球海平面气压数据和温度传感器数据，全局重构与簇内重构结果的误差对比。在图3（a）中，当采样率小于60%时，全局重构信号的误差小于重构后的簇内信号的误差，当采样率等于60%时，两者逐渐接近。在图3（b）中，当采样率小于40%时，全局重构信号的误差小于重构后的簇内信号的误差；当采样率等于40%时，两者的重构效果逐渐相似。由此可见，和簇内重构相比，在低采样率时，使用全局重构的JMSR-GSSO-TVGS，重构性能更为优越。

图3 簇内重构和全局重构实验结果对比

其次，比较本文提出的基于采样集优化的联合多维度平滑性全局重构算法（JMSR-GSSOTVGS）和传统算法的重构性能。对比的重构算法采用随机采样，此类算法有图总变化量重构算法（Graph-regularization）[14]、Tikhonov 正则化重构算法（Graph-time Tikhonov）[14]、基于联合平滑性的重构算法（JSR-TVGS）[15]、批量重构算法（BRTVGS）[13]、联合变差最小化重构算法（JVMR）[15]、基于联合多维度平滑性的全局重构算法（JMSRTVGS）。全球海平面气压数据和温度传感器网络数据的实验仿真结果分别如图4（a）和图4（b）所示。从图4（a）和图4（b）中可以看出：

图4 全局重构实验结果对比

（1）采样率越高，获取的数据信息越多，所提出的算法和其他重构算法的重构误差越低。同时在相同采样率下，对采样集进行优化后，重构的效果更好。例如，在图4（a）中，当采样率为40%时，JMSR-TVGS 和JMSR-GSSO-TVGS 的重构误差分别为0.30，0.28；在图4（b）中，当采样率为30%时，JMSR-TVGS 和JMSR-GSSO-TVGS 的重构误差分别为0.516，0.512。由此可见，本文提出的经过采样集优化的JMSR-GSSO-TVGS 比没经过采样集优化的JMSR-TVGS 重构效果更好。

（2）重构过程中利用的平滑性越多，重构的误差越小。在重构算法中，Graph-regularization 利用了时变图信号空间域平滑性，BR-TVGS 利用了差分时变图信号空间域平滑性，JVMR 利用了时变图信号空间域平滑性和时间域平滑性，JSR-TVGS利用了差分时变图信号空间域平滑性和时变图信号时间域平滑性。本文提出的JMSR-GSSO-TVGS 利用了差分时变图信号的空间域平滑性和时间域平滑性，以及时变图信号的空间域平滑性和时间域平滑性。和这些重构算法相比，JMSR-GSSO-TVGS 更充分地利用了空时二维平滑性，获得了更小的重构误差。例如，在图4（a）中，当采样率为40%时，Graph-regularization、Graph-time Tikhonov、BRTVGS、JVMR、JSR-TVGS 和JMSR-GSSO-TVGS 的重构误差分别为0.42，0.37，0.31，0.37，0.32 和0.28；在图4（b）中，当采样率为30%时，Graphregularization、Graph-time Tikhonov、BR-TVGS、JVMR、JSR-TVGS 和JMSR-GSSO-TVGS 的重构误差分别为0.574，0.562，0.523，0.535，0.519 和0.512。由此可见，JMSR-GSSO-TVGS 可以取得不错的重构效果。

综合两部分的实验结果可知，相较于其他重构算法，本文提出的JMSR-GSSO-TVGS 算法重构性能提升较大。

4 结语

本文研究了位于加权无向图结构上的时变图信号，提出了基于全局采样集优化的联合多维度平滑性重构算法来实现对时变图信号的重构。首先使用基于图结构中节点区域关联性的分簇算法对图结构进行分簇；其次在每个簇中选取规定采样比例的节点数据，实现采样集的优化；最后利用时变图信号的联合多维度平滑性进行全局重构。从实验结果可以看出，基于全局采样集优化的联合多维度平滑性重构算法在采样比例较低时，相较于其他时变图信号重构算法可以取得较好的重构效果，从而证明了本文所提算法对时变图信号重构的可靠性。在后续的工作中，将引入时变图信号的带限性，进一步改进重构性能。