阶跃光激励的光热偏转技术的理论研究*

曾胜财

(厦门海洋职业技术学院 信息工程学院，厦门 361100)

光热偏转技术(Photothermal Deflection Technique, PDT)是一种基于光热效应的非接触式无损检测技术，具有较高的信噪比和空间分辨率、灵敏度高、无需对样品进行预处理等特点, 已在亚表面成像[1-2]、材料的热学参量的测量及研究[3-6]、荧光量子效率测量[7]、速度分布[8]等领域获得广泛的应用.光热偏转技术的基本原理如图1所示，在激励光辐照下，样品表面将吸收光能转换为热能，从而使样品内及相邻媒质的温度升高.因折射率与温度有关，样品及相邻的媒质存在折射率梯度.用一束小功率探测光掠射具有折射率梯度的样品表面时，光束将发生偏转.根据光束偏转角大小，可研究或测量样品的力、热、光学等特性.

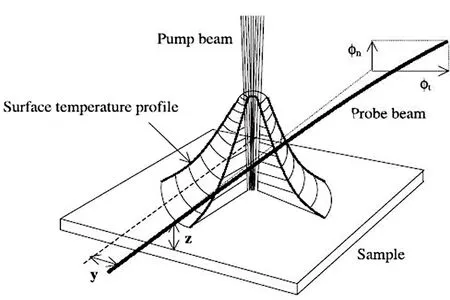
图1 光热偏转技术原理示意图

传统的光热偏转技术需要扫描装置，为获得偏转信号需要用锁相放大器，实验装置较复杂和昂贵，对信号的后续处理也较麻烦和费时，且对时变信号的研究很少.阶跃光激励的光热偏转技术具有实验装置简单、测量速度快、可实时测量等优点，具有较高的应用价值[9-10].Zhou[11]用格林函数法研究阶跃光激励的固体样品的温度分布，但因引入等温和绝热近似简化其理论模型，该模型仅适用于偏转媒质的热扩散率远小于样品热扩散率的情况.本文构建阶跃光激励的光热偏转技术的一维理论模型，基于热传导理论运用拉普拉斯变换求得样品和样品表面空气温度场，以及光热偏转信号的表达式.计算模拟温度梯度和温度场随空间和时间的变化.通过改变探测光离样品表面的距离以及热扩散率的大小，模拟分析光热偏转信号的变化.

1 理论模型

图2为阶跃光激励的光热偏转技术的一维理论模型，偏转媒质为空气，探测光平行样品表面掠射样品附近的空气.根据热传导理论[12]，样品与空气的热传导方程为：

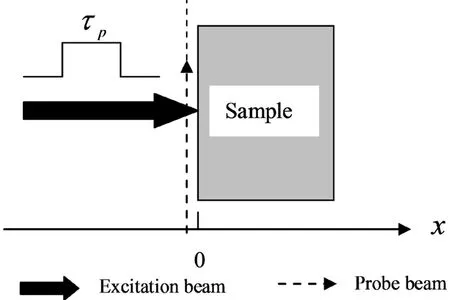
图2 阶跃光激励的一维理论模型

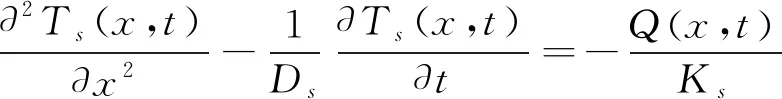
(1)

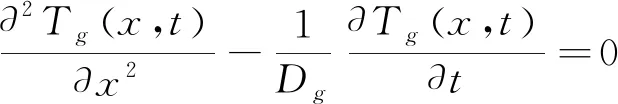
(2)

式中Ts、Tg分别表示样品和空气的温度，Ks是样品的热导率，Ds、Dg分别表示样品和空气的热扩散率，其中热扩散率D=K/ρC，ρ、C分别表示密度和比热.Q(x,t)是样品中的热源功率密度，可表示为：

Q(x,t)=βηI(t)exp(-βx)

(3)

式中β为样品的光吸收系数，η为光能转化为热能的效率，I(t)为阶跃激励光，其光强为：

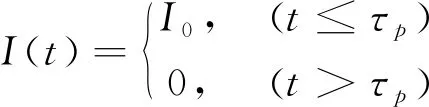
(4)

其中τp为阶跃光的脉宽.阶跃光激励时的边界条件为：

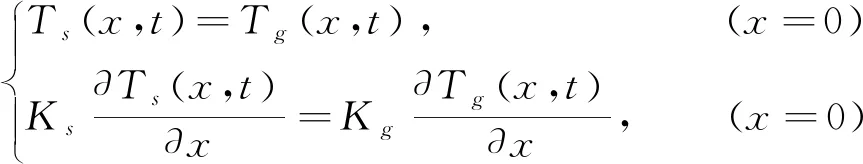
(5)

(6)

初始条件为：

Ts(x,t)=Tg(x,t)=0， (t=0)

(7)

对热传导方程和边界条件进行拉普拉斯变换后得：

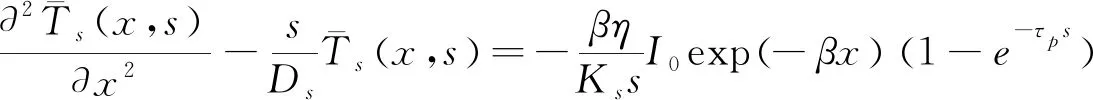
(8)

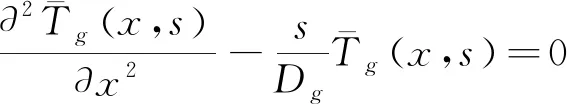
(9)

(10)

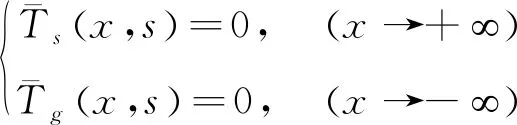
(11)

通过求解上述方程得到样品和空气的温度场分别为：

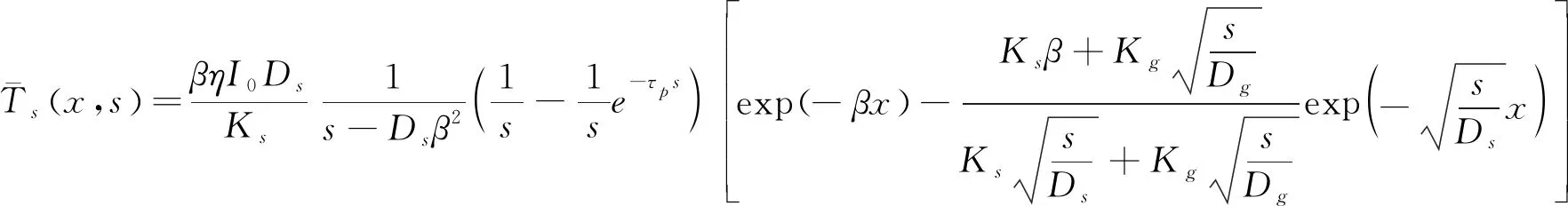
(12)

(13)

根据拉普拉斯变换的卷积定理及查表可得式(12)(13)的逆变换为：

其中式(14a)和式(15a)分别为阶跃光辐照时样品和空气的温度场，式(14b)和式(15b)则为没有光照时的温度场.

在一维情况下，根据光热偏转理论，探测光的偏转角可表示为[13]：

(16)

式中n为偏转媒质的折射率，l为探测光相交处沿探测光方向上激励光的光束宽度，∂n/∂T为偏转媒质的折射率温度系数.将式(15)代入式(16)可得出偏转角表达式：

其中式(17a)为阶跃光辐照时的偏转信号，式(17b)为无光照时的偏转信号.

2 结果与分析

根据理论模型进行数值计算，所用参数为：光能转化效率η为20%，激励光的光束宽度l为60 μm，光强I为1×108cd.以硅作为样品，其热导率为170 W/(m.K)，热扩散率为8.80×10-5m2/s，光吸收系数β为1.5×105cm-1.空气作为偏转媒质，其热导率为2.61×10-2W/(m. K)，热扩散率为2.0×10-5m2/s，折射率n为1.

2.1 样品表面空气的温度场与温度梯度

图3表示在阶跃激励光的辐照时，由(17a)式数值计算得到的离样品表面不同距离时空气的温度场随时间变化.由图可知随着激励光辐照时间的增加，样品表面空气的温度快速上升，并且离样品表面越近温度上升越快，这是因为热传导需要时间，并且离表面距离越远达到同样温度所用时间就越久.图4则表示在阶跃激励光的辐照时，由(17a)式数值计算得到的不同加热时间空气的温度场随空间的变化.由图可知离空气/样品界面越远的区域，其温度越低，因为离热源越远则随着热能扩散温度降低.同时，由图3、4均可看出空气的温度场为非均匀分布，即存在温度梯度.

图3 样品表面空气的温度随时间变化 图4 样品表面空气的温度随空间的变化

样品表面空气温度梯度随空间的变化规律如图5所示，样品表面处的温度梯度随时间的变化影响不大，但若增大探测光与表面间距，温度梯度将不断下降同时随x方向扩散.若其它条件相同，光热偏转信号的幅值与偏转媒质中的温度梯度成正比.因此，在实验时使探测光接近样品表面可得到更大的光热偏转信号幅值.

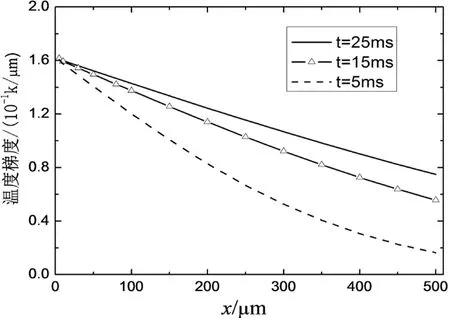
图5 样品表面空气的温度梯度随空间的变化

2.2 以空气作为偏转媒质时的光热偏转信号

图6为光热偏转时变信号幅值随探测光离样品表面为不同距离时的变化情况.由图可知随着探测光离样品表面距离的增加，信号的幅值不断下降，这是因为随着距离的增加温度梯度下降.为了比较探测光离样品表面不同距离时信号上升和下降的快慢，对光热偏转时变信号进行归一化处理，如图7所示，随着探测光离样品表面距离的增加，信号上升和下降速度减慢，同时离样品表面越远，信号幅值趋于饱和所需时间越长.

图6 探测光离样品表面不同距离时的时变信号 图7 探测光离样品表面不同距离时的归一化时变信号

2.3 样品的热扩散率对光热偏转信号的影响

图8为探测光与样品表面的距离为100 μm时，光热偏转信号幅值随热扩散率的变化情况.信号幅值随着热扩散率的增加，其上升、下降速度明显加快，且趋于饱和所需时间越短.这是因为热扩散率越大，热量传导速度就越快，温度场达到稳态所需时间就越短，信号幅值趋于饱和所需时间也就越短，所以样品的热扩散率对信号的变化有显著的影响.

图8 不同热扩散率的归一化时变信号

3 结论

本文构建阶跃光激励的光热偏转技术的一维理论模型，应用拉普拉斯变换法求得样品内及样品表面空气的温度分布和光热偏转信号的表达式.分析样品和样品表面空气的温度场及温度梯度随时间和空间的变化规律，温度场和温度梯度的分布是不均匀的，离样品表面越远其值越小.讨论不同的热扩散率对光热光偏转信号的影响，信号幅值随着热扩散率的增加，其上升、下降速度明显加快，且趋于饱和所需时间越短.该研究对阶跃光激励的光热偏转技术的实验及应用具有一定的价值.