幂零矩阵下二次矩阵方程AXA=XAX的反交换解*
叶祥兴,蒋明谕,刘 佳,韩蕊,陈小燕
(1.赣南师范大学 a.数学与计算机科学学院; b.赣南师范大学 图书馆,江西 赣州 341000;2.瑞昌市第二中学,江西 瑞昌 332200)
1 引言
令A是一个n×n的幂零矩阵,本文的目的是找到二次矩阵方程
AXA=XAX
(1)
的所有反交换解.这个非线性方程也被称为Yang-Baxter型矩阵方程,因为它在形式上与经典的Yang-Baxter矩阵方程[1-2]相似.Yang-Baxter方程出现在物理学和数学的许多分支中,如统计物理学、场论和低维量子可积系统、量子群、三维拓扑、纽结理论等.
Yang-Baxter型矩阵方程有2个平凡解X=0和X=A,但当A为任意矩阵时,找到方程(1)的非平凡解是比较困难的,这是因为解方程(1)就是解一类二次多项式方程组.最近几年,对矩阵方程(1)找到了部分解[3-9].大部分研究结果是基于A满足一定条件时求出方程(1)的所有交换解.例如当A为指数为3的幂零矩阵,在满足可交换条件AX=XA时文献[10]求出方程(1)的交换解结构,当矩阵A为任意的幂零矩阵,满足相同可交换条件时文献[11]给出了方程(1)的交换解结构.当矩阵A为指数为3的幂零矩阵,在满足可交换条件AX=-XA时文献[12]给出方程(1)的所有反交换解的结构.若A为任意的幂零矩阵,本文主要目的是找到方程(1)的所有反交换解.
2 A为若尔当块
由文献[13]引理3.1可知若J是A的若尔当标准型,则求解方程(1)可以转化为求解下列简化的方程
JYJ=YJY
(2)
令B为方程(1)的解、K为方程(2)的解且B=UKU-1,U满足A=UJU-1,若AB=-BA,则JK=-KJ.

其中有关于特征值λ的t×t个若尔当块.若特征值为0,则对应若尔当块Jt(0)满足Jt(0)t=0.


(3)
或

(4)
其中k1,...,kv为任意的复数.
证明令K= ⎣kij⎤,容易得到Jm(0)K的第(i,j)项为ki+1,j,i=1,…,m-1,j=1,…,n,第(m,j)项的所有元素为0,同样-KJn(0)的第(i,j)项为-ki,j-1,i=1,…,m,j=2,…,n,第(i,1)项的所有元素为0.通过计算得到Jm(0)K=-KJn(0)的充要条件为
ki,j-1=-ki+1,j=ki+2,j+1=-ki+3,j+2=ki+4,j+5=-ki+5,j+6=…其中i=1,…,m,j=2,…,n.
且主对角线以下元素全为0.因此K由(3)(4)给出,其中ki≡k1i,i=1,…,v.
若AB=-BA,则B是方程(1)的解的充要条件为B(A-B)A=0.若AB=-BA=-A2或AB=-BA=-B2,则(A-B)A=0或B(A-B)=0.当J=Jn(0)时,由此可以算出方程(2)的反交换解,用下面这个定理来表示.
定理1当J=Jn(0)时,方程(2)的所有反交换解为


(5)
其中c和d为任意的数.
证明当n=2和n=3时容易验证,这里假设n≥4,由引理1知满足JK=-KJ的解K的结构如(3)和(4)所示.已知K(J-K)J=0.当n为奇数时,
计算可得K(J-K)J第一行元素分别为:

因为K(J-K)J=0,则k1=0,k2(1+k2)=0,则k2=0或k2=-1;k3,k4,…,kn-2都为0,kn-1,kn为任意的数,则K的结构如(5)所示.当n为偶数时,用类似方法得到
计算可得K(J-K)J第一行元素分别为:

因为K(J-K)J=0,则k1=0,k2(1+k2)=0,则k2=0或k2=-1;k3,k4,…,kn-2都为0,kn-1,kn为任意的数,则K的结构如(5)所示.
3 A为任意幂零矩阵
令A为指数为z(z>1)的任意幂零矩阵,z为满足Az=0的最小整数.我们简化符号,把矩阵A的若尔当标准型J写成
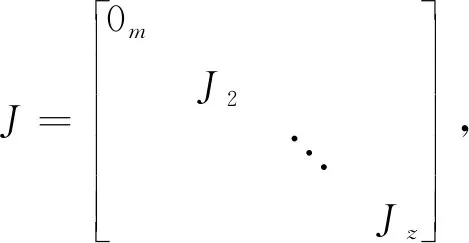
其中0m表示m×m的零矩阵,若尔当块Jt(0)为t×t的,Jt中含有st个Jt(0).为了求解方程(2),按照J的形式将矩阵K分块,令K为z×z的块矩阵即
3)加强基础学校与科研机构、企业单位的对接。课堂不是学生进行学习的唯一途径,学校可以定期邀请科研人员、企业人士对学生进行培养指导;同时,学校应为对特定领域感兴趣的学生提供接触相关专业知识、器材的途径,让学生在较低年龄即可初步接触专业问题及情境。

(6)
其中K11是m×m的,Kii是isi×isi,i=2,…,z.因为
由JK=-KJ可得
得到上述方程组后,依次计算.首先分析方程JtKt1=0,t=2,…,z.将矩阵Kt1分块得到
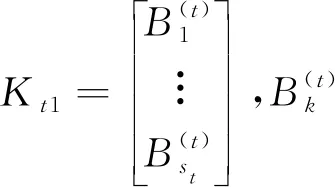
则


用同样的方法解方程K1tJt=0,t=2,…,z,将矩阵K1t分块得到

计算可得
现在来解方程JiKij=-KijJj,i,j=2,…,z,将Kij分块得

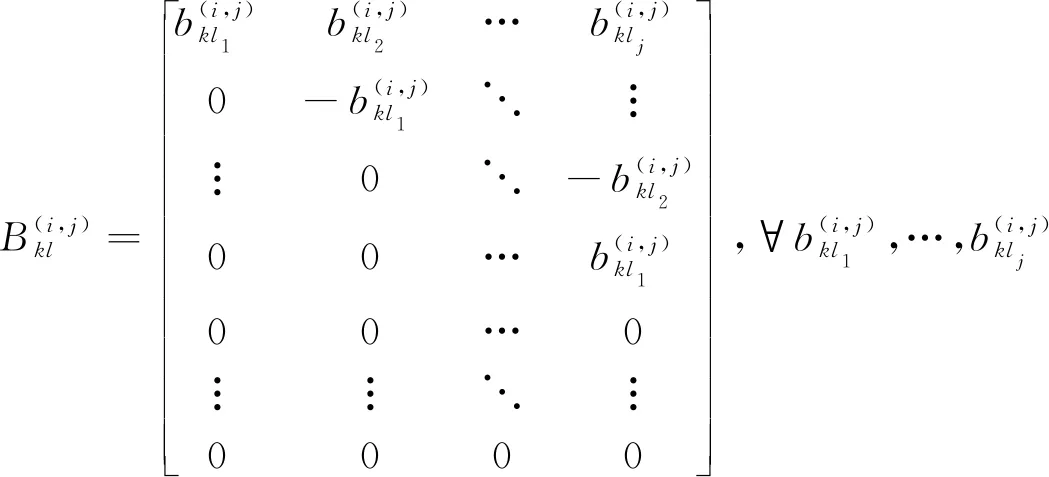
(7)
i>j且j为偶数时,

(8)
i≤j且i为奇数时,
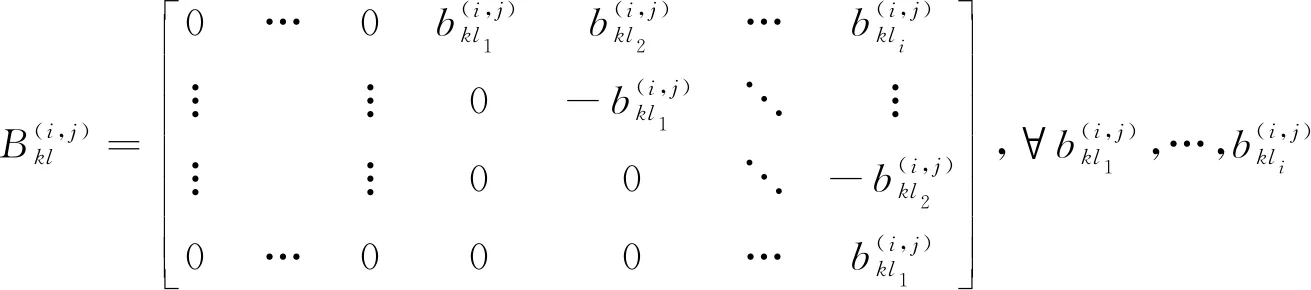
(9)
i≤j且i为偶数时,
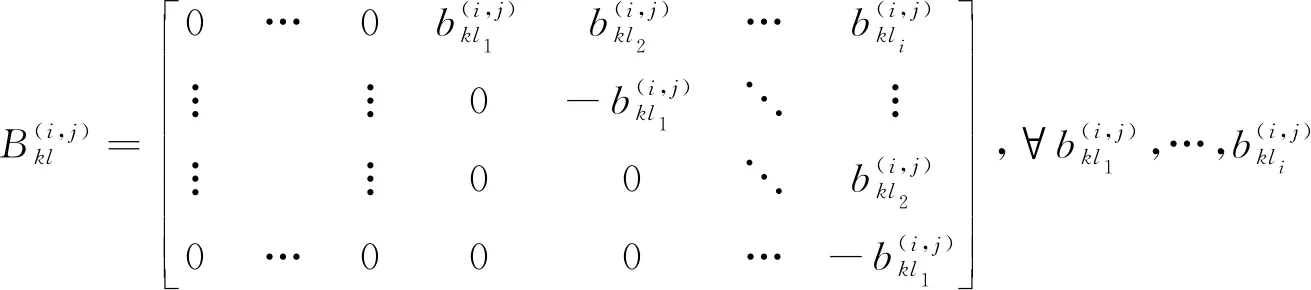
(10)
找到方程JK=-KJ的所有解后,再求解方程K(J-K)J=0.因为

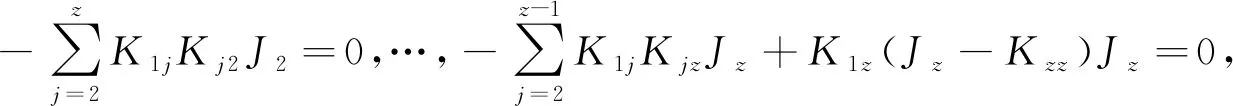

定理2令A为指数是z的幂零矩阵,A=UJU-1,其中J为A的若尔当标准型,则方程(1)的所有反交换解为B=UKU-1,其中K是z×z的且结构如(6)所示,满足:

(11)
4 数值例子
第3节已经给出了任意幂零矩阵下的Yang-Baxter型矩阵方程的反交换解的表现形式,本节给出2个具体例子来更直接的说明主要结果.
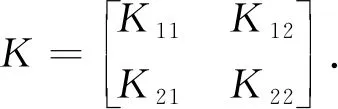


(12)
依次求解方程组(12),其中第1个方程的解在例1中给出,通过求解第2个方程可得q11t11=0,求解第3个方程可得t11z11=0,求解第4个方程可得t11=0,z11q11=0.v11是任意的,当z11=0时,q11是任意的;当q11=0时,z11是任意的.因此Yang-Baxter型矩阵方程(1)的反交换解为

其中k,d1,d2,b1,b2,c11,h11,f11,w11,v11为任意复数.
5 结论
对于非线性矩阵方程(1),当A为任意幂零矩阵时,通过求解JK=-KJ找到K的结构,在求解等价方程K(J-K)J=0进而找到了(1)的所有反交换解.但是对于一个任意的幂零矩阵,找到方程(1)的所有非交换解是十分困难的,因此这将是未来研究的一个方向.

