基于动力响应的特高压变压器套管地震实时损伤识别

陆 军, 朱 旺, 谢 强

(同济大学土木工程学院,上海 200092)

0 引言

特高压输电工程作为生命线工程的重要组成部分,其安全稳定的运行是社会经济稳定发展和民众生活幸福的重要保障。由于独特的能源分布特征与地理环境,我国的特高压输电工程大多位于或途经地震高发区域[1],地震及其次生灾害对变电站设备影响较大。在地震灾害发生后,灾害应急救援体系中电力应急体系是整个救援的基础,震后快速恢复供电是整个救援的难点所在[2]。

2008年汶川地震之后,电力设备的抗震问题引起了专家和学者们的重视,国内电力设备抗震相关研究开展较多,但是前期的研究多聚焦于单体或耦联设备的抗震性能以及减隔震措施上[3-5],对于变电站或区域电网整体抗震韧性提升以及地震发生后应急响应与快速恢复供电措施的研究,目前还处于起步阶段。

变压器套管常采用瓷质材料,强度较低且属于脆性材质,变形能力较差。套管通过连接法兰和升高座与变压器箱体固定连接,整体为悬臂梁结构,自振频率较低,在地震作用下易产生较大响应[3]。震害统计资料显示,在各类地震灾害发生后,变电站中各类套管设备是受损率最高的设备类型之一[6],随着电压等级的增大,特高压变压器套管的地震易损性也在提升。图1(a)为某典型特高压变压器,图1(b)为汶川地震后,灾区变电站内受地震作用而开裂的变压器套管底部金属法兰。地震作用下套管结构产生开裂等损伤,会严重影响设备后续的正常工作,为震后电网运行埋下隐患。若在震后采用人工手持探伤设备对套管进行损伤检测,在灾害发生后第一时间抢修,人力必然匮乏,难以实现快速排查。因此,若将结构的损伤识别技术运用于变电站设备,使用地震时监测到的设备响应对其进行损伤识别与震后快速评估工作,将大大提高震后抢修复速度,提升电网抗震韧性。

图1 特高压变压器Fig.1 The UHV transformer

结构损伤识别领域的研究起步较早,目前工程上大多应用于建筑、桥梁等结构的健康监测项目[7]。结构损伤识别通常可以分为基于结构参数的损伤识别[8-9]、基于响应信号处理的损伤识别[10-11]、基于模型修正的损伤识别[12]以及基于智能算法的损伤识别[13-14]四大类,其中基于响应信号处理的损伤识别方法最适用于本文所研究的变电站设备实时损伤识别问题。这类方法通常基于结构的振动响应信号,采用信号处理算法如小波变换(Wavelet Transform,WT)[15-16]、希尔伯特黄变换(Hilbert-Huang Transform,HHT)[17]、卡曼滤波(Kalman Filtering,KF)[18]等对结构振动响应信号进行处理,寻求信号中包含的损伤特征,并实现损伤识别。

本文以特高压变压器套管为研究对象,基于改进HHT方法提出地震实时损伤识别方法,并通过数值算例进行时程分析,验证该识别方法的准确性。

1 地震实时损伤识别方法

1.1 改进HHT变换

HHT是一种经典非平稳信号处理算法,主要由两部分内容组成:经验模态分解(Empirical Mode Decomposition,EMD)和希尔伯特变换(Hilbert Transform,HT)[19]。在经典信号处理算法中,傅里叶变换难以解析非平稳信号的时频局部特征,小波变换往往面临选择合适小波基函数的困难,而HHT则克服了上述短板,在非平稳随机信号的处理领域具有独到的优势。

HHT提出后便引起了广泛关注,随着研究的日益深入,学者们发现EMD本身存在诸如模态混叠效应的不足之处,后续又提出了许多改进算法。集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)是由黄锷团队提出的针对模态混叠问题的改进算法,通过给信号加入等长白噪声,利用白噪声的零均值特性来消除模态混叠效应[20]。改进后的HHT过程如下:

(1) 将与目标信号等长的白噪声w(t)加入目标信号x(t):

y(t)=x(t)+w(t)

(1)

(2) 对合成信号y(t)进行经验模态分解,得到n阶本征模态函数(Intrinsic Mode Function,IMF)和对应余量Rn(t):

(2)

(3)重复步骤(1)与(2),分别添加不同白噪声信号并进行EMD分解,重复N次。

(4) 将得到的N组IMF分量集合,按照对应阶数取平均,作为目标信号最终的第i阶IMF:

(3)

得到各阶IMF之后,令IMFi=zi(t),对其进行希尔伯特变换,得到:

(4)

进一步构造信号zi(t)的解析信号:

(5)

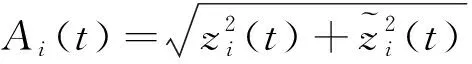
1.2 地震实时损伤识别方法

地震过程中结构产生损伤的瞬间,局部的刚度突变会使得其加速度响应中的高频成分瞬时增加。利用结构动力响应的这一特性,本文提出了一种基于加速度响应信号实时识别地震过程中套管结构损伤的方法。具体步骤如下:

(1) 采集套管结构在地震过程中的加速度响应信号x(t),对其进行高通滤波,得到滤波后的信号y(t)。由于常见电气设备的结构基本频率都低于33 Hz[21],此处将高通滤波阈值设为50 Hz,以此滤除信号中由于结构正常振动响应产生的频率成分;

(2) 对滤波后的信号y(t)进行EEMD分解,为了进一步保留信号中与损伤相关的高频成分,只取分解后的第一阶IMF进行后续变换。通过希尔伯特变换,可以得到与加速度信号对应的时间向量t、瞬时频率向量f和一个m×n阶的瞬时能量矩阵HS。其中,矩阵HS的列数n与时间向量t等长,行数m与频率向量f等长,矩阵中的元素eij代表信号在时刻t(j)、频率f(i)的瞬时能量成分;

(6)

(3) 对矩阵HS进行数据变换。由于在结构振动测试时常用的加速度传感器采样频率为256 Hz,导致HS矩阵中数据量过大,不易判定，因此将矩阵HS按照式(7)进行聚拢。高频成分能量和向量Ehf表示地震持时范围中每一秒内加速度信号中的高频成分能量和:

(7)

式中:imin和imax分别表示时间向量t中大于整数(i-1)的最小元素值对应的下标索引和小于等于i的最大元素值对应的下标索引;

(4) 为找出高频能量和向量Ehf中的异常数据,根据统计学中的箱型图定义法,定义数据异常上限λ:

λ=n(Q3-Q1)

(8)

式中:Q1为向量Ehf中全部元素的下四分位数;Q3为向量Ehf中全部元素的上四分位数;n表示向量Ehf的长度。

搜寻异常值的规则定义为:找出向量Ehf中所有大于λ的元素,将其对应的时间定义为损伤时刻DT。按照此规则,若未能从信号中识别出DT,则表明结构未发生损伤;否则DT表示损伤可能出现的时刻。

(5) 根据步骤(4)的识别结果,若识别出设备发生损伤,则需进一步确定损伤位置,定义高频能量比作为损伤位置特征值DL:

(9)

式中:∑Ehf为信号的高频能量总和;∑Ei为未滤波的对应原始加速度响应信号的能量和;DL表示该位置加速度信号在损伤时刻的能量和与地震持时范围内的能量总和之比。最后将设备上所有加速度传感器采集信号的DL值进行比较,比值越大表示该位置距离损伤实际发生的位置越近。

2 数值试验

2.1 模型简化

为了进一步研究与验证本文提出的损伤识别方法,结合特高压套管的结构特点,将套管结构简化为一10层悬臂剪切模型,并进行数值试验。特高压套管的构造如图2(a)所示,实际工程中套管是安装于变压器箱体之上的,图中用支架代替。以总体质量和基本频率与真实套管保持一致为基本简化原则,简化后的理论模型如图2(b)所示。图中10处集中质量均设为450 kg,集中质量所在节点定义为位置1～10；集中质量将结构划分为10个单元,分别命名为k1～k10;层间刚度均设为1×106N/m。由于变压器套管顶部导线连接属于柔性连接,在地震作用下设备的响应由其自身动力特性主导,柔性连接件的约束作用不明显[22],因此简化过程中仅将其等效为集中质量考虑。

图2 特高压变压器套管Fig.2 The UHV transformer bushing

2.2 输入地震动

数值模型采用Newmark-β法进行动力时程分析,地震动输入选择结构抗震领域常用的 El-Centro波,将地震动加速度峰值归一化后调幅为0.4g,水平单向输入模型。图3为El-Centro波的加速度时程图像。

图3 El-Centro 地震动时程Fig.3 The time histroy of El-Centro ground motion

2.3 工况设置

结构在振动中产生损伤并出现裂纹,往往会导致损伤位置的局部刚度降低,但不会引起质量变化。基于这一特点,以往研究中常采用结构单元的刚度折减来模拟损伤的发生[9-10]。在本文数值试验的工况设定中,采用同样的方法模拟结构在不同时刻的损伤情况。

试验工况一共设定5组:工况1中结构未发生损伤,作为其余各损伤工况的对照组;其余4组工况设定为不同的损伤情况。试验全部工况如表1所列。

3 识别结果讨论与分析

3.1 损伤时刻识别

按照表1各工况对数值模型进行地震动模拟,计算结构不同位置的加速度响应时程后,按照本文提出的损伤识别算法进行识别。首先识别各信号中的损伤时刻DT,结果如表2所列。

表1 数值试验工况

由表2可知,工况1未损伤状态下的结构加速度响应数据均未识别出DT,表明此结构在本次地震动作用下未发生损伤，其余四组工况下识别结果与预设损伤状态一致,均在对应损伤时刻准确识别出了DT。由表2中结果还可以看出,在所有损伤工况中都只有与预设损伤单元相邻的两个位置识别出了损伤时刻DT,这为后续损伤定位提供了极大的便利。

表2 不同工况识别到的损伤时刻DT(单位:s)

3.2 滤波希尔伯特谱

将数值模型的加速度响应按照本文所提出的损伤识别方法进行处理,根据计算所得瞬时能量矩阵HS,可以绘制出加速度响应的滤波希尔伯特谱(图4)。从图4中可以观察到信号的瞬时能量在时域和频域的分布特征。

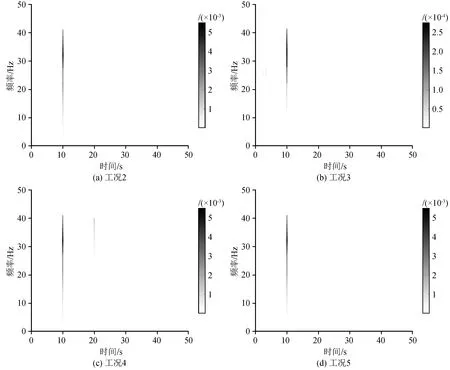
图4 各工况下位置3加速度响应的滤波希尔伯特谱Fig.4 Filtered Hilbert spectra of acceleration responses at location 3 under different working conditions

对比不同工况下结构加速度响应的滤波希尔伯特谱可以发现,在预设损伤工况下损伤位置附近的信号滤波希尔伯特谱中出现了远超套管结构基本频率的高频成分,并且出现的时间与预设损伤时刻对应,而这个特征在未损伤结构的加速度响应谱图中没有出现。这证明结构的突发损伤会在加速度响应信号中产生瞬时高频成分,可以利用这一特征进行套管的实时损伤识别。

工况2设定为地震过程中k3单元突发损伤,对应位置3的加速度响应信号滤波希尔伯特谱如图4(a)所示。从图中可以看到,在10 s时信号中突然出现了异常高频成分,由于高频成分持续时间较短,故将其命名为瞬时高频带。瞬时高频带对应时刻与此工况中预设损伤时刻一致,进一步验证了突发性结构损伤与响应信号中高频成分的对应关系。

工况3设定为k3单元发生轻微损伤,对应位置3的滤波谱图如图4(b)所示,在10 s时同样出现了一条瞬时高频带,这表明轻微程度的损伤也会在结构响应信号中产生瞬时高频成分。进一步对比图4(b)与图4(a)可以看出,结构的损伤程度降低,对应位置加速度信号中瞬时高频带的能量量级也随之变小,这表明可以通过瞬时能量的量级定性判断损伤程度。

工况4设定为结构在单次地震中同一处发生多次损伤,从图4(c)对应谱图中可以看到,加速度信号在10 s和20 s处分别出现了两条瞬时高频带,这两处分别对应两次模拟损伤出现的时间。

工况5设定为套管结构在单次地震中不同时刻不同位置分别出现两次损伤。图4(d)为位置3的加速度响应滤波希尔伯特谱,从图中仅能看到10 s处的瞬时高频带,这是因为第二次损伤发生在k8单元,损伤造成的高频能量未能传递到位置3。进一步绘制出所有位置的谱图,结果表明位置7与位置8的响应滤波希尔伯特谱中20 s处出现了高频带,这验证了以响应信号中异常高频成分作为损伤特征的准确性。

3.3 损伤位置特征值

识别出损伤时刻DT后,进一步对信号进行处理,计算得到工况2～工况5四组损伤工况中,套管结构不同位置加速度响应的损伤位置特征值DL,结果如图5所示。从图5可以看出,距离损伤位置越近,高频能量占比越大,DL值也越大,DL最突出的位置即为最有可能发生损伤的位置。在工况2、3、4中,仅有位置2和位置3两处的损伤位置特征值较为突出,这表明这三组工况中最有可能发生损伤的区域位于位置2和位置3之间,这一识别结果与预设工况一致。

图5 损伤位置特征值识别结果Fig.5 Identification results of damage location eigenvalues

工况5中共有4处加速度信号的损伤位置特征值较大,分别是位置2、3、7、8,这表明在此工况中最有可能发生损伤的区域有两处,分别位于位置2和3之间以及位置7和8之间,这一结果同样与预设损伤情况一致。

损伤位置的识别结果表明,通过本文所提出的损伤识别方法计算结构加速度响应的损伤位置特征值,可以准确判定结构在地震过程中发生损伤的位置。

4 结论

本文提出了适用于特高压变压器套管的地震损伤实时识别方法,并通过数值算例验证了该方法的准确性,发现通过该方法可以对地震后的套管设备进行损伤判定及定位,得出的主要结论如下:

(1) 套管在地震过程中突发损伤会在结构的加速度响应信号中产生瞬时高频成分,可以由此判定结构是否发生损伤。

(2) 响应信号中瞬时高频成分的能量大小与信号采集点到损伤位置的距离有关,距离损伤位置越近的信号中瞬时高频成分的能量越大。

(3) 所提出的实时损伤算法在不同损伤工况下均能够对套管结构进行准确的损伤判定和定位,并且仅需结构的加速度响应作为输入,数据需求较为简单。