横向非一致地震激励下埋地管道的动力响应分析

代建波, 马 静, 胡成涛, 赵泽文

(1. 西安石油大学 土木工程学院, 陕西 西安 710065; 2. 西安石油大学 机械工程学院, 陕西 西安 710065)

0 引言

油气长输管道分布范围广,承受的外部荷载复杂,地震作用下一旦发生破坏,将造成难以估量的损失,甚至可能会引发火灾和爆炸,其安全性问题受到广泛关注[1-2]。地震波的传播过程具有行波效应,因此研究油气长输管道在非一致地震激励时,管-土相互作用的地震响应具有重要意义。

振动台试验是研究管-土相互作用动力响应的有效试验手段之一。孟海等[3]通过设置层状剪切土箱,探讨了非一致地震激励下有接头埋地管线-土的响应规律及发展变化过程。闫孔明等[4]利用独立控制的双台面大型振动台试验设备研究了三维非一致地震激励作用下地下管线的响应,探讨了管线的加速度、应变以及位移等参数的变化规律。韩俊艳等[5]设计并开展了多点非一致激励下埋地管道的多台阵振动台试验,结果表明非一致激励较一致激励下各箱内管道及其周围土体之间均产生了明显的相对位移。赵密等[6]采用悬挂式连续体模型箱,开展了横向一致激励和非一致激励下砂土自由场土体的振动台试验,结果表明非一致激励较一致激励下土体运动的不一致性引起了更强的土体结构性变化,土体的非线性发展相对较快。李立云等[7]基于多子台台阵系统,分析了一致和非一致地震作用下有无埋地管线时的场地地震响应规律,结果表明非一致激励作用将增大场地土体的相对位移,致使相邻地震动输入点间场地土体受到剪切作用。

有一些学者也基于理论分析和数值模拟对管-土相互作用动力响应进行了相关研究:Germoso Claudia等[8]采用土-管道相互作用的三维(3D)参数模型对埋地管道地震响应进行数值模拟。Liang等[9]构建了管-土界面,模拟了管-土间的耦合效应,结果表明管道的变形明显受到管道周围回填土的制约。刘飞成等[10]基于地下管道建立有限元模型,考虑管-土相互作用和行波效应,综合分析了三向地震动一致激励与非一致激励下的管道动力响应结果。Pan等[11]通过建立三维有限元模型,研究了地下空间相关地震运动对大跨度埋地管道地震行为的影响。吴祚菊等[12]为了研究考虑地震动的空间相关性时埋地管线的地震响应,基于Opensees有限元程序,对埋地管线在多维多点相关地震动作用下的响应进行数值模拟,结果表明了在抗震设防等级较高的地区,考虑非一致地震激励作用对于埋地管线的破坏是非常必要的。

综上所述,一些学者已经进行了非一致激励下埋地管道的地震响应研究,结果表明了管道进行横向、纵向、双向和多维地震激励研究的必要性;非一致激励相对一致激励时对管道和管周土体产生的地震响应更大,且管-土相互作用更为复杂,对管道进行地震响应研究时考虑非一致激励是非常有必要的;埋地管道的地震响应分析和设计集中在对结构轴向应变的评估,仅考虑纵向地震动作用的影响,忽略了由横向地震动作用引起的结构弯曲应变,结果可能是不适用的。以上代表性文献在进行试验和分析时,对地震时管道和管周土体在振动状态的模拟采用了分段土箱试验、连续土体考虑边界效应等试验方案还可进行进一步优化和改进。本文研发了可以实现土体双向层状剪切变形效应的层状剪切型连续体模型箱,采用增加管道内压模拟管道运行状态,通过进行横向非一致地震激励下埋地管道的有限元分析和振动台试验,对比研究管-土相互作用地震响应规律。

1 有限元模型建立

1.1 单元类型及相关参数的确定

为研究非一致地震激励下管-土相互作用动力响应规律,选取管道尺寸为1 422 mm(直径)×33.3 mm(壁厚)×100 m(长度)的埋地油气长输管道进行分析;管周土体尺寸设置为6 m×8 m×100 m。

模型中的管道、土体均选用C3D8八结点线性六面体单元,该单元在弯曲荷载下不易发生剪切自锁现象,且位移结果比较准确。建立的管道和土体分析模型如图所示。

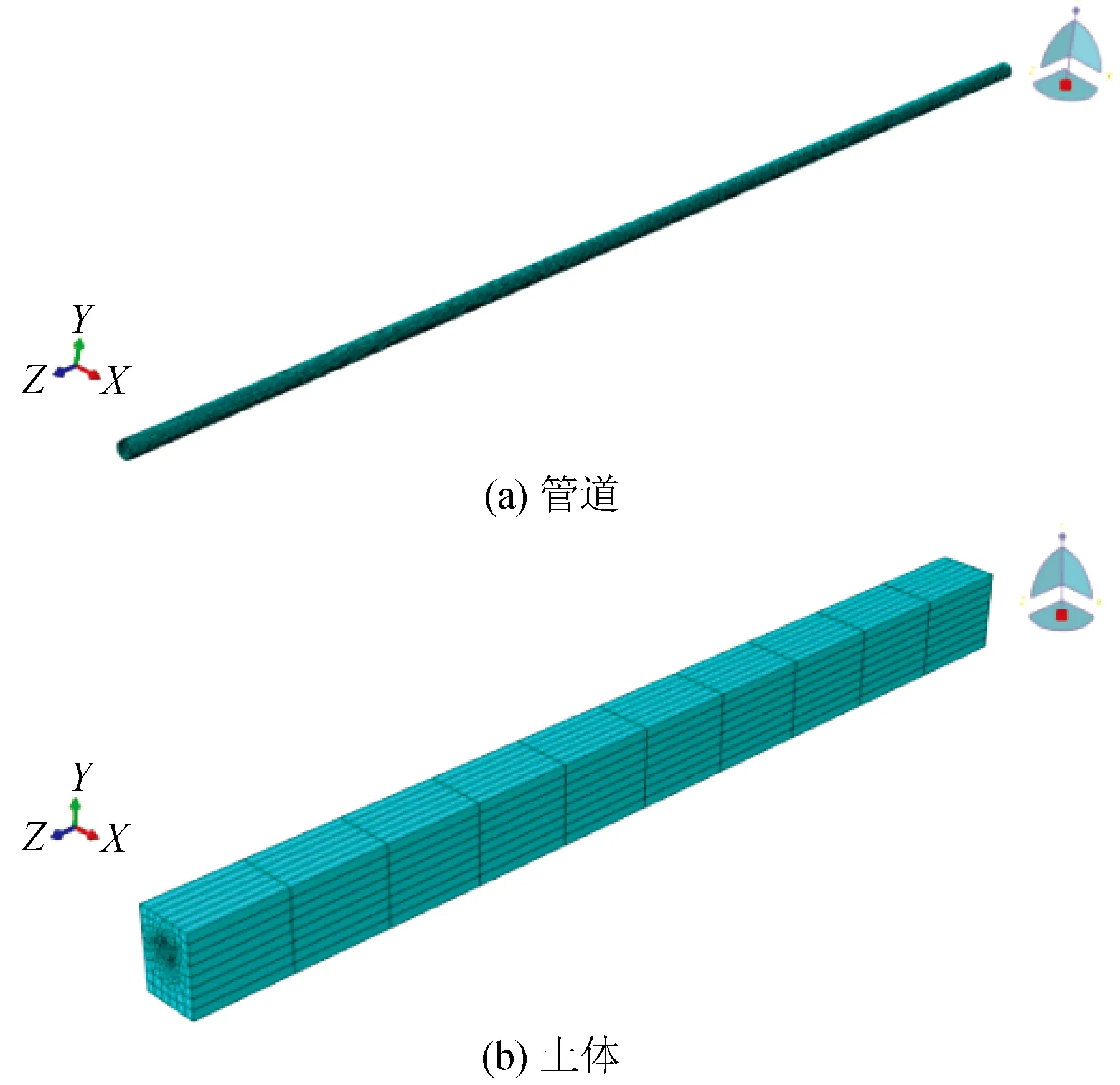
图1 管道和土体模型Fig.1 Pipeline and soil model

在对管-土相互作用进行分析时,涉及管道、土体的密度、弹性模量和泊松比等参数,其具体数值如表1所列。

1.2 管-土接触单元设置

管-土界面采用非线性接触模型,即通过对管道与周围土体之间加入接触单元,定义接触单元不同的本构关系来模拟管-土相互作用。由于埋地管道和周围土体的物理特性差异较大,易在剪应力或切向应力下出现相对滑动或脱离现象,因此通过在管道和土体之间设置一种厚度为零的接触单元,以模拟研究管-土界面上的这一变形特征。目前,罗佩等[13]提出的无厚度Goodman 4节点8自由度单元可以较好反映切向应力变化和变形所产生的非线性特征。

在分析管-土接触时,可以认为其接触面的法向压力无穷大,但相互不贯穿,脱开时法向压力为零,定义为脱开状态,法向约束失效,这种法向行为在有限元分析中可以用“硬”接触模拟。

表1 管道及管周土体相关参数Table 1 Parameters related to pipeline and surrounding soil

接触面的切向行为可以用摩擦模型模拟,其摩擦系数可以用式(1)来表示。当接触面存在法向接触压力P时,在接触面上可以传递切向应力,也称为摩擦力,当摩擦力等于切向摩擦力极限值τcrit时,认为接触面处于黏附状态,并用式(2)库仑摩擦模型计算这一极限剪应力,当摩擦力大于τcrit之后,接触面上就开始产生相对滑移变形,称为滑移状态。理想状况下,接触面在滑移状态前是不会发生剪切变化的,可以引入一个“弹性滑移变形”概念用来确定接触面的协调性,在有限元模拟中可以用接触单元的罚刚度k值表示。

μ=tan(0.75φ)

(1)

τcrit=μp

(2)

式中:τcrit为切向摩擦力极限值;μ为摩擦系数;p为法向接触力;φ为内摩擦角。本文模拟分析将管-土接触面的切向行为设为“罚”接触,法向行为设为“硬”接触。

1.3 边界条件

埋地管道与管周土体可以视作一个半无限体,对这一半无限体建立管-土地震耦合响应有限元分析模型,这是研究管-土地震耦合响应规律的核心。由于通过人工截断的管-土地震耦合响应模型的反射波会在土体中快速消散,因此需要同分析静力结构一样设置刚性支撑或在截断的边界处设置阻尼器,吸收法向和切向两个方向扩散的能量。在有限元数值模拟中,常用黏性人工边界和黏弹性人工边界来模拟这一问题[14]。通过MATLAB软件对三维黏弹性动力边界条件进行编程,计算得到各个面法向及切向的弹簧刚度和阻尼器系数(表2),并依次添加在各个面的耦合点上,施加完成后的管-土人工截断模型边界如图2所示。

表2 弹簧刚度及阻尼器系数取值

2 振动台试验简介

2.1 试验土箱、材料及相似比确定

本次试验在水平双向地震模拟振动台阵系统上进行。该系统振动台台面尺寸均为1 000 mm×1 000 mm,相距2 000 mm,单个振动台承受加载重量可达5 t,且实现X、Y向双向加载。

图2 弹簧-阻尼器模拟图Fig.2 Simulation diagram of spring-damper

为了更好地模拟非一致地震激励下土体所产生的剪切变形以及管道在土体中的连续状态,研发了层状剪切连续体模型土箱。该土箱由三部分组成,左右两个部分土箱完全相同,分别置于两端的台面上,然后通过铰接装置连接中间土箱,以确保每个部分可实现自由伸缩;在中间土箱底部和各层框架之间放置牛眼滚珠,以承担箱体的自重和实现层间错动。为了防止振动台工作时土体渗出,在箱体内壁贴有厚度为1 mm的橡胶布。组装的试验土箱如图3所示。

图3 层状剪切连续体模型土箱Fig.3 Laminar shear continuum model box

以相似理论为基础,量纲分析为依据,对本次试验相关的管道和土体进行了其物理特征参数的相似关系处理[15]。在相似关系的设计中,管道和土体分别采用完备模型和忽略重力模型,最终得到了试验模型材料的长度相似比Sl、弹性模量相似比SE、密度相似比Sρ、应力相似比Sσ、应变相似比Sε、频率相似比Sf、加速度相似比Sa和重力加速度相似比Sg。其数值如表3所列。

表3 试验模型相似比Table 3 Similarity ratio of the test model

试验模型土体为砂土,经实验测得其密度为1.78 g/cm3,含水率为14.1 %,压缩模量为15.09 MPa,黏聚力为10.6 kPa,内摩擦角为28.5°;试验管道材料为L245直缝电阻焊钢管,测得其基本力学性能如表4所列。在管道内部加压8 MPa以模拟油气运输时对内壁产生的内压(图4)。

表4 管道力学性能Table 4 Mechanical properties of pipeline

图4 管道内压示意图Fig.4 Diagram of the internal pressure of pipeline

2.2 试验方案及传感器布设

为了研究横向非一致地震激励下管-土相互作用的动力响应规律,需在模型箱上布设合理的传感器。如图5所示,M11～M33为土体中加速度传感器布置测点,D11～D33为土体中位移传感器布置测点,沿纵向共三个监测面,左右两个监测面距边界为750 mm,中间监测面距两侧为1 130 mm,每个监测面沿横向分为三个测点,以监测土体的加速度及位移变化情况。

图5 土体加速度及位移传感器布置Fig.5 Layout of acceleration and displacement sensors in the soil

管道加速度传感器监测点如图6(a)所示,沿纵向在管道表面粘贴布设5个加速度传感器,在左右两端的振动台面上布设2个加速度传感;管道应变传感器监测点如图6(b)所示,分为六个监测面,左右两端相距边界380 mm,其余监测面均相距600 mm。

图6 管道加速度、应变传感器布置(单位：mm)Fig.6 Layout of acceleration and strain sensors in the pipeline (Unit:mm)

土体加速度、位移和管道加速度、应变的传感器监测点同数值模拟计算监测点布设一致,1-1剖面如图7所示。

图7 1-1剖面图Fig.7 View of profile 1-1

2.3 地震波选取及加载工况

试验场地类别假定为Ⅱ类场地,其特征周期为0.35 s,共选取两条试验记录波和一条人工合成波进行输入。鉴于篇幅限制,仅选取El-Centro波激励下的管-土动力响应进行分析。

按照我国的抗震规范,抗震设防烈度为7度、8度、9度及9度罕遇地震所对应的加速度峰值分别为0.1g、0.2g、0.4g及0.62g[16]。用于模拟和试验的地震波加速度时程曲线和频谱图如图8所示,实际加载工况列于表5,表中加速度峰值为经过相似比换算的加速度峰值,M-1表示两个振动台输入了同一条波形。

图8 El-Centro波时程曲线和频谱图Fig.8 Time-history curve and spectrum of El-Centro wave

表5 振动台试验加载工况Table 5 Loading conditions for the shaking table test

3 管-土数值模拟及试验对比分析

3.1 地震波的输入

为了突显非一致激励的影响,两个振动台输入地震波时间设置为延迟1 s。如图9(a)所示,本试验采用双台阵地震模拟振动台,进行非一致地震激励时,利用振动台阵控制系统,对两个振动台沿横向(X方向)分别输入同一条地震波,但有一个振动台开始激励时间相对延迟1 s,以实现非一致激励方式,获得非一致激励下的地震响应。而在有限元模型中如图9(b)所示,选取底部左侧RP-3和右侧RP-4两点作为地震波的输入对象,沿X方向分别加载时间间隔1 s的地震波,由此实现非一致地震激励带来的行波效应现象。

图9 地震波加载示意图Fig.9 Seismic wave loading diagram

3.2 管道应变响应分析

如图10和图11所示,分别为横向非一致激励下管道应变云图和管道应变峰值曲线。由图可知,在横向非一致地震激励下数值模拟和振动台试验的管道应变峰值均呈现出中间大两端小的现象,其中间应变峰值最小达到两端的1.6倍左右,且管道应变峰值随着加载等级的增大而增大。当数值模拟加载等级增加到0.4g时,管道应变峰值较0.2g增加了45.9%,当加载等级增加到0.62g时,其应变峰值较0.4g时涨幅了53.4%,涨幅随加载等级的提高处于递增状态,但远低于埋地油气管道的破坏标准。

图10 横向非一致激励下管道应变云图Fig.10 Strain nephogram of pipeline under transverse non-uniform excitation

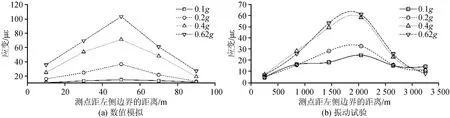
图11 横向非一致激励下管道应变峰值曲线Fig.11 Peak strain curve of pipeline under transverse non-uniform excitation

当振动试验加载等级为0.4g和0.62g时,管道应变峰值相差不大,这是由于随着加载级别的提高,管-土接触面逐步破坏,间距也逐步扩大,且管-土间发生相对滑移,接触面处逐渐接近于自由状态,因此管道峰值应变增加幅度减小。

3.3 管道加速度响应分析

选取管道左侧测点A1为主要分析对象,图12为横向非一致激励不同加载等级下管道时程和频谱曲线。由图可知,数值模拟和振动试验的加速度波形曲线和频谱组成基本一致,频谱峰值均出现在0～10 Hz低频区域;当加载等级为0.4g时,振动试验频谱逐渐出现多峰现象,这是由于振动台试验采用多级加载制度,已完成工况对结构造成的损伤会累积到下一工况,周围的土体发生相应的破坏;当加载等级达到0.62g时,二者频谱曲线表现出多峰现象更为明显,管道的傅里叶频谱也较为丰富,多峰频率由0～10 Hz逐渐向10～20 Hz频域扩散显著。

由此表明,数值模拟和振动试验管道加速度响应虽有差异,但总体来说其响应规律的一致性较好。随着加载等级的逐级递增,加速度响应曲线的多峰值特征明显,频谱丰富,这是由于随着加载等级的增大,约束管道周围的土体破坏加重,地震激励下管道运动更为自由。

图12 横向非一致激励下管道时程曲线及频谱图Fig.12 Time-history curve and spectrum of pipeline under transverse non-uniform excitation

3.4 土体加速度响应分析

基于模型土体的对称性,选取模型箱左侧M21测点为主要分析对象,图13为非一致激励下数值模拟和振动试验土体加速度时程曲线与频谱曲线。由图可知,数值模拟和振动试验测点的土体加速度峰值随着加载等级增加而增大,基本出现在2～5 s时间内,随着加载等级的增大,其加速度响应多峰现象愈加明显,且频谱峰值大多集中在0～5 Hz低频区域内,傅里叶谱组成丰富。当加载等级为0.4g时,频谱峰值明显增大,波峰现象频繁,此时的土体开始受到地震波所产生的破坏,土体更容易表现出非线性特征。

图13 横向非一致激励下土体时程曲线与频谱图Fig.13 Time-history curve and spectrum of soil under transverse non-uniform excitation

综合而言,数值模拟和振动试验的土体加速度响应结果仅在数值大小上存在差异,总体变化规律上具有较好的一致性。

3.5 土体位移响应分析

图14为横向非一致地震激励下不同加载等级土体峰值位移变化曲线。由图可知,数值模拟和振动试验土体位移均随着加载等级的增大而增大,土体位移根据高度的不同所呈现的变化存在差异。在加载等级小于0.4g时,土体位移的峰值变化曲线增长明显,当加载等级大于0.4g时,峰值位移曲线斜率减小,增长减缓。其原因在于土体从低到高所产生的剪切效应随着加载等级的增大更加显著,而在0.4g增加至0.62g时土体受到管道产生的压力,致使土体先被压实随后发生破坏,导致位移变化减小,土体进入非线性阶段。

图14 土体峰值位移随加载等级变化曲线Fig.14 Variation curve of peak soil displacement with loading level

相较于数值模拟,振动试验因累积加载模式产生的影响更为显著,但总体趋势一致性较好。

4 结论

本文通过横向非一致地震激励下埋地管道的有限元分析和振动台试验,对比研究管-土相互作用下管道应变、管道加速度、土体加速度和土体位移响应规律,得出如下结论:

(1) 横向非一致地震激励下数值模拟和振动试验结果的管-土动力响应规律一致性较高,对比分析的结论充分验证了试验结果的可靠性和数值模拟的合理性。

(2) 管道应变峰值均呈现出中间大两端小的现象,其中间应变峰值最小达到两端的1.6倍左右。数值模拟管道应变峰值最大涨幅可达53.4%,而试验加载等级为0.4g和0.62g时,管道应变峰值相差不大,这是由于随着加载级别的提高,管-土接触面逐步破坏,而发生相对滑移。

(3) 在较低等级下数值模拟和振动台试验的管道加速度波形曲线和频谱组成基本一致。当加载等级达到0.4g时,振动台试验先逐渐出现多峰现象,随着加载等级的提高,二者频谱曲线表现出多峰现象更为明显,多峰频率均由0～10 Hz逐渐向10～20 Hz频域扩散,管道运动更为自由。

(4) 土体加速度和频谱峰值均随着加载等级的增大而增大,傅里叶频谱的组成逐渐丰富;土体位移随着加载等级的提高呈现逐级增大的现象,在加载等级增加到0.4g时,位移曲线斜率减小,土体非线性表现明显。