附加黏弹性阻尼与金属阻尼耗能的自复位墙结构抗震性能对比分析
朱晓莹, 吴 浩,2, 周 颖,2
(1. 同济大学土木工程学院, 上海 200092; 2. 同济大学土木工程防灾国家重点实验室, 上海 200092)
0 引言
自复位墙结构是国内外地震工程界的研究热点,可实现震后低损伤并快速恢复使用功能。相比传统结构,其在地震作用下具有更大的变形能力,且几乎无残余位移[1]。自复位墙主要由复位系统和耗能系统构成,在地震作用下形成旗帜型滞回曲线(如图1所示)。复位系统通常由重力和后张拉预应力筋组成,已有研究表明通过后张拉预应力筋可实现墙体的自复位,但耗能能力较低[2]。故自复位墙结构一般需设置附加耗能装置,来提高整体结构的抗震性能。

图1 旗帜型滞回曲线Fig.1 Flag-shaped hysteretic curve
目前,已有多种应用于自复位墙结构中的耗能构件,Smith等[3]在自复位墙与基础接缝处布置耗能钢筋,通过墙体底部接缝的耗能钢筋发生屈服;或在自复位墙片之间和自复位墙与相邻竖向构件之间设置屈服型阻尼器或摩擦型阻尼器[4],通过在竖向接缝处的相对位移允许阻尼器耗能。总之,结合自复位墙结构变形能力强的特点,大量研究者在墙体底部或竖向附加金属阻尼器,通过材料的弯曲屈服、剪切屈服、拉压屈服或摩擦阻尼来增加结构的耗能能力,这些阻尼器在位移达到一定程度时即可发挥耗能作用。自复位墙结构在附加金属阻尼器后可显著减小结构的位移响应,但在地震动强度较小时由于相对变形小,阻尼器尚未发挥耗能作用,使得自复位墙结构在小震下的位移和加速度响应不能得到有效控制[5],从而对非结构构件造成不利影响。
黏弹性阻尼器耗能性能优良、构造简单、小变形下即可发挥耗能作用,目前已广泛应用于建筑结构消能减振工程中[6]。本文拟将黏弹性阻尼器应用于自复位墙结构中,设计一幢10层自复位墙结构,分别采用黏弹性阻尼器和U型金属阻尼器作为附加耗能构件,通过弹塑性时程分析对比两者的抗震性能。
1 原型结构设计
1.1 整体概况
以一幢10层自复位墙结构为例,其平面布置如图2(a)所示,其中自复位墙为抗侧力构件,重力框架为承重构件。底层高为5 m,二层高为4.2 m,其余上部楼层均为3 m,总高33.2 m。

图2 原型结构平面及立面布置Fig.2 Plan and elevation layout of the prototype structure
结构的抗震设防烈度为8度,设计基本地震加速度为0.2g,设计地震分组第二组,Ⅱ类场地,场地特征周期Tg=0.4 s。按四水准抗震设防目标,采用直接基于位移抗震设计方法进行设计[7]。设计中考虑结构在第四水准下的目标位移角为2%,以结构短边方向为例,计算得到每片墙体的设计基底剪力Vd为265 kN,底部弯矩Md为6 147 kN·m。
1.2 黏弹性阻尼耗能的自复位墙设计
(1) 自复位墙设计。对于附加黏弹性阻尼器的自复位墙,其立面布置如图2(b)所示。按照墙体底部抗弯承载力进行设计,则自复位墙底部弯矩由预应力筋、墙体竖向力和耗能构件三个部分共同承担,满足下式关系:
Md=Mp+Mn+Ms
(1)
β=Ms/(Mp+Mn)
(2)
式中:Ms、Mp、Mn分别为设计位移下耗能构件、预应力筋和竖向力对墙体底部弯矩的贡献;β为耗能参数[8]。
设计中取短边方向的自复位墙为例,混凝土材料为C40,预应力钢绞线采用公称直径为15.2 mm的高强低松弛钢绞线。重力框架柱截面为400 mm×400 mm,框架梁采用开槽梁形式,截面为200 mm×300 mm。具体设计结果如表1所列。
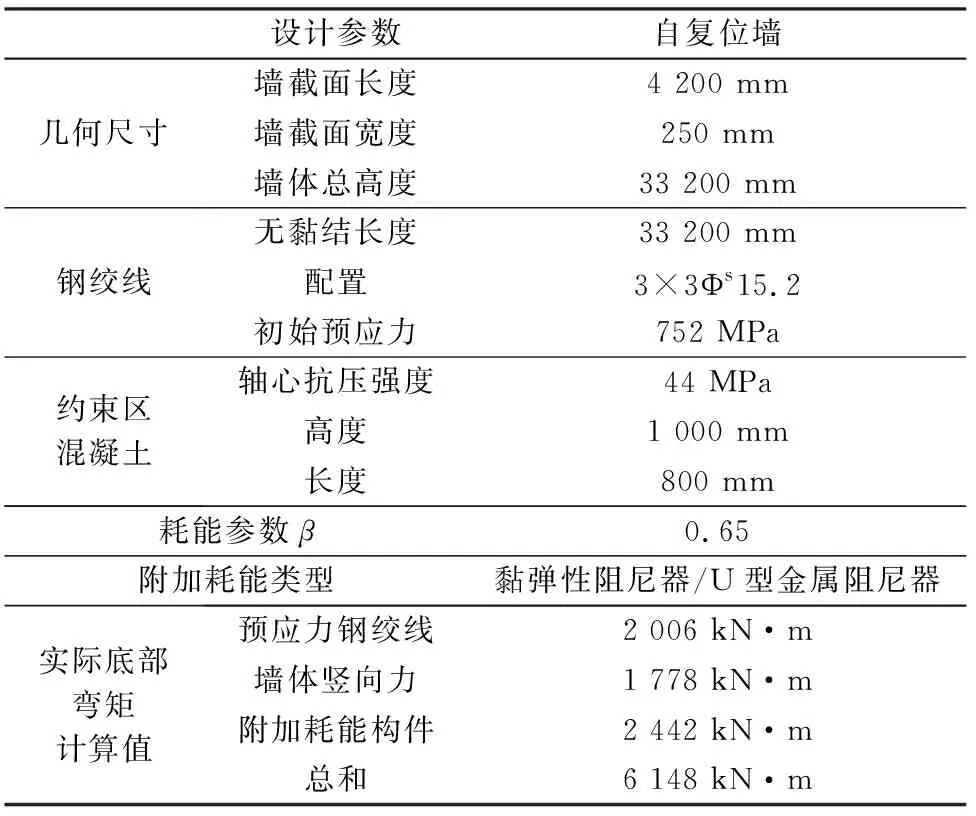
表1 自复位墙设计参数
(2) 黏弹性阻尼器设计。根据自复位墙设计结果,阻尼器需承担底部弯矩为2 442 kN·m。本设计中在每个层高处布置一个黏弹性阻尼器。在结构达到设计目标2%的顶点位移角时,黏弹性阻尼器的剪切变形达到250%的应变幅值。参考周颖等[9]提出的黏弹性阻尼器设计相似准则,依据前期试验与原型结构中阻尼器应变相等,且提供的阻尼力等效这一原则计算。即不同黏弹性阻尼器滞回曲线的力和位移需要满足下面相似关系:
(3)
(4)
式中:u0为阻尼器的最大位移;h为黏弹性材料层的厚度;n为黏弹性材料的层数;A为每层材料的面积;t为试验阻尼器的物理量;p为实际阻尼器的物理量。根据上式计算,取原型结构中每个黏弹性阻尼器含一层黏弹性材料,尺寸为400 mm×250 mm×34 mm。在结构设计目标位移下的阻尼器设计参数如表2所列。
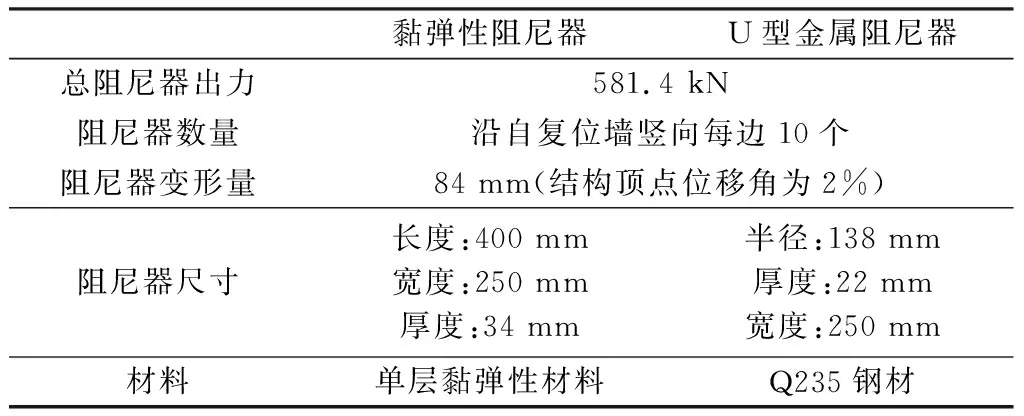
表2 附加耗能构件设计参数
1.3 金属阻尼耗能的自复位墙设计
拟采用附加U型金属阻尼耗能的自复位墙结构进行对比研究。U型金属阻尼器是一种弯曲型金属阻尼器,在低荷载下即可屈服进入塑性状态,从而发挥耗能作用。附加U型金属阻尼器的自复位墙结构设计除阻尼器外,自复位墙的配筋设计均与附加黏弹性阻尼器的自复位墙设计结果一致。
如表2所列,在设计目标位移下,U型金属阻尼器对于底部的弯矩贡献、布置数量和位置均与黏弹性阻尼器相同。U型金属阻尼器的材料选用Q235钢材,参考已有大量试验结果,考虑在结构目标位移角下阻尼器的延性系数为4,屈服后刚度为0.03[10],则U型金属阻尼器的屈服力为51.9 kN。
2 有限元模型及地震动选取
2.1 有限元模型建立
采用OpenSees有限元分析软件,分别建立上述两种不同耗能机制的自复位墙结构模型。如图3所示,采用柔度法梁柱单元模拟自复位墙体,通过设置底部混凝土纤维只受压不受拉模拟墙底接缝的张开。重力柱采用弹性梁柱单元模拟,底部设置为铰接,与自复位墙通过阻尼器单元连接。另外设置右边的重力柱以考虑P-Δ效应,并施加单片自复位墙所分担的楼层荷载。在重力柱的每个楼层节点处与自复位墙节点对水平自由度进行约束。预应力钢绞线采用共转桁架单元模拟,底部引入零长度单元用来避免其受压,顶部通过刚臂与自复位墙节点连接。
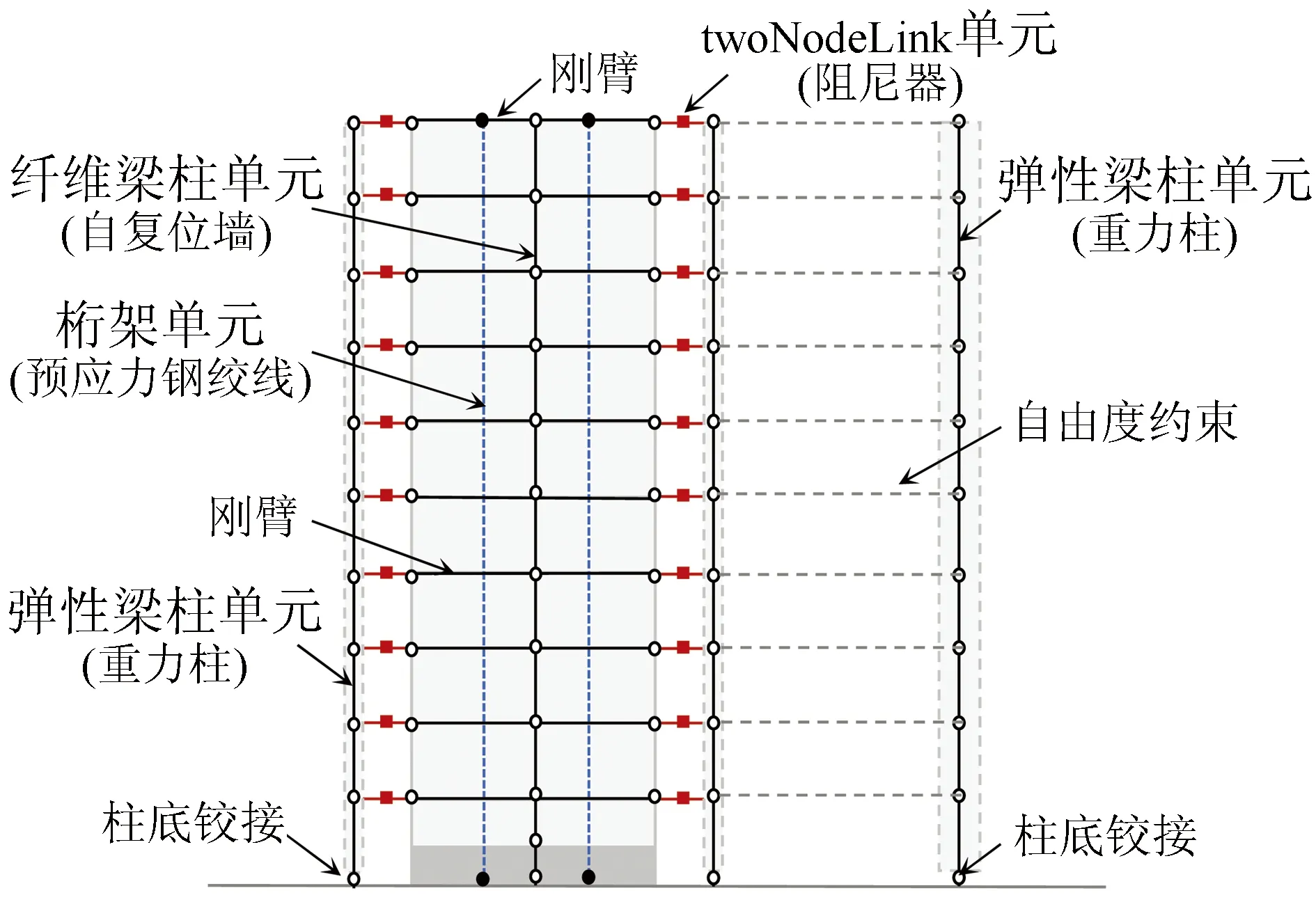
图3 有限元分析模型示意图Fig.3 Schematic diagram of the finite element model
采用TwoNodeLink单元模拟阻尼器试件。对于黏弹性阻尼器,参考周颖等人提出的强非线性力学模型[11]模拟,具体如图4所示,分别定义Viscous、ElasticMultiLinear和Elastic三种单轴材料,再使用Parallel命令将各单轴材料并联起来。对上述1.2节计算中所用的既有试验滞回曲线进行模拟。图5(a)为试验结果与模拟结果的对比。
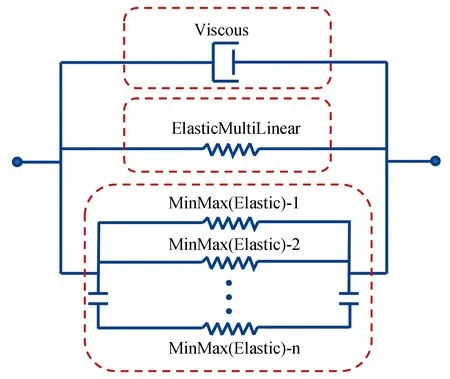
图4 力学模型在OpenSees中的实现Fig.4 Implementation of mechanical model in OpenSees

图5 模拟结果与试验结果对比Fig.5 Comparison between simulation results and test results
U型金属阻尼器的滞回特性通过Steel02材料来模拟,其初始刚度E,屈服荷载Fy按实际计算值设定。为验证建模方法,对一U型金属阻尼器试验[12]进行了模拟,结果如图5(b)所示。最终算例模型中阻尼器采用上述模拟方法,按照设计尺寸进行参数设定。
2.2 地震波选取及调幅
选取FEMA P695中建议的44条远场地震动对结构模型进行弹塑性时程分析。将44条地震动按照我国规范反应谱分别在多遇地震(小震)、设防地震(中震)、罕遇地震(大震)和极罕遇地震(巨震)下进行调幅。使得所选地震波反应谱在0.2倍结构基本周期到2倍结构基本周期范围内的平均值与规范反应谱值误差最小[13]。
3 抗震性能对比分析
3.1 层间位移角
图6给出了附加两种不同阻尼耗能的自复位墙结构在44条地震动作用下的最大层间位移角对比情况,其中横坐标为附加U型金属阻尼器(U-shaped Metal Damper,简称USD)的结构最大层间位移角响应,纵坐标为附加黏弹性阻尼器(Viscoelastic Damper,简称VED)的最大层间位移角响应。可见小震下附加黏弹性阻尼器的整体结构最大层间位移角响应比附加U型金属阻尼器的结构响应小,这是由于黏弹性阻尼器在小变形下即可产生耗能。随着地震强度的增大,中震时所统计的黑色数据点开始较均匀地分布于对角线两侧,说明此时U型金属阻尼器也发生耗能,且两种不同耗能机制的结构最大层间位移角响应接近。进而,大震和巨震下附加U型金属阻尼器的大部分数据点位于对角线的上方,可见在地震动强度较大时,U型金属阻尼器控制结构最大层间位移响应的能力更好。

图6 最大层间位移角对比Fig.6 Comparison between the maximum story drift ratios
图7给出了44条地震动作用下,两种结构层间位移角响应沿楼层分布的中位值和具有84%保证率的值。如图7(a)所示,小震下附加黏弹性阻尼器的结构层间位移角的中位值和84%保证率值均明显小于附加U型金属阻尼器的结构,这充分体现了黏弹性阻尼器小变形下即可耗能的优势。随着地震动强度的增大,中震下两者的中位值几乎重合[图7(b)],这表明本算例中U型金属阻尼器在中震下的耗能能力与黏弹性阻尼器接近。如图7(c)所示,大震下由于上部结构的整体变形较大,两种结构底部楼层层间位移角响应差距不大,但附加U型金属阻尼器的上部楼层结构层间位移角响应小于附加黏弹性阻尼器的结构。巨震下两者之间的差距增大[图7(d)],可见此时U型金属阻尼器的耗能效果要明显优于黏弹性阻尼器。

图7 层间位移角对比Fig.7 Comparison between story drift ratios
3.2 楼层加速度
楼层加速度是考量结构抗震性能的另一项重要指标。图8分别对不同水准下44条地震动分析结果的最大楼层加速度相对于最大地震动输入的放大系数最大值进行了统计,横坐标和纵坐标分别为附加U型金属阻尼器和黏弹性阻尼器的结构最大楼层加速度放大系数。如图8所示,在小震和中震下所得数据点绝大部分位于对角线的下方,表明附加黏弹性阻尼器的自复位墙结构其楼层加速度放大系数最大值要明显小于附加U型金属阻尼器的结构响应,这与黏弹性阻尼器在小震下即可发挥耗能作用有关。随着地震动强度的增大,两种结构的最大楼层加速度放大系数较为接近,数据点沿对角线分布逐渐均匀。
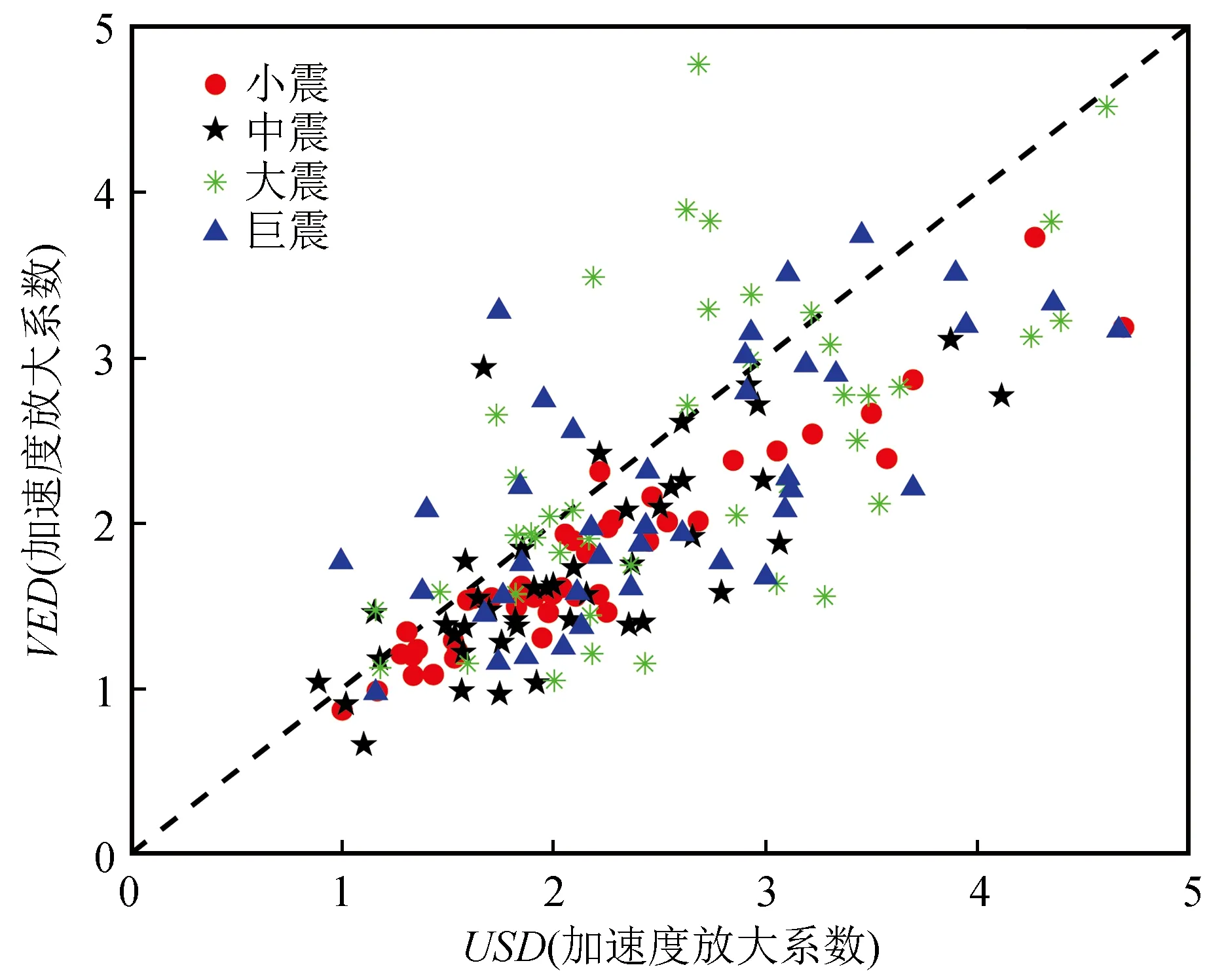
图8 最大楼层加速度放大系数对比Fig.8 Comparison between the maximum acceleration amplification factors
两种结构的加速度放大系数沿楼层的分布情况如图9所示。在小震和中震下,自复位墙结构的加速度响应最大值出现在顶部楼层;同时附加黏弹性阻尼器的自复位墙结构的加速度放大系数明显小于附加U型金属阻尼器的结构[图9(a)和图9(b)]。这是由于在变形较小时,黏弹性阻尼器即可发挥耗能作用,且黏弹性阻尼器的等效刚度小于U型金属阻尼器。随着地震动强度的增大,如图9(c)和图9(d)所示,大震和巨震下自复位墙的底部楼层加速度放大系数明显增大,这可归因于自复位墙底部接缝抬起幅度增大,墙底非线性显著增强。此外,附加U型金属阻尼器的结构加速度放大系数与附加黏弹性阻尼器的结构差距明显减小,这是因为在巨震设计下黏弹性阻尼器和U型金属阻尼器的阻尼力一致,此时两者的等效刚度接近。

图9 楼层加速度放大系数对比Fig.9 Comparison between acceleration amplification factors
3.3 阻尼器耗能
根据上述分析结果,自复位墙结构中附加不同类型的阻尼器,对结构响应有不同影响。如图10所示,为一条地震动作用下自复位墙原型结构中顶部楼层右侧阻尼器在不同地震强度下的力-位移曲线。如图10(a)所示,黏弹性阻尼器在小震下已产生耗能,并且随着地震动强度的增大其阻尼力逐渐增大,但整体上滞回曲线比较狭窄,耗能能力有限。相同地震波和位置处U型金属阻尼器的力-位移曲线如图10(b)所示,可见在小震阶段阻尼器处于弹性阶段,此时尚未发挥耗能作用;在中震作用下U型金属阻尼器开始屈服,但耗能有限;随着地震动强度的增大,在大震和巨震作用下的滞回曲线更加饱满,耗能作用突出。
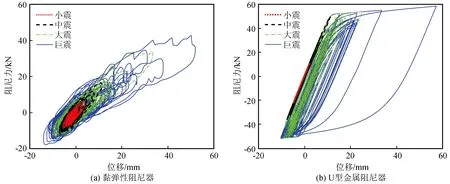
图10 单个阻尼器在DLT352地震动下的耗能情况Fig.10 Energy dissipation of single damper under DLT352 ground motion
如图11所示,为不同强度地震作用下的两种原型结构中所有阻尼器在44条地震动作用下的耗能面积总和的统计情况,图中实线为中位值,虚线为具有84%保证率的值。可见,小震下黏弹性阻尼器的耗能面积明显大于U型金属阻尼器的耗能面积,这与前述单个阻尼器的耗能情况一致。U型金属阻尼器从中震开始耗能,随着地震动强度的增大,其耗能面积逐渐超越黏弹性阻尼器且离散性更大。因此,在地震动强度较小时,如小震或中震,黏弹性阻尼器的耗能效果明显,而地震动强度较大时,U型金属阻尼器的耗能效果会优于黏弹性阻尼器。

图11 阻尼器耗能总和Fig.11 Energy dissipation of all dampers
4 结论
(1) 黏弹性阻尼器在小震下即可发挥耗能作用,附加黏弹性阻尼器的自复位墙结构在小震下的层间位移角和楼层加速度响应比附加U型金属阻尼器的结构小15%~20%,这为控制自复位墙结构在小震下的位移和加速度响应提供了有效方法。同时,U型金属阻尼器在中震下开始屈服,附加U型金属阻尼器的自复位墙结构在大震下的减震效果明显提升,在巨震下的层间位移角相比附加黏弹性阻尼器的结构约减小20%。
(2) 黏弹性阻尼器和U型金属阻尼器对于控制自复位墙结构的地震响应各有优势。为优化自复位墙结构在不同水准地震作用下的抗震性能,建议结合阻尼器自身的特点,通过合理的设计进一步提高自复位墙结构的抗震性能。

