基于土弹簧的桩-土-输电塔抗震性能研究

田 利, 刘凯悦, 刘俊才, 孟祥瑞

(山东大学 土建与水利学院, 山东 济南 250061)

0 引言

输电铁塔作为架空输电线路的关键支撑结构,其承载力性能直接影响输电网络的稳定运行。输电线路不可避免途经烈度较高的地震活动区,地震动激励下导致输电塔在正常使用周期内的失效事件时有发生,例如:1975年海城地震,地震导致了场地液化、基础不均匀沉降,造成100余万米供电线路破坏[1];1999年集集地震,造成输电塔的基础部分产生位移,导致30座变电站停运、高压输电线塔毁损, 甚至全岛停电[2];2008年汶川地震,因地形变化巨大,电力设施基础破坏严重,导致近200条输电线路和16座变电站被严重损毁[3]。由此可见,地震发生时,因基础破坏导致输电塔损坏倒塌事件常有发生。因此,为了保障供电系统安全稳定运行,开展考虑SSI的输电塔性能研究十分必要。

目前输电塔设计中通常在其底部采用固定约束,而忽略了基础对输电塔抗震性能的影响,高估了输电塔的承载能力[4]。为了总结考虑土-结构互相作用时输电塔地震响应的变化规律,目前国内外开展了部分相关研究。徐静等[5-6]建立了考虑土-结构作用的输电塔模型,基于耦合模型开展了地震动激励下输电塔响应分析,并与不考虑基础与结构互相作用的模型开展对比,结果显示场地对不同基础条件下输电塔的结构动力响应影响显著,其中使输电塔地震响应增大的场地条件是软土和中软土。李宏男等[7]基于附加质量法对输电塔的导地线和基础部分的桩体进行等效简化,通过开展非线性动力时程分析验证了简化桩-土-塔-线体系模型的合理性。毛龙[8]对桩-土-输电塔耦合模型进行数值分析,研究了模拟地震动作用下不同场地条件对输电塔动力响应的影响趋势,结果表明中软场地会对耦合模型中的输电塔产生不利影响,且横隔的数目和基础中桩体的长度对输电塔的抗震能力有一定的影响。田利等[9]创建了不同类型场地下同时考虑基础和输电塔的桩-土-结构精细化输电塔-线体系模型,总结了地震激励下考虑和未考虑SSI的数值模型中输电塔结构的薄弱位置,并提出了为输电塔抗震设计提供参考的放大系数。Tamari等[10]研究发现,在场地条件明显不同的输电塔基础上,输电线路会表现出不同的地震反应,并可能引起电缆之间的接触。魏文辉等[11]基于谱比法生成水平-摇摆耦合多维地震动水平分量,研究了耦合多维地震动下考虑基础与输电塔互相作用下塔-线体系响应的变化规律,明确了场地条件为软土时,在其抗震设计中应当考虑场地效应的影响。可以看出,目前已基于有限元软件开展了一系列考虑土-结构相互作用影响下输电塔和塔-线体系的动力响应方面的研究,但对考虑SSI输电塔的倒塌破坏和倒塌易损性方面的研究鲜有涉及,这是由于土体单元多采用实体单元模拟,分析计算时间较长且不易收敛所致。

基于此,本文选取某1 000 kV双回路输电塔为研究对象,建立了考虑和未考虑SSI的输电塔有限元模型,重点分析了SSI对输电塔动力特性、动力响应、倒塌过程和倒塌易损性的影响,探究了SSI对输电塔抗震性能的影响规律。

1有限元模型建立

1.1 工程概况

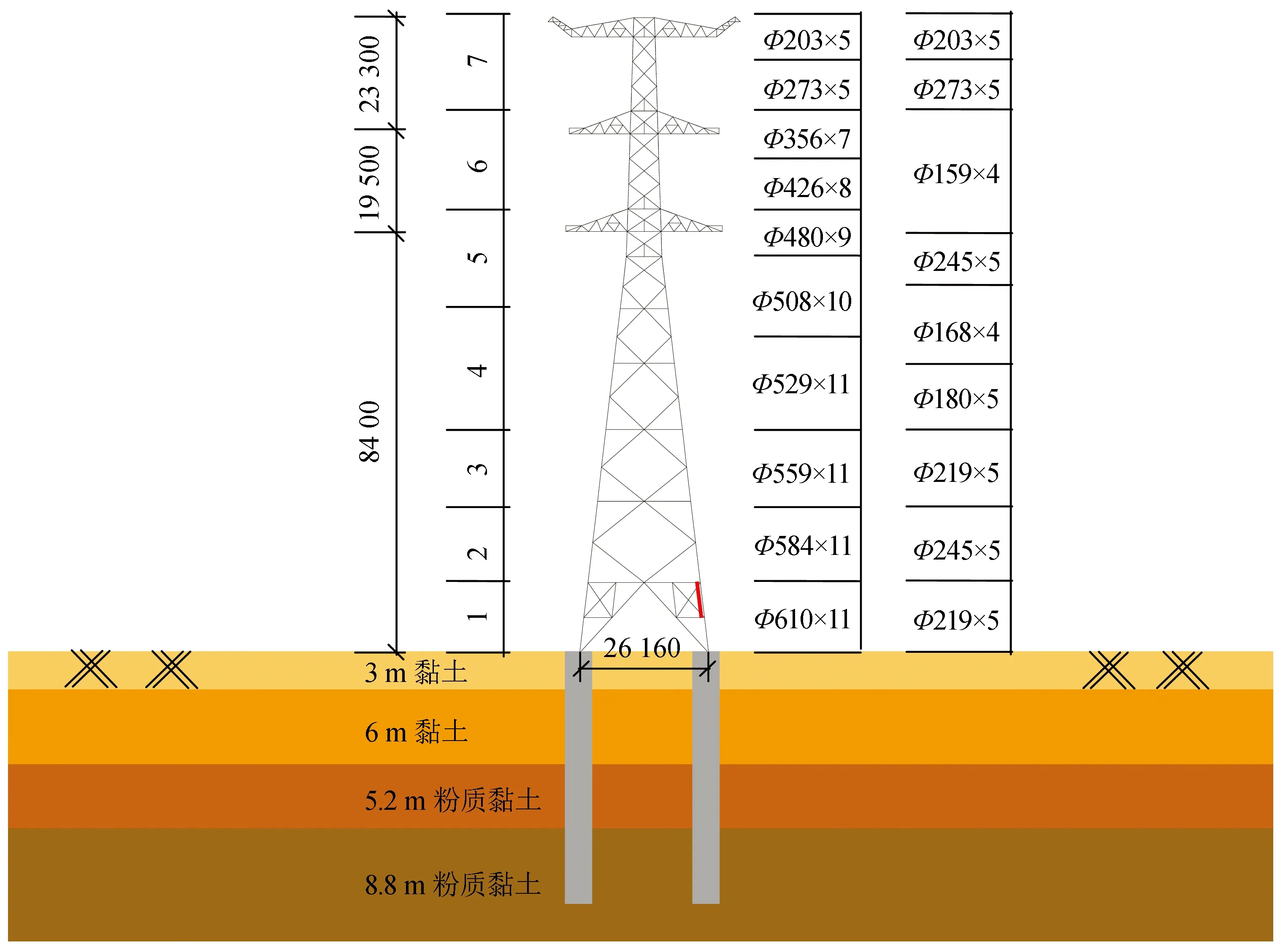
图1 桩-土-输电塔参数(单位：mm)Fig.1 Parameters of pile-soil-transmission tower (Unit:mm)

表1 土体参数

1.2 桩-土-输电塔有限元模型

基于ABAQUS,建立未考虑和考虑SSI的输电塔数值模型,分别为模型Ⅰ和模型Ⅱ,如图2所示。定义垂直塔线方向、顺塔线方向和竖直方向分别为模型的X、Y和Z向。输电塔杆件均采用梁单元建模,输电塔模型包含1 274个单元和463个节点,并且将法兰、螺栓和节点板等构件的质量以集中质量点的形式施加于有限元模型的节点上。模型Ⅰ输电塔直接将塔腿固定在地面上;模型Ⅱ的输电塔底部设有独立桩基础,输电塔塔腿与桩体顶部设置绑定约束,桩体底部仅限制转动方向的自由度。为了提高计算效率,将钢筋混凝土桩等效为单一材料的桩体,等效前后桩体的刚度保持不变,等效计算时材料参数均采用标准值。等效简化后的桩体使用梁单元B31创建,桩体与土体间的相互作用则采用零长度弹簧模拟[12-13]。在进行有限元建模时,将长度为20 m的桩体分成10个等距2 m的桩单元,从而定

图2 输电塔有限元模型Fig.2 Finite element model of transmission tower

义了11个桩节点,每个桩节点处均设置沿X、Y和Z的零长度弹簧,零长度弹簧的形式和位置如图3所示。根据表1中不同土层信息,确定零长度弹簧X、Y和Z三个方向的具体参数。

1.3 弹簧刚度确定

零长度弹簧刚度的具体参数是依据相关规范[16-17]确定的,其中,水平方向的零长度弹簧刚度可通过p-y曲线确定。通过规范计算的p-y曲线是与深度相关的土反力与水平变形的关系曲线,将土体的非线性特征、土层位置及外荷载类型进行了综合考虑,能够真实地模拟桩基础的实际受力状态,对桩基础的非线性分析具有良好的适用性。

当Z>ZR时,p-y关系曲线如下:

(1)

当Z≤ZR时,p-y关系曲线如下:

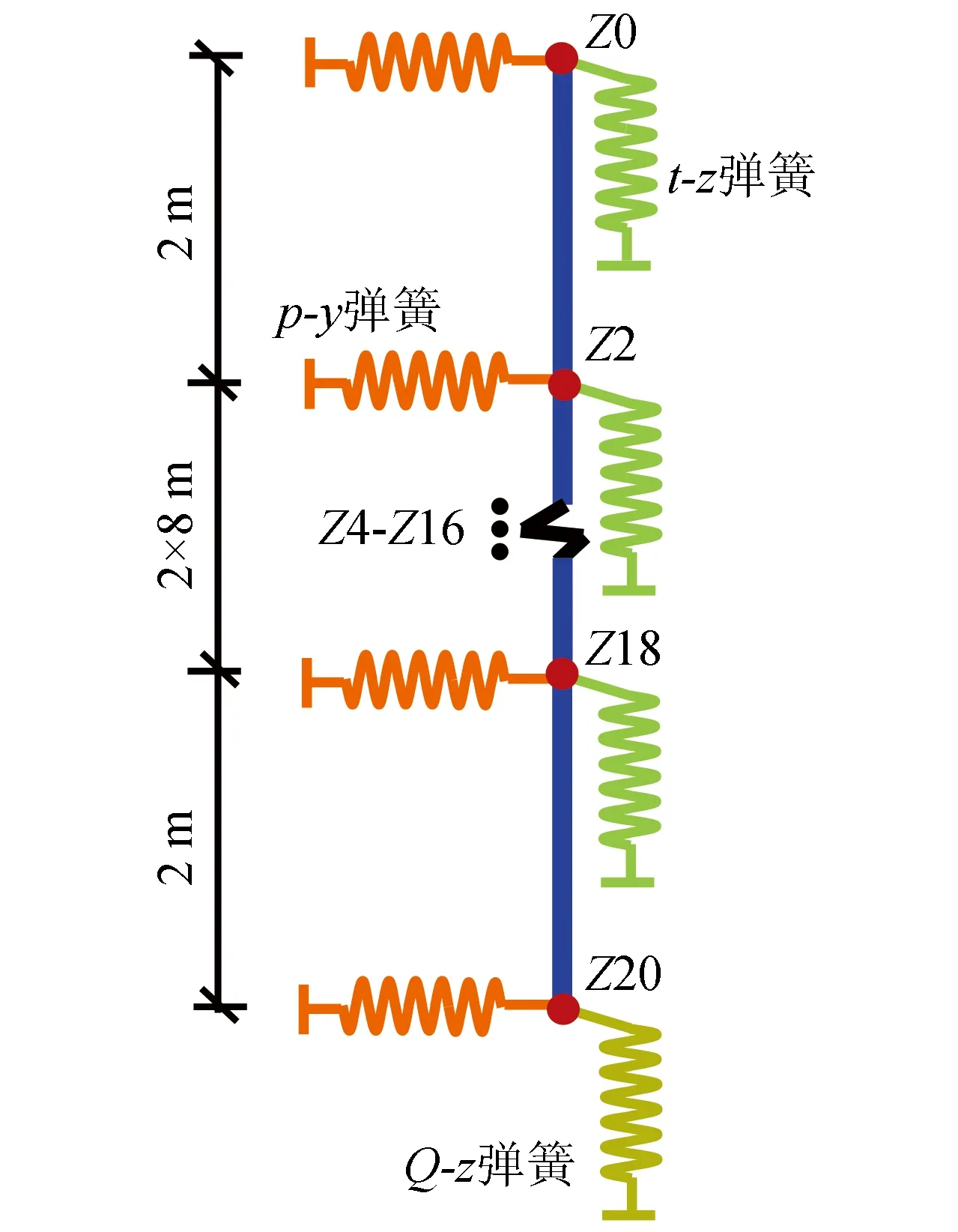
图3 弹簧布置示意图Fig.3 Schematic diagram of spring arrangement

(2)

式中:p为地面下某一深度处的土体水平反力;y为地面下某一深度处的侧移;pu为极限土抗力,由式(3)计算;yc为极限土抗力一半处的挠度,由式(4)计算;Z为某点处的地面以下深度;ZR为土面以下到抗力减少区域底部的深度,由式(5)计算。

(3)

yc=2.5ε50D

(4)

ZR=6suD/(γ′D+Jsu)

(5)

式中:su为未扰动黏土土样的不排水抗剪强度;γ′为土体有效重度;D为桩的直径;J为无量纲常数(取0.5);ε50为实验室进行未扰动土样不排水压缩试验时,出现 1/2 最大应力时的应变。

竖直方向的零长度弹簧模拟桩身摩阻力和桩端阻力,桩身摩阻力通过在Z0-18桩节点处沿Z方向设置竖向弹簧模拟,其具体弹簧参数可以由t-z曲线确定,桩端阻力通过在Z20桩节点处沿Z方向设置竖向弹簧模拟,其具体弹簧参数可以由Q-z曲线确定,如图4所示。由于t-z曲线和Q-z曲线与p-y曲线的计算过程相似,故本文不再介绍其计算过程,具体可以参考API规范[16]。

图4 弹簧刚度曲线Fig.4 Spring stiffness curves

2 动力特性分析

输电塔是一种高耸且强柔性的结构,阻尼对其动力特性和地震动激励下的响应均有显著的影响。模型Ⅰ仅考虑输电塔阻尼中的结构阻尼;模型Ⅱ同时设置输电塔结构阻尼和土壤阻尼。其中输电塔的结构阻尼比假定为2%[18],土壤的阻尼比假定为5%[19-20]。

为定量研究SSI在动力特性方面对输电塔的影响,对模型Ⅰ和模型Ⅱ中输电塔分别开展特征值分析。模型Ⅰ和模型Ⅱ中输电塔X、Y和Z方向的前两阶振动频率及其对比结果如表2所列。可以看出,在前六阶频率中,模型Ⅰ中输电塔的频率均大于模型Ⅱ的,差异主要表现在绕X和Y方向振型上,最大差异达24%。因此,SSI会减小输电塔的自振频率[21],这是由于考虑SSI会减小耦合模型的整体刚度。

表2 输电塔动力特性

模型Ⅰ和模型Ⅱ的前三阶输电塔振型分别如图5和图6所示,从图中可以看出,模型Ⅰ和模型Ⅱ中输电塔均首先出现X和Y方向的整体弯曲振型,接着出现绕Z向的整体扭转振型,振型形状基本相同。因此,考虑SSI对输电塔振型形状影响不大。

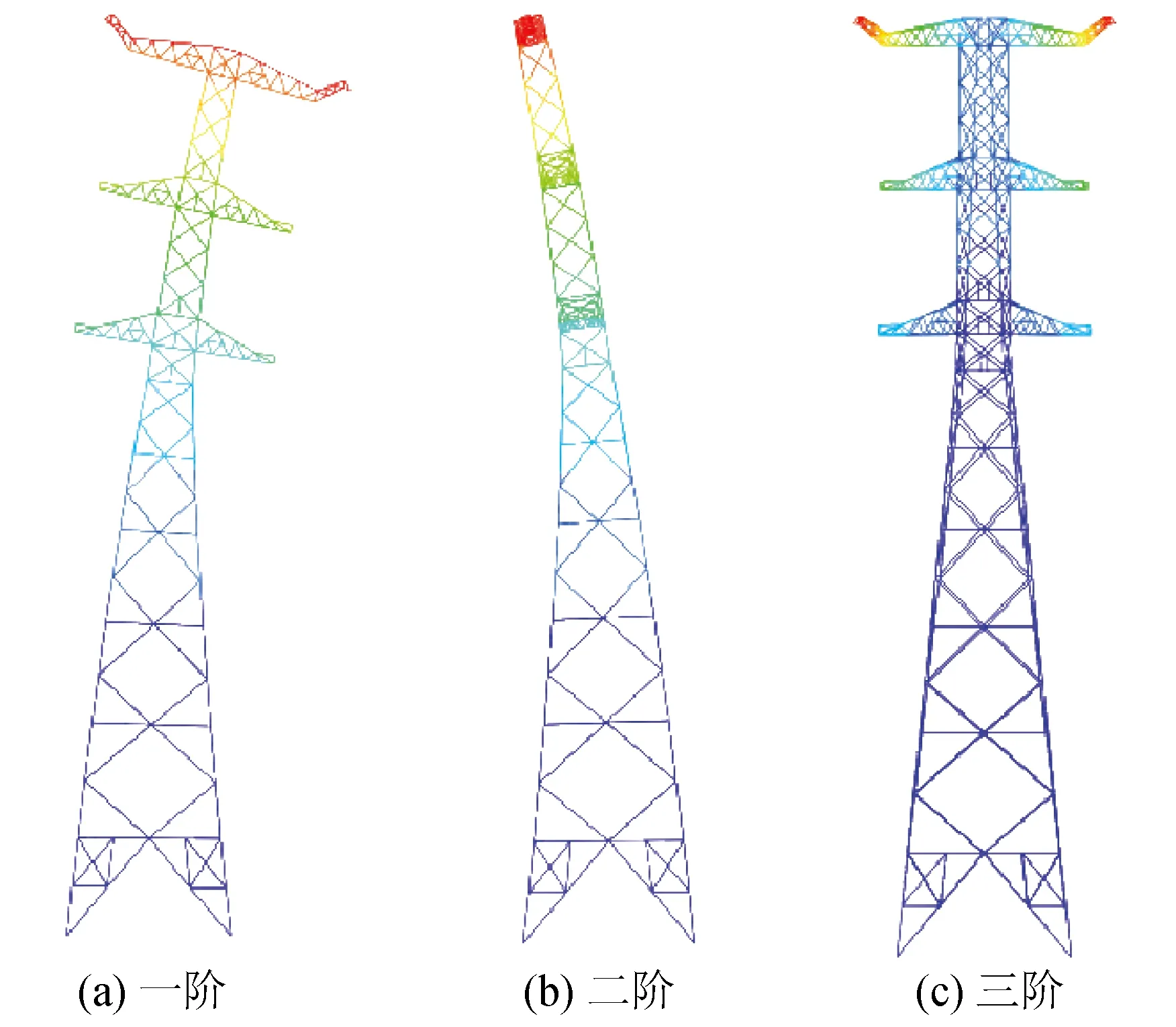
图5 模型Ⅰ振型图Fig.5 Vibration mode diagram of model Ⅰ

3 考虑SSI的输电塔地震响应分析

基于有限元模型开展的非线性动力分析,整个非线性动力分析分为前后两个分析步,在第一个分析步中,模拟对输电塔施加自重的过程并在后续的分析步中保持自重不变;在第二个分析步中,将地震动记录施加到模型Ⅰ中输电塔底部和模型Ⅱ中桩体底部。通过分析不同模型中输电塔的振动响应,研究SSI对输电塔地震响应的影响规律。

图6 模型Ⅱ振型图Fig.6 Vibration mode diagram of model Ⅱ

3.1 地震动选取

在太平洋地震工程中心的地震动数据库中下载10条地震动记录,表3列出了选取的地震动的详细信息,包括地震名称、震级大小、年份和台站。目前的输电塔抗震设计通常基于弹性理论,即保证在输电塔所处地区的多遇地震下输电塔中杆件不发生屈服或屈曲。本节目的是研究SSI对输电塔地震响应的影响,在非线性动力时程分析中考虑杆件屈服或屈曲将显著影响计算时长,因此,将表3中地震动中较大分量的地面峰值加速度(Peak Ground Acceleration,PGA)调整到0.2g,其余方向按照相同比例进行调整。地震动输入时,10条地震动加速度时程的较大水平分量沿输电塔纵向(Y向)输入,另一水平分量沿输电塔横向(X向)输入[22]。

表3 选取的地震动

3.2 地震响应分析

将输电塔沿高度方向自下而上划分7个节间(如图1所示),提取不同地震动下模型Ⅰ和Ⅱ中输电塔各节间处的峰值位移、加速度和杆件应力响应,并将10条地震动下的位移、加速度和应力等响应进行平均,结果如图7所示,进而评估SSI对输电塔在地震响应方面的影响规律。以位移响应为例,如图7(a)示,不同地震动激励下输电塔的振动响应存在较大区别;随高度增加,不同节间顶部的位移峰值逐渐增大,在塔顶处达到峰值,且不同高度处模型Ⅱ中输电塔的平均位移峰值均大于模型Ⅰ的。由此可知,考虑SSI能够显著增大输电塔的地震响应,且在研究地震动激励下输电塔动力响应时应当充分考虑不同地震动对结构的影响。

图7 输电塔沿高度的动力响应对比Fig.7 Comparison between seismic responses of transmission tower along the height

4 输电塔的倒塌易损性研究

采用Tian-Ma-Qu材料本构[14-15],定义模型Ⅰ和模型Ⅱ中输电塔材料,开展IDA分析,研究SSI对输电塔倒塌过程和易损性的影响。通过开展不同地震动激励下考虑和不考虑土-结构相互作用的输电塔的IDA分析,获得两种模型的IDA曲线簇,总结SSI对结构倒塌PGA的影响规律,分析输电塔塔顶位移,明确输电塔破坏机理和倒塌过程,并对比不同模型的易损性曲线,研究SSI对输电塔易损性的影响。

4.1 倒塌破坏分析

部分IDA曲线簇如图8所示,当PGA在一定范围内时,输电塔塔顶位移随PGA的变化而线性变化,但达到倒塌PGA时,输电塔顶部位移突然增大,这是因为输电塔的损伤累积到一定程度,输电塔产生动力失稳,出现倒塌。由于地震动的不确定性,输电塔倒塌PGA差距较大,在不同地震动激励下,模型Ⅰ中输电塔倒塌PGA的范围为0.75g～1.48g,模型Ⅱ为0.62g～1.35g,显然模型Ⅱ中输电塔的倒塌PGA小于模型Ⅰ的,且输电塔发生倒塌破坏时,考虑SSI的输电塔塔顶平均位移明显小于不考虑SSI的。

图8 不同地震动作用下输电塔X方向IDA曲线簇Fig.8 IDA curve cluster of transmission tower in the X directionn under different ground motions

图9给出了模型Ⅰ中输电塔在PGA=0.74g的GM01地震动作用下的塔顶位移时程曲线和模型Ⅱ中输电塔在PGA=0.65g的GM01地震动作用下的塔顶位移时程曲线,以模型Ⅱ为例,当t1=19.3 s时,输电塔顶部位移最大,塔身位移非常小,当t2=24.7 s时,输电塔塔身发生较大位移,位移时程曲线出现发散的现象;当t3=26.5 s时,输电塔塔身发生十分明显变形,位移时程曲线发散明显,输电塔发生整体倒塌破坏。而模型Ⅰ和模型Ⅱ中输电塔的倒塌过程和倒塌破坏形状相似,因此考虑SSI不会改变输电塔的倒塌破坏形式。

图9 倒塌PGA作用下输电塔塔顶位移时程曲线Fig.9 Time history curve of top displacement of transmission tower under the action of collapsed PGA

4.2 易损性分析

易损性可定义为在给定地震强度下,结构地震需求达到或超过其规定的承载力的条件概率,可由易损性曲线表示。通常认为地震强度指标服从对数正态分布[23],本文选用塔顶水平位移作为地震强度指标与结构地震需求,则结构倒塌易损性的数学描述如下:

(6)

(7)

(8)

式中:n为地震动记录数量;PGAi为给定地震动激励下结构发生倒塌时其PGA值。

根据上述易损性公式,计算出不同模型的结构倒塌易损性曲线如图10所示。从图中可以看出,模型Ⅰ和II中输电塔的倒塌易损性曲线差异明显,相同PGA地震动作用下,模型Ⅱ中输电塔倒塌概率均高于模型Ⅰ中输电塔倒塌概率,当输电塔倒塌概率为50%时,模型Ⅰ和II对应地震动PGA分别为1.05g和0.91g。因此,考虑SSI会使输电塔结构发生倒塌的概率增大,抗倒塌能力降低。

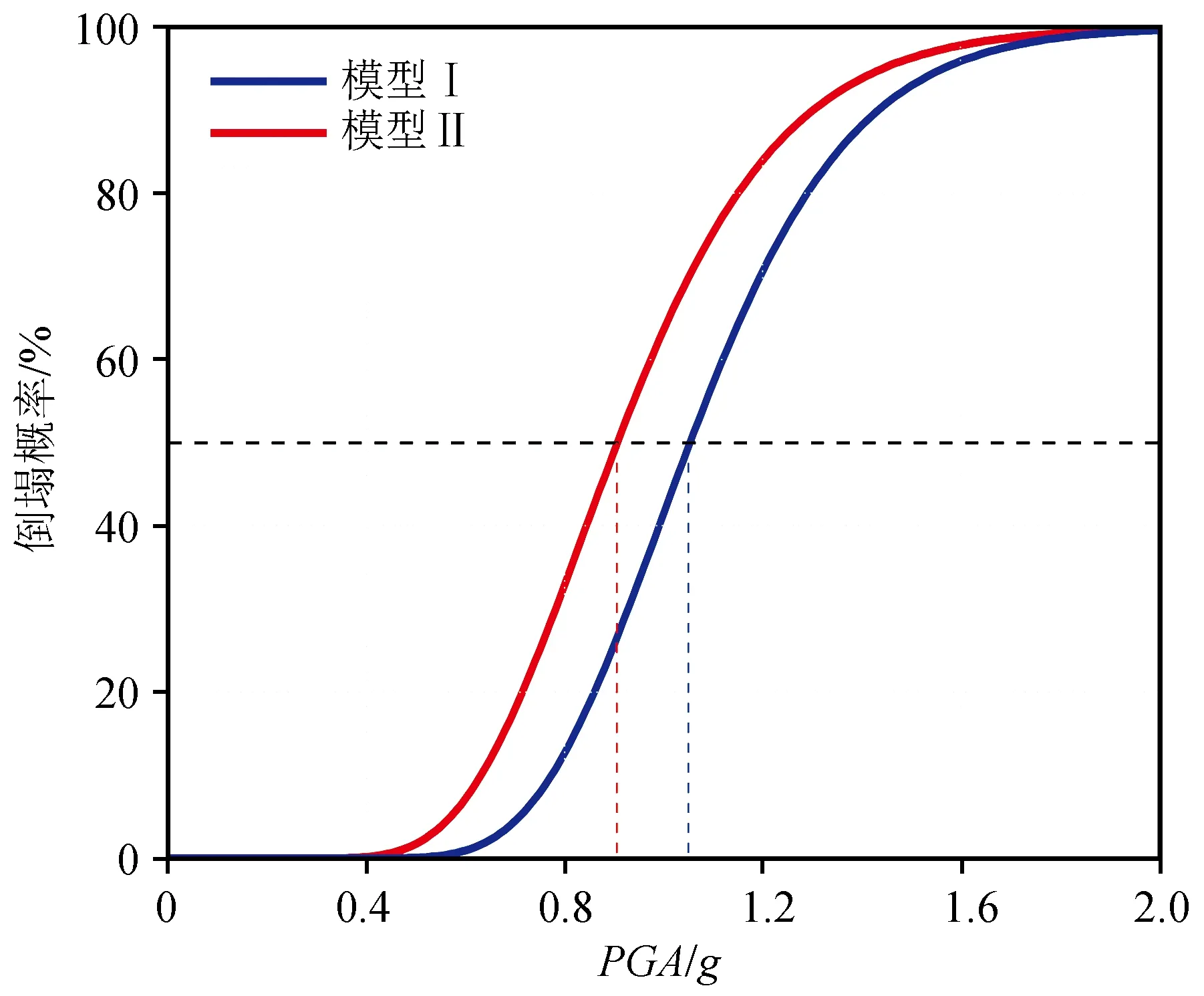
图10 输电塔倒塌易损性曲线Fig.10 Collapse vulnerability curves of transmission tower

5 结论

本文对考虑SSI的输电塔的地震响应和破坏机理进行了综合数值模拟。选取某1 000 kV输送电线路工程中一基直线塔为研究对象,在ABAQUS中创建未考虑和考虑SSI的输电塔有限元模型,基于有限元模型,开展动力特性分析,研究SSI作用下输电塔的振动响应、倒塌破坏和易损性,明确SSI对输电塔结构抗震性能的影响。通过以上研究,主要得出以下结论:

(1) 基于p-y曲线,在桩体的不同节点处设置零长度弹簧可以有效模拟桩-土相互作用,该模拟方法能够提高桩-土-输电塔耦合模型的计算效率和简化建模过程,为开展考虑SSI对输电塔抗震能力的影响研究奠定基础。

(2) 考虑SSI未使输电塔的振型发生改变,但通过改变不同振型的振动频率显著影响其动力特性,考虑SSI输电塔的自振频率均小于未考虑SSI输电塔的自振频率,最大差异达24%。

(3) 考虑SSI的输电塔沿高度方向的地震响应均明显大于未考虑的,这说明目前规范设计对于输电塔抗震是不利的。

(4) 考虑SSI的输电塔薄弱位置和倒塌模式与未考虑SSI的是一致的,但考虑SSI的输电塔倒塌PGA减小,输电塔失效概率增加。