柴油机曲轴疲劳计算中曲线数据提取与拟合
田中旭,赵娟,李奇彦,王川,侯璋天
(上海海洋大学 工程学院,上海 201306)
0 引言
曲轴是柴油机系统中最为核心的运动部件之一,曲轴的运动可靠性取决于曲轴的疲劳强度特性,进行船用柴油机曲轴疲劳强度校核时,大多数计算参数都采用图片方式呈现,如弯曲应力集中系数、扭转应力集中系数、结构细节的影响系数等,因此,为船级社数据的后期分析处理带来了很多不便之处[1]。运用图像处理技术,结合岭回归、lasso回归等曲线拟合方法,构建能反映计算参数性质的经验公式,对于研究曲轴疲劳强度计算软件开发是非常重要的。
目前,对于复杂曲线数据提取问题,文献[2]从打印的图形中提取曲线数据的方法,采用区域插值的方法来去除曲线中的一些间断点,但是提取出的曲线仅有一条。文献[3]对于电磁兼容图片测试曲线中的数据提取,建立一种关于像素坐标和坐标轴的分布的数学关系,遍历扫描图片坐标轴内有效区域的每一个像素点,从而实现数据的提取,但是此方法提到曲线提取对于数据量大的复杂曲线,其不能很好实现精准提取。文献[4]提出了一种针对两条曲线的识别提取算法和一种针对多条彩色曲线的识别提取算法,针对不同曲线运用插值法,但是提取出的数据精度不高。文献[5]、文献[6]主要利用Hough变换,研究了有曲线方程的圆、椭圆曲线的识别,而对于曲线方程未知的一般性非参数平面曲线,其识别与提取就无法实现了。
本文考虑图像干扰多,多曲线等因素,根据曲线本身的特性,提出了一种曲线数据提取的方法,利用像素点的位置关系对曲线图片进行数据遍历扫描,避免繁琐的操作,获取初步的曲线数据表,然后通过比较多种数据拟合方法,选择最大拟合优度的回归算法得出拟合经验公式,再做误差分析,符合标准提取出曲线数据。
1 曲线图像降噪
曲轴疲劳强度计算参数表是以图片形式呈现的,可能包含一些背景网格和水印,这些都会对图片造成干扰。所以,为方便人工取点与降低干扰,先对图1进行图像降噪。

图1 特征原始图
本文所采用的是像素值法,即根据该点的像素值,为此来判断该点是否为曲线上的有效点,再将图片转化为只有黑白两色的灰度图有助于像素点数值的迅速判别[3]。处理的关键是通过阈值来判断,f(ek,ω)曲线灰度图的主要构成是背景色和曲线两种颜色,而且呈现出的图像两部分的差别非常大,将部分目标错判成背景或者将部分背景错分成目标都会导致两部分差别变小,为此本文采用大津法来进行处理[7]。再利用深度学习对原始图像进行去除复杂图像水印和内部的网格线,需要先通过对大量训练图片样本测试,保留曲线部分以及坐标轴的边界线,再通过高斯滤波消除噪音,为了更好的平滑图像质量,使用高斯滤波器与图片进行卷积,以此来减少边缘检测器上面明显的噪声影响。高斯滤波的计算满足式(1):
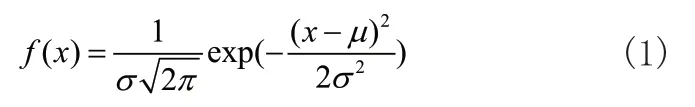
通过高斯滤波器降噪后的图2为方便后续数据处理。
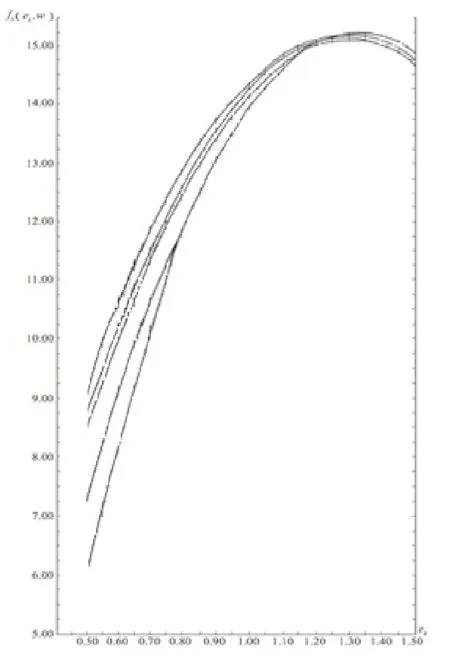
图2 待提取数据的曲线
2 曲线数据提取
为了将复杂曲线分离,提取图形数据,先让该图像显示最大化,便于取点。这里取到的坐标是像素坐标,将像素坐标值存放在数组xp,yp中,将取得的点像素坐标依据坐标轴的像素坐标进行转换,得到曲线上点的真实坐标。再将真实坐标存放在数组xc,yc,中。其中像素坐标与真实坐标的转换满足式(2)和式(3):

取点后,再通过公式将像素坐标与实际坐标进行转换后,提取出ω=0.38、ω=0.36、ω=0.25的部分坐标值如表1所示。

表1 曲线上提取的数据点
3 多曲线数据拟合
曲线拟合是指根据获取的部分数据点的数据集,构造一个新的函数解析式,使其部分数据点尽可能接近拟合出的值。
3.1 多曲线拟合原理分析
目前,常用的拟合方法有二次函数拟合、抛物线拟合、指数式拟合等,根据曲线线条样式,该曲线采用高次幂数据拟合。首先建立数学模型:
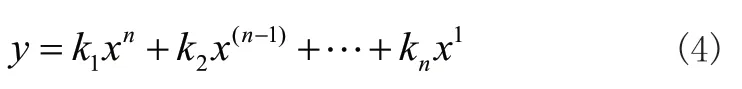
则根据高次幂数据拟合原理有:

令k1,k2,...,kn合理取值,使得M的取值最小。则满足式(5)的函数f(x),求高次幂拟合曲线的解。
函数类型的选取决定拟合优度,只有选取合适的函数类型,才能得到合适的拟合曲线。常用的函数有多项式函数、幂函数、傅立叶函数、高斯函数等。本文以多项式高次幂函数为力对曲线进行拟合。高次幂多项式拟合公式为:
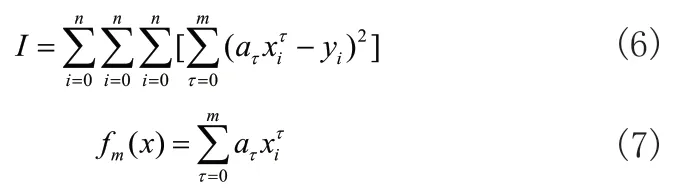
满足式(7)的fm(x)就是高次幂的拟合多项式。公式中的α0,α1,...,αm的多项式系数,根据多项式极值存在的必要条件,可求得:
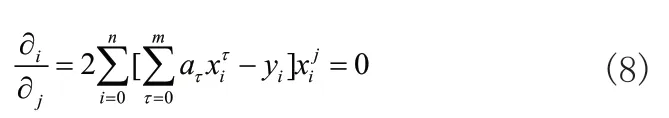
式(8)中,j=0,1,…,m。
将式(9)转换成矩阵的形式:

可以证明式(9)的系数矩阵是一个对称正定矩阵,所以存在唯一解。根据上式可以求解得到多项式系数矩阵。
此时,高次幂数据拟合完成,取ω=0.35这个数值的数据,得到拟合曲线计算数据与真实数据之间的差值如图3所示。
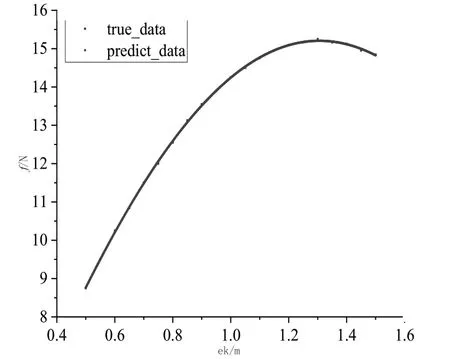
图3 曲线计算数据多元图
3.2 多曲线拟合方法选择
曲线数据拟合的方法有很多,以下针对四种拟合方法普通最小二乘法[6]、多项式回归[7]、岭回归[8](ridge regression)、Lasso回归[9]进行比较分析。普通最小二乘法又称高斯法,通过N个不同的数据点拟合出我们设定函数的未知参数的过程。多项式回归将会对连续性的数据做出预测,从数据里求出回归方程。岭回归(ridge regression)是加了二阶正则项的最小二乘,岭回归用于处理变量间存在共线性。Lasso回归是通过拉格朗日乘数法原理,拟合出回归曲线,对于参数w增加一个限定条件,能到达和岭回归一样的效果。如图4所示为各算法对拟合优度的影响曲线。

图4 各算法拟合优度影响曲线
此时,各算法拟合优度的比较,取多项式回归是最理想化的拟合方法,它得到的拟合曲线优度最接近1,说明此方法拟合的曲线是最接近目标曲线。
3.3 多项式拟合次幂选择
多项式曲线拟合回归模型有一次拟合、二次多项式拟合、三次多项式拟合、四次多项式拟合,在实验过程中,要根据不同次幂拟合优度和均方误差等方法进行比较,选择最适合曲线拟合模型次数,才能得到最合理的经验公式。图5为各次幂对拟合优度的影响,图6为各次幂对绝对值误差的影响,图7为各次幂对均方误差(MSE)的影响。
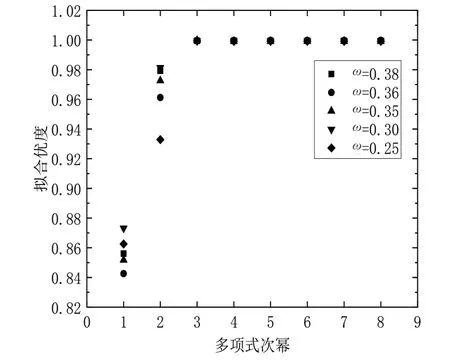
图5 各次幂对拟合优度的影响

图6 各次幂对绝对值误差的影响

图7 各次幂对均方误差(MSE)的影响
拟合优度R2的值约接近1,说明回归直线对预测值的拟合程度越好,反之,R2的值越小,说明拟合程度越差,图5当多项式拟合次数达到四次时,拟合优度几乎接近1,就是最满意的拟合程度。绝对值误差(MAE)用来评估回归模型,图6的绝对值误差都接近1,说明改变次数对改变绝对值误差的影响不大。均方误差(MSE)是指参数估计值与真实值之差平方的期望值,MSE是评价数据变化程度较方便的方法,图7的MSE值越小,说明预测模型描述拟合数据具有更好的精确度,由图知四次幂拟合具有更好的精度。以上回归模型的评估指标得出拟合的经验公式如式(10)所示:
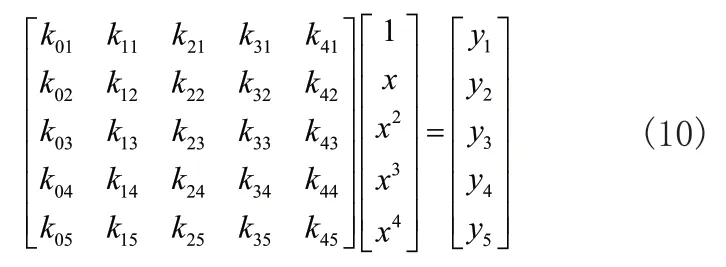
式(10)中的n=4时满足评估指标最优化,根据多项式极值存在的必要条件,可求得式(11)的经验公式系数矩阵值:

3.4 曲线拟合误差分析
上述方法只是对图像中的数据进行了提取,并不能说明此方法的准确性,为了说明该提取数据方法的准确性,要对提取出的结果进行误差分析。
曲线数据可以根据曲线经验公式得到的,现在根据误差分析公式,通过拟合所得到的数据与原始数据进行对比来获得误差的大小。误差的计算公式为:

求得与原始提取数据的误差率分别如表2所示。
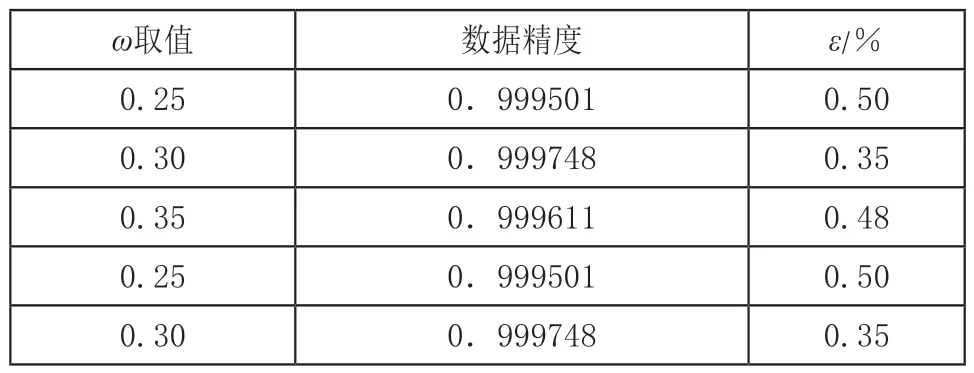
表2 曲线误差分析数据表
柴油机疲劳强度分析过程中,校核强度过程中需要对参数进行查表,五条拟合曲线的误差率都在误差范围之内,说明此方法拟合曲线数据满足柴油机查表数据要求。根据得到的经验公式得到相应的数据集,再通过数据集开发查表分析软件,可以直接通过输入数值得到查表后的参数值,节省了查表的人力和时间,使得操作更方便。
4 结语
通过检测系统的运行,表明柴油机曲轴疲劳计算曲线数据提取与拟合方法研究,具有结果稳定、准确的优点,适用于柴油机疲劳强度分析过程中计算参数的查找,同时该高次幂曲线拟合效果明显,实现了自动、快速查找系数,具有较高的研究价值。对于类似的曲线提取,可以对不清晰,干扰大的图像先进行图像预处理,可以通过高斯滤波、二值化、阈值化等方法初步去除噪声等干扰。确定图像中坐标轴位置与坐标刻度,使图像中的像素坐标转换为真实坐标。在曲线上进行取点,对于取到的坐标点进行多种方法曲线数据拟合,分析比较拟合优度和均方误差,找到一条拟合优度最接近1的拟合方法,求解拟合经验公式。通过本方法得到的曲线与原始曲线相比,数据非常吻合,误差也相对较小。
——拟合优度检验与SAS实现

