解析几何中的最值问题
廖永福
(福建省厦门第二中学 361009)
解析几何中的最值问题涉及的知识面较广,综合性较强,因而常以中档题或压轴题的形式出现.解决这类问题的常用方法有代数法、几何法和三角法等.
1 代数法
代数法就是将题目中某些变化的几何量(如斜率、坐标等)设为自变量,并用它表示目标变量(如弦长、距离、周长、面积等),即建立目标函数,然后应用函数或不等式等知识解决问题的一种方法.应用代数法重在运算,要做到运算准确,还要注意函数的定义域,否则容易出错.
例1(2021年北京卷9)已知圆C:x2+y2=4,直线l:y=kx+m,若当k的值发生变化时,直线被圆C所截的弦长的最小值为2,则m的取值为( ).
分析先求得圆心到直线的距离,即可表示出弦长,再根据弦长的最小值求出m.
解析由已知得圆心为(0,0),半径为2.
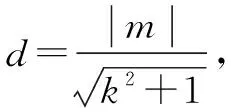
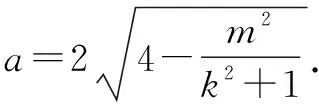
当k=0时,弦长取最小值2,即
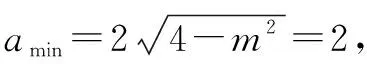
故选C.
点评本题主要考查直线与圆的位置关系,点到直线的距离公式和简单函数的性质等,体现了直观想象、逻辑推理和数学运算等核心素养,解题关键是利用勾股定理将弦长表示成斜率的函数,再利用函数的性质求解,属于基础题.
例2(2017年全国Ⅰ卷理10)已知F为抛物线C:y2=4x的焦点,过点F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为( ).
A.16 B.14 C.12 D.10
分析先写出|AB|,|DE|的表达式,再利用基本不等式求出|AB|+|DE|的最小值.

故直线l1,l2的方程分别为

k2x2-(2k2+4)x+k2=0.


同理可得|DE|=4k2+4.
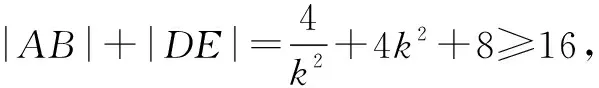
点评本题主要考查直线与抛物线的位置关系,弦长公式和基本不等式等,体现了直观想象、逻辑推理和数学运算等核心素养,解题关键是将|AB|+|DE|表示成直线l1的斜率的函数,再用基本不等式求解,属于中档题.
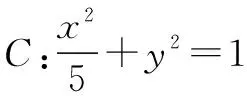
2 几何法
几何法就是充分挖掘题目中隐含的几何意义与几何特征,应用圆锥曲线的定义或平面几何的知识解决问题的一种方法.应用几何法重在推理,要做到思维严谨,步步有据.

分析根据双曲线的定义等价转化|PF|,分析何时△APF的周长最小,然后用间接法计算S△APF.
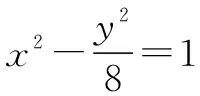
故F(3,0),F′(-3,0).
当点P在双曲线左支上运动时,由双曲线定义知|PF|-|PF′|=2.
所以|PF|=|PF′|+2.
从而△APF的周长=|PA|+|PF|+|AF|=|PA|+|PF′|+2+|AF|.


图1

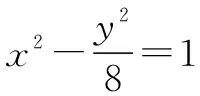

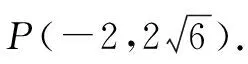

点评本题主要考查双曲线的标准方程及其几何性质,考查三角形的周长和面积等,体现了直观想象、逻辑推理和数学运算等核心素养,解题关键是根据双曲线的定义等价转化|PF|,找到△APF的周长取最小值时点P的位置,属于中档题.



化简,得2x2-mx+4=0.

点评本题主要考查直线与曲线的位置关系,点到直线的距离和平行线间的距离等,体现了直观想象、逻辑推理和数学运算等核心素养,解题关键是将动点到定直线的距离问题转化为两条平行直线间的距离,属于中档题.
变式练习2(2020年全国Ⅰ卷理11)已知⊙M:x2+y2-2x-2y-2=0,直线l:2x+y+2=0,P为l上的动点,过点P作⊙M的切线PA,PB,切点为A,B,当|PM|·|AB|最小时,直线AB的方程为( ).
A.2x-y-1=0 B.2x+y-1=0
C.2x-y+1=0 D.2x+y+1=0
3 三角法

例5(2018年北京卷理7)在平面直角坐标系中,记d为点P(cosθ,sinθ)到直线x-my-2=0的距离,当θ,m变化时,d的最大值为( ).
A.1 B.2 C.3 D.4
分析根据点到直线的距离公式,将d表示成θ和m的函数,再分别把θ和m看作自变量,利用函数的性质求解.
解析由点到直线的距离公式,得
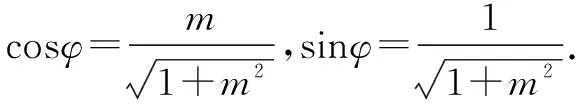

点评本题主要考查点到直线的距离公式,二次函数和三角函数的性质等,体现了逻辑推理和数学运算等核心素养,解题关键是将d表示成θ和m的函数,再利用函数的性质求解,属于中档题.
例6 (2021年全国乙卷理21)已知抛物线C:x2=2py(p>0)的焦点为F,且F与圆M:x2+(y+4)2=1上点的距离的最小值为4.
(1)求p;
(2)若点P在M上,PA,PB是C的两条切线,A,B是切点,求△PAB面积的最大值.
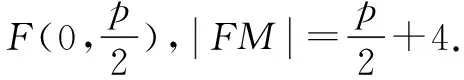

解得p=2.
(2)抛物线C的方程为x2=4y.
因为点P在M上,可设P(cosθ,-4+sinθ),θ∈[0,2π).
由已知,过点P的抛物线C的切线l斜率存在,记作k,则l的方程为
y=k(x-cosθ)-4+sinθ.

x2-4kx+4kcosθ-4sinθ+16=0.
因为l与C相切,所以
△=16k2-4(4kcosθ-4sinθ+16)=0.
即k2-kcosθ+sinθ-4=0,
(*)
且切点为(2k,k2).
设切线PA,PB的斜率分别为k1,k2,则
直线AB的斜率
直线AB的方程为
因为k1,k2是方程(*)的两个根,
所以k1+k2=cosθ,k1k2=-4+sinθ.
所以P(k1+k2,k1k2).
因为点P到直线AB的距离
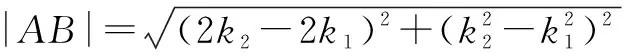
所以△PAB面积



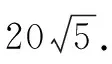
点评本题主要考查圆与抛物线的标准方程和几何性质,直线与抛物线的位置关系以及三角形的面积公式等,体现了直观想象、逻辑推理和数学运算等核心素养,解题关键是引进参数θ,将△PAB的面积表示成θ的函数,属于难题.
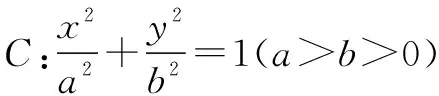
(1)求C的方程;
(2)点N为椭圆上任意一点,求△AMN的面积的最大值.
变式练习答案:

