基于“构造法”的高中数学解题思路探索

庄素慧

(福建省漳州第一中学 363000)

数学是高中学科当中对学生的知识运用以及抽象能力要求最高的一门学科，其本身的学科难度让不少学生望而却步，尤其是一些难题，更是让一些学生毫无头绪.传统的解题思路某种程度上是简单的解题方法，但是面对一些已知条件和所求所证问题之间的联系不明显的时候，会让大多数学生不知所措，这也是其知识运用的僵化体现，数学解题思维的培育就是需要学生打破解题思维的僵化，基于自身的知识经验活学活用，创新思维，这也是构造法的内涵.

1 构造法在高中数学解题中的实际运用

1.1 解题直观化：函数的构造

在高中的数学学习当中函数的重要性不言而喻，更是高考的必考点.而且函数本身就是一种针对未知关系和已知关系的表达，数学历史上很多的著名问题都是借助函数得到论证的.所以，针对高中解题中的构造法的应用，通过构造函数展开题目的分析论证无疑是高效的，通过对已知信息的深化挖掘，从而让复杂的题目内容变得直观、简化，从而提高解题效率和解题精准度，这种构造函数的方法也在几何和代数问题的解决当中得到广泛使用.

例1 已知关于x的方程x2-(2a+1)sin(cosx)+1-4a2=0有唯一实数解，求实数a的值．

分析基于题目我们可以看出这是一道二次元方程题.但是因为含有未知参数，很多学生毫无头绪.但是我们通过认真观察可以发现题目当中的一些已知和未知参数可以用一些函数关系来表达.在教师针对案例讲授时，教师可以分析问题后引导学生书写解题过程，让学生领悟整体的解题思路，分析函数构造法的具体运用方式，让学生做到会一题，通一类，有效提高教师的教学效率和学生的学习效率.

解析构造函数f(x)=x2-(2a+1)sin(cosx)+1-4a2，因为f(-x)=f(x)，所以f(x)为偶函数.

设x0为f(x)=0的解，则-x0也为f(x)=0的解．

由题目已知可得，f(x)=0有唯一的实数解，即-x0=x0，显然x0=0．

所以f(0)=02-(2a+1)sin(cos0)+1-4a2=0.

即(2a+1)(1-2a-sin1)=0.

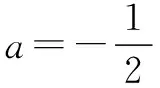
1.2 条件关系的表达：方程的构建

函数和方程的联系性极大，函数的构造可以让题目更直观化，同理，方程的构造也可以极大地简化解题过程.而且当方程和函数同时运用的时候往往可以解决大部分的难题.方程的构造需要建立在对于已知条件的深入分析，将各条件和内容之间的关系理清，从而利用方程构建这种已知关系之间的方程式表达，有效解决问题.

例2 已知a>b>c，且a+b+c=1，a2+b2+c2=1，求a+b的范围.

分析根据已知条件，我们可以通过对问题的结构和数量关系的分析构建等量方程式，从而有效表达已知条件和未知量之间的关系，而且可以通过变形恒等式，实现内容由抽象化转向实质化和特殊化，从而有效提高学生的解题效率，促进学生学科核心素养的提高.

解析由a+b+c=1可得a+b=1-c.

所以(a+b)2=(1-c)2.

将a2+b2+c2=1代入得ab=c2-c.

所以可知a，b是方程x2+(c-1)x+(c2-c)=0的两个不等的实根.

所以Δ=(c-1)2-4(c2-c)=-3c2+2c+1>0.

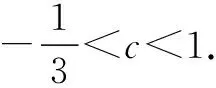
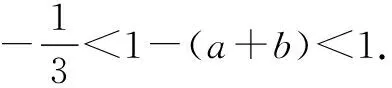
又由(a+b+c)2=1，得

1+2ab+2bc+2ac=1.

所以ab+bc+ac=0.

而a,b,c不可能同号，即c<0.

即a+b=1-c>1.

1.3 解题过程的优化：数列的构造

等差数列和等比数列难度虽然不是很高，但是其中包含的数学知识较为广泛.构造法当中数列的构造往往应用于一些特殊的题目当中，主要是针对题目进行分析,构造等差和等比数列，从而优化解题思路.

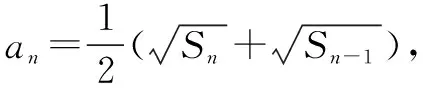
分析基于传统的求解我们需要通过分析数列前几项的和求出一些条件，从而利用数列的通项公式求出Sn的具体表达式.但是这种传统的解题方式往往比较繁琐，所以我们可以利用数列构造法简化解题流程和思路，实现高效化解题.

解析由题目已知，n≥2时，an=Sn-Sn-1.

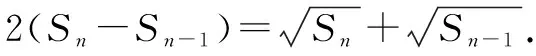
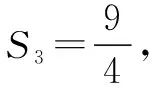
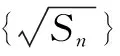
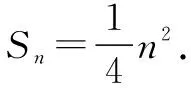
1.4 抽象变直观：向量的构造

在高中，向量不应该局限于单一的知识讨论，而是应该参与高中阶段的数学知识的整合深化，通过利用向量，将抽象问题直观化，将函数问题图形化，从而有效地解决难题，避免了传统的复杂解题过程.

这道题是一类经典的函数问题，能够使用传统的解题方法进行解决，而传统的方法会产生大量的计算步骤，并且容易产生计算错误.如果能够利用向量，使用构造向量法，将有效降低其解题难度.

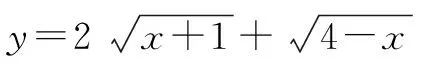
2 构造法在高中解题中的关键点

构造法是基于培育学生的数学思维、创新性和思维敏捷性开展的一种解题方法，学生可以通过具体问题的特征发散思维，发挥数学知识的创新性，从而开展基于函数、图形、方程等手段的构造，将问题直观化、具体化，实现问题的解决.

2.1 构造法运用的前提：审题和题意的理解

在高中数学解题中运用构造法，教师首先要教会学生审题，这是学生开展正确解题的前提.如果学生在处理题目时不重视审题，那么在解题时就会走进误区，会导致过程或结果出现严重偏差或错误.审题时，通过对题目条件的分析和提取，对求证问题展开分析，是否存在隐藏条件，从而揣摩题目的真实解题路径.题意的错误理解直接就造成了解题的出错，所以一定要重视审题工作和深刻理解题意以免错误.

2.2 构造法运用的思维：问题的多角度思考

在高中数学解题中运用构造法，是指学生根据已学知识点而展开的多维度的问题思考，并由此进行了多方位的问题处理.高中数学问题非常灵活，在审清问题以后要求学生灵活运用自己所学知识从不同的视角去思考数学问题，从而让学生能够自己寻找解题的思路，做到构造法的熟练运用.教师应该教导学生跳出框架式解题思维，注重核心素养下的数学思维的培育，督促学生养成知识的活学活用、活学活练，实现教学效率和学习效率的双重提高.

数学问题一般较为灵活，解题思路比较多样，如果从不同的视角去审题，所得出的解题思维方式就会有所不同.教师在学生平时的习题训练当中，一定要督促学生基于自身的实际知识储备和解题经验出发，多角度地开展题目的深度解析，从而开展适合题意的解题方式.在初中刚升入高中的学生中，往往会存在将初中的解题思维带到高中的数学问题中，这也对他们的数学学习带来了一定的困扰.因为这种解题思维的框架已经局限了学生自身，无法跳出解题框架处理问题，导致高中的学习成绩得不到有效提高，另外一方面可能也是因为高中的数学知识架构更加复杂，难度更大.所以，高中生需要的不仅仅是解题方法的学习与应用，更是解题思维和学习思维的革新.教师应该基于这种问题开展针对性的教学，在教学中对学生的解题思维和学习方法做出引导，规范学习习惯，促进学生的数学成绩的有效提高.

2.3 构造法的实践保障：题目的检查整理

题目的检查是必要的.这不仅可以提高学生的解题正确率，更是一个好的学习习惯的养成.高中毕竟要面对高考的考验，而高考的成功不仅仅在于对知识的掌握，还在于知识的运用程度，心态的良好以及学习习惯的养成.教师有针对性地培养学生解题之后的检查和错题整理，不仅可以培养学生的学习习惯，而且可以引导学生自我反思，在解题思维和解题方法上不断自我深化和改变，促进学生提高知识实践能力.而且错题集的整理，可以让学生掌握题型，在以后的学习中举一反三，在复习的时候会发挥出更大的作用.

总之，构造法的展开方式应该是多种多样的，是基于具体问题和已掌握的数学知识的深化利用，是学科核心素养的有效体现，在内容上构造法可以基于数、式、函数、方程、数列、复数、图形、图表、几何变换、对偶、模型建立、反例等方式方法展开.提高对构造法应用的重视，开展以构造法为主体的习题讲解课，帮助学生掌握构造法的应用，打破学生的解题僵化思维，促进学生对于数学知识的活学活用，让学生可以多角度地展开解题分析.教师应该教导学生跳出框架式解题思维，注重核心素养下的数学思维的培育，督促学生养成知识的活学活用、活学活练，实现教学效率和学习效率的双重提高.