考虑温度分布的搅拌摩擦焊搅拌头的焊接力预测模型
翁飞翔, 王庆霞,1b, 吴重军, 孙立凡
(1.东华大学 a.机械工程学院,b.上海航天工艺与装备工程技术研究中心, 上海 201620; 2.上海航天设备制造总厂有限公司, 上海 200240)
搅拌摩擦焊(friction stir welding, FSW)具有焊接质量高、接头缺陷少、工件变形小和绿色环保等优点,在铝合金、镁合金等低熔点合金连接方面得到广泛应用[1]。随着该技术的快速发展,其应用对象逐渐向黑色金属及其他高熔点材料转移,其中钛合金搅拌摩擦焊就是一个值得探索的研究方向[2]。钛合金材料具有抗腐蚀、耐高温和比强度高等优点,目前在宇航领域,尤其是飞行器制造领域得到越来越广泛的应用[1],而搅拌摩擦焊可以克服钛合金熔焊条件苛刻、过程复杂、接头缺陷多及强度低的缺点。研究[2-3]表明,在钛合金搅拌摩擦焊接过程中焊接区域温度往往超过1 000 ℃,并且搅拌头所受载荷是低熔点合金焊接的数倍,搅拌头极易发生剧烈磨损甚至断裂。同时,因设计不当,搅拌头在搅拌摩擦焊接过程中的复杂力、热载荷作用下更易发生破坏[4]。因此,研究钛合金搅拌摩擦焊接过程中搅拌头所受到的焊接力,对搅拌头结构设计及焊接工艺参数选择等是十分重要的。徐天天等[5]和徐博等[6]设计了可安装在焊接主轴前端的力传感器,成功测得了搅拌摩擦焊接过程中的搅拌头受力,但传感器只能在试验后了解搅拌头的受载状况,无法在试验前起指导作用。吴奇等[7]利用有限元软件进行FSW热力耦合分析并计算了搅拌头的受力,但搅拌摩擦焊接过程中的大变形不利于网格重划分[8],因此,此法在计算焊接力时耗时较多,且无法控制预测误差[9]。王腾等[10]假设正压力在搅拌头上均匀分布,初步建立了搅拌头的受力模型,但计算过程中忽略了剪切摩擦,因此焊接力的预测误差较大。Mehta等[11]和Arora等[12]在计算过程中同时考虑库仑摩擦与剪切摩擦,但由于对接头处的温度分布做了等值化处理,致使焊接力的预测精度不高。邓云飞等[13]在研究钛合金的屈服强度时发现,材料的流变应力与材料温度息息相关。因此,在计算过程中考虑温度分布有助于更真实地描述搅拌头的受力状态,提高计算精度。
考虑接头温度分布,根据搅拌头所受的面力建立搅拌头各部位的受力模型,并以钛合金焊接为例,在获得接头温度场的基础上,结合材料强度的温变效应构造正压力函数,据此预测搅拌头所受焊接力,并与试验结果进行对比。
1 考虑温度分布的搅拌头面力分析
在搅拌摩擦焊接过程中,搅拌头与接头材料之间发生挤压与剪切,因此搅拌头承受接头材料给予的面力包括正压力和摩擦力。对于搅拌头而言,搅拌头前进方向的一侧为搅拌材料入口(见图1),由于该入口处接头材料的速度方向与搅拌头前进方向相反,故为压力入口。搅拌头上与前进方向相反的一侧为材料出口,由于接头材料在该侧并未挤压搅拌头,仅随搅拌头流动,故可近似认为无正压力,设为压力出口。焊接过程中搅拌头上的面力分布如图2所示。
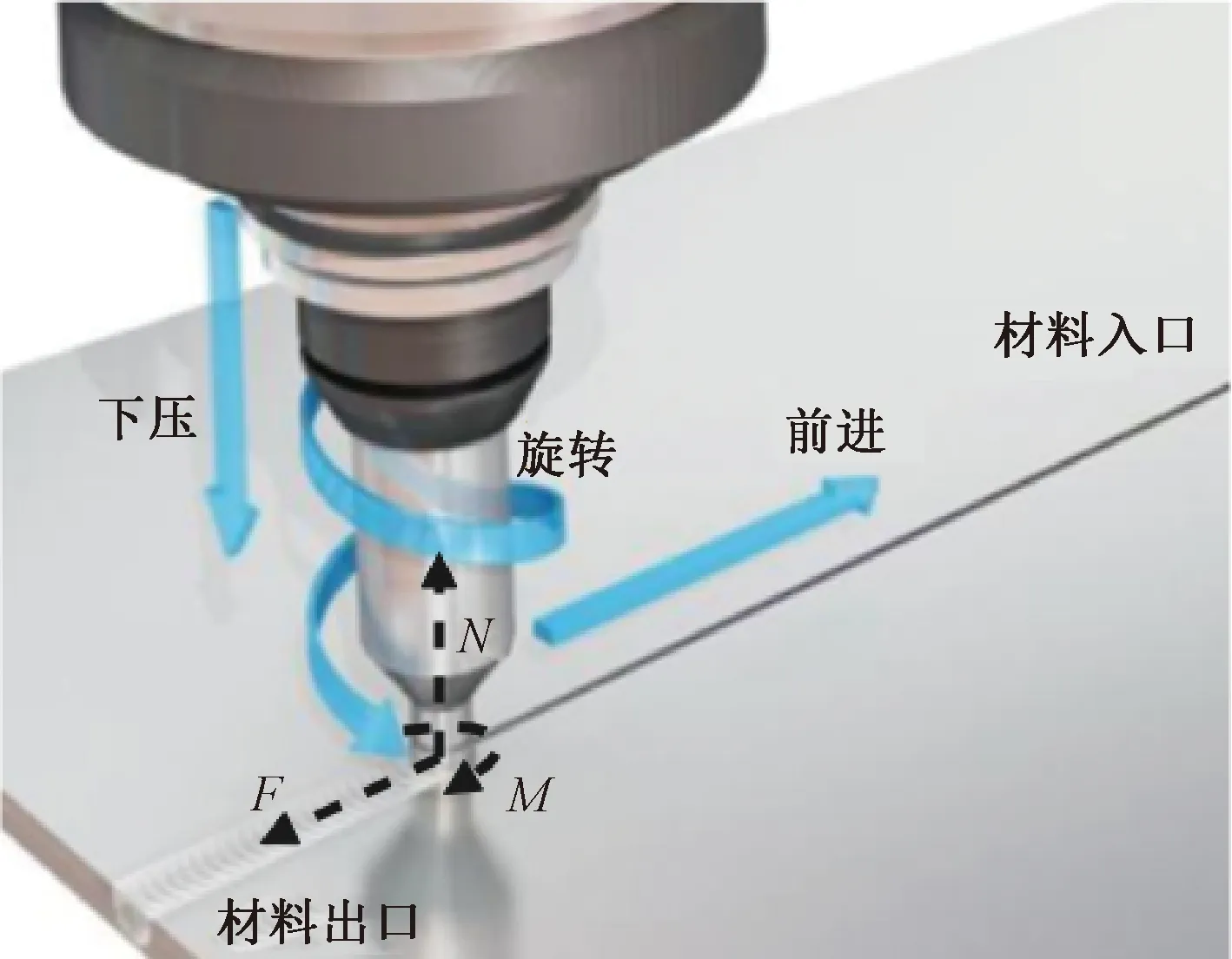
图1 搅拌摩擦焊接示意图Fig.1 Diagram of friction stir welding
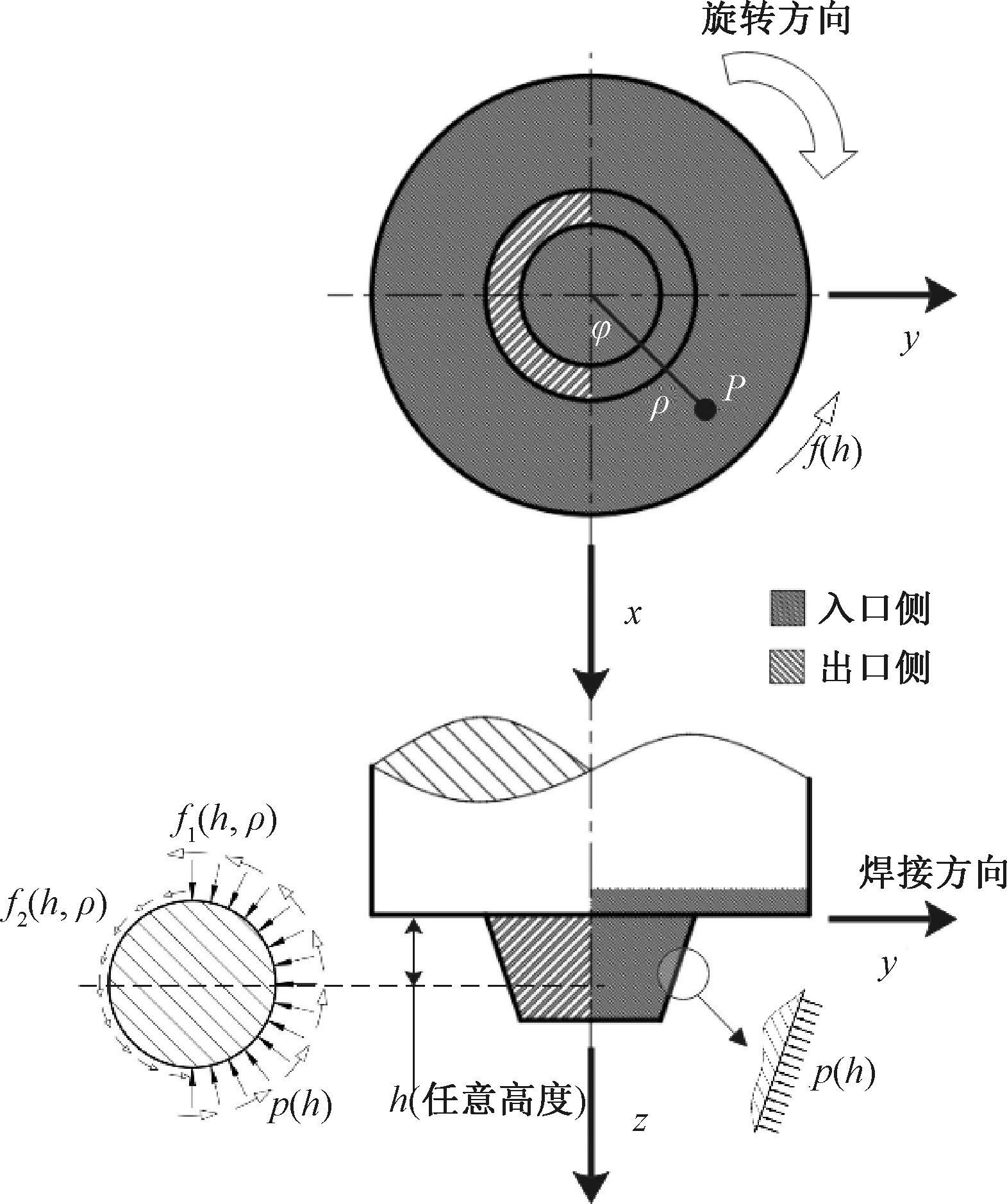
图2 摩擦焊接过程搅拌头面力分布及方向Fig.2 Distribution and direction of surface force on stirring head during welding
焊接过程中接头材料因发生塑性变形而流动,故将搅拌头所受正压力设为工件材料的屈服强度[11]。同时,接头材料在焊接过程中各位置受热与散热状态不同[14],导致接头温度场呈非均匀分布,接头材料的最高温度可达其熔点的80%,而对导热率较低的合金如钛合金而言,接头上、下的温差可达200 ℃,甚至更高[3]。因此,温度对材料屈服强度的影响不可忽略。据此,图2中任意高度h处,搅拌头受到的正压力p可表示为
p(h)=σw(t(h))
(1)
式中:σw为工件材料的屈服强度;t(h)为工件材料在高度h处的温度。
研究[15-17]表明:任意高度h处的焊接区域温度以搅拌头中心为基准呈非对称分布,但前进侧与后退侧温差较小,此处取搅拌针外圆周面上的最小温度为t。
搅拌头与工件之间的接触状态不同,因此搅拌头所受摩擦力也不同。为了统一,将摩擦力表示为
f(h)=δμp(h)+(1-δ)τw(h)
(2)

根据文献[19],相对滑移系数δ与库仑摩擦因数μ分别为
(3)
μ(ρ)=0.5×exp(-δ(ρ)ωρ)
(4)
式中:ω为搅拌头角速度;ρ为搅拌头上任意点P距轴线的距离,如图2所示。
因此,搅拌头入口侧和出口侧单位面积所受摩擦力f1(h,ρ)和f2(h,ρ)分别为
f1(h,ρ)=δ(ρ)μ(ρ)p(h)+
(1-δ(ρ))τw(h)
(5)
f2(h,ρ)=(1-δ(ρ))τw(h)
(6)
综上可知,正压力与接头各点的温度有关,而摩擦力除了与温度相关外,还与各点的滑动状态及摩擦因数有关。
2 搅拌摩擦焊过程中焊接力建模
在搅拌摩擦焊接过程中,接头材料发生变形需克服变形抗力和摩擦阻力,其总和构成作用在搅拌头上的焊接力。为便于研究,通常将焊接力分解为沿主轴方向的顶锻力、沿焊接方向的前进抗力,以及绕主轴轴线的焊接扭矩,分别用N、F和M表示,如图3所示。其中:Ns、Nnc和Nnp分别为搅拌轴肩、搅拌针侧面及搅拌针底面受到的顶锻力;Fsc和Fnc分别为搅拌轴肩和搅拌针侧面受到的前进阻力;Ms和Msc分别为搅拌轴肩及其侧面所受的摩擦扭矩;Mnc1和Mnc2分别为搅拌针焊接前进侧(搅拌针侧面的入口侧)及后退侧(搅拌针侧面的出口侧)所受摩擦扭矩;Mnp为搅拌针底面所受摩擦扭矩。本文建立的受力模型均采用移动柱坐标系ρφz进行计算。

图3 焊接过程中搅拌头各部位受力图Fig.3 Force diagram of each part of the stirring head during welding
由图2可知,对搅拌头的轴肩及搅拌针所受到的微元面力进行积分,即可分析焊接过程中搅拌头受到的宏观力及力矩。由此推导出搅拌轴肩、搅拌针侧面及底面受到的顶锻力Ns、Nnc和Nnp分别为
(7)
式中:Rs、Rd、Rp分别为轴肩、搅拌针根部及底面的半径;H和α分别为搅拌针的长度和锥角。
搅拌轴肩和搅拌针的侧面受到的前进阻力Fnc和Fsc分别为
(8)
式中:Fnf为前进阻力Fnc的线载荷,即搅拌针侧面单位高度上的前进阻力;φ为搅拌头各横截面上的周向角,如图2所示;ap为轴肩下压量。
在搅拌摩擦焊接过程中,与搅拌头的旋转线速度相比,前进速度较小,因此可忽略不计。由此可认为搅拌头各部位所受摩擦力在前进方向上的分力相对于yz平面(见图2)呈反对称分布,即其合力为0。因此,搅拌头受到的前进阻力如式(8)所示。
设h为搅拌头上任意高度位置,那么搅拌头在任意高度处的弯矩为
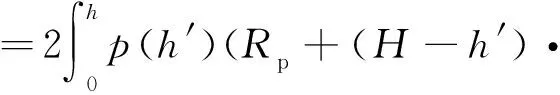
tanα)cosα(h′-h)dh′
(9)
因此,搅拌针侧面所受的前进阻力Fnc的作用高度hF可表示为
hF=B(0)/Fnc
(10)
在搅拌摩擦焊接过程中,搅拌头各部位所受摩擦力微元沿周向进行积分,可得搅拌头所受到的摩擦扭矩。其中,搅拌轴肩及其侧面受到的摩擦扭矩Ms和Msc分别为
(11)
式中:ρ为面积微元距主轴轴线的距离,如图2所示。
搅拌针侧面的入口侧与出口侧所受的摩擦扭矩Mnc1和Mnc2分别为
(12)
搅拌针的底面受到的摩擦扭矩Mnp为
(13)
综上所述,搅拌头在摩擦焊接过程中所受的顶锻力、前进阻力和扭矩分别为
(14)
值得注意的是,在搅拌摩擦焊的下压阶段,由于搅拌头并未发生横移,因此,此时材料的入口侧与出口侧所受面力一致,故其所受的顶锻力、前进阻力和力矩可表示为
(15)
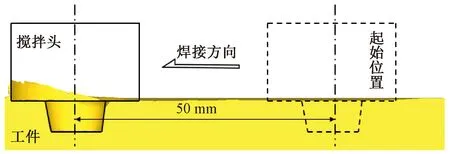
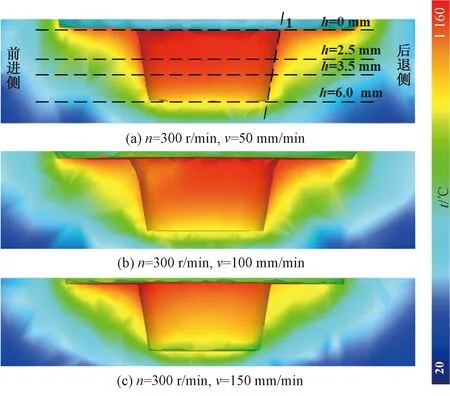
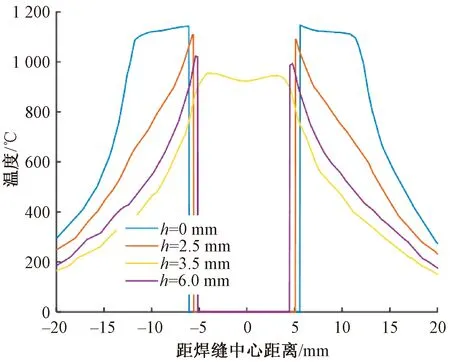
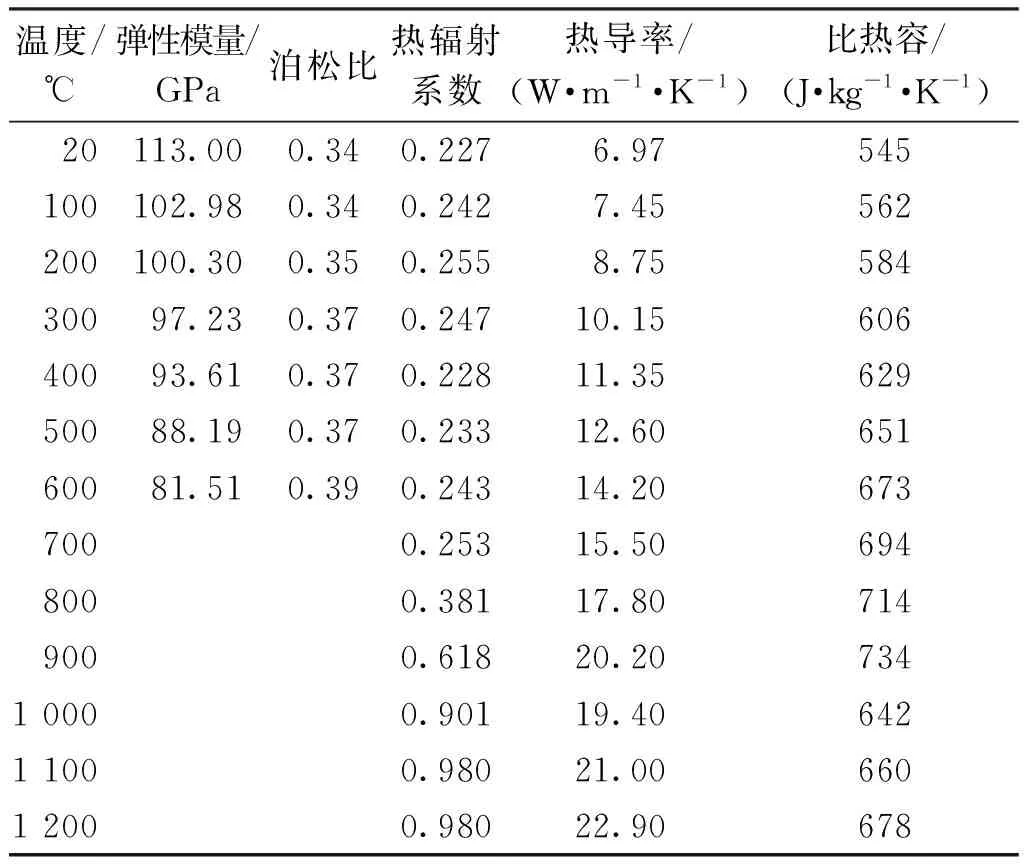
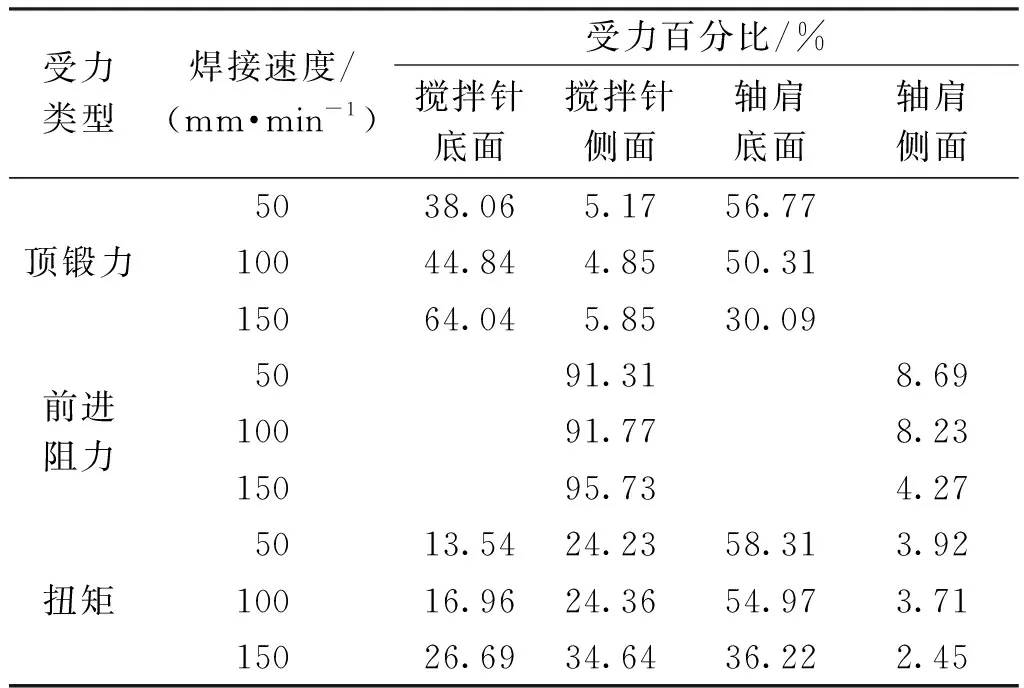
式中:hi为搅拌针的压入深度;hs为搅拌轴肩的压入深度,hs=hi-H;λ为轴肩受力系数。当hi 对比式(14)和(15)可知,搅拌头在使用过程中所受的最大顶锻力发生在下压阶段的最后时刻,这与文献[20-21]的试验结果一致。这是由于式(15)中的顶锻力N较式(14)多一个Nnc,此外下压阶段轴肩与工件的接触时间较短,产生热量较少,因此各点温度均低于焊接阶段,导致搅拌头所受面力较大。 采用Deform-3D软件进行搅拌摩擦焊接温度场模拟,详细过程参照文献[14]。为防止焊接过程中的网格畸变,采用自适应网格划分及时纠正错误网格,焊接示意图如图4所示,焊接距离为50 mm。搅拌头材料为硬质合金,性能参数如表1所示,几何尺寸分别为Rs=12.5 mm,Rd=6 mm,Rp=5 mm,H=6 mm。接头材料为钛合金,物理参数与热物性参数如表2所示。焊接时,主轴转速n取300 r/min,焊接速度v依次取50、100与150 mm/min。各工艺参数下的接头温度场如图5所示,图中虚线1所示部位为接头与搅拌头后退侧的接触区。提取图5中不同高度处的焊接区温度,结果如图6所示。 图4 焊接过程示意图Fig.4 Diagram of welding process 图5 工件与搅拌头的接触区温度场Fig.5 Temperature field of the contact area between workpiece and stirring head 图6 温度曲线变化图(n=300 r/min,v=50 mm/min)Fig.6 Diagram of temperature curve changes (n=300 r/min,v=50 mm/min) 表1 硬质合金的物理及热力学性能[22]Table 1 Physical and thermodynamic properties of cemented carbide[22] 表2 钛合金的物理及热物性参数[22-23] 由图6可知,同一高度上,工件与搅拌头接触处温度最高,且前进侧温度略高于后退侧,为5~30 ℃。在h=0,即靠近轴肩处,温度呈先升高后快速下降的趋势,这是由于工件与轴肩接触区的摩擦产热减缓了温度的下降速率,同时轴肩接触区的温差在40 ℃以内。此外,接触区的最小温度出现在搅拌针底面中心位置附近,这可能是由搅拌针底面圆心处线速度最小,摩擦产热量最低所导致的。由此可见,可将后退侧虚线1上相应高度的温度作为搅拌头受力预测模型中的参考温度。 图7为不同焊接速度下虚线1上的温度。其中,方框所代表的几个离散点为文献[20]中焊接试验所测得的温度值。对比可知,本文仿真结果与文献[20]试验结果的相对误差为0.75%~3.40%,说明仿真结果可靠。此外,图7显示,随高度h的增加,接头温度逐渐降低,同时焊接速度对下搅拌区温度的影响远大于上搅拌区,随着焊接速度的增大,上搅拌区温度变化较小,而下搅拌区温度明显减小。其中的上、中、下搅拌区分别为将接头高度三等分后的上部、中部和下部。 图7 接头与搅拌头后退侧接触区温度Fig.7 Temperature of contact zone between welding joint and backward side of stirring head 文献[13]对钛合金的高温力学性能进行研究。为估算不同温度下搅拌头所受的正压力,采用最小二乘拟合得到钛合金屈服强度与温度之间的关系,如图8所示,拟合所得函数如下: σw(t)=a·[t4t3t2t1t0]T (500 ℃≤t≤1 300 ℃) a=[3.76×10-9-1.69×10-52.55×10-2 -18.27 5.05×103] (16) 式中:a为系数向量。 图8 钛合金屈服强度随温度的变化曲线Fig.8 Yield strength curve of titanium alloy with temperature 根据图7所示温度分布曲线,拟合得到各工艺参数下接头与搅拌头后退侧接触区不同高度h处的温度函数,如式(17)所示。 (17) 式中:t1(h)、t2(h)、t3(h)及A1、A2、A3分别为焊接速度50、100、150 mm/min下的温度函数与温度系数向量;h为高度向量。 将式(17)代入式(16),即可建立正压力与高度h的关系p(h),如图9所示。由图9可知,随着高度h的增加,搅拌头所受正压力逐渐增大,并且沿搅拌针长度方向存在一个临界高度值hc,在该位置点之前搅拌头所受正压力呈缓慢线性增加,在该点之后,正压力快速增长。焊接速度越大,hc越小,向着轴肩方向偏移。由此可见,由焊接速度变化引发的焊接温度的显著变化对搅拌头所受正压力影响很大,即焊接温度在搅拌头受力计算中不容忽略。 图9 正压力随h的变化关系Fig.9 Relationship between positive pressure and h 将所计算的正压力p(h)代入焊接力预测模型,计算焊接阶段搅拌头所受的顶锻力、前进阻力与扭矩,如图10中虚线所示;图10中的实线表示文献[20]中的物理试验测试结果;点划线表示忽略不同高度方向上的温度差异[11],将接头温度统一设为工件熔点tm的80%,即令p=0.8tmσw所得的焊接力。 图10 焊接力与焊接速度的变化关系对比Fig.10 Comparison of the change relationship between welding force and welding speed 由图10可知:采用本文计算模型预测的焊接力与文献[20]的试验结果的最大相对偏差在20%以内,同时预测结果在传感器所测焊接力的波动范围之内;而忽略温度分布的计算结果一方面将焊接温度场进行了等值化,另一方面未考虑工艺参数变化引起的温度场变化,因此与试验结果的最大相对误差为80%。由此可见,本文建立的计算模型具有可靠性。此外,随着焊接速度的增加,接头上各点将经历更快的热循环,即在搅拌头靠近时更快地升温,受热时间相应降低。上搅拌区由于靠近轴肩,受轴肩接触区面积大、产热量高的影响,因此在焊接速度加快后,温度下降并不明显;而中下搅拌区离轴肩较远,并且本身的产热量远低于轴肩,因此在焊接速度加快、受热时间缩短后,温度明显下降;中下搅拌区温度的明显降低又提高了该区域接头材料的强度,使得搅拌头在运动过程中承受更大的正压力与摩擦力,从而使焊接力逐渐增大。 表3为据本文预测模型计算出的搅拌头上各部位焊接力的分布百分比。由表3可知,随着焊接速度的增加:搅拌针底面承受的顶锻力和扭矩,以及侧面承受的前进阻力和扭矩逐渐增大;而轴肩底面承受的顶锻力和扭矩,以及轴肩侧面承受的前进阻力和扭矩相应减小。这是由于随焊接速度的增加,工件与搅拌针底面及侧面接触区的温度下降,界面压力升高;而在轴肩接触区,焊接温度对接头温度的影响较小,即界面压力无较大波动。因此,搅拌针承受的各项力的百分比增大,而由轴肩承受的各项力的百分比下降。 表3 搅拌头各部位的受力百分比 搅拌头各部位面积百分比依次为搅拌针底面11.45%、搅拌针侧面30.64%、轴肩底面55.05%、轴肩侧面2.86%。由此可见,在焊接速度较低时,轴肩底面承受的顶锻力百分比与其面积百分比相近,但其他各部位所受顶锻力与其面积百分比相差较大,因此文献[12,24]在对搅拌头进行应力分析时,将所测得的顶锻力简单地按各部位面积百分比进行计算是不合理的。前进阻力由搅拌针侧面和轴肩侧面共同承受,但主要是由搅拌针侧面承受。在低焊接速度下,扭矩在搅拌头各部位上的百分比接近各部位面积百分比。这是由于扭矩近似为面积与摩擦力的乘积。在低焊接速度下,上、下搅拌区温度相近,因此上、下搅拌区搅拌头所受摩擦力差值较小;但在高焊接速度下,上、下搅拌区温差增大导致摩擦力差值增大,因此各部位扭矩百分比与其面积百分比的误差也相应增大。 图11为不同高度上前进阻力Fnc的线载荷分布,图中线载荷Fnf(h)和作用高度hF分别由式(8)和(10)得出。 图11 搅拌针上前进阻力Fnc的线载荷分布Fig.11 Linear load distribution of forward resistance Fnc on pin (1)随着竖直方向高度的增加,搅拌头所受正压力增大;随着焊接速度的增大,上、下搅拌区正压力差值增大,但上搅拌区正压力的增长幅度较小,而下搅拌区正压力增长明显。 (2)忽略温度分布的计算模型的预测误差远大于考虑温度分布的焊接力预测模型,而在本文给出的实例中,考虑温度分布的预测模型的预测数值均在传感器所测数值的波动范围内。 (3)随焊接速度的增大,搅拌头所受焊接力增大,其中搅拌针承受的各项力百分比增加,而轴肩承受的各项力百分比下降;搅拌头各部位所受扭矩百分比与各部位面积百分比相近,尤其是在低焊接速度下,而顶锻力百分比与其面积百分比相差较大。 (4)前进阻力主要由搅拌针承受,随着搅拌针长度的增加与焊接速度的增大,前进阻力显著增大,焊接速度的增大还将导致前进阻力的作用点下移,在搅拌针根部产生更大的弯矩。因此为保证搅拌头的正常使用,应采用更低的焊接速度和更短的搅拌针。3 焊接力预测模型实例及分析验证
3.1 接头温度分布模拟


3.2 搅拌头所受正压力估算


3.3 搅拌头所受焊接力分析

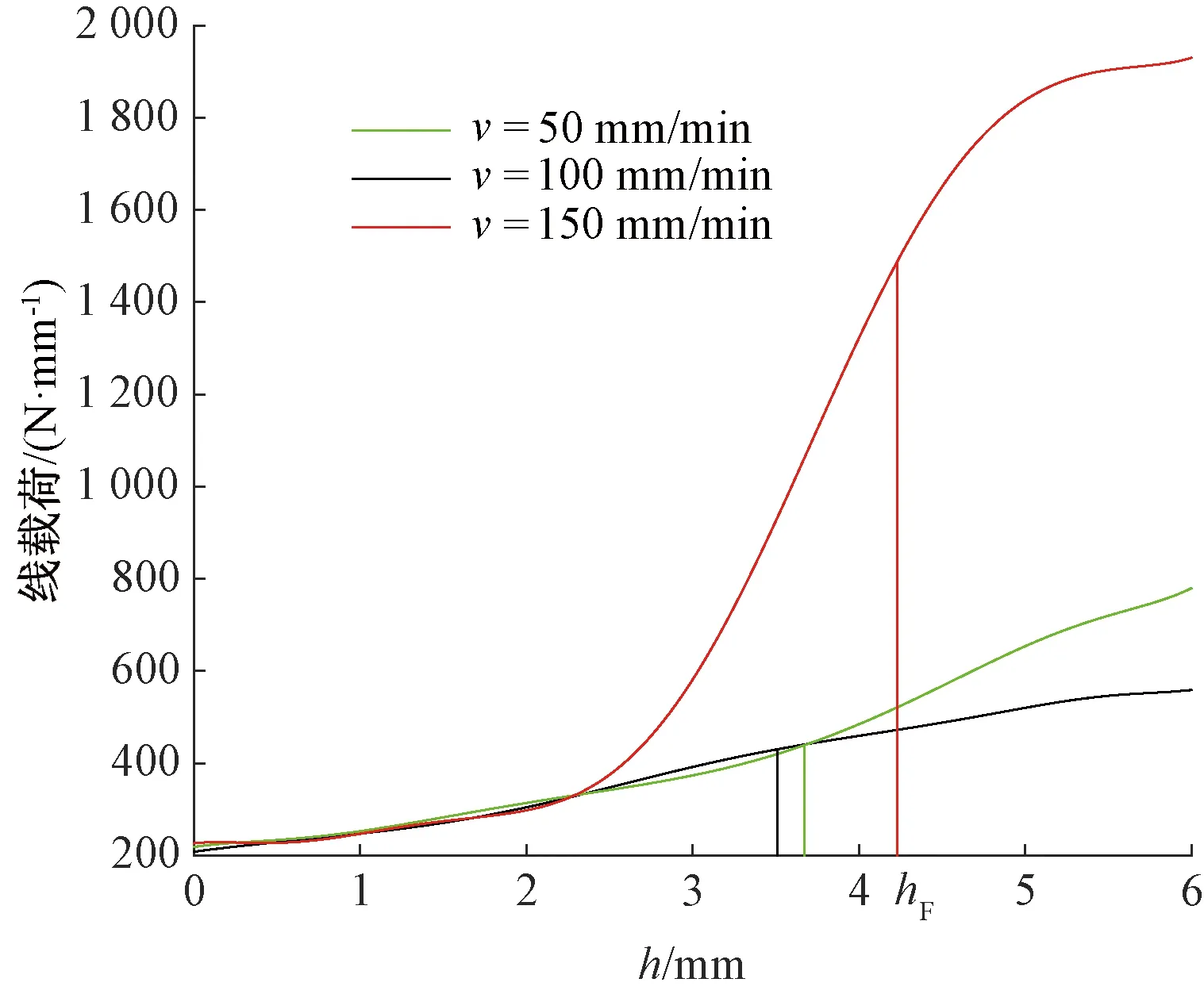
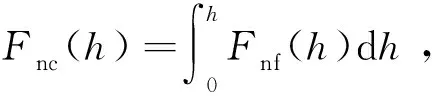
4 结 论

