表贴式永磁交流伺服电机永磁体涡流损耗降耗方法

王威海， 华 华,2， 孔建会， 舒 畅， 陈家新

(1.东华大学 机械工程学院， 上海 201620；2.宣城市气象局，安徽 宣城 242000)

永磁交流伺服电机因具有体积小、能量密度高、效率高等特点，被广泛应用于航空航天、船舶、新能源汽车等领域[1-3]。但永磁交流伺服电机中含有大量的电流-时间谐波与空间谐波，这些谐波会在电机转子中感应出涡流，从而引起涡流损耗。转子位于电机内部，散热比较困难，导致温度逐渐升高，特别是电机中的永磁体部分在温度过高时会发生不可逆的热退磁，严重影响电机的运行可靠性和寿命[4-5]。因此，研究永磁体中的涡流损耗问题对于设计高效节能的永磁交流伺服电机具有非常重要的意义。安忠良等[6]和刘福贵等[7]研究了气隙长度、槽口宽度、永磁体分段等电机结构参数对永磁体涡流损耗的影响；Dajaku等[8-9]和Bilyi等[10]研究发现，在定子铁心中添加磁障结构，可以削弱磁动势谐波的幅值，从而降低永磁体内的涡流损耗；Gundogdu等[11]和Choi等[12]研究发现，对于嵌入式转子结构的永磁同步电机，在转子d轴方向添加磁障结构可有效降低涡流损耗；宋骄等[13]对谐波磁场产生的源头——绕组进行研究，结果表明，设计的绕组结构能够有效削弱绕组磁动势谐波，降低永磁体涡流损耗。

表贴式永磁电机在高速旋转时，往往需要使用护套对永磁体进行固定。佟文明等[14]研究发现，金属护套会明显增加转子的涡流损耗，并且护套厚度受限于气隙长度。因此研究永磁体的涡流损耗时，还需要考虑永磁体的安装问题。本文以表贴式结构的永磁电机为研究对象,提出一种转子q轴开T型槽的方法，利用有限元软件Maxwell建立1台功率为200 W的交流伺服电机的模型，用于分析永磁体极弧系数与电机转矩和永磁体涡流损耗之间的变化规律，并在此基础上详细研究转子q轴开T型槽对永磁体涡流损耗的影响。

1 永磁体涡流损耗的计算模型

在永磁同步电机中，将与电机转子保持同步旋转的磁场称为基波旋转磁场，反之称为谐波磁场。谐波磁场会在电机永磁体内感应出涡流，从而引起涡流损耗。目前广泛使用二维有限元法分析并计算电机的电磁性能。在忽略电机的端部效应、位移电流和假设铁磁材料各向同性的前提下，将复杂的三维模型转换为二维模型。在有限元仿真软件Maxwell提供的二维瞬态场求解器中，电机的磁场方程[15]可以描述为

(1)

式中：ν为运动部件的速度；A为矢量磁位；t为时间；Js为源电流密度；σ为电导率；Hc为永磁体的矫顽力。

在此基础上，将求解区域剖分成有限多个单元，单元内部通过插值方法求取矢量磁位A的值，则永磁体内每一点的涡流密度Je可表示为

(2)

电机永磁体内涡流损耗Pm的计算公式可表达为

(3)

式中：L为永磁体轴向的长度；S为永磁体的横截面积。

利用Maxwell计算永磁体内涡流的分布，从而计算涡流损耗。本文设计了1台极对数p=5、槽数z=12、额定功率PN=200 W的样机，用于研究开槽对永磁体涡流损耗的影响。电机中定子的内、外直径分别为37.0和58.0 mm，转子的内、外直径分别为16.0和36.6 mm，磁极厚度为2.5 mm，铁心厚度为20.0 mm。电机模型如图1所示。

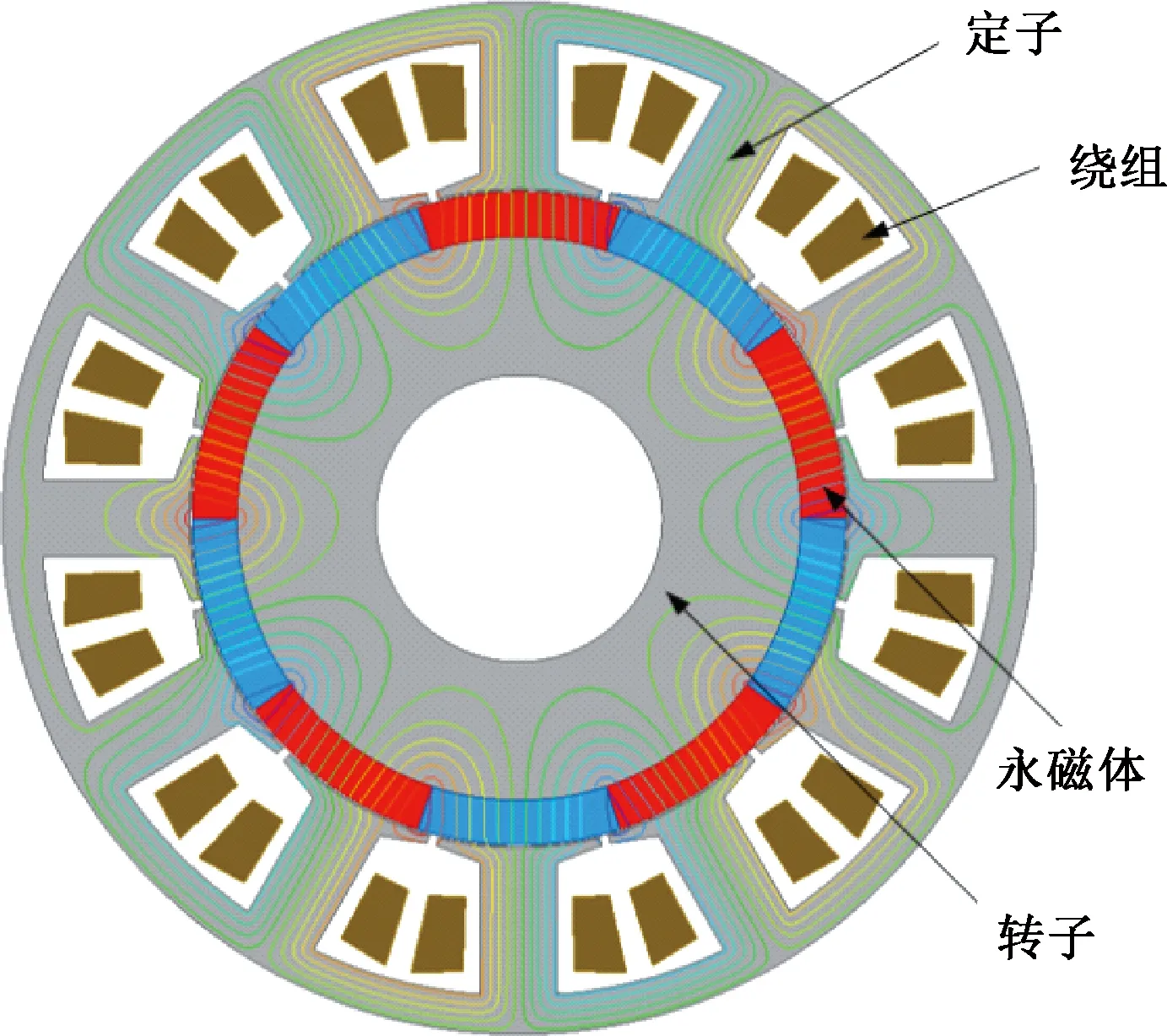
图1 电机有限元模型Fig.1 The finite element model of the motor

2 永磁体的极弧系数分析

在转子q轴区域开槽时，电机永磁体的极弧系数会发生变化，从而影响电机额定转矩和永磁体涡流损耗。因此，在确定开槽宽度前，需对由永磁体极弧系数的变化带来的影响进行分析。设单个磁极对应的机械角度为β，如图2所示。永磁体极弧系数的大小用单个永磁体对应的电角度θ来表示，则θ=pβ，其中p为极对数。随着θ的变化，电机额定转矩和永磁体涡流损耗的变化如图3所示，其单位电角度对应的增量变化如图4所示。

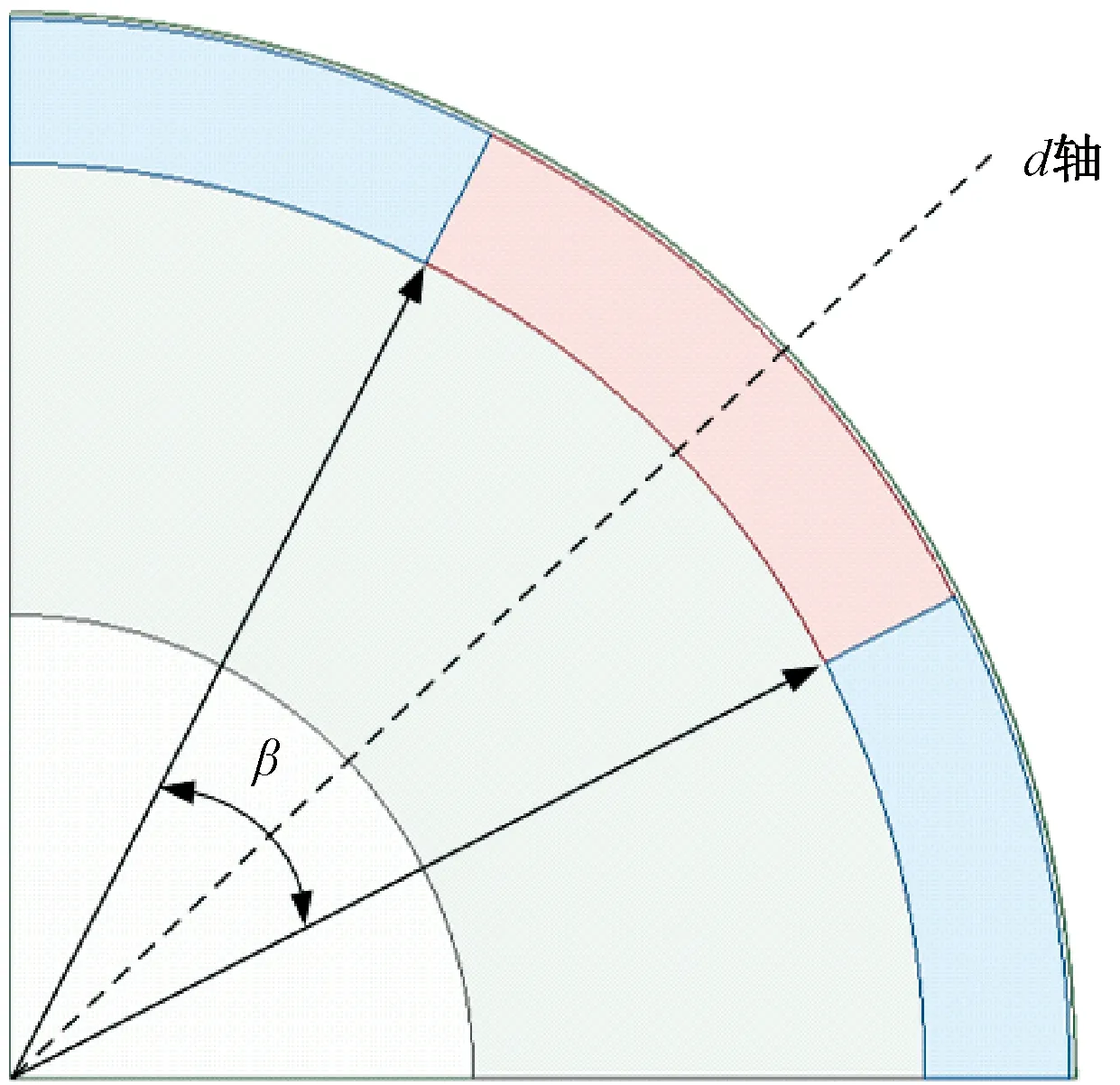
图2 磁极示意图Fig.2 Magnetic pole schematic

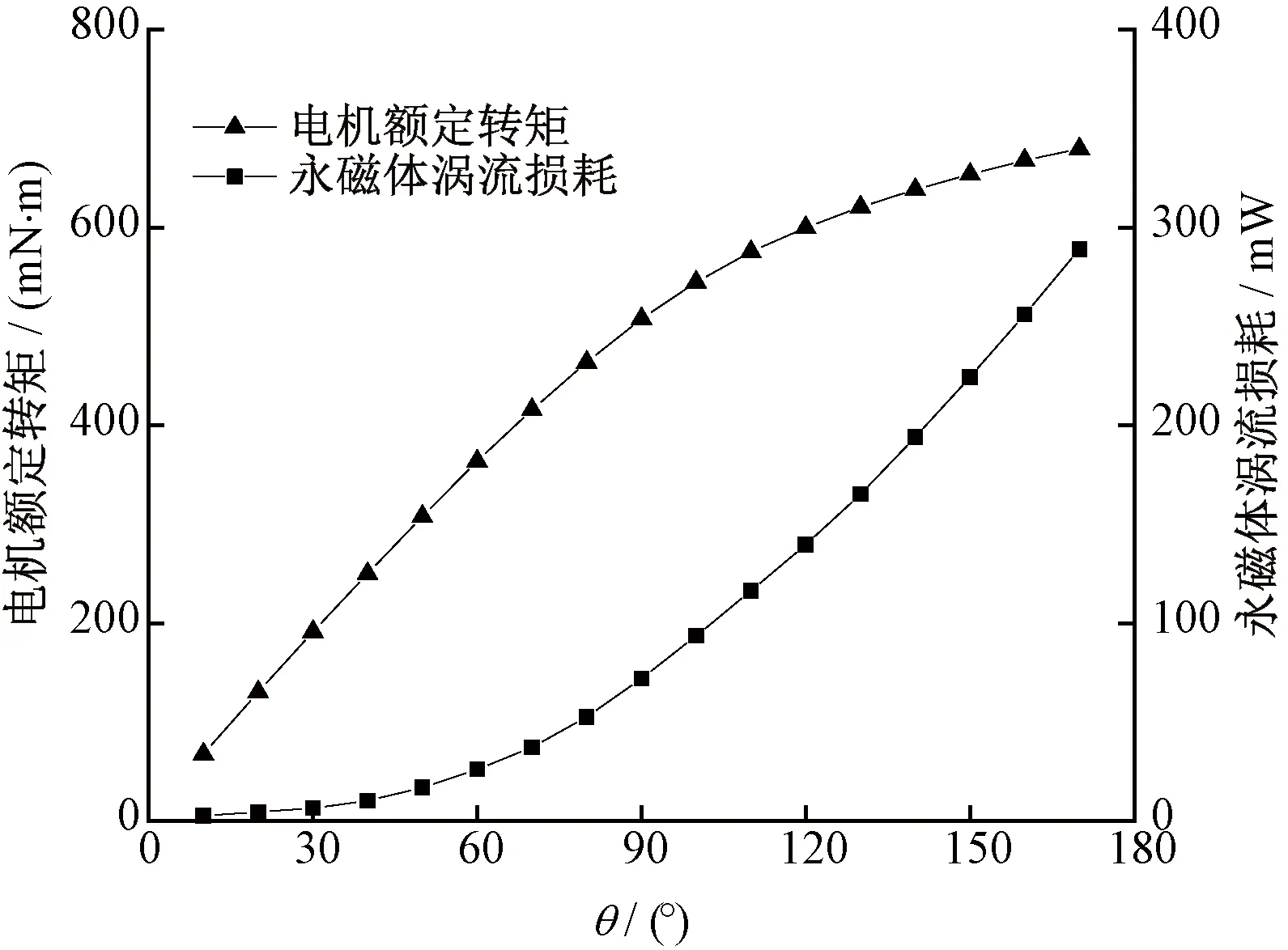
图3 永磁体电角度对电机额定转矩和永磁体涡流损耗的影响Fig.3 Influence of permanent magnet electrical angle on motor rated torque and permanent magnet eddy current loss

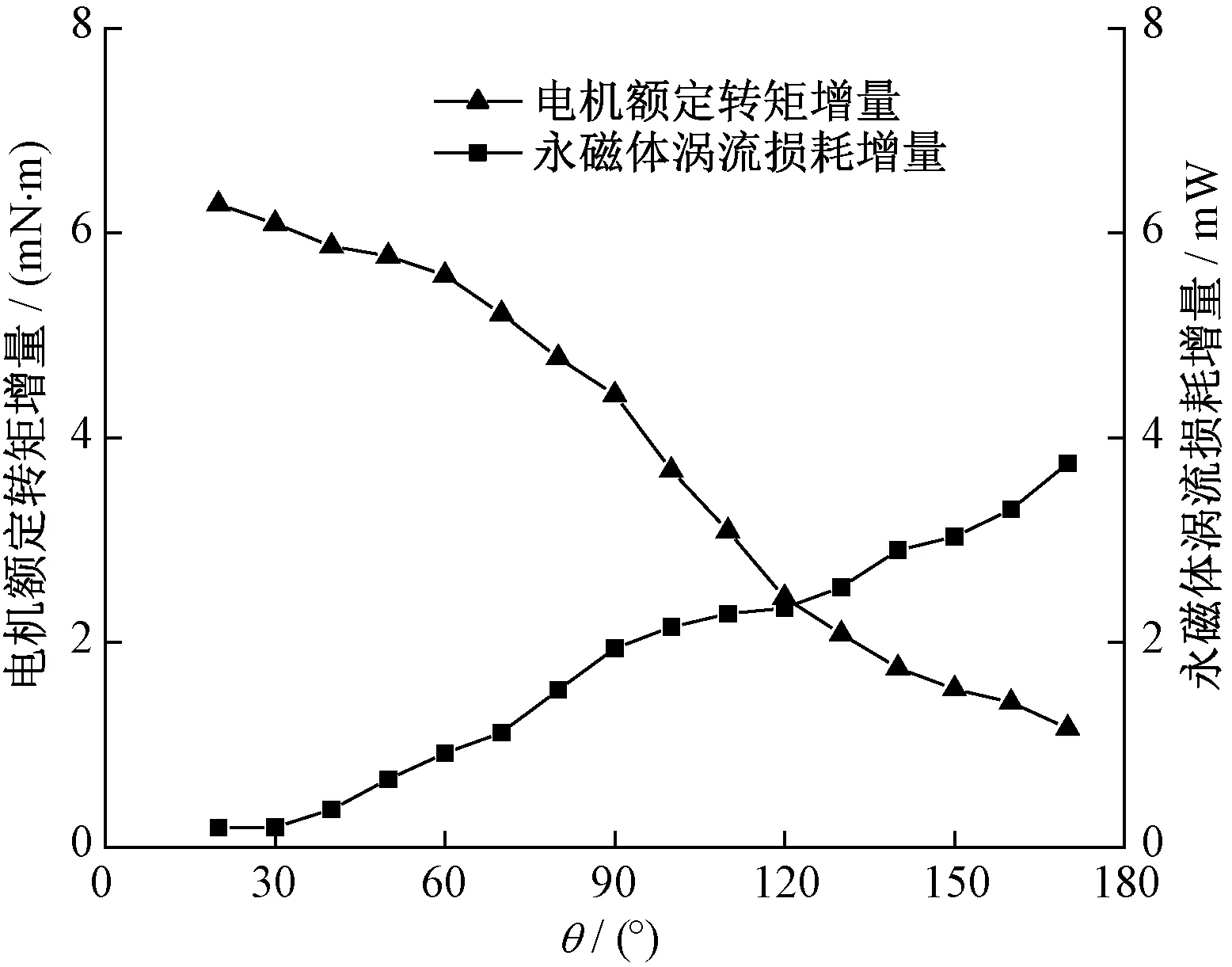
图4 永磁体电角度对电机额定转矩增量和永磁体涡流损耗增量的影响Fig.4 Influence of permanent magnet electrical angle on the increase of motor rated torque and permanent magnet eddy current loss

由图3和图4可以看出，电机额定转矩和永磁体涡流损耗均随着电角度θ的增加而增加，但是转矩的增量随电角度θ的增加呈减小趋势，而永磁体涡流损耗的增量则从较低的水平开始快速增大。

为了进一步研究电机额定转矩和永磁体涡流损耗的变化规律，定义电机额定转矩增量与永磁体涡流损耗增量的比值为K，表达式为

(4)

式中：ΔT和ΔPm分别为单位永磁体电角度对应的电机额定转矩增量和永磁体涡流损耗增量。

K值表征的是永磁体电角度增加对电机额定转矩和永磁体涡流损耗的贡献比，其变化规律如图5所示。从图5可以看出，K值随永磁体电角度θ的增加呈减小趋势。当θ>120°时，K<1，此时单位永磁体电角度的增加对永磁体涡流损耗的贡献大于对电机额定转矩的贡献，并且该趋势在逐渐增强。

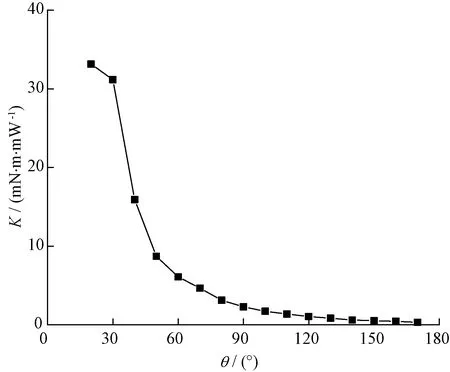
图5 永磁体电角度对K值的影响Fig.5 Influence of magnet electric angle on K value

转子的磁密云图如图6所示。从图6可以看出转子磁密的空间分布情况。由于永磁电机磁密变化具有空间和时间周期性，因此可以看出转子磁密变化在q轴区域附近最明显。进一步计算流经路径L1、L2时磁通量随时间的变化，结果如图7所示。计算得到L1上磁通量的波动率为1.5%，L2上的磁通量波动率为5%，表明L2所在区域更容易产生涡流损耗，验证了前面分析所得的结论。

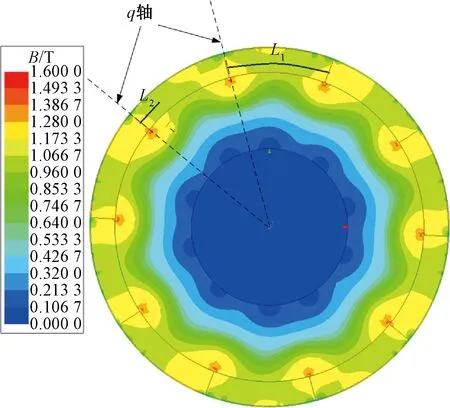
图6 转子的磁密云图Fig.6 Magnetic density cloud map of rotor

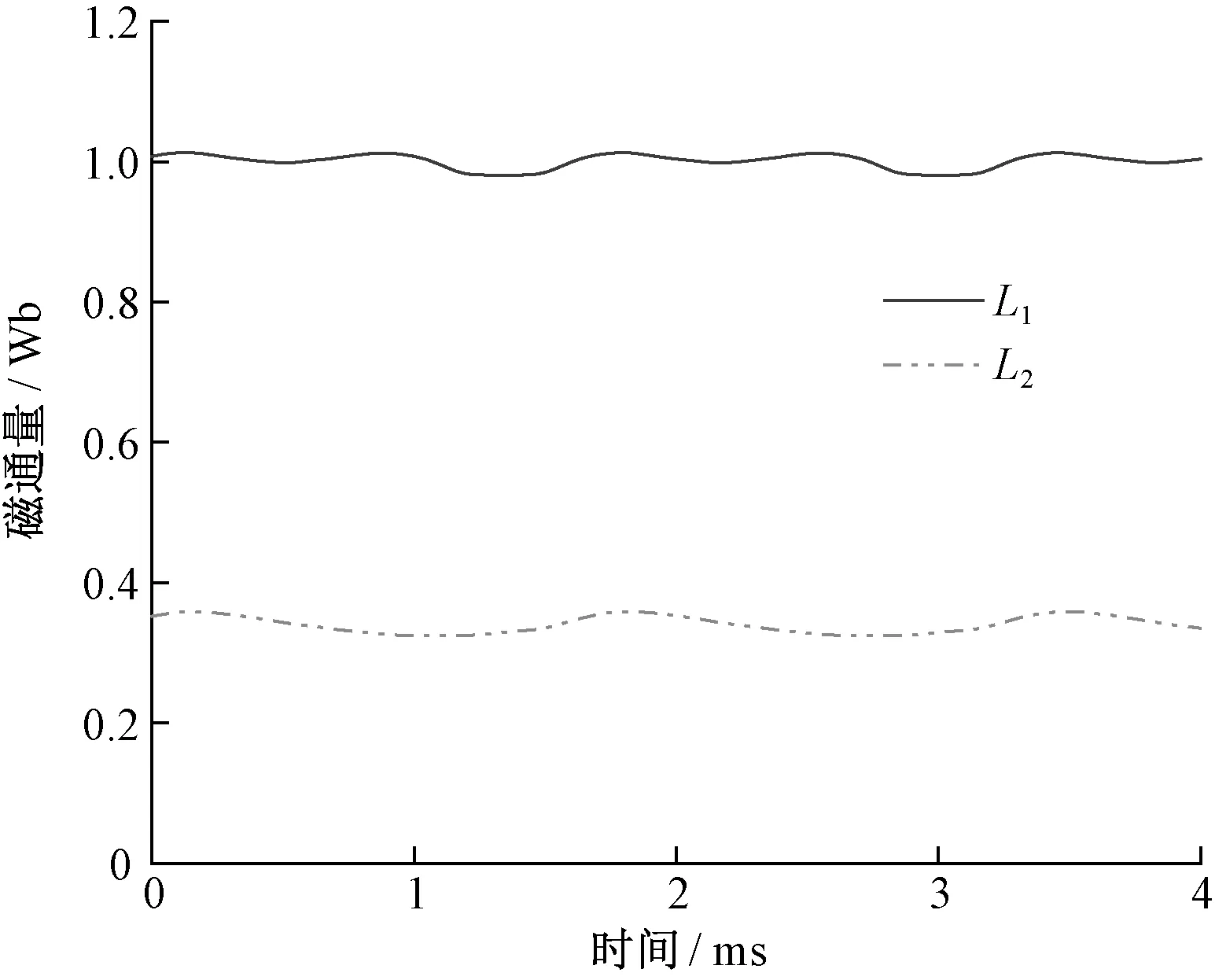
图7 不同路径磁通量变化情况Fig.7 Variation of magnetic flux at different paths

图8 电机转子q轴开T型槽Fig.8 Opening T-slots at q-axis of the rotor

3 T型槽对永磁体涡流损耗的影响

由永磁体极弧系数的分析可知：q轴附近永磁体极弧系数的变化对电机额定转矩影响较小；适当削减极弧系数能够有效降低涡流损耗。结合固定装置的尺寸要求，将开槽宽度设定为0.5 mm。由于转子开直槽时槽深会受到转子轭部的径向长度的限制，因此考虑将直槽改成T型槽，如图8所示。电机转子q轴开T型槽，除了可以降低转子永磁体的涡流损耗，还可以放置固定装置用于固定表贴式磁极的位置，适用于转子高速转动的场合，并且不需引入轴套，降低了装配难度。以下对T型槽的结构进行分析。

在转子轭部开T型槽时，空气磁阻较转子铁心磁阻更大，导致磁路上转子部分的磁阻增大，从而削弱了谐波磁场的强度，对气隙圆周方向的气隙磁通分布进行分析可以证实这一点。开槽后气隙磁通谐波削弱情况如表1所示。由表1可知，开T型槽对基波的影响较小，但对其他高次谐波则有较为明显的削弱作用。

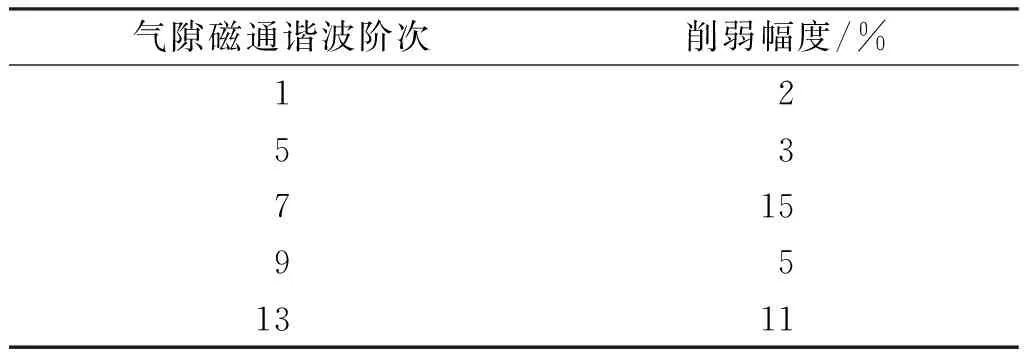
表1 T型槽对气隙磁通谐波的削弱效果

由式(3)可知，永磁体涡流损耗与永磁体轴向涡流密度的平方成正比。对永磁体内轴向涡流密度进行分析，通过傅里叶分解得到各阶次涡流密度的幅值如图9所示。

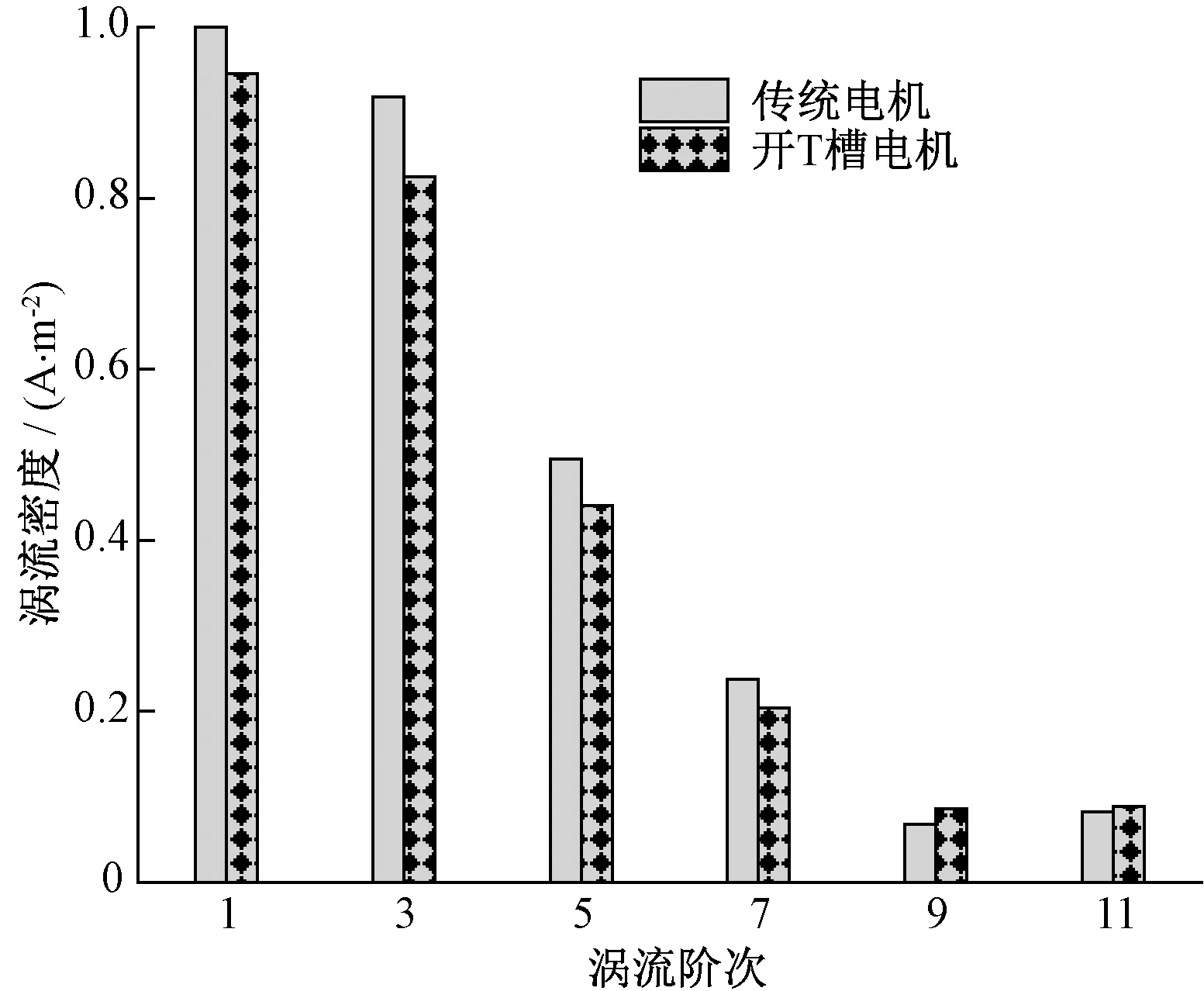
图9 永磁体涡流密度幅值Fig.9 The magnitude of eddy current density in magnet

从图9可以看出：转子开T型槽后，永磁体涡流密度各阶次幅值均呈下降趋势。其中，涡流阶次为1时涡流密度幅值下降了5.4%，涡流阶次为3、5、7时涡流密度幅值则分别下降10%、11%和14%。由此可见，电机转子q轴开T型槽能够有效削弱永磁体内的涡流。

通过有限元软件计算得到转子开T型槽后的永磁体涡流损耗。转子q轴开T型槽后，永磁体涡流损耗从297 mW下降为253 mW，涡流损耗减少了15%。转子q轴开直槽和开T型槽时，永磁体涡流损耗与槽深的关系如图10所示。从图10可以看出，随着槽深的增加，两种电机结构的永磁体涡流损耗均有所下降，当槽深达到一定值时，两种转子结构对永磁体涡流损耗的削弱效果相近。此外，T型槽的槽深为3.5 mm时对永磁体涡流损耗的削弱效果与直槽槽深为5 mm时相同。因此，在转子径向开槽空间受限的情况下，选择q轴开T型槽可以达到比开直槽更佳的降耗效果。

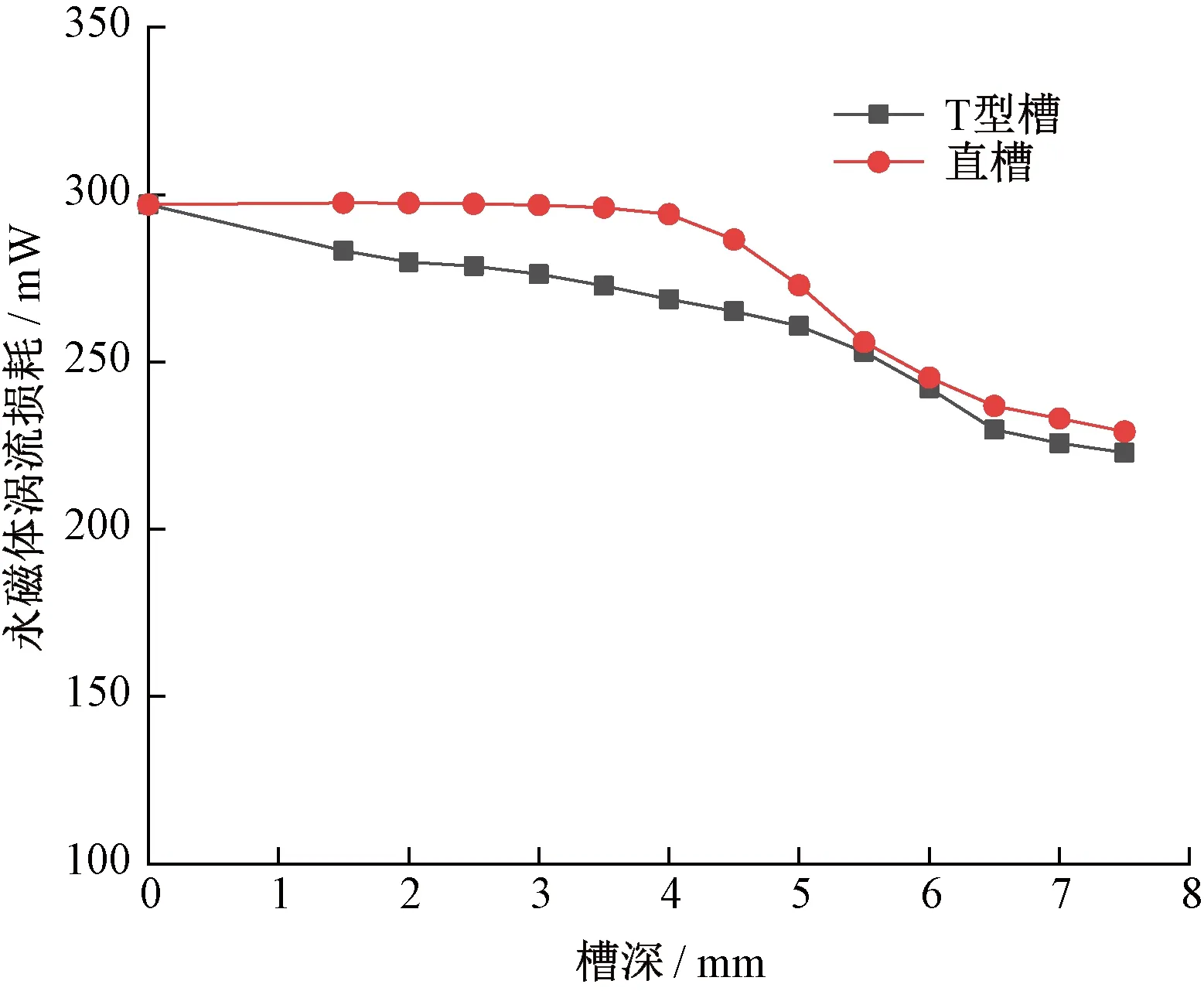
图10 槽深对永磁体涡流损耗的影响Fig.10 Influence of slot depth on magnet eddy loss

4 电机尺寸优化设计

为了在开T型槽的转子结构中放置固定装置，需要将永磁体改为不等厚结构，即永磁体偏心距H>0。不等厚磁极的转子结构如图11所示。

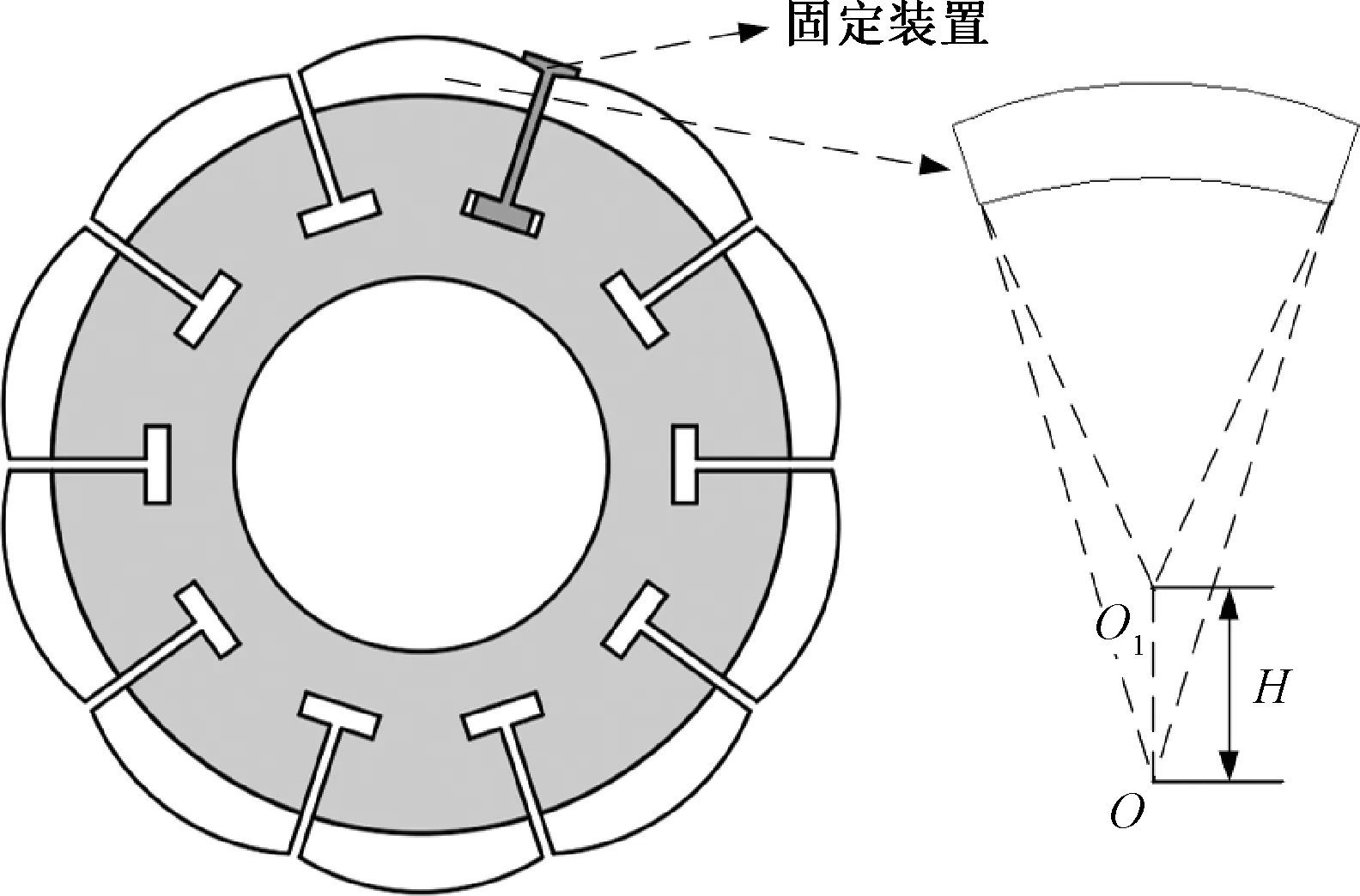
图11 不等厚磁极的转子结构Fig.11 Rotor structure with unequal thickness poles

通过对永磁体极弧系数的分析可知，不等厚永磁体两侧体积减小时，永磁体的极弧系数减小，随之永磁体涡流损耗和电机额定转矩减小。为了在降低永磁体涡流损耗和解决固定问题的同时，将对电机额定转矩的影响降至最小，考虑对电机结构进行多目标优化。多目标优化问题的数学描述为

(5)

式中：X为需要优化的一组设计变量，X=(x1,x2,…,xn)T；f(X)为一组目标函数，f(X)=[f1(X),f2(X),…,fk(X)]T；g(X)为一组约束条件，g(X)=[g1(X),g2(X),…,gm(X)]T。

设计变量包括定子槽口宽度、定子槽口高度、永磁体偏心距和T型槽深，其取值范围如表2所示。设计变量的取值范围即优化问题的约束条件，如定子槽口宽度需考虑绕组下线的要求，永磁体偏心距需满足放置固定结构的要求。在电机多目标优化问题中，目标函数一般为电机的重要性能参数，这些性能参数与设计变量之间存在复杂的函数关系。本文中电机优化目标的选择同时兼顾了电机的输出性能和损耗性能，因此选择电机额定转矩、转矩脉动系数及永磁体涡流损耗作为优化目标。

表2 设计变量及其取值范围Table 2 Design variables and their value ranges

电机优化过程在Ansys Workbench平台上使用Maxwell和optiSLang联合进行，利用optiSLang中提供的优化算法工具包对电机进行多目标优化，优化算法为粒子群优化(particle swarm optimization, PSO)算法，PSO算法通过对粒子群中微粒速度和位置进行不断更新和迭代，从而寻找粒子群的全局最优解[16]。微粒第k+1次迭代的速度和位置可表示为

Vk+1=ωVk+C1ξ(Pi，k-Xk)+C2η(Pg，k-Xk)

(6)

Xk+1=Xk+Vk+1

(7)

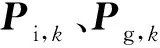
在PSO算法寻优过程中，每个微粒当前位置对应的适应度(目标函数值)通过在Maxwell中设置电机的设计参数计算求得。考虑到优化问题的规模，将PSO算法的初始种群数和最大迭代次数分别设置为10和200。

电机的多目标优化问题不存在唯一的最优解，最终得到的是一组Pareto最优解，从中选择一个合适的方案进行仿真验证。利用有限元软件计算得到电机优化后的电机额定转矩和永磁体涡流损耗如图12和表3所示。由表3可知：电机永磁体涡流损耗从298 mW下降为211 mW，下降了29%；而电机额定转矩从681 mN·m下降为679 mN·m，下降幅度可以忽略不计；转矩脉动系数表征电机瞬时输出转矩的波动性，转矩脉动系数从3.5%下降为1.6%，表明输出转矩稳定性得到进一步提高。

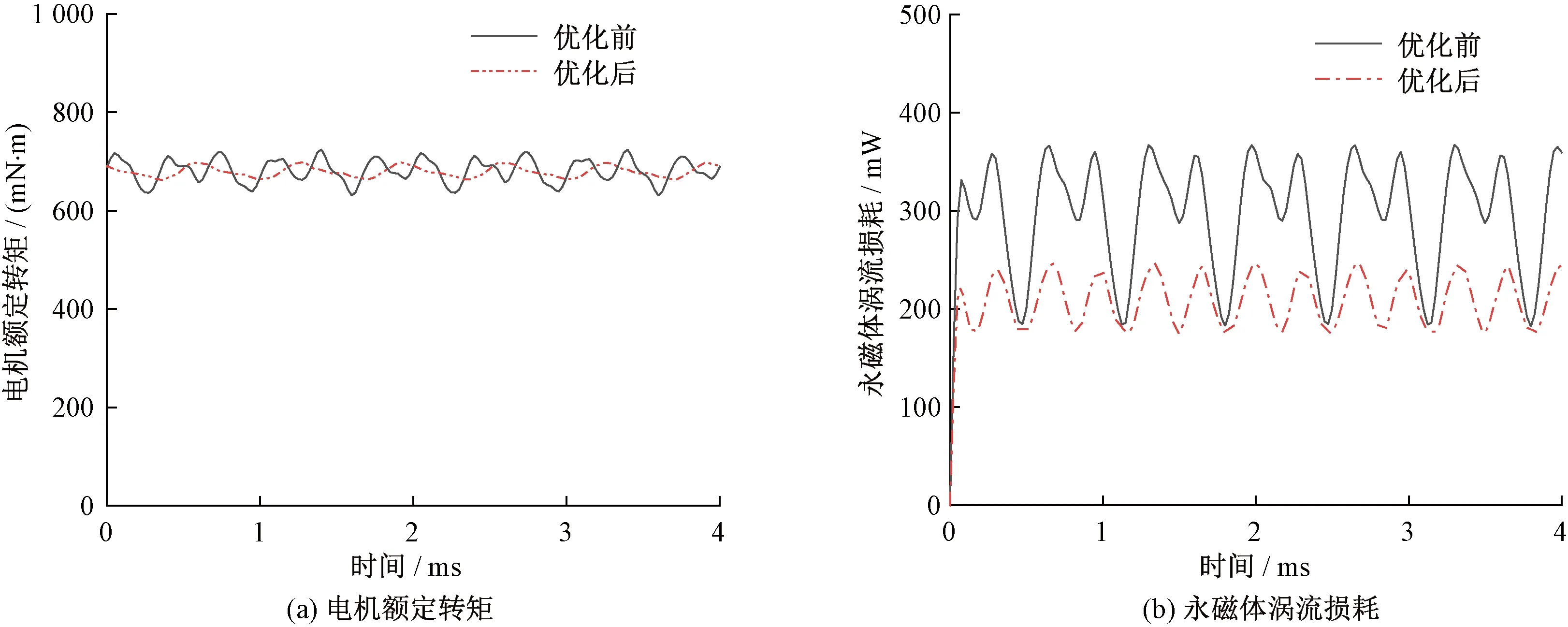
图12 优化前后电机额定转矩和永磁体涡流损耗的变化Fig.12 Changes of motor rated torque and permanent magnet eddy current loss before and after optimization

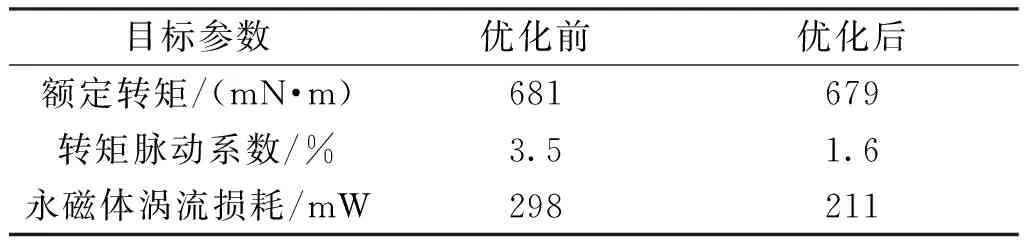
表3 优化前后目标参数的变化

5 结 语

利用有限元仿真软件Maxwell建立了表贴式永磁交流伺服电机模型，探究了永磁体极弧系数变化和转子q轴开T型槽对永磁体涡流损耗的影响。结果表明：永磁体电角度θ>120°时，单位永磁体电角度的增加对永磁体涡流损耗的贡献大于对电机额定转矩的贡献，且趋势在逐渐增强，因此选择在转子q轴位置开槽对电机额定转矩的影响最小；转子q轴开T型槽能够削弱7、13阶次谐波磁场，从而降低涡流损耗，且与直槽相比，能够拓展开槽空间；多目标优化后，电机的永磁体涡流损耗下降了29%，电机额定转矩没有明显下降，同时T型槽结构可以安放永磁体固定装置，解决了表贴式永磁体的安装问题。