基于行驶数据挖掘的DCT车辆平直道路换挡规律研究*
秦大同,王 康,冯继豪,刘永刚
(重庆大学,机械传动国家重点实验室,重庆 400044)
前言
换挡策略对车辆动力性和经济性等性能的影响较大[1],目前国内外学者对自动变速车辆的换挡策略进行了深入研究,主要分为两类:基于车辆动力学制定换挡规律和基于智能算法训练挡位决策模型。基于车辆动力学制定换挡规律,一般通过建立目标车辆动力学模型,在动力性等约束条件下,利用解析法等求取换挡规律,但该方法对不同行驶工况和驾驶风格的适应性差。文献[2]和文献[3]中通过优化特定工况下的换挡规律来提升其适应性。其中Song等[2]通过识别上下坡工况并修正该工况下的换挡规律,使车辆对该工况有较好的适应性。文献[4]和文献[5]中通过动态规划算法在给定约束下求取已知工况的最佳换挡规律。但该类方法在实车应用过程中,为提升车辆综合性能还须耗费大量人力物力在各类工况下做人工标定,且制定完成的换挡规律很难再更新。
基于智能算法训练挡位决策模型,一般通过考虑驾驶风格、驾驶意图和行驶工况的影响,利用支持向量机等智能算法学习熟练驾驶员的换挡策略,再通过训练好的模型控制变速器换挡。张元侠[1]通过多维数据识别行驶工况,再利用支持向量机训练挡位决策模型,并验证该挡位决策模型的合理性。陈清洪等[6]利用动态模糊神经网络拟合驾驶员换挡点进而控制换挡。该类方法可较好学习熟练驾驶员的换挡策略,适应性也较强,是挡位决策智能化的一个重要发展方向。但该类方法使用的智能算法计算量大,须装备高性能计算芯片,目前无法大量应用于实车。
鉴于上述研究的不足,本文中结合两类方法的长处,提出了一种通过挖掘海量行驶数据制定换挡规律的方法。首先,设计试验采集熟练驾驶员驾车行驶数据,再通过数据的清洗、集成与特征拓展和平直道路数据的筛选、特征提取、离群点去除与数据标准化来提取影响平直道路换挡策略的3个最主要特征的标准化数据,然后通过对各挡位下决策值分类精度最高的随机森林算法生成三参数换挡规律。通过挖掘熟练驾驶员在平直道路上驾车行驶数据中的换挡策略来制定换挡规律,可将熟练驾驶员对车况和道路工况等的综合考量融入换挡规律中,并增强其工况适应性,避免了复杂的人-车-路建模和人工标定过程,缩减了开发周期;通过将训练过的挡位决策模型转换为换挡规律,使该方法可直接应用于实际车辆。
1 数据采集
为使数据挖掘结果更具实用性,设计了实车道路数据采集试验。为避免不同驾驶风格对换挡策略挖掘的影响,按文献[7]中的方法,选择20位驾驶风格为“标准型”的熟练驾驶员进行数据采集试验,其驾龄都超过2年,平均驾龄为8.6年。假设数据采集试验中熟练驾驶员的换挡策略为最佳换挡策略,不对其换挡策略根据最佳经济性等指标进行筛选或修正。
试验车为某型装备7挡DCT变速器的SUV,通过车辆OBD接口和Vehicle Recorder数据采集设备读取行驶数据,如图1所示。

图1 试验车辆与数据采集设备
为保证采集数据更全面和更接近实际行驶环境,在重庆市公路交通网中选取了一段包含市区道路、城郊道路、山路和快速路的行驶路线,路线总长约为100 km,如图2所示。
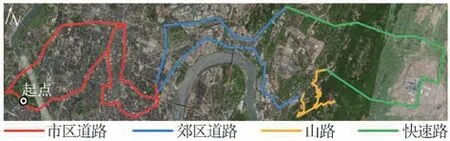
图2 数据采集试验行驶路线
在确认驾驶员适应试验车操作特性后,开始试验,最终共采集109.88 h行驶数据。采集数据包括实际挡位、目标挡位、转向盘转角、车速、纵向加速度、制动油压、节气门开度、加速踏板位置、发动机转速和发动机转矩等。因为采集的数据来源于多个传感器,其时序信息不一致,且部分数据存在噪声和缺失值,故须进行数据预处理,以便后续对换挡规律的挖掘。
2 数据预处理
图3为本文挖掘的平直道路下熟练驾驶员换挡策略方法的整体结构框图。数据预处理部分主要包括数据清洗与集成、特征拓展与数据筛选、主要特征提取、离群点去除和数据标准化。
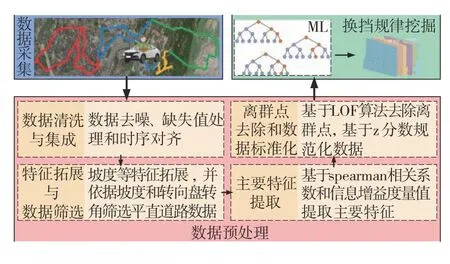
图3 换挡规律挖掘方法结构框图
2.1 数据清洗与集成
由于CAN通信偶发性丢包等因素会导致部分数据缺失,故须进行缺失值处理。经检测发现纵向加速度数据存在少量缺失值,且系统用“-16”表示该缺失值,如图4(a)所示。缺失值的处理方法可分为删除和填充两类。纵向加速度数据中缺失值一般单个出现,若直接删除会影响后续数据处理,因此本文通过区域中心度量来填充该缺失值,处理结果见图4(b)。
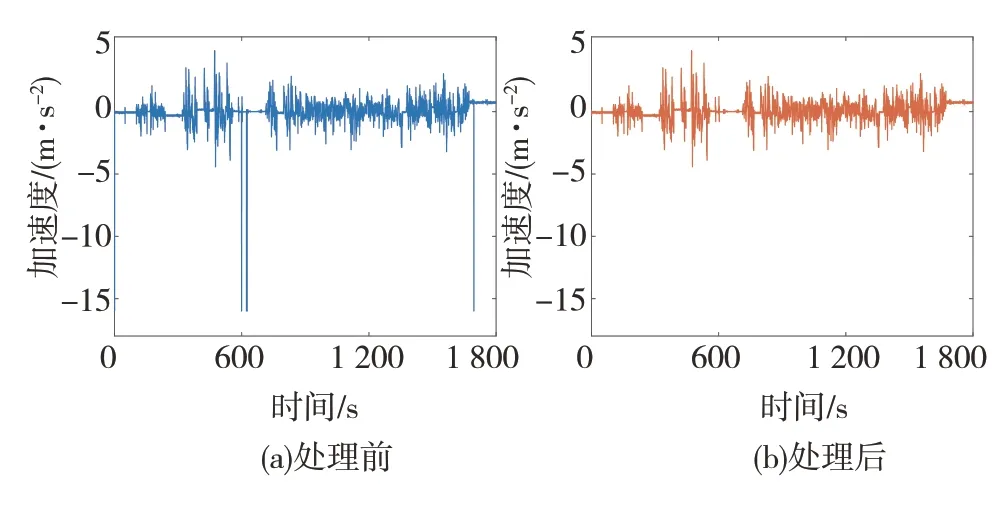
图4 异常值处理
车身振动等因素会导致采集数据包含噪声,本文采集数据中存在噪声的数据有:车速、纵向加速度、制动油压和发动机转矩。因为存在噪声的特征占比较大,如不进行去噪处理,将会严重影响数据挖掘效果。为此,利用去噪效果较好的小波去噪算法对4个含噪声特征进行去噪处理,阈值函数选择硬阈值。因为4个特征的频谱特性不同,故针对该4个特征采用的小波基函数分别为:sym3、haar、sym3、db6,分解层数分别为4、3、4、4,处理结果见图5。
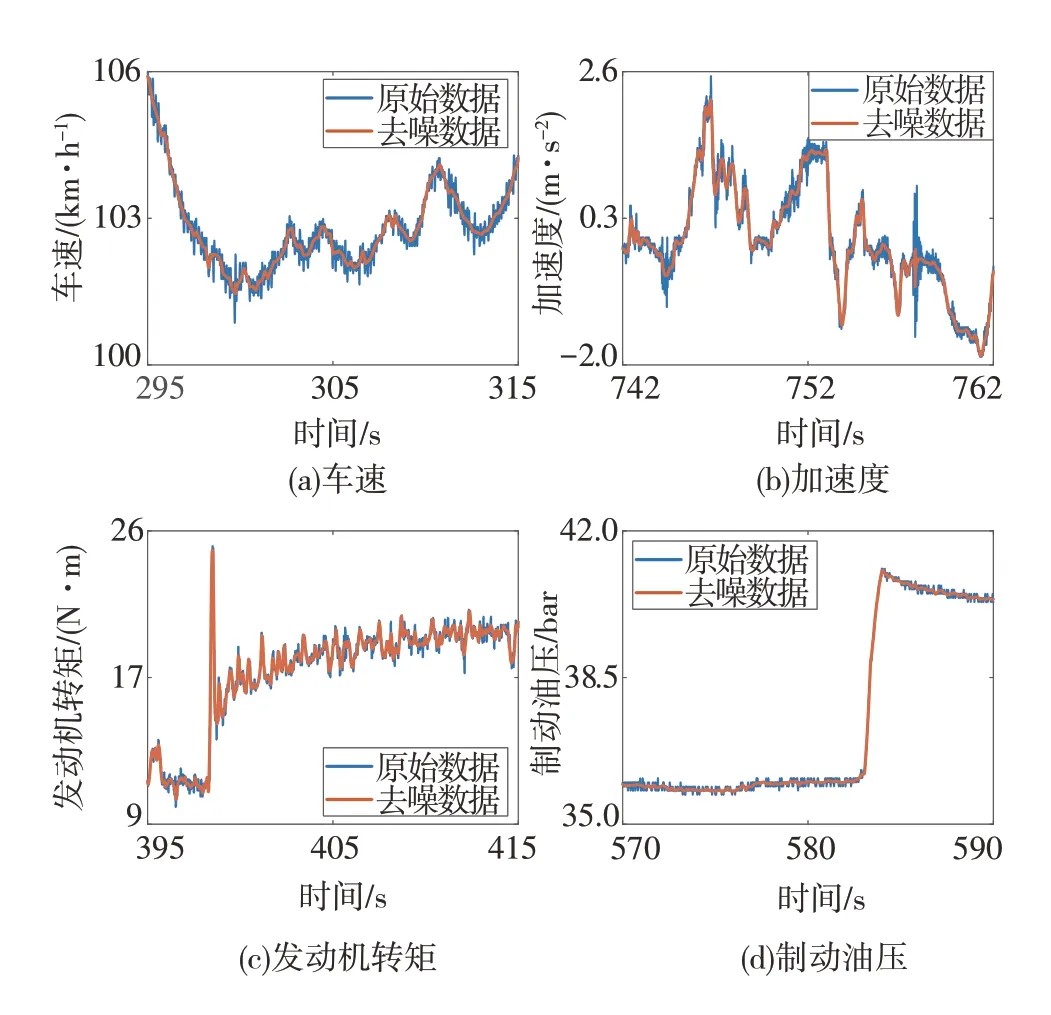
图5 去噪处理结果
表1为各特征采样频率和采样精度。由表可知,由于涉及多个传感器,各特征的采样频率和时序信息不统一。如果时序信息不能保证一致,则无法同时分析多个特征,数据挖掘效果也会变差,因此须进行频率统一和时序对齐处理。该处理一般采用插值的方法,为保证处理后的数据不失真,本文采用样条插值算法,并以车速的采样频率和时序信息作为基准。
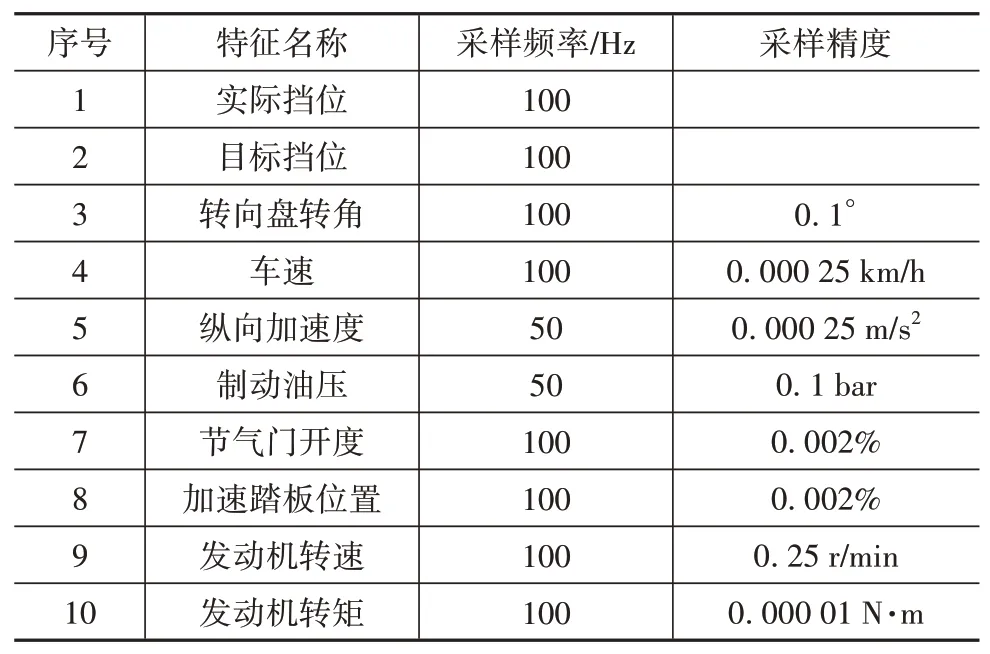
表1 各特征采样频率和采样精度
2.2 特征拓展与数据筛选
通过车载传感器采集的数据还不够全面,可能遗漏对于换挡规律挖掘非常重要的信息,例如挖掘平直道路换挡规律还需要道路坡度数据。因此须通过已有数据拓展出较为全面的特征组合。本文根据文献[8]中提出的方法,由实际挡位、车速、纵向加速度、发动机转矩和实车参数估计道路坡度(road slope,RS;序号:11),再由部分特征对时间求导来拓展特征,如表2和图6所示。
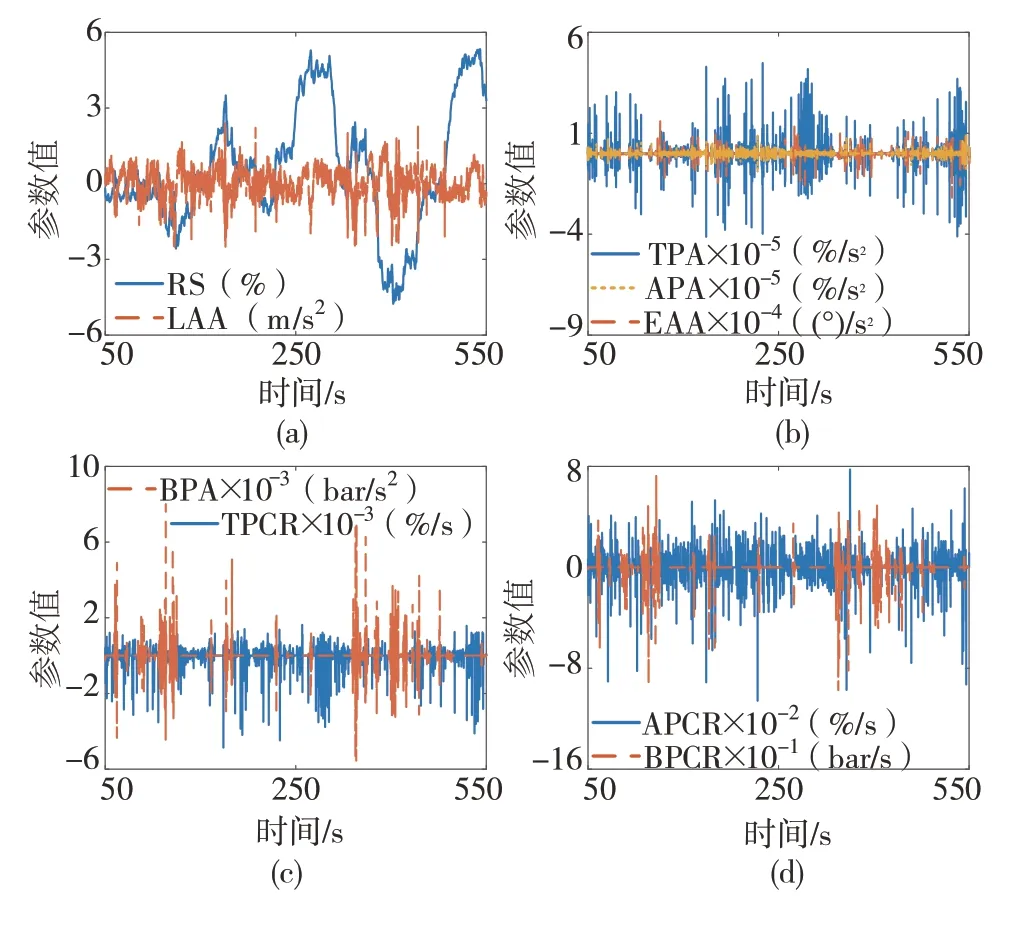
图6 拓展特征部分展示
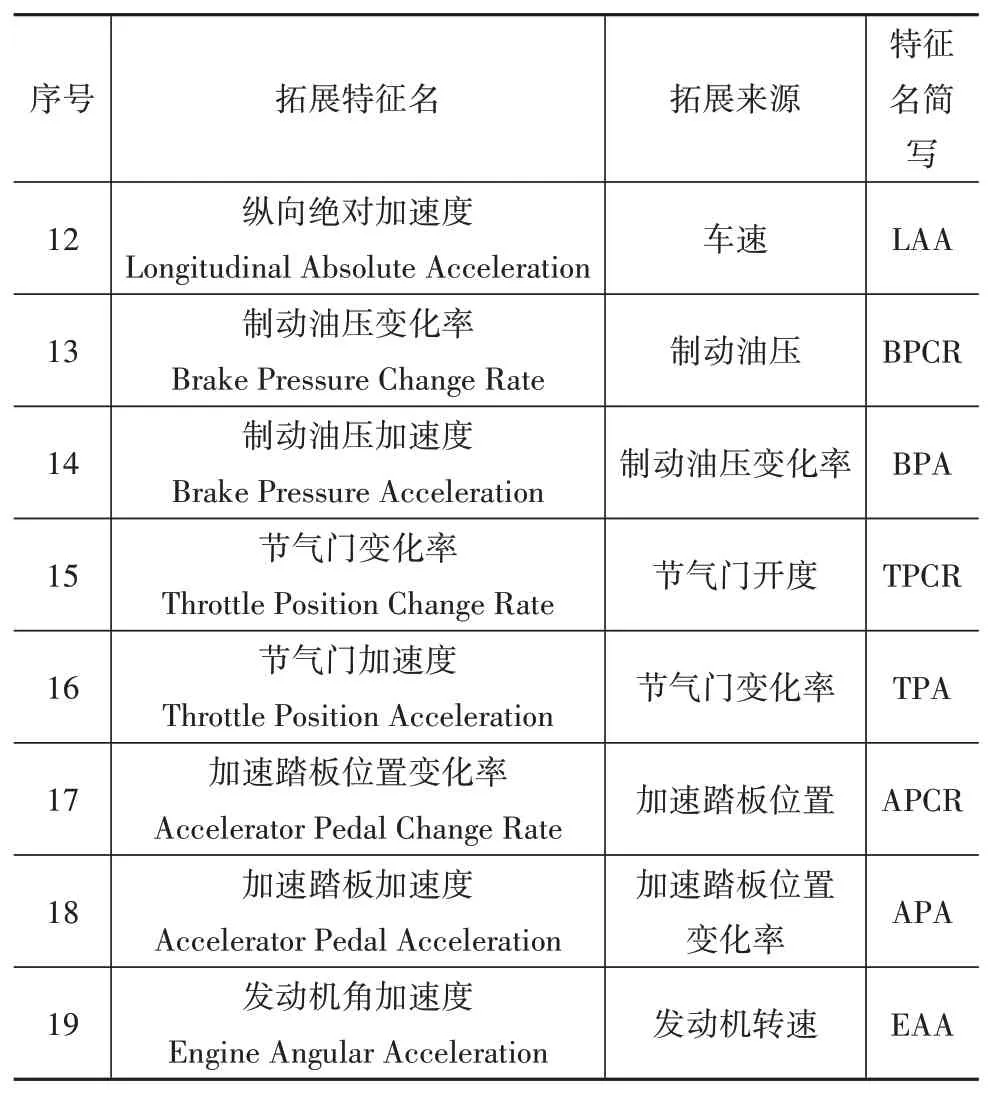
表2 特征拓展
文中所述平直道路工况是指车辆水平直线行驶工况,且试验车厂商提供的参数中转向盘自由行程为18°,同时试验车在水平地面行驶时,估计的坡度值在±2%范围内波动,此外停车工况无关挡位决策。因此提取车速大于0,且转向盘转角在±18°范围内,同时坡度在±2%范围内的数据点作为平直道路工况的数据点。
2.3 主要特征提取
本文最终目标是提取三参数换挡曲面,因此须提取影响换挡策略的3个最主要特征,为避免冗余特征干扰,在特征重要性分析前须去除冗余特征[9]。上述19个特征中,实际挡位和目标挡位属于标签特征,转向盘转角和坡度属于筛选特征,纵向加速度是车载加速度计测得的不包含重力加速度分量的相对加速度,且已由车速拓展成纵向绝对加速度,所以先去除该5个特征。为进一步去除冗余特征,还须分析剩余14个特征的相关性。经Kolmogorov-Smirnov检验,14个特征都不符合正态分布,故通过spearman相关系数分析14个特征彼此间的相关性,结果见表3。表3中车速、制动油压、节气门开度、加速踏板位置、发动机转速和发动机转矩的特征名分别简写为VS(vehicle speed)、BP(brake pressure)、TP(throttle position)、APP(accelerator pedal position)、ES(engine speed)和ET(engine torque)。
spearman相关系数绝对值大于0.6表明特征间有强关联性[10]。为得到关联性最小的特征组合,对比表3中相关系数值,将节气门开度、发动机转速、发动机转矩和纵向绝对加速度去除。冗余特征去除后,剩余10个特征,为筛选出3个最主要特征,还须进行特征重要性分析。
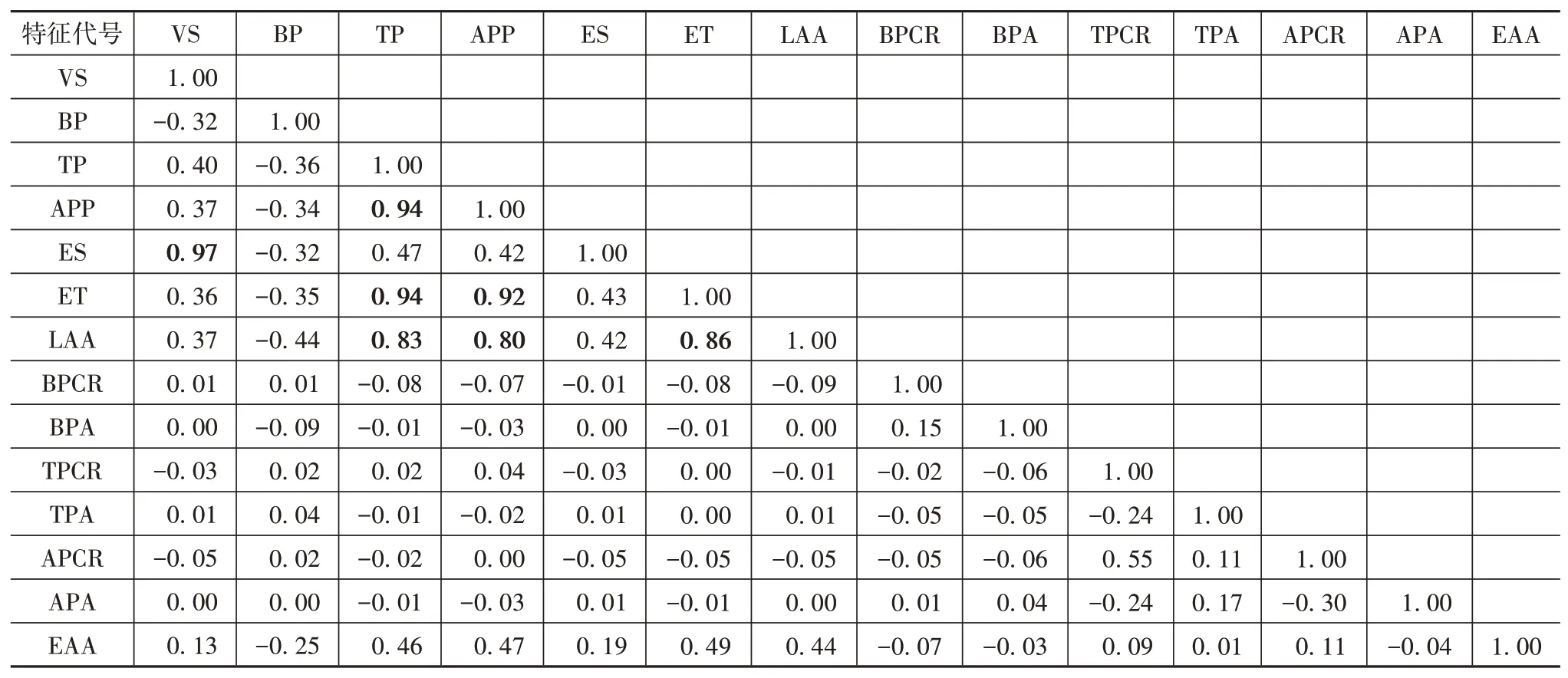
表3 特征间spearman相关系数
文中将换挡规律挖掘转换为每个挡位下的升降挡和保持的分类问题,降低了分类难度,有效提高了分类精度,但也须为每个挡位建立一个分类模型,以对每个挡位分别进行特征重要性分析。通过可评价分类效果的信息增益度量来衡量各特征的重要性:
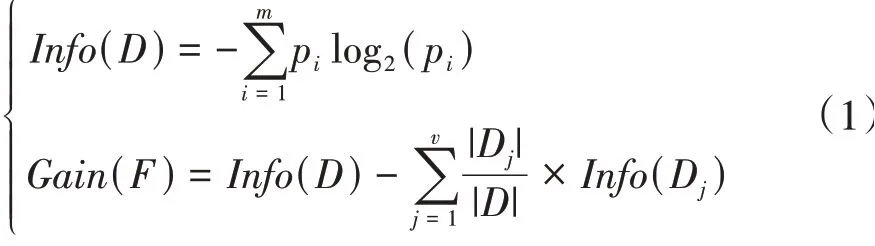
式中:D表示某一分组;m为类的总数;pi为D中任一数据属于i类的非零概率;F表示某一特征;v表示D子分组的个数。结果见表4。
表4中各挡位下车速、加速踏板位置、发动机角加速度3个特征的重要性都排前三,且重要性之和最低为0.831。为降低换挡规律的复杂度和增强其实用性,将车速、加速踏板位置和发动机角加速度作为各挡位分类模型的辨识特征。
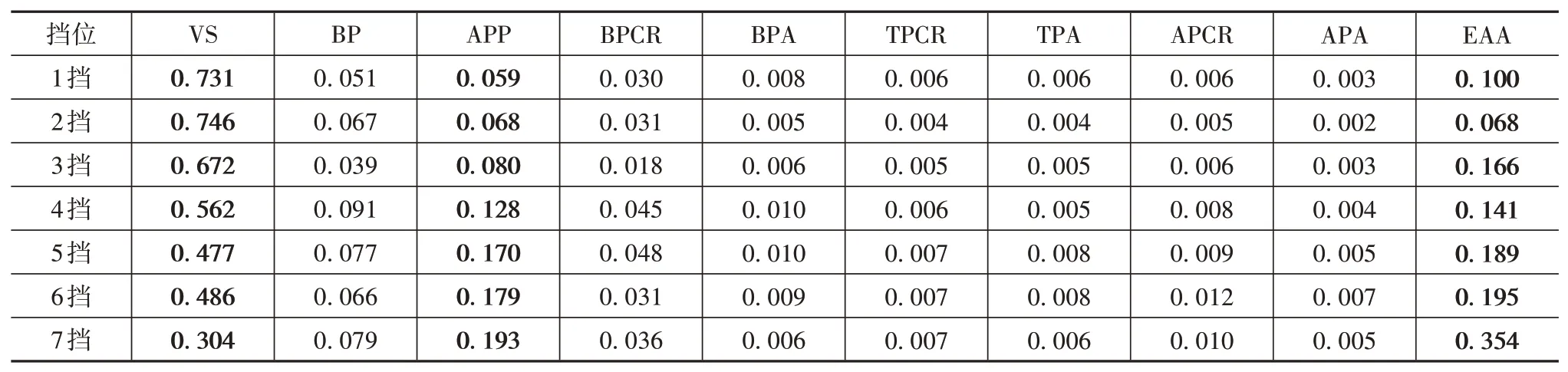
表4 各挡位下特征信息增益度量值
2.4 离群点去除与数据标准化
因为须对每个挡位下的升挡点、保持点和降挡点进行分类,但每个挡位数据中都存在离群点,而离群点的存在会影响分类精度,故须进行离群点去除。选择基于密度且不受数据分布影响的Local Outlier Factor算法对每个挡位的离群点进行检测和去除[11],各挡位下升挡点、保持点、降挡点和离群点分布见图7。
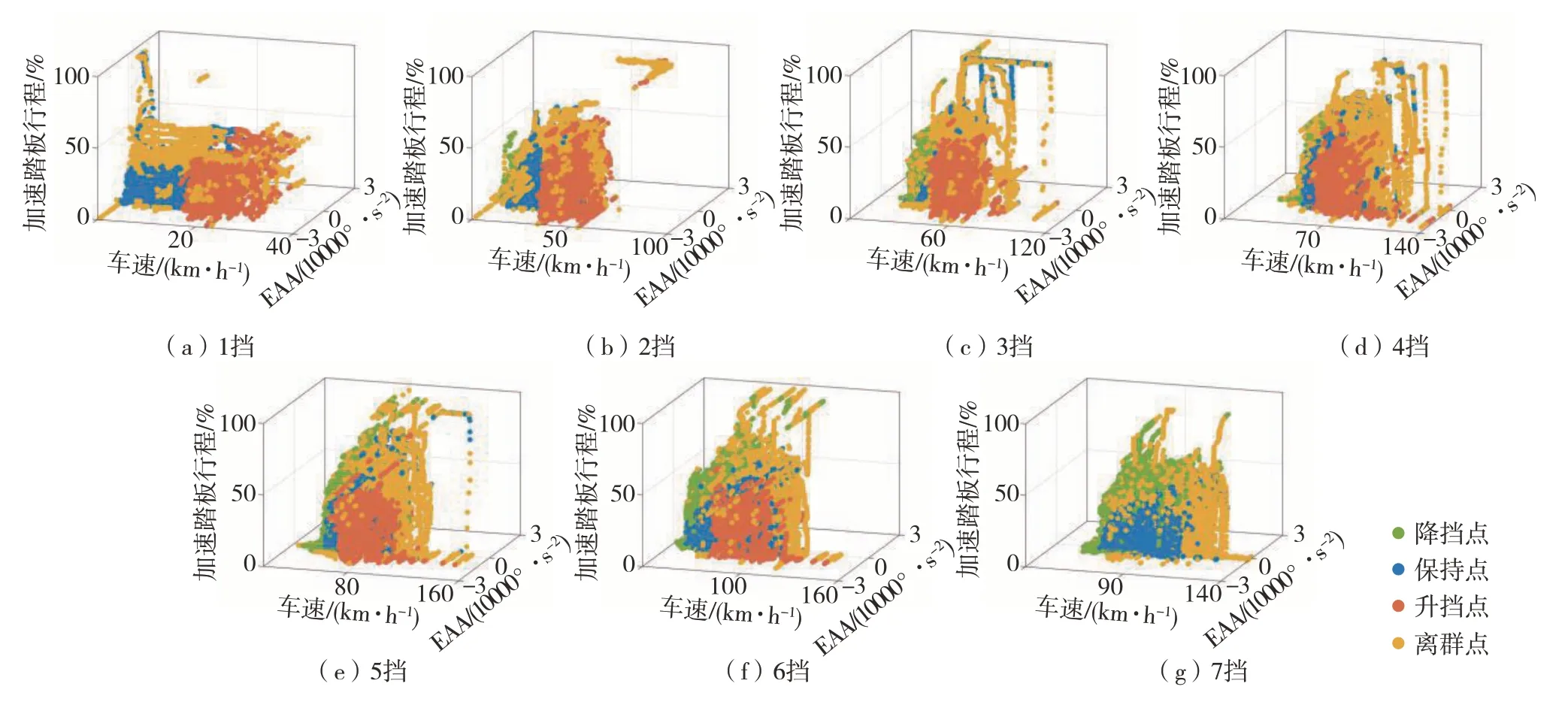
图7 各挡位下升挡点、降挡点、保持点和离群点分布
此外,由于最终选取的3个重要特征的量纲不同,为避免其对分类算法精度的影响,采用鲁棒性较好的均值绝对差z分数方法对各挡位数据进行标准化处理,其计算公式为

式中:x'i为标准化处理后的数据;xi为原始数据为x的均值;sA为均值绝对偏差。
数据预处理后,最终得到的各挡位数据点个数分别为350 958、812 092、942 934、856 130、889 210、942 720、1 067 440。其中1挡数据点明显少于其它挡位,经分析是因为转弯和爬坡一般在低挡位,而本文挖掘的是平直道路换挡规律,因此通过数据筛选,1挡的数据点较少。此外,行驶路线中有较多高速路或快速路,同时该工况下弯道和坡道较少,因此处理后的数据中高挡位数据较多。
3 换挡规律挖掘
在经过数据预处理得到的各挡位数据中,1挡数据有升挡和保持两类,7挡数据有保持和降挡两类,其余5挡数据有升挡、保持和降挡3类。因此须对7组数据分别训练分类模型,目前有监督学习中分类效果较好的算法:C4.5、逻辑回归、K最近邻、朴素贝叶斯、支持向量机和随机森林等[12]。其中C4.5算法易过拟合,逻辑回归算法和K最近邻算法在处理数据不平衡问题上效果较差。而本文处理的分类问题要求分类算法不能过拟合,否则会导致分类模型外延性差,且影响后续升降挡曲面的生成,同时原始数据集中升挡点和降挡点数量相对保持点较少,所以分类算法须克服数据不平衡问题[13]。因此本文采用朴素贝叶斯(naive Bayes,NB)、支持向量机(support vector machine,SVM)和随机森林(random forest,RF)3种分类算法分别对7组数据进行分类,其中SVM采用4种核函数,分别为linear核函数、polynomial核 函 数、RBF核函数和sigmoid核 函 数。之后通过10-折交叉验证的平均准确率比较各算法的分类精度,并筛选出效果最好的分类算法用于各挡位数据点的分类。各算法对决策值的分类精度见表5。
3.1 换挡策略学习
分类算法精度对比见表5。由表可知,6种分类算法在4挡、5挡和6挡的分类精度都稍低于其它挡位。对比表4可以发现,这是因为3个重要特征在4挡、5挡和6挡的重要性之和低于其它挡位,也即3个重要特征在4挡、5挡和6挡中对升挡、保持和降挡的区分能力稍弱。
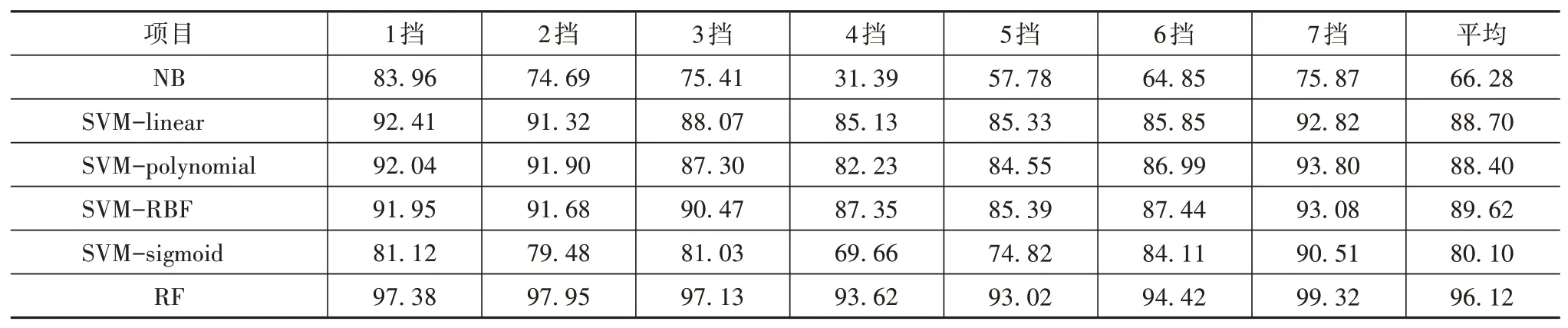
表5 分类算法精度对比 %
对比6种分类算法,其中NB的分类精度最差,RF最高,且RF在所有挡位的分类精度都超过了93%,平均分类精度更是达到了96.12%。图8为各挡位下RF混淆矩阵。在图8中,每个挡位下,“保持”的识别率最高,这是因为“保持”类数据点的占比很大,导致算法在追求总分类精度时牺牲了小类的识别率,但每个挡位的升挡和降挡识别率最低也达到83.50%,且大部分超过90%,与“保持”类识别率相近,这表明RF具有很强的抗数据不平衡能力,可以很好处理本文中的分类问题,因此采用RF对7个挡位分别建立分类模型。
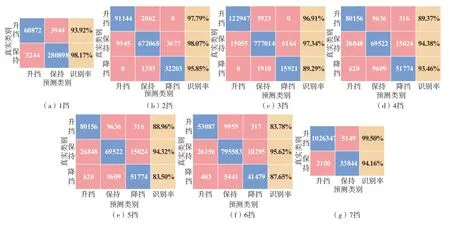
图8 各挡位下RF混淆矩阵
3.2 换挡规律提取
在提取换挡曲面时,先对由车速、加速踏板位置和发动机角加速度构成的三维空间按离散精度生成待分类点集,并通过训练好的分类模型对所有离散点进行分类,再分别提取升降挡点群的边界点生成换挡曲面。表4中各挡位下车速都很重要,因此将车速特征作为主特征,用另两个特征构成换挡曲面。因为升挡是从低速到高速,降挡是从高速到低速,所以将分类后的升挡点群在车速维度(车速值左小右大)的最左曲面作为升挡曲面,将降挡点群在车速维度的最右曲面作为降挡曲面。
根据图7中数据点分布情况,设置待分类空间中车速、加速踏板位置和发动机角加速度取值范围分别为0~160 km∕h、0~100%和-30 000°∕s2~30 000°∕s2。由发动机转速采样精度和采样时间得发动机角加速度精度为150°∕s2,而车速和加速踏板行程的精度分别为0.000 25 km∕h和0.002%,在考虑计算成本后,设置各特征离散精度分别为0.01 km∕h、0.01%和150°∕s2,则待分类点共有6.4×1010个,换挡曲面共有4×106个数据点。此外,在对各挡位数据点分类前要根据式(2)标准化数据,并在分类后将数据还原,最终提取的换挡规律见图9。
图9中换挡曲面并不光滑,这表明局部最优点被保留,且升降挡曲面都有随着加速踏板行程变大,对应车速变大的趋势,这与动力性换挡规律相似。此外,换挡曲面有交叉情况,但本文挖掘的是各挡位下升降挡换挡规律,生成的换挡规律也需逐级判断升降挡,因此换挡曲面交叉不影响挡位决策。
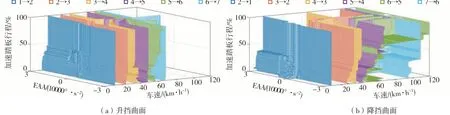
图9 数据挖掘换挡规律
4 仿真验证
为验证所挖掘换挡规律的实用性,同时考虑试验安全性,在Simulink环境中搭建模型并进行仿真验证。该仿真模型由驾驶员模型、车辆动力学模型和道路模型组成,其中驾驶员模型以PID控制为基础建立,车辆动力学模型由发动机模型、变速器模型和行驶阻力模型组成,道路模型由道路坡度和循环工况组成。其中车辆动力学模型中的各项参数采用试验车参数,如表6所示。
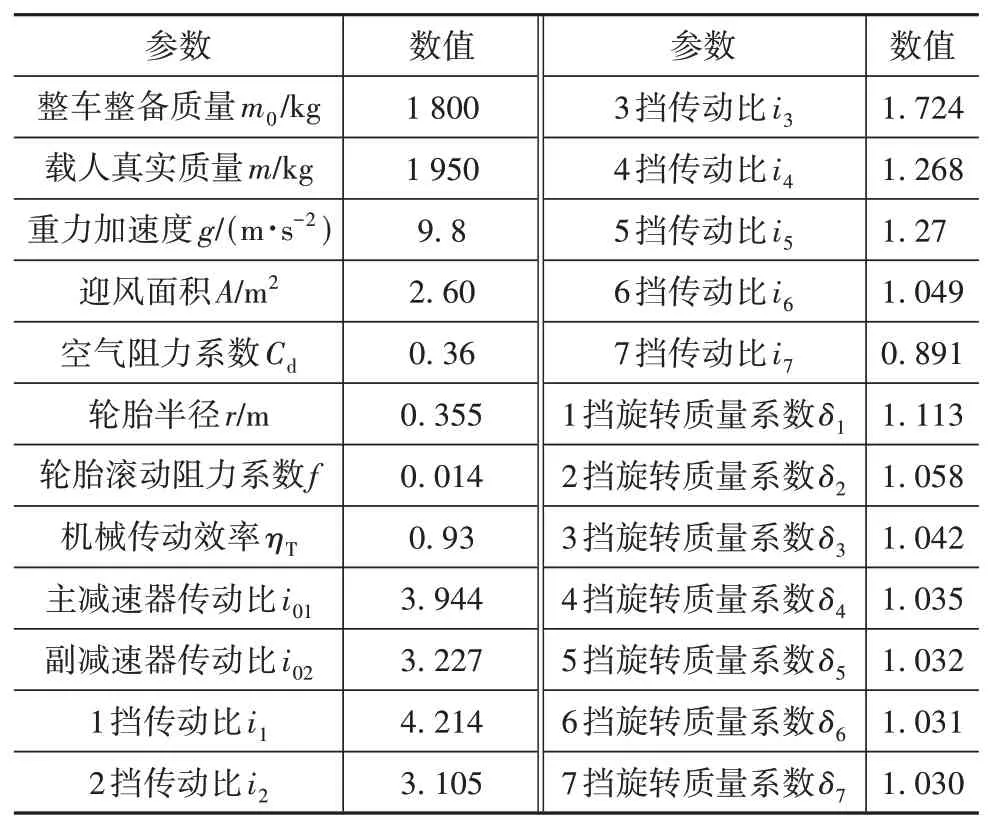
表6 实车参数
仿真验证中,通过文献[14]中的方法制定经济性换挡规律和动力性换挡规律,并与本文所挖掘的换挡规律作对比。仿真验证包含两个部分,第一部分是百公里加速仿真,主要对比动力性,第二部分是CLTC-P循环工况仿真,主要对比经济性和换挡次数。采用的CLTC-P循环工况为中国乘用车行驶工况,其累计里程为14 480 m,更接近国内乘用车驾驶实际情况,且包含数据采集试验中的城市工况、郊区工况和高速工况(分别对应图12中0-674、675-1 367和1 368-1 800 s工况),可全面检验所挖掘换挡规律的实用性。
此外,发动机角加速度很少出现绝对值大于30 000°∕s2的情况,且图9中的每个换挡曲面上,当发动机角加速度绝对值大于25 000°∕s2时,每一加速踏板位置下车速值基本不变,因此仿真中当发动机角加速度绝对值超过30 000°∕s2时,默认其绝对值为30 000°∕s2。
4.1 百公里加速仿真
百公里加速仿真中,驾驶员模型的加速踏板行程设置为100%,制动压力设置为0,转向盘转角设置为0,道路模型中道路坡度设置为0,不设置循环工况,仿真结果如图10和图11所示。
图10中数据挖掘换挡和经济性换挡的加速时间较动力性换挡分别超出17.52%和45.71%。且经济性换挡的换挡节奏最快,车速到100 km∕h时,其挡位为7挡,而数据挖掘换挡为4挡,动力性换挡为3挡,这也导致其动力性一直弱于其它两种换挡规律。此外,数据挖掘换挡的换挡趋势介于经济性换挡和动力性换挡之间,虽加速时间比动力性换挡多1.51 s,但其动力性较经济性换挡有明显提升。图11中因升挡时变速器传动比降低,发动机转速下降,导致换挡时发动机角加速度先下降后升高。
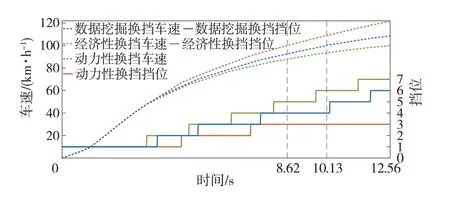
图10 百公里加速仿真结果
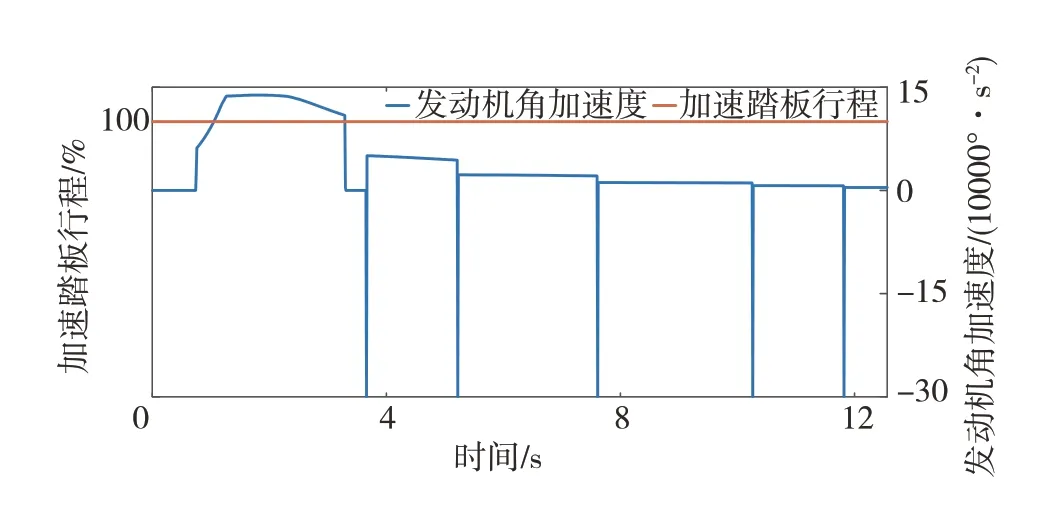
图11 百公里加速仿真中数据挖掘换挡相关参数
4.2 CLTC-P循环工况仿真
CLTC-P循环工况仿真中,驾驶员模型的转向盘转角设置为0,道路模型中道路坡度设置为0,循环工况设置为CLTC-P,仿真结果如表7、图12和图13所示。
表7表明,数据挖掘换挡油耗接近经济性换挡,且动力性换挡油耗较大。图12中经济性换挡节奏同样很快,而动力性换挡节奏较迟缓,表7中换挡次数数据也体现了这一点。同时,经济性换挡为追求经济性经常出现低速高挡位的情况,虽有效降低了油耗,但换挡次数较另两种换挡规律猛增。不过经济性换挡在高速工况中能跟随车速的变化及时换挡,更适应该工况,而动力性换挡更适应城市工况,其换挡次数少,在城市工况中可避免频繁换挡,但在另两个工况中则会出现延迟升挡的情况,相比于动力性∕经济性换挡,数据挖掘换挡则始终能根据车速变化情况及时调整挡位,对城市工况、郊区工况和高速工况都有较强的适应性。动力性换挡虽在换挡次数方面表现较好,但这只是其延迟升挡带来的好处,而缺点则是平均油耗较经济性换挡增加了20.66%。与经济性换挡相比,数据挖掘换挡规律,在平均油耗微增0.89%情况下,换挡次数大幅减少了63.33%,在保证较强经济性的同时也减少了变速器的磨损。
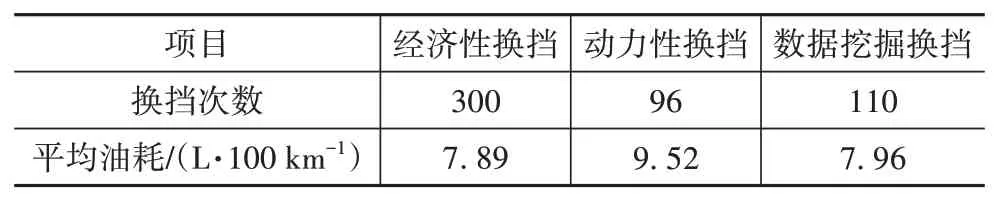
表7 换挡次数和平均油耗
由图12和图13可见,数据挖掘换挡规律具有较强的实用性,即更接近经济性换挡规律,经济性较好,但其动力性比经济性换挡也有较大提升,较动力性换挡也未大幅下降。总的来说,数据挖掘换挡规律在保持较低油耗的同时,显著提高了车辆动力性,减少了换挡次数,在经济性和动力性间有较好平衡,综合性能较好,这验证了本文所提方法对熟练驾驶员换挡策略的有效挖掘,也验证了所挖掘换挡规律的实用性。
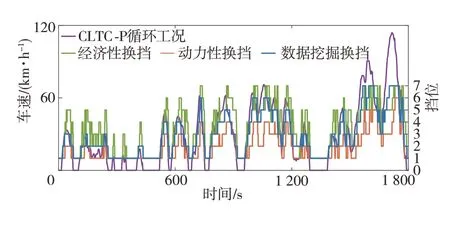
图12 CLTC-P循环工况仿真结果
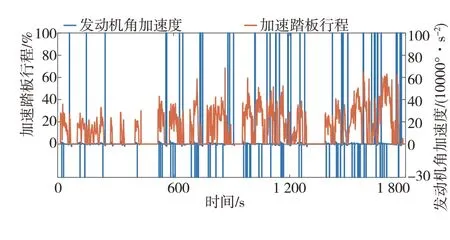
图13 CLTC-P循环工况仿真中数据挖掘换挡相关参数
此外,经在CPU为i5-9400F∕2.9 GHz、内存为16 G∕2400 MHz的计算机上测试,由随机森林算法训练的挡位决策模型预测一次挡位的平均用时为1.38×10-4ms,而由三参数换挡规律查询一次挡位的平均用时为3.8×10-5ms,下降了72.46%,明显降低了计算量。且现有变速器控制芯片的计算性能远不如上述计算机,因此基于智能算法的挡位决策模型无法广泛用于现有实车。而由本文方法制定的三参数换挡规律数表不需要高性能芯片,可通过替换现有变速器换挡规律数表直接应用于实车,普适性更好。
5 结论
针对目前自动变速车辆挡位决策方法对环境适应性差或难以直接应用于实车的问题,本文通过挖掘熟练驾驶员驾车行驶数据来提取平直道路三参数换挡规律。首先通过数据预处理从试验采集数据中提取出平直道路工况下3个最重要特征(车速、加速踏板位置和发动机角加速度)的标准化数据,然后比较6种机器学习算法对各挡位下3种决策值的分类效果,选用效果最好的随机森林算法提取各挡位下换挡规律。仿真结果表明,该方法普适性好,能有效提取熟练驾驶员换挡策略,提取的换挡规律适应性较好,在保证较好经济性的同时,也具有较好的动力性,且换挡次数较少,综合性能好。

