共晶Ga-Sn与10Li-GaSn的第一原理分子动力学研究

丁安，王建川

共晶Ga-Sn与10Li-GaSn的第一原理分子动力学研究

丁安，王建川

(中南大学 粉末冶金国家重点实验室，长沙 410083)

液态共晶Ga91.6Sn8.4可作为锂离子电池的负极。本文采用第一原理分子动力学方法对Ga91.6Sn8.4和嵌锂10%(摩尔分数，%，下同)的Ga91.6Sn8.4(10Li-Ga91.6Sn8.4)的结构和动力学特性进行对比分析。结果表明，Ga91.6Sn8.4与10Li-Ga91.6Sn8.4在结构上没有明显差异，为短程有序，但Li的嵌入使得10Li-Ga91.6Sn8.4径向分布函数的第二峰出现“劈裂”，表明体系有序度增加，熔化温度提高。10Li-Ga91.6Sn8.4中，Li的嵌入使得体系中各原子的扩散系数减小，Li-Sn原子间相互吸引力明显强于Li-Ga，充电过程中，Ga91.6Sn8.4液态金属锂离子电池呈现液体向固体转变的趋势。

Li-Ga-Sn体系；第一原理分子动力学；液态结构；扩散系数；黏度

随着传统能源的匮乏和环境的日益恶化，液态金属作为一种新型的电化学储能技术逐渐走进人们的视野[1]。液态金属的流动特性可以从本质上解决电池中枝晶生长问题，同时液相中更快的原子迁移有利于提高传质动力学过程[2]。除此以外，液态金属电池可以通过密度差自动分离为三层，其中密度较低的液态金属负极位于顶层，中间是熔融盐电解质，最底层是正极。放电时，负极失去电子被氧化，厚度减小，充电过程则相反[3]。因此，液态金属锂离子电池相比于传统的固态锂离子电池，制造成本显著降低，电化学性能提高。由于Ga的熔点低，室温下呈液态且无毒，在低于熔点的温度，还表现出强烈的过冷倾向，近年来，许多学者将Ga基液态金属及其合金作为锂离子电池的负极。进一步研究表明，少量Sn或In加入Ga中，不仅可以增加锂离子电池的容量，还可以降低熔点(Ga的熔点为302.8 K，共晶Ga91.6Sn8.4的熔点为293.9 K，共晶Ga75.5In24.5的熔点为288.7 K[4])。关于液态Ga基锂离子电池，DESHPANDE[5]曾在313 K条件下展现了电池的自愈合过程，发现该电池在锂化过程中，每个Ga原子可以结合2个Li原子，形成Li2Ga合金，理论容量达到769 mA·h/g，同时，液态金属电极的自愈合特性也显著提升了电池的耐久性能。WU等[6]采用Ga-Sn作为锂离子液态金属电池的自修复负极，将液态合金固定在氧化还原石墨烯和碳纳米管形成的骨架中，以防止Ga-Sn纳米粒子在循环过程中聚集或分离，电化学测试结果表明该电池具有795 mA·h/g的理论容量，且在4 000次循环下容量几乎没有任何损失。液态金属与常见的晶体不同，液态缺乏长程有序结构，其结构信息对于分析材料的物理化学性质至关重要。2018年，ZHAO等[7]利用X射线衍射光谱对共晶Ga91.6Sn8.4熔体内的团簇结构进行解剖，结果表明，中心原子周围均有10个Ga原子和2个Sn原子，在以Sn原子为中心的团簇中，这2个Sn原子之间相互作用较强，并倾向于聚集。

第一性原理分子动力学模拟已被广泛应用于研究液相结构和动力学特性[8]。基于共晶Ga-Sn在电池领域的应用，目前实验上主要致力于对其表面形貌以及电化学性能展开广泛研究，而对其微观层面上嵌锂过程的认识鲜有报道。本文采用第一性原理分子动力学方法研究室温下少量Li的嵌入对液态共晶Ga-Sn基体结构的影响，并在此基础上给出各原子的扩散系数，从而达到从微观层面上理解液态金属电池充放电过程的目的。

1 计算方法

采用Vienna从头算模拟软件包[9−10](vienna ab initio simulation package，VASP)对Li-Ga-Sn体系进行第一性原理分子动力学模拟。模拟过程考虑两个成分：共晶Ga91.6Sn8.4和10Li-Ga91.6Sn8.4(即Li的摩尔分数为10%，剩下的Ga, Sn保持共晶比例)。模拟在正则系综中进行，使用Nosé-Hoover恒温器控制温度[11]，价电子与原子核之间的相互作用由投影缀加波(projector augmented-wave, PAW)描述，将PBE(perdew-burke- ernzerhof)形式的广义梯度近似(general gradient approximation, GGA)用于交换相关能量泛函[12]，电子波函数用能量截止值为400 eV的平面波展开。采用考虑周期性边界条件的立方盒子，模拟温度为300 K，总原子数为200，初始构型为原子在晶胞中随机均匀分布，而晶胞的大小是通过控制外压在0 kB(1 kB=1×108Pa)附近得到。粒子的运动方程采用Verlet算法求解，时间步长为2×10−15s，每个系统的模拟时间为28×10−12s。所计算的径向分布函数以及扩散系数都是先通过6×10−12s的预平衡时间再统计剩下的5 500个平衡构型而得到。由于模拟的晶胞足够大，只考虑对布里渊区的Γ点进行采样。模拟体系的原子比例，摩尔体积0以及平均外压汇总列于表1。

表1 300 K下Ga91.6Sn8.4和10Li-Ga91.6Sn8.4的原子摩尔分数，摩尔体积(Vm)和平均外压(P)

2 结果与讨论

2.1 液相密度及混合焓

通过预留足够长的平衡时间，模拟得到的密度以及混合焓列于表2。混合焓作为热力学中需要考虑的基本物理量之一，可以通过下式计算：

式中：Δmix为混合焓，kJ/mol；(AB)，(A)和(B)分别代表在一定温度下合金AB, 相A和相B的自由能，kJ/mol；与分别是相A与相B的摩尔分数，%。

从表中可以看出，对于共晶Ga91.6Sn8.4，计算的密度和混合焓在数值上都与实验值吻合，误差在6%以内。其中，Li的引入使得Ga91.6Sn8.4密度减小，这主要是因为单质Li的密度仅为0.5 g/cm3，对体系密度的变化趋势起决定作用[15]。值得注意的是，共晶Ga91.6Sn8.4混合焓的计算值及实验值均为正值，说明相比于液态Ga和液态Sn，液态Ga91.6Sn8.4有液相分离的趋势。另外，Li的引入使得体系的混合焓也由原来的正值变为负值，表明液态Ga91.6Sn8.4嵌锂(即充电)时放热。对于Li-Ga-Sn体系，GANCARE等[16]通过实验测得1 081 K下Ga85Sn15中加入10%Li的液相混合焓为−5.22 kJ/mol，由于Ga91.6Sn8.4和Ga85Sn15的Δ差距很小(Ga85Sn15在803 K下的Δ=0.47 kJ/mol[14])，这表明Ga91.6Sn8.4中加入10%Li的混合焓也应在−5.22 kJ/mol附近，进一步证实本实验数据的可信度。

表2 Ga91.6Sn8.4和10Li-Ga91.6Sn8.4在300 K下的密度和混合焓(括号内为实验值)

2.2 径向分布函数

为了探究Ga91.6Sn8.4和10Li-Ga91.6Sn8.4的结构变化行为，主要选择对其径向分布函数做深入分析。图1为300 K下Ga91.6Sn8.4和10Li-Ga91.6Sn8.4的总径向分布函数图，total表征在距离中心原子处，找到另一个原子的相对概率。从图中可以看出，径向分布函数都有一个较高的主峰，表明体系都以短程有序为主。对于共晶Ga91.6Sn8.4，计算所得峰的位置和高度都与实验数据吻合较好，再一次验证本实验模型的准确性。相比于共晶Ga91.6Sn8.4，Li的引入使主峰位置由原来的0.283 nm移至0.280 nm，峰的高度也略微增大。另外，10Li-Ga91.6Sn8.4的第二峰有“劈裂”的趋势，为明显的非晶态特征，与团簇连接方式的层次性和不均匀性有关。团簇趋于密堆，表明10Li-Ga91.6Sn8.4体系有序度更高，暗示Li嵌入Ga91.6Sn8.4后Li-Ga-Sn体系会转变成固态。

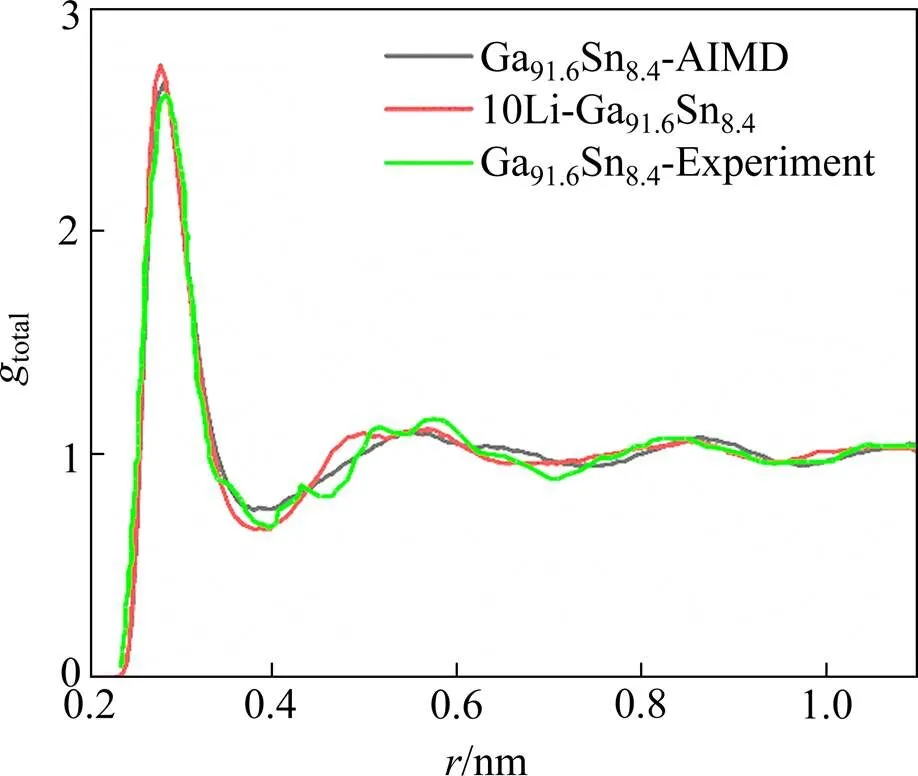
图1 Ga91.6Sn8.4和10Li-Ga91.6Sn8.4的总径向分布函数(绿色直线为实验数据[7])

为了更好地了解体系结构随Li引入的变化，进一步计算分态径向分布函数(亦称两体关联函数)αβ，它表征以α原子为中心，距离中心原子处找到β原子的相对大小。计算结果如图2所示，具体细节列于表3。可以看出，总径向分布函数中第一峰的位置主要取决于GaGa，这主要与Ga原子数较多有关。Ga91.6Sn8.4与10Li-Ga91.6Sn8.4相比，Li的加入对Ga-Sn二元合金的结构并没有很大的影响。对于共晶Ga91.6Sn8.4，第一峰的位置SnSn(0.318 nm)>GaSn(0.3 nm)>GaGa(0.277 nm)，这与原子半径的大小有关，Sn的原子半径大于Ga。同时还可以得出主峰SnSn的高度明显高于GaGa，GaSn最小，表明在该体系中，Ga与Sn之间的相互作用力较弱，Ga和Sn原子更倾向与同类原子聚集。对于无序结构10Li-Ga91.6Sn8.4，第一峰的位置LiSn(0.308 nm)>GaSn(0.302 nm)>LiGa(0.291 nm)。Li的原子半径比Sn的大，但是在这里，GaSn(0.302 nm)>LiGa(0.291 nm)，说明Li受到了较强的吸引作用，在所有异质原子对中，第一峰的高度LiSn明显高于LiGa，GaSn仍然最小，表明Li与Sn之间的亲和力较强。值得注意的是，LiLi表现为明显的中程有序，说明Li不同于Ga和Sn，Li原子不倾向于同类原子聚集。

除了定性分析以外，Δ指数可以用来定量表征异类原子之间的相互作用力[17]：

式中：为α与β原子之间相互作用力参数，%；rαβ，rββ，rαα分别表示gαβ中第一峰的位置，nm。根据式(2)，当Δr>0，表明异质原子倾向于分离，当Δr<0，表明异质原子倾向于结合。在共晶Ga91.6Sn8.4中，ΔrGaSn= 8.6%，说明Ga与Sn倾向于分离，该结论也曾在实验中得到证实[7]，共晶Ga91.6Sn8.4熔体中，Sn原子偏向于聚集，从而导致相分离。同理，在10Li-Ga91.6Sn8.4中，ΔrLiSn(−5.2%)<ΔrLiGa(−4.0%)<0<ΔrGaSn(6.7%)，说明Li原子同Sn和Ga原子相互吸引，同时Li与Sn原子之间的亲和力明显强于Li与Ga原子之间的亲和力，Ga与Sn仍表现为相互排斥。因此可预测，总径向分布函数中第二峰的“劈裂”可能与Li的引入使得体系倾向于形成Li-Sn和Li-Ga合金有关。当模拟时间无限延长，劈裂的峰逐渐分裂成两个峰，形成合金的径向分布函数。该预测可以从室温纯Ga液态金属电池放电现象得到证实[5]，随Li容量增加，体系逐渐固化，并且形成Li2Ga7以及LiGa合金。

(a)−(c) Radial distribution functions of Ga91.6Sn8.4and 10Li-Ga91.6Sn8.4; (d)−(f) Partial radial distribution functions of 10Li-Ga91.6Sn8.4

表3 Ga91.6Sn8.4和10Li-Ga91.6Sn8.4中径向分布函数第一峰位置

2.3 动力学性质

为了研究Ga91.6Sn8.4和10Li-Ga91.6Sn8.4中原子扩散系数的变化，进一步计算平衡构型下的均方位移(mean-square displacement, MSD)，结果如图3所示。各原子的均方位移与时间基本呈线性关系，Li的引入造成Ga和Sn的均方位移均减小，说明当Ga91.6Sn8.4嵌锂后Ga和Sn的扩散能力减弱，体系有“固化” 趋势。

结合均方位移，通过线性拟合得到扩散系数，同时由Stokes-Einstein关系[18]得出的黏度值列于表4。从表中看出，Sn原子的扩散系数比Ga原子小，这主要是由原子质量和原子间相互作用决定的。结果进一步表明Li原子的引入使得共晶Ga91.6Sn8.4二元合金中各原子扩散系数减小，其中Li原子的扩散系数最小，说明10Li-Ga91.6Sn8.4中，Li原子被紧紧束缚(在纯Li熔体中，Li的扩散系数应最大)，该结论与前述径向分布函数部分所得结论完全一致。与自扩散系数的变化规律相反，10Li-Ga91.6Sn8.4与Ga91.6Sn8.4相比，黏度显著增大，由原来与实验数据吻合较好的1.49 mPa·s增加到4.91 mPa·s。

图3 Ga91.6Sn8.4和10Li-Ga91.6Sn8.4中各原子的均方位移对比

表4 Ga91.6Sn8.4和10Li-Ga91.6Sn8.4中的原子扩散系数以及预测的黏度值(括号内为实验值)

3 结论

1) 采用第一性原理分子动力学方法，计算得到无序Ga91.6Sn8.4和10Li-Ga91.6Sn8.4的混合焓。300 K时Ga91.6Sn8.4的混合焓为正值，而10Li-Ga91.6Sn8.4的混合焓为负值，表明共晶Ga91.6Sn8.4嵌Li过程放出热量。

2) 在300 K下，Ga91.6Sn8.4和10Li-Ga91.6Sn8.4主要以短程有序为主，Ga91.6Sn8.4中Ga与Sn的相互作用较弱，倾向于同类原子聚集；10Li-Ga91.6Sn8.4中，Li的引入对Ga-Sn二元合金的结构影响不大，但会造成体系的有序度增加，宏观上表现为熔点升高。

3) 10Li-Ga91.6Sn8.4中，Li-Sn之间的亲和力明显强于Li-Ga，所以在嵌锂过程中，Li更倾向于先和Sn结合，再与Ga结合。

4) Ga91.6Sn8.4嵌锂后，各原子的扩散系数与Ga91.6Sn8.4相比略有减小，嵌锂过程有固化趋势，其中Li原子扩散系数最小，这主要与10Li-Ga91.6Sn8.4中异类原子之间的亲和力有关。

[1] KIM H, BOYSEN D A, NEWHOUSE J M, et al. Liquid metal batteries: past, present, and future[J]. Chemical Reviews, 2013, 113(3): 2075−2099.

[2] 张坤, 彭勃, 郭姣姣. 化学储能技术在大规模储能领域中的应用现状与前景分析[J]. 电力电容器与无功补偿, 2016, 37(2): 57−59.

ZHANG Kun, PENG Bo, GUO Jiaojiao. Application status and prospective analysis of chemical energy storage technology in large-scale energy storage field[J]. Power Capacitor & Reactive Power Compensation, 2016, 37(2): 57−59.

[3] EAKER C B, DICKEY M D. Liquid metal actuation by electrical control of interfacial tension[J]. Applied Physics Reviews, 2016, 3(3): 149−162.

[4] GUO X, ZHANG L, DING Y, et al. Room-temperature liquid metal and alloy systems for energy storage applications[J]. Energy & Environmental Science, 2019, 12(9): 2605−2619.

[5] DESHPANDE R D, LI J, CHENG Y, et al. Liquid metal alloys as self-healing negative electrodes for lithium ion batteries[J]. Journal of the Electrochemical Society, 2011, 158(8): 845− 849.

[6] WU Y, HUANG L, HUANG X, et al. A room-temperature liquid metal-based self-healing anode for lithium-ion batteries with an ultra-long cycle life[J]. Energy & Environ Science, 2017, 10(8): 1854−1861.

[7] ZHAO X, BAI Y, LI X, et al. The dissection of atomic clusters with local structure in Ga-Sn alloy melts[J]. AIP Advances, 2018, 8(10): 1−6.

[8] WOODWARD C, ASTA M, TRINKLE D R, et al. Ab initio simulations of molten Ni alloys[J]. Journal of Applied Physics, 2010, 107(11): 1861−1888.

[9] YU S, KAVIANY M. Electrical, thermal, and species transport properties of liquid eutectic Ga-In and Ga-In-Sn from first principles[J]. Journal of Physical Chemistry C, 2014, 140(6): 064303.

[10] HOSHINO K. Structure of liquid metals by ab initio molecular-dynamics simulations[J]. Journal of Physics Condensed Matter, 2009, 21(47): 474212.

[11] 刘媛媛, 贾国斌, 杨斌. 液态Pb-Cu合金结构与扩散性质的分子动力学模拟[J]. 材料导报, 2011, 25(6): 5−8.

LIU Yuanyuan, JIA Guobin, YANG Bin. Molecular dynamics simulation of the structure and diffusion properties of liquid Pb-Cu alloys[J]. Materials Reports, 2011, 25(6): 5−8.

[12] KRESSE G, FURTHMÜLLER J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set-sciencedirect[J]. Computational Materials Science, 1996, 6(1): 15−50.

[13] KRESSE G, FURTHMÜLLER J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J]. Physical Review B, 1996, 54(16): 11169−11186.

[14] NOSÉ S. A unified formulation of the constant temperature molecular dynamics methods[J]. Journal of Chemical Physics, 1984, 81(1): 511−519.

[15] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple[J]. Physical Review Letters, 1998, 77(18): 3865−3868.

[16] GANCARZ T. Density, surface tension and viscosity of Ga-Sn alloys[J]. Journal of Molecular Liquids, 2017, 241: 231−236.

[17] LI D, DELSANTE S, GONG W, et al. Partial and integral enthalpies of mixing of Ag-Ga-Sn liquid alloys[J]. Thermochim Acta, 2011, 523(1/2): 51−62.

[18] DOBOSZ A, PLEVACHUK Y, SKLYARCHUK V, et al. The influence of Li on the thermophysical properties of liquid Ga-Sn-Zn eutectic alloys[J]. Journal of Materials Science Materials in Electronics, 2019, 30(20): 18970−18980.

[19] FELS J, BERGER P, REICHMANN T L, et al. Calorimetric studies of mixing enthalpy in the liquid system Ga-Li, and Ga-Li-Sn[J]. Journal of Molecular Liquids, 2019, 295: 111578.

[20] 张强, 陈辉, 秦敬玉. Ga-Sn合金液态结构研究[J]. 金属功能材料, 2018, 25(4): 13−16.

ZHANG Qiang, CHEN Hui, QIN Jingyu. Study on liquid structure of Ga-Sn alloy[J]. Metal Functional Materials, 2018, 25(4): 13−16.

[21] FRENKEL J I. Kinetic Theory of Liquids[M]. USA: Dover Publications, 1955: 4820−4821.

Ab initio molecular dynamics study on eutectic Ga-Sn and 10Li-GaSn

DING An, WANG Jianchuan

(State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China)

The eutectic Ga91.6Sn8.4liquid metal can be served as the anode in Li-ion batteries. In this paper, the structure and kinetic properties of Ga91.6Sn8.4and Ga91.6Sn8.4with 10% (mole fraction, %, the same below) lithium intercalation (10Li-Ga91.6Sn8.4) were compared and analyzed by ab initio molecular dynamics. Calculation results show that there is no obvious differences in liquid structure between Ga91.6Sn8.4and 10Li-Ga91.6Sn8.4, both of them exhibit short-range order. The introduction of Li induces the second peak of the radial distribution function of 10Li-Ga91.6Sn8.4appear “split”, indicating that the order of the system increases and the melting points increases. In 10 Li-Ga91.6Sn8.4, the intercalation of Li reduces the diffusion coefficient of each atom in the system, and the attraction between Li-Sn atoms is significantly stronger than that of Li-Ga. Therefore, during the charging process, the Ga91.6Sn8.4Li-ion liquid metal battery exhibits the tendency of liquid-to-solid transition.

Li-Ga-Sn system; ab initio molecular dynamics; liquid structure; diffusion coefficient; viscosity

10.19976/j.cnki.43-1448/TF.2022014

O756

A

1673-0224(2022)04-345-06

中德合作研究小组资助项目(GZ1528)

2022−02−28；

2022−05−04

王建川，副教授，博士。电话：13080566873；E-mail: jcw7128@126.com

(编辑 陈洁)