褶皱对碳纤维复合材料层合板压缩性能的影响

叶 梯曾昭炜马铭泽

（1 中国民用航空飞行学院 航空工程学院，广汉 618307）

（2 机械结构力学及控制国家重点实验室，南京航空航天大学，南京 210016）

0 引言

复合材料使用范围越来越广、使用量越来越大，这给复合材料的生产制造带来了挑战。虽然复合材料制造工艺日益成熟，但仍不可避免地会产生部分缺陷工件。常见的制造缺陷包括分层、孔隙、杂质、纤维褶皱等［1-2］，准确评估初始缺陷对结构件的力学性能的影响程度具有重要的工程意义。

纤维褶皱是对结构承载能力影响较大的一种初始缺陷，国内外学者对其开展了大量的研究。S.Mukhopadhyay 等［3］通过试验和有限元分析的方法，研究了含纤维褶皱层合板的压缩失效机理，分析结果与试验结果吻合良好。论文指出在褶皱程度较低时，层合板的失效模式以纤维断裂为主，而在褶皱程度较高时，失效主要由分层和基体开裂引起。于晓东等［4］通过试验和有限元分析方法研究了褶皱对L型复合材料层合板性能的影响，试验表明分层损伤和基体开裂是L型层合板的主要失效模式，褶皱对整体刚度影响较小，但会显著降低承载能力，采用Hashin 准则的有限元分析结果与试验吻合良好。P.Davidson 等［5］通过试验和有限元方法研究了褶皱错位角度以及褶皱高度对碳纤维复合材料抗压强度的影响。结果表明二者均会明显降低材料抗压强度，最终破坏模式主要受高宽比影响，大的高宽比失效模式为纤维折曲（kink），高宽比较小时失效模式为滑移（slip）。V.Dattoma 等［6］通过试验方法研究了褶皱对复合材料开孔拉伸和开孔压缩性能的影响。结果显示褶皱的存在使得拉伸和压缩强度和刚度均明显下降，在破坏模式上，拉伸在载荷达到极限载荷的43%～59%间会出现分层损伤，而在压缩载荷下除了低刚度铺层试验件外，未见分层损伤。B. D. Allison等［7］对玻璃纤维复合材料褶皱试验件进行了三点弯曲试验，并提出了针对该类试验件的理论求解方法，理论解与试验结果相符，褶皱程度大的试验件抗弯强度降低37%。钱若力等［8］通过数值分析方法，研究了玻璃纤维褶皱对层合板拉伸性能的影响。论文认为褶皱高宽比的增大会使得玻璃纤维层合板失效载荷严重降低，层合板在拉伸过程中会发生弯曲变形，并最终在褶皱变形区域完全失效。Z.H.Ning 等［9］针对面外纤维褶皱提出了一种三维弹塑性损伤分析模型，模型将复合材料本构模型考虑为弹塑性模型，采用渐进损伤方法，并参考LaRC05 准则将复合材料的失效模式分为纤维拉伸失效、基体失效、纤维扭折以及分层失效等4 种模式。论文将该模型运用于已有的含纤维褶皱试验分析，得到了比参考文献弹性本构模型更为准确的分析结果。申川川［10］等认为单一褶皱缺陷的行为演化不能有效地控制批量构件性能的一致性，提出了一种考虑褶皱形态正交分布和空间位置随机分布的分散性模型，并将该模型与有限元方法结合运用在缺陷层合板的静载荷和冲击响应分析上，得到了相关力学性能的统计学指标。文献［11-12］设计了纤维重叠和纤维褶皱试验件并进行了疲劳试验，结果表明纤维重叠对层合板疲劳寿命影响较小，然而纤维褶皱能使疲劳寿命降低50%。文献［13］在应力比为0.1的拉-拉载荷下进行了褶皱复合材料疲劳试验，同时提出了一种可用于三维模型的疲劳强度有限元模型。结果指出，在高周疲劳载荷下，褶皱会使得疲劳寿命降低一个数量级左右，主要原因为褶皱会造成分层损伤过早出现。在面内损伤研究方面，文献［14-16］分别对含面内褶皱复合材料的拉伸强度、压缩强度、抗弯强度进行了研究，指出含面内褶皱试验件三种强度均会明显低于无褶皱试验件。

可以看到，学者们已通过试验和有限元分析等方法对纤维褶皱形态、褶皱对拉伸压缩弯曲等力学性能的影响、褶皱对疲劳性能的影响等方面进行了大量研究，并取得了较多成果。但褶皱的拓扑类型种类繁多，失效模式众多，不同复合材料类型和铺层类型性能对褶皱的敏感度也不尽相同，目前还难有通用的理论方法适用于所有的褶皱分析。

本文旨在对工程生产中遇到的一种纤维褶皱类型开展试验和有限元分析研究，以判断该类型褶皱对工件力学性能的影响程度。试验参考ASTM D6641—2014进行。有限元分析采用渐进损伤方法，以改进的Hashin 准则作为材料纤维失效、基体失效以及分层失效判据，采用连续介质损伤力学（CDM）方法，通过引入基于断裂能的损伤变量的方法表征材料初始失效发生后的性能退化规律，方法通过自编Umat子程序实现。

1 试验

1.1 试验件设计

根据生产中产生的褶皱几何形态，设计了适用于ASTM D6641—2014的试验件。试验件铺层为［45/0/-45/90］3S，总铺层数为24，单层厚度为0.19 mm。试验件整体尺寸为140 mm×12 mm×4.56 mm，在其纵向中心处设计有褶皱，如图1所示。褶皱段长6 mm，褶皱段试验件凸起（凹陷）高度水平方向按余弦函数曲线变化，铺层方向从上到下逐渐降低，最下层凸起（凹陷）高度为0。定义褶皱程度为h/t，t为正常厚度，h为凸起（凹陷）最大尺寸。设计了褶皱程度为凸起10%、凸起20%、凸起30%、凹陷10%、凹陷20%、凹陷30%以及正常试验件等7组试验件，每组试验件各6件。

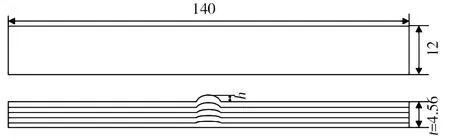
图1 褶皱试验件示意图Fig.1 Schematic diagram of wrinkle test piece

1.2 压缩性能测试

根据ASTM D6641—2014，采用标准压缩试验夹具进行试验。试验设备为济南试验机厂WDWE2000 电子万能试验机，精度0.5%。试验过程采用位移加载，首先进行预加载消除安装间隙，然后以恒速率加载至试验件破坏，加载速率1 mm/min。试验中载荷、位移等数据均由试验控制器采集。试验设备及夹具如图2所示，试验过程全程录像。

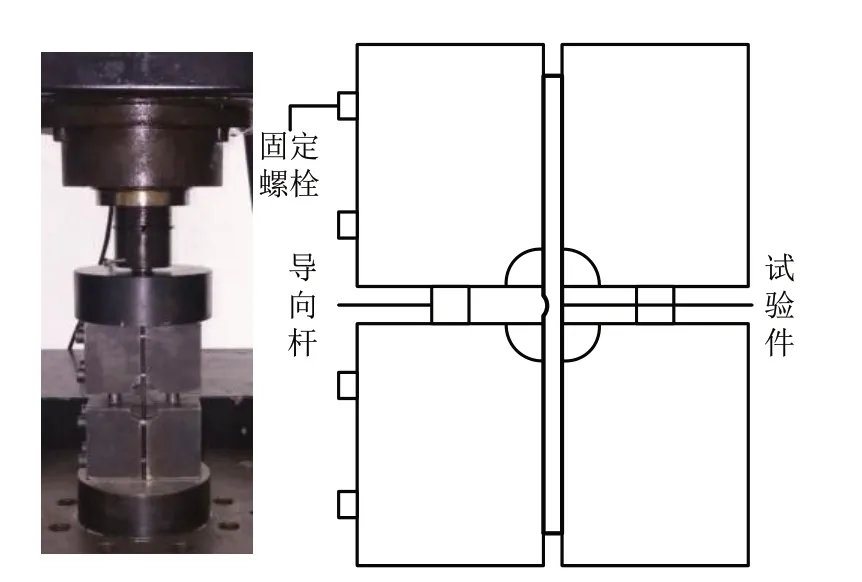
图2 试验设备及夹具Fig.2 Test equipment and fixture

2 有限元分析

为进一步研究试验件破坏机理，在试验的基础上进行了有限元分析研究。分析采用渐进损伤方法进行，渐进损伤理论认为材料的损伤不会使试件瞬间破坏，而是使材料的性能发生退化，随着载荷的不断增大，性能不断降低直至完全破坏。材料的损伤起始的判定（失效准则）以及性能退化的规律是渐进损伤分析的核心。

2.1 失效准则

Hashin失效准则［17］凭借其较好的预测精准度以及可以区分不同的失效模式等优点已被许多的学者用于预测复合材料失效，但其无法对分层失效进行有效预测。考虑到分层的存在，本文选取Olmedo改进的hashin准则作为损伤起始判据，该准则将损伤分为纤维损伤、基体损伤以及分层损伤，具体表达式为［18］：

纤维拉伸失效（ε11＞0）

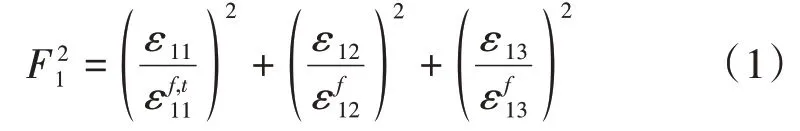
纤维压缩失效（ε11＜0）

基体拉伸失效（ε22+ε33≥0）

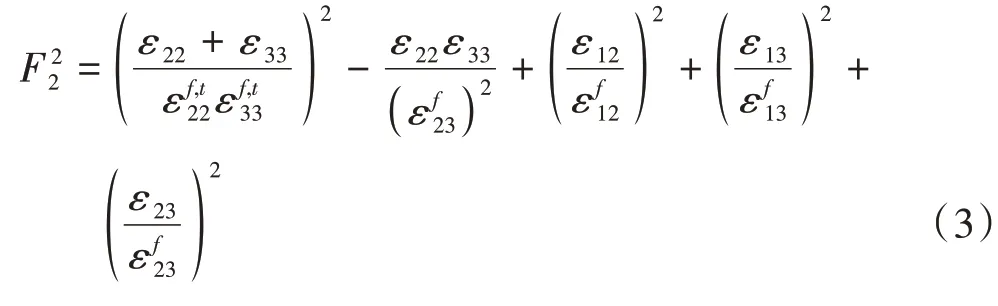
基体压缩失效（ε22+ε33＜0）

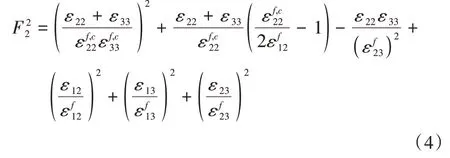
分层失效（ε33≥0）

2.2 性能退化准则

当材料出现损伤后，材料的承载能力下降，模型采用连续介质损伤力学（CDM）方法，通过引入损伤变量来表征材料性能退化。损伤后材料应力应变关系为

式中，Cd为损伤后的材料刚度矩阵，由损伤变量和初始刚度矩阵确定，由式（7）～式（9）计算可得。

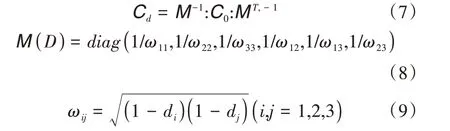
式中，di为损伤变量，1，2，3 分别表征纤维损伤、基体损伤以及分层损伤。di为0 是表示完全未损伤，di为1是表示完全破坏，材料从刚出现损伤到最终完全损伤，di从0逐渐增加到1，详细定义参考文献［19］中考虑断裂能的刚度退化准则。

拉伸失效

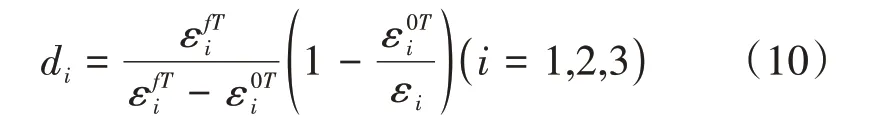
压缩失效

考虑到损伤演化是个不可逆的过程，材料一旦发生破坏其性能不能再恢复，因此计算模型中di均取损伤历史最大值。

2.3 分析流程

上述失效准则和性能退化准则均通过Abaqus用户子程序接口Umat 实现。Abaqus 主程序完成载荷步更新、平衡方程建立、平衡方程求解等内容；Umat子程序通过从主程序获取应变增量和上一步状态变量等信息，计算积分点应力应变状态并更新状态变量、进行性能退化并将数值返还主程序。状态变量用于表征材料损伤以及性能退化情况。整体有限元分析流程如图3所示。

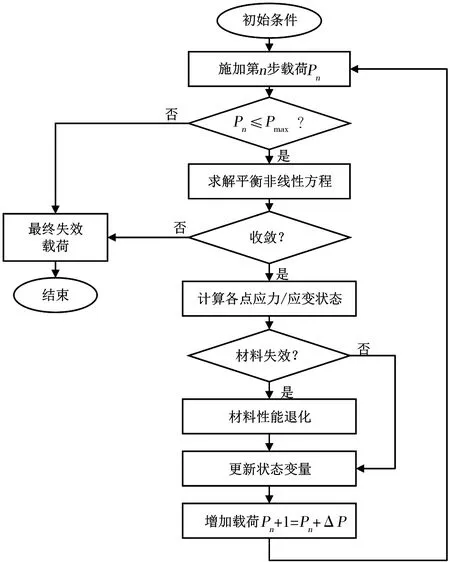
图3 有限元分析流程图Fig.3 Flow chart of finite element analysis

2.4 有限元建模

为减小计算量，有限元模型仅考虑试验段，忽略两端夹持段。所建立有限元模型如图4所示，单层板材料性能参数如表1所示。

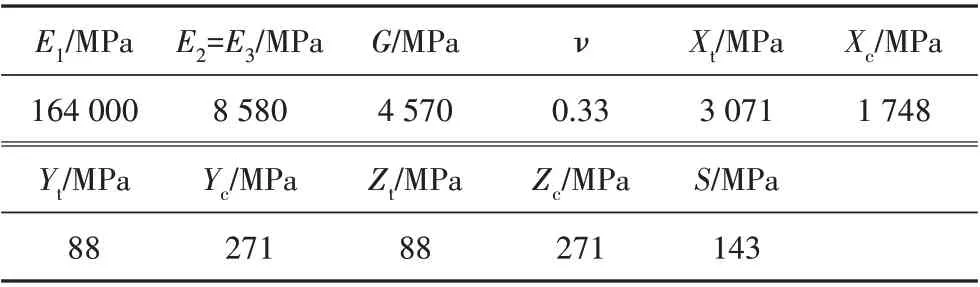
表1 材料属性Tab.1 Material properties

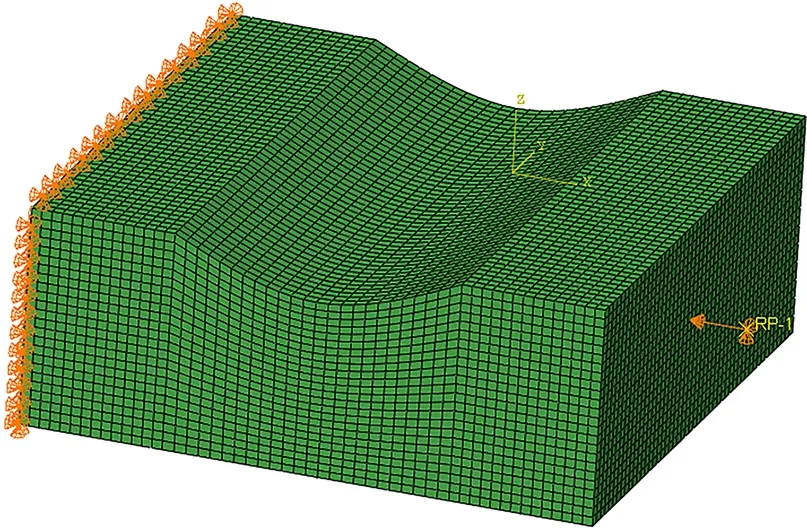
图4 有限元模型Fig.4 Finite element model

模型网格单元类型采用C3D8R，网格在厚度方向共24层，每层网格对应一层单层板，逐一赋予铺层方向。载荷及边界条件为一端固支，另一端采用位移加载。为方便读取载荷信息，建立了参考点并与加载断面耦合，位移载荷施加在参考点上。

3 结果分析

3.1 褶皱对压缩强度的影响

不同褶皱程度试验件载荷位移曲线趋势均相同，以凹陷20%试件为例进行分析，载荷位移曲线如图5所示（注：由于分析模型未考虑夹持段，图中对仿真曲线横坐标进行了比例放大）。

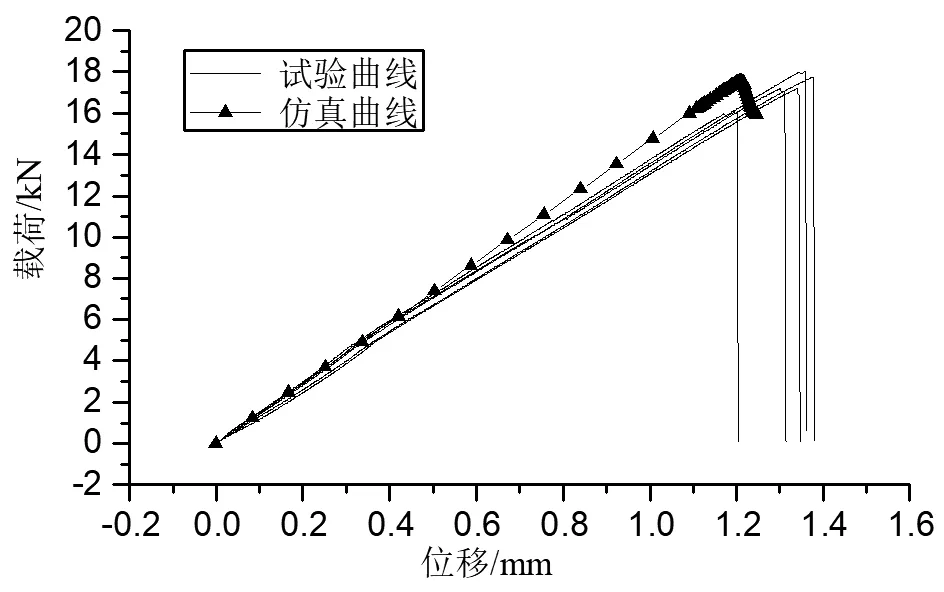
图5 凹陷20%试件载荷位移曲线Fig.5 Load displacement curves of 20%sunken test pieces

由图5可知，初始阶段载荷随位移呈线性增加趋势，在达到载荷峰值前很小一段载荷内出现斜率减小，表明此时已出现损伤；损伤使得周围材料受载加剧从而迅速破坏，因此很快出现载荷急剧下降，试验件完全破坏失去承载能力，此过程试验中伴有巨响，试验停止。极限载荷分析值与试验值符合良好，载荷位移曲线整体规律也与试验一致。不同褶皱程度极限破坏载荷与仿真结果如表2所示，可以看到试验离散系数均在10%以内，试验结果良好；仿真值与试验平均值误差也相对较小；数据表明褶皱对试验件承载能力影响较大，并且褶皱程度越大，试件承载能力越低，其中凹陷30%试件相比完好试件极限破坏载荷下降了58.48%。对比同等褶皱程度的凸起凹陷试验件可知，凹陷缺陷比凸起缺陷对试件承载能力影响更大。

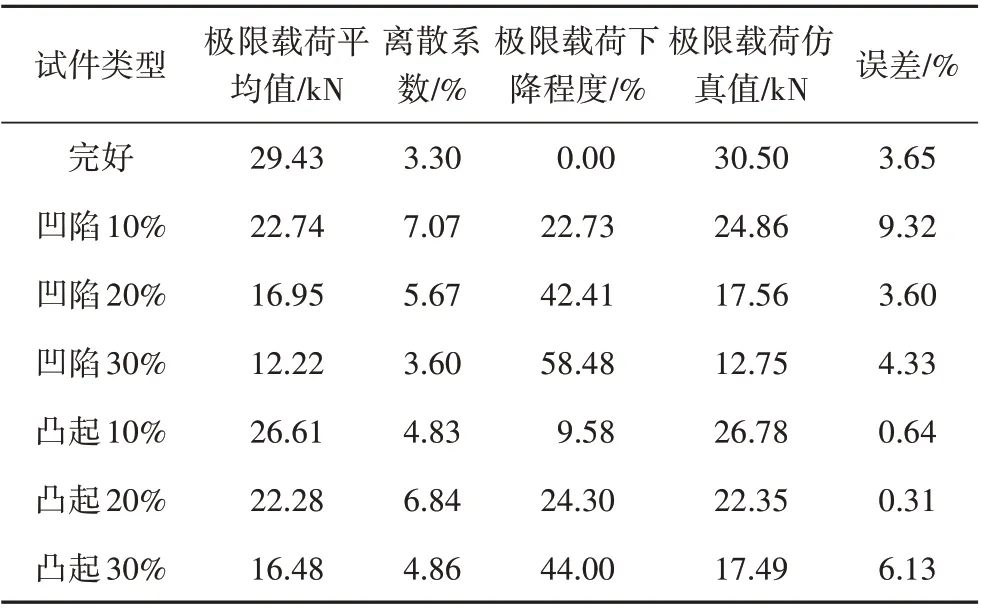
表2 试验破坏载荷与分析破坏载荷Tab.2 Test failure load and analytical failure load

3.2 褶皱对试件刚度的影响

为研究褶皱对试验件刚度的影响，图6对比了不同褶皱程度典型试验载荷位移曲线。对刚度的研究主要考虑载荷位移曲线的弹性段，由图可知，褶皱对试件刚度存在较大影响，其中褶皱30%试验件刚度（约10.46 kN/mm）相比完好试验件刚度（约16.30 kN/mm）降低35.80%；试验件刚度随褶皱程度增大呈下降趋势。

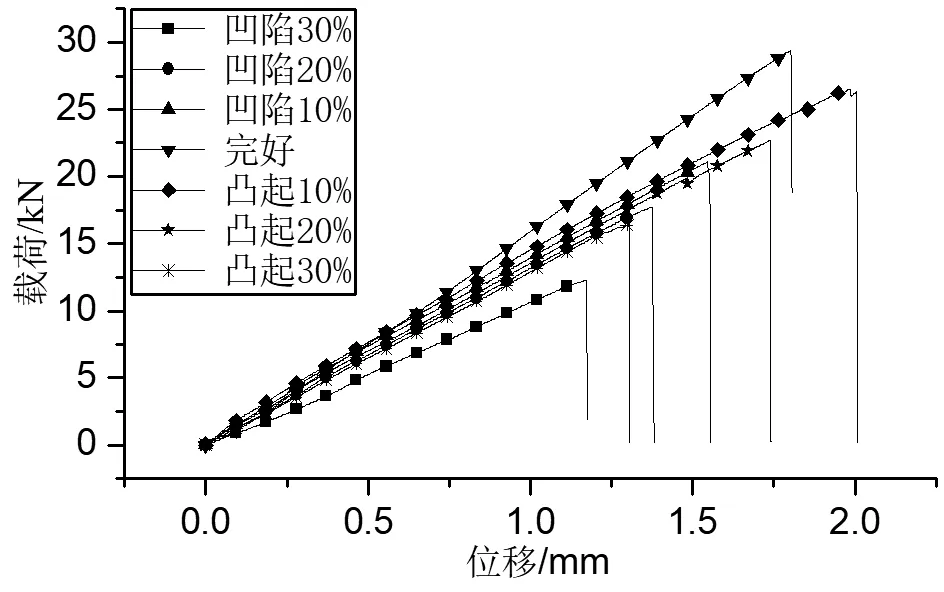
图6 不同褶皱程度试验件刚度对比图Fig.6 Stiffness comparison of test pieces with different wrinkle degrees

3.3 损伤扩展过程分析

不同褶皱程度试件的损伤的出现和发展规律基本相同，仅发生的时间有所差异。这里以凹陷20%试验件为例进行分析。试验中典型破坏模式如图7所示，破坏发生在褶皱处，最终的失效包括了基体损伤、分层损伤以及纤维断裂等多种损伤。从有限元分析过程来看，首先出现的是基体损伤，基体损伤后很快出现了分层损伤，最后出现纤维损伤。三种损伤中，基体损伤出现最早也最严重，图8 展示了试验件基体损伤起始以及扩展的过程。在位移达到0.92 mm 时，首先出现了基体失效，由于损伤仅仅出现在少量单元，损伤量也较小，载荷位移曲线刚度变化不明显；然后损伤开始扩展，单元损伤量和损伤单元数逐步增大，在位移达到1.21 mm 时，载荷位移曲线斜率已出现明显降低，载荷达到最大值；此后损伤继续扩大，载荷随位移增大而减小，试件很快完全破坏。图中损伤出现位置与试验件最终破坏位置吻合，验证了分析的可靠性。

图7 凹陷20%试件破坏情况Fig.7 Damage of 20%sunken test piece

图8 基体损伤演化Fig.8 Evolution of matrix damage

4 结论

（1）纤维褶皱会明显降低复合材料压缩强度，褶皱程度为30%的凹陷试验件比完好试验件极限破坏载荷降低了58.48%。

（2）同等褶皱程度情况下，凹陷褶皱比凸起褶皱对复合材料压缩强度影响更为严重。

（3）纤维褶皱对复合材料试件刚度也存在较大影响，褶皱程度为30%的凹陷试验件比完好试验件刚度下降35.80%。

（4）文中所采用有限元模型能较好地预测褶皱试验件压缩强度，并能有效地模拟损伤的起始及扩展过程。试验件的损伤产生在褶皱处，以基体损伤开始，而后出现了分层损伤以及纤维损伤，并最终扩展至试件完全破坏。