润滑油对涡旋鼓风机平衡铁动力学特性的影响及其优化
刘兴旺,韩向阳,刘晓明,杨 欢,刘世成
(1.兰州理工大学 石油化工学院,兰州 730050;2.压缩机技术国家重点实验室,合肥 230031)
0 引言
涡旋鼓风机中主轴带动动涡旋盘做偏心运动会产生离心惯性力,因此常设计两块平衡铁来将其平衡[1-5]。为了节省空间及让运行转速绕开临界转速[6],通常只能将大平衡铁安放在充满润滑油的背压腔中,小平衡铁则固定在轴上或者电动机转子上。而大平衡铁在背压腔中转动会产生阻力矩。其不但会使机器的功耗增大,而且会使温度升高导致润滑油黏性下降,造成轴承磨损加剧。
近年来,对涡旋压缩机平衡铁在背压腔中运动及其结构优化,国内外学者主要做了如下研究,张文祥等[7]对涡旋压缩机流体的阻力损失进行分析与计算,得出了动涡盘,十字环,平衡铁运动导致的流动阻力损失计算式。李超等[8]模拟了平衡铁在空气中旋转的过程,发现了压差阻力是平衡铁产生功率损耗的主要原因。NAGAOKA等[9-10]针对制冷涡旋压缩机小平衡铁对底部润滑油搅动导致油位不足的问题,提出一种新结构避免了其对底部润滑油的搅拌,提升了制冷系统性能。郑勋[11]对平衡铁位置及结构分别进行调整和优化,降低了机器振动,为提升涡旋压缩机性能提供了可靠的理论依据。刘兴旺等[12-13]通过研究电动汽车涡旋压缩机的背压腔系统,得出了不同入口压力工况下背压腔流场分布发生规律性变化。还模拟了变转速工况下平衡铁在背压腔内对润滑油搅动的过程,发现轴向平衡力和轴向气体力周期性变化,并提出了变相位协调叠加轴向力的优化设计方法,使轴向平衡力振幅减小。但其都未研究变转速工况下不同结构的平衡铁在润滑油中转动受到阻力矩的规律。
本文以课题组自行研发的涡旋鼓风机为研究对象,提出将变转速工况与平衡铁表面流场进行关联研究,探究了变转速工况下平衡铁受到阻力矩的规律及原因,并对平衡铁进行优化,以减小其所受阻力矩及边界层分离损失。
1 背压腔及平衡铁结构
本文以课题组自行研发的涡旋鼓风机中的平衡铁及其所在的背压腔为研究对象。背压腔是由支架体,主轴及动涡旋盘装配后形成的充满润滑油的腔体,如图1所示。

图1 某涡旋鼓风机内部三维结构Fig.1 3d diagram of internal structure of a scroll blower
与平衡铁相关联的主要构件包括:动涡旋盘,主轴承,支架体,十字滑环,驱动轴承。平衡铁安装在主轴上随主轴在背压腔中一起旋转,而润滑油经过油路入口进入,通过背压腔,从油路出口流出。平衡铁结构如图2所示。

图2 平衡铁结构Fig.2 Structural diagram of the counterweight
2 平衡铁阻力矩分析
平衡铁在充满润滑油的背压腔中旋转,其阻力矩包括两部分,一是平衡铁各表面受到摩擦阻力而产生的摩擦阻力矩,二是平衡铁前后端面压力不同而导致的压差阻力矩。
2.1 摩擦阻力矩分析
依据摩擦定律可知,平衡铁每个表面的摩擦阻力矩可按下列公式计算。
平衡铁上下表面受到的摩擦阻力矩:
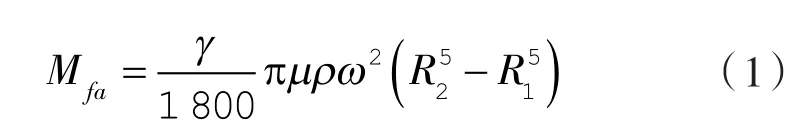
式中 γ——平衡铁前后端面之间夹角;
μ——摩擦系数;
ρ——介质密度;
ω——主轴旋转角速度;
R2——平衡铁外端半径;
R1——平衡铁内端半径。
平衡铁外表面受到的摩擦阻力矩Mfb:
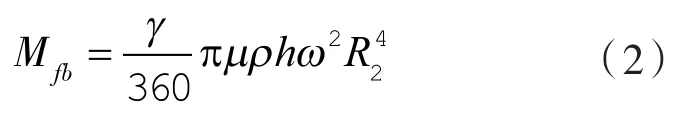
式中 h——平衡铁厚度。
平衡铁前后端面受到的摩擦阻力矩Mfc:
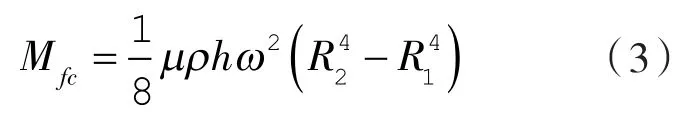
平衡铁所受到的总摩擦阻力矩Mf为:
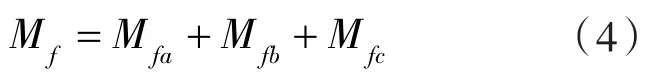
2.2 压差阻力矩
根据图3所示,平衡铁在背压腔中高速旋转时,前端面和后端面之间会形成一个压差,从而产生与运动方向相反的阻力矩。

图3 压差阻力矩Fig.3 Diagram of differential pressure resistance moment
Mh为平衡铁后端面由流体压力产生的与主轴转向相同的力矩,Mq为平衡铁前端面由流体压力产生的与主轴转向相反的力矩,故平衡铁运动中产生的总力矩Mp为两者之差。
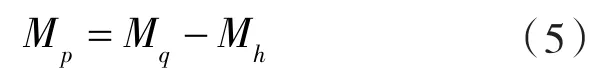
3 有限元分析
3.1 有限元模型简化及分析
本次研究选择FLUENT中的滑移网格模型(Sliding Mesh)来模拟不同转速下的平衡铁在充满润滑油的背压腔中转动的情况[14-15],并且根据平衡铁及背压腔实际情况,对模型做如下简化:
(1)略去平衡铁和轴相连接的部分,只留下实际可以提供离心惯性力的部分。
(2)忽略背压腔中的十字滑环、驱动轴承及动涡旋盘上去重孔对润滑油的影响。
以平衡铁及其所在的背压腔为研究对象,采用三维建模软件Solidworks建立出三维简化模型。如图4所示,模型主要构件包括一个圆柱形腔体、一个圆柱形出口管道,一个圆柱形入口管道、一块扇形平衡铁。其中平衡铁高度h=20 mm,平衡铁前后端面之间夹角γ=120,平衡铁外端半径R2=90 mm,背压腔内部半径r1=40 mm,外部半径r2=100 mm,背压腔总高度H=42mm,出入口管路直径d=10mm。并按照Fluent滑移网格的使用要求,将区域划分为动区域和静区域,动静区域之间的耦合则通过Interface面进行。
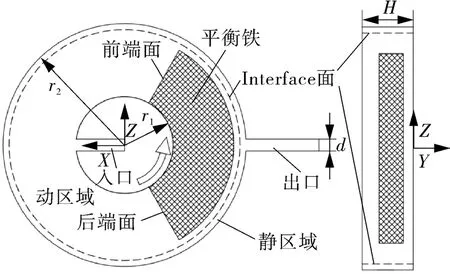
图4 背压腔简化模型Fig.4 Simplified model of back pressure chamber
3.2 网格划分
将计算模型划分为动、静区域,导入ICEM中选择六面体网格进行离散,并且对平衡铁周围网格进行局部加密,最后通过网格拼接技术将其耦合,采用滑移网格完成动,静区域之间的连接。图5示出划分好的六面体结构化网格模型,且为保证结果的可靠性,必须进行网格无关性验证。

图5 背压腔简化模型网格划分Fig.5 Meshing diagram of simplified model of back pressure chamber
对模型先后划分网格数为1 205 689,1 329 364和1 458 956个数量的网格,并且网格质量都达到0.6以上。入口压力为2.34 MPa,出口压力为2.24 MPa,并且设置转速为2 000 r/min。以研究关注的主轴转角θ=300°前后端面压力差作为观测量,对网格无关性进行验证,模拟结果见表1。

表1 不同网格划分模拟计算结果Tab.1 Simulation results of different meshing
由表1可发现,网格数量在增加到1 329 364时前后端面平均压力差变化较小,考虑在满足计算精度的情况下,为减少工作量及不浪费计算资源,故选择网格数为1 329 364进行计算模拟。
3.3 边界条件设置
运用FLUENT软件的滑移网格模型模拟不同转速工况下平衡铁在背压腔中旋转的过程。
计算条件设定如下:
(1)湍流计算模型采用RNG k-ε模型,近壁面采用标准壁面函数法。
(2)流场介质为赛润XGT416-150碳氢气体压缩机润滑油,该润滑油参数特性见表2。

表2 润滑油特性参数Tab.2 Characteristic parameter of lubricating oil
(3)转速分别选取 2 000,3 000,4 000,5 000,6 000 r/min进行模拟。
(4)背压腔入口压力为2.34 MPa,出口压力为2.24 MPa。
(5)在进行迭代计算时,通过添加4个监视窗口来分别监测出入口质量流量,以及平衡铁前后端面的平均压力。当出入口质量流量达到平衡及平衡铁前后端面平均压力达到周期性稳定时,便可以认为计算收敛。
3.4 平衡铁及背压腔流场分析
3.4.1 平衡铁压力场分析
虽然平衡铁前后端面的平均压力都随着主轴转过的角度发生周期性变化,但是其前后端面压力差却基本保持稳定,故选择一个角度观测其规律即可。
选取主轴转角300°,转速分别为2 000,4 000,6 000 r/min时的平衡铁压力场分布进行观测,平衡铁压力场分布如图6所示。
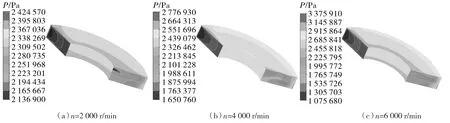
图6 不同转速平衡铁压力分布云图Fig.6 Pressure distribution nephogram of the counterweight at different rotational speeds
由图可见:(1)平衡铁壁面上的压力分布有沿着半径方向逐渐减小的趋势,最高压力在前端面外端,最小压力在后端面内端;(2)在主轴转速增加的条件下,出现了平衡铁壁面最高压力增大,最小压力减小的情况。这是由于平衡铁在背压腔中旋转时,前端部受流体压迫最为严重,且主轴转速一定时,线速度随着半径增大而增大,故外端受压最大,内端受压最小。当主轴转速升高,平衡铁前端面受迫强度加剧,外端压力升高;且流体绕流运动会在其后部形成尾迹,尾迹中存在的边界层分离也会加剧,从而消耗机械能,使压力降低,导致压力差加大。
图7示出2 000~6 000 r/min平衡铁前后两端面的平均压力与主轴转速关系曲线。结果显示,平衡铁前后端面的平均压力差随着转速增加而急剧增大。
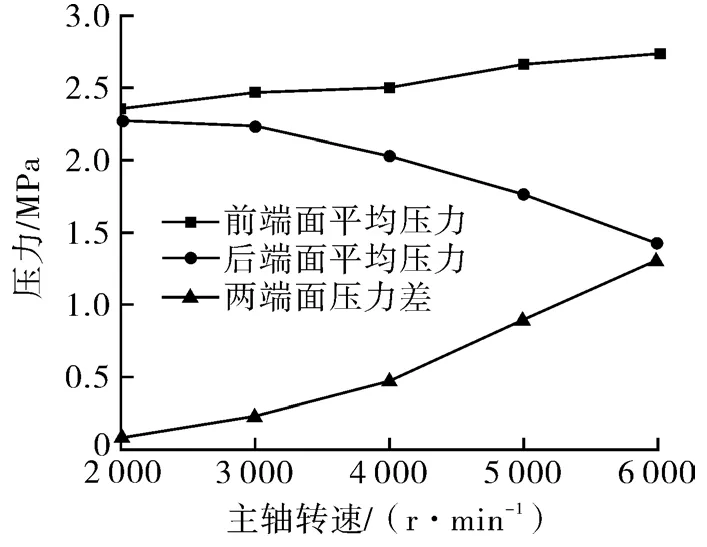
图7 前后端面平均压力与转速关系曲线Fig.7 Curve of relation between average pressure and rotational speed on front and rear faces
3.4.2 平衡铁周围速度场分析
建立背压腔径向辅助面,选取主轴转角为300°,转速2 000 r/min时平衡铁周围的速度分布场进行观测。图8示出径向辅助面速度流场,图9示出径向辅助面流场迹线。
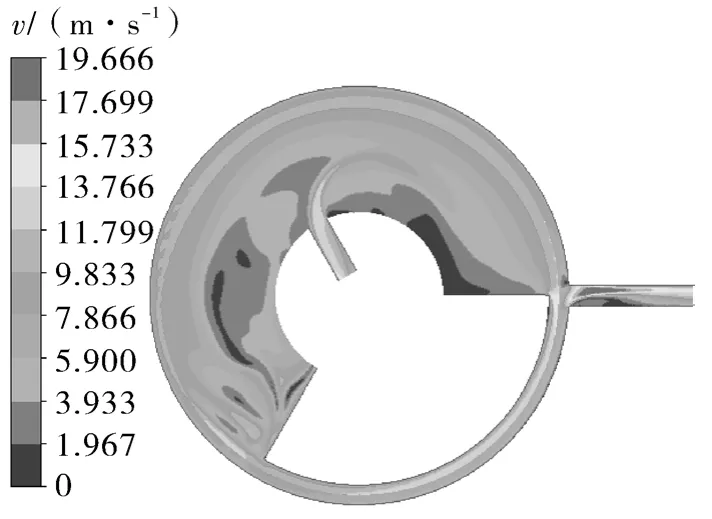
图8 辅助面速度流场Fig.8 Diagram of velocity flow field of auxiliary surface

图9 辅助面流场迹线Fig.9 Diagram of flow field trace of auxiliary surface
由图8,9可见,平衡铁后端面产生大量漩涡,说明流体流动到后端面时由于流通截面突变,产生了严重的边界层分离,致使尾迹区中压力降低,从而使平衡铁前后端面压力不相等,引起压差阻力。
3.4.3 平衡铁阻力矩计算
平衡铁所受摩擦阻力矩、压差阻力矩及总阻力矩随转速变化曲线如图10所示。

图10 各种阻力矩与转速关系曲线Fig.10 Curve of relation between various kinds of resistance moment and speed
由图10可见:(1)平衡铁所受摩擦阻力矩在主轴转速升高下呈小幅度增大趋势,而压差阻力矩则大幅增加;(2)在平衡铁所受到的两种阻力矩中,压差阻力矩最高占据了总阻力矩的83.9%,所以减少压差阻力矩是降低平衡铁所受总阻力矩的关键。
4 平衡铁结构优化设计
4.1 平衡铁结构优化
平衡铁前后端面与旋转方向垂直的结构导致产生了较大的压差阻力矩,故对模型进行机翼型优化。为保证平衡铁能提供足够离心惯性力,通过改变安装角度和平衡铁高度,使平衡铁重心和质量近似保持一致。如图11所示,其中最大的厚度h2=35 mm,前后端之间夹角γ1=120°。

图11 平衡铁优化模型Fig.11 Optimization model of the counterweight
针对优化后的模型,采用与上文相同的方法对其进行计算。
4.2 计算结果分析
4.2.1 优化后平衡铁压力场分析
选取主轴转角300°时,转速分别为2 000,4 000,6 000 r/min时平衡铁压力场分布进行观测。平衡铁的压力场分布如图12所示。由图可见:(1)平衡铁前端面的压力沿着半径逐渐降低,后端面的压力则是沿着圆周方向降低,这是由于机翼型平衡铁前端部受迫运动依然严重,但后端部绕流运动却更加均匀有序造成。(2)最高压力在前端面最外端,最低压力在前后端面交界处,这种情况降低了前端面平均压力,相对却提高了后端面平均压力,这就极大降低了前后端面压力差。这是由于机翼型平衡铁在流体流动时能更好贴合绕流物体表面,使发生分离位置更近尾部,导致尾迹区域变小,降低压力差。(3)主轴转速增加时,平衡铁壁面最高压力增大,最小压力减小。出现这种情况的原因和未优化前相似,随转速增大,平衡铁尾部尾迹区中边界层分离加剧,损耗了大量机械能,使前后端面压力差增大。(4)机翼型平衡铁有局部低压区域,最低压力在6 000 r/min时为611 798 Pa。由系统最低压强法可知,局部最低压力大于润滑油150 ℃下的饱和蒸汽压130 Pa,故该系统并不会产生空化现象,也不会发生空蚀[16-18]。

图12 优化后平衡铁压力分布云图Fig.12 Pressure distribution nephogram of the counterweight after optimization
图13示出优化后平衡铁前后两端面的平均压力与主轴转速关系曲线。

图13 优化后前后端面平均压力与转速关系曲线Fig.13 Curve of relation between average pressure and rotational speed on front and rear faces after optimization
结果显示,优化后平衡铁前后两端面压力差同样随着转速增加而快速增大。
比较图7,13可发现,在主轴转速相同时,优化后平衡铁前后端面压力差显著减小。这是因为机翼型平衡铁的流线型设计会使润滑油和平衡铁的分离位置后移,使尾迹区域变小,导致其前后端面压力差变小,最终降低平衡铁所受总阻力矩。
4.2.2 优化后平衡铁周围速度场分析
建立径向辅助面,选取主轴转角300°,转速2 000 r/min时平衡铁周围速度场进行观测。图14,15分别示出辅助面速度和迹线流场。

图14 优化后辅助面速度流场Fig.14 Diagram of velocity flow field of auxiliary surface after optimization
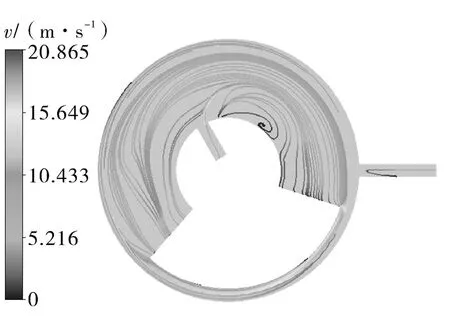
图15 优化后辅助面流场迹线Fig.15 The flow field trace diagram of auxiliary surface after optimization
由图14,15可知,平衡铁后端面局部漩涡基本消失,说明机翼型结构使平衡铁后端尾迹损失大为减小,降低了压差阻力。
4.2.3 优化后平衡铁阻力矩计算
图16示出优化后所受摩擦阻力矩,压差阻力矩,总阻力矩随转速变化关系曲线。

图16 优化后阻力矩与转速关系曲线Fig.16 Curve of relation between resistance moment and speed after optimization
比较图9,16可以看出,在相同转速下,优化后平衡铁所受摩擦阻力阻变化幅度较小。压差阻力矩最高占据了总阻力矩的71%。相比较优化前,其占据比例大幅度降低。
5 不同结构平衡铁对比分析
优化前后平衡铁在不同转速下所受总阻力矩如图17所示。对比可见,优化后平衡铁所受总阻力矩明显降低。
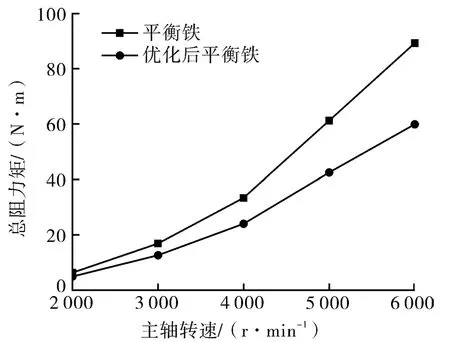
图17 两种平衡铁总阻力矩对比曲线Fig.17 Comparison curves of total resistance moments of two kinds of counterweight
从图18可以看出,优化后平衡铁所受总阻力矩降低的幅度由2 000 r/min时的21.9%,3 000 r/min时的 25.2%,4 000 r/min时的 28.1%,5 000 r/min时的30.6%,一直到6 000 r/min时的32.9%,优化效果随着转速的增加而变得更加明显。

图18 总阻力矩优化幅度曲线Fig.18 Optimized amplitude curve of the total resistance moment
由此发现,通过优化可以显著降低平衡铁在涡旋鼓风机内部运转受到的总阻力矩。
6 结论
(1)平衡铁表面压力场分布不均匀,最大压力出现在前端面外端,最小压力则出现在后端面内端。且主轴转速升高时,平衡铁前后端面平均压力差急剧增大。
(2)平衡铁所受压差阻力矩最高占据了总阻力矩的83.9%。且随着主轴转速升高,平衡铁受到的摩擦阻力矩缓慢增加,压差阻力矩则急剧增加。
(3)机翼型平衡铁使径向辅助面上的流线分布更加有序,边界层分离基本消失。且大幅度降低了其所受到的压差阻力矩,使得总阻力矩最高可降低32.9%。

