弹簧刚度对往复泵排液阀阀芯运动特性的影响

张扬恒，邢改兰，沈叶辉，陈德泉，周邵萍

（1.华东理工大学 承压系统与安全教育部重点实验室，上海 200237；2.上海福思特流体机械有限公司，上海 201709）

0 引言

往复泵作为一种容积式泵，具有高效率、额定压力高、流量大且可调节等优点，是石油化工等领域中重要的介质输送设备，由于泵阀为自动阀，阀芯在自身重力、弹簧力及液动力三者合力下运动，阀门开启时阀芯升程的控制及关闭时存在的滞后问题很大程度上影响着往复泵的容积效率和整个系统的工作效率［1-4］。随着计算流体动力学的发展，通过对往复泵工作过程进行数值模拟可以较为准确地反应真实流场分布和泵阀阀芯的运动规律，以往有学者研究阀门在固定开度下泵阀内流场的分布规律。张良等［5］研究了单柱塞泵在不同阀口开度和入口速度下工作腔内气穴流场的分布规律。郑淑娟等［6］通过给定液压锥阀阀芯运动的速度研究了阀芯在启闭过程受到瞬态液动力与阀开口度之间的关系。近年来逐渐有学者使用动网格技术来研究泵阀在恒定流量下阀芯的运动规律，指出泵阀运动性能受到弹簧刚度的影响显著，常玉连等［7］研究了对单向阀开启过程的影响，研究发现弹簧劲度系数与阀芯平衡位置位移呈线型递减关系。钱锦远等［8］对垂直管线型先导式截止阀在不同弹簧刚度下阀芯的冲击速度、稳定位移及瞬态位移进行了分析。以上研究针对传统的定刚度弹簧，随着先进制造技术的发展，生产结构复杂的变刚度弹簧变得越来越方便。目前变刚度弹簧广泛应用在汽车及其他减震缓冲装置中，但是在阀门领域的研究和应用较少，特别是在往复泵排液过程中，弹簧刚度对阀芯瞬态运动特性的影响机理研究不够深入。

本文通过对往复泵泵阀排液过程进行动态数值模拟，在此基础上，结合阀门弹簧刚度的设计准则，对比分析阀在定刚度弹簧、不同变刚度弹簧下对排液过程阀芯运动特性的影响为往复泵泵阀弹簧的优化设计提供一定的参考。

1 计算区域

1.1 研究对象

以某型号三联高压油往复泵为研究对象，其主要性能和结构参数：设计流量Q=16.06 m3/h，额定压力P=22 MPa，曲柄转速n=153 r/min，柱塞直径D=108 mm，冲程L=200 mm，曲柄半径R=100 mm，连杆长度r=540 mm，设计弹簧刚度K=5 022 N/m，阀芯质量m=1.3 kg。工作介质为导热油，密度ρ =817 kg/m3，黏度μ =0.000 28 N·s/m2。往复泵结构示意如图1所示。

图1 往复泵结构示意Fig.1 Structural diagram of reciprocating pump

1.2 流域抽取

本次研究围绕往复泵排液过程开展，柱塞工作面和阀芯运动方向如图2所示，为简化计算区域、提高计算效率，假设排液过程进液阀完全关闭，为提高计算效率，忽略进液阀区域、弹簧和阀芯导向筋等结构对流场的影响。

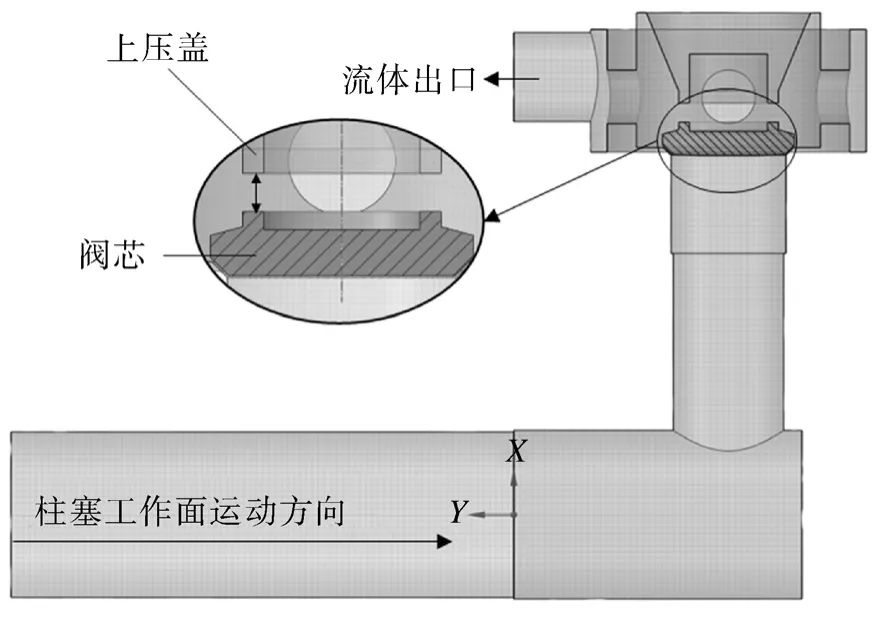
图2 流场结构示意Fig.2 Schematic diagram of flow field structure

1.3 网格划分

阀芯运动区域流道结构较为复杂，对该计算区域使用非结构网格进行离散，并且对阀芯附近区域进行局部网格加密。由于动网格技术的实现要求最小间隙处需要保留至少一层网格以使得流域保持连通的拓扑结构，因此使阀芯初始位置较完全闭合状态下上升1 mm，阀隙保留两层网格以提高计算的准确性和收敛性。柱塞壁面运动的区域流道结构规则，采用结构网格进行离散。对流场模型进行划分网格如图3所示。

图3 流场网格模型Fig.3 Flow field grid model

2 数值模拟

2.1 定义运动函数

（1）往复泵泵阀的阀芯在自身重力、弹簧力及流体作用在表面产生的压力差三者的合力共同作用下运动，根据牛顿第二定律结合阀芯受力分析可得其运动方程为：

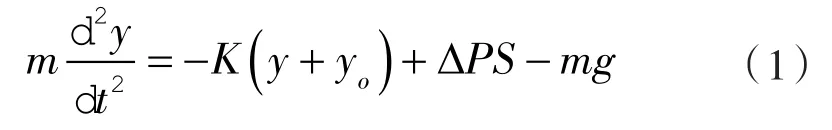
式中 m——阀芯质量，kg；

y——阀芯运动位移，m；

K——弹簧刚度系数，N/m；

yo——弹簧预压紧长度，m；

ΔP——阀芯表面压力差，Pa；

S——阀芯横截面面积，m2。

阀芯运动的数学模型通过UDF程序来建立，模型建立采用微分的思想，将运动时间平均分为若干个时间微元，首先在每个时间微元内对阀芯当前受力进行求解进行并将计算得到的加速度叠加到当前速度，然后每个时间步内的运动近似处理看作匀速运动，使用当前速度计算阀芯位移并进行叠加得到当前时间的阀芯位置。由于泵阀上压盖起到限位器的作用，需要对阀芯位移上限进行一定的限制。阀芯加速度、速度及位移迭代方程为：

式中 dt——单位时间步长，s；

a——阀芯加速度，m/s2；

n——下标，第n个时间步；

v——阀芯运动速度，m/s。

（2）柱塞工作面运动速度由动力端曲柄连杆机构和曲柄转速所决定，其速度方程为：

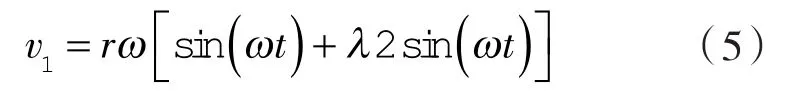
式中 v1——柱塞运动速度，m/s；

r——动力端曲柄半径，m；

ω——曲柄旋转速度，rad/s；

λ——曲柄半径与曲柄连杆长度的比值。

2.2 边界条件与求解设置

本文计算基于FLUENT求解器，湍流模型采用RNG k-epsilon模型。离散方程的求解算法采用适用瞬态问题的PISO算法，保证精度的同时具有较高收敛性的和求解效率。对流项采用二阶迎风格式，扩散项采用中心差分格式，减小松弛因子提高计算收敛性。通过In-Cylinder模型指定柱塞工作面的运动函数。通过编译加载UDF程序来指定阀芯的运动方程。由于仅研究往复泵排液过程，无进口边界条件，出口边界条件设置为压力出口，出口压力为22 MPa。

2.3 网格无关性验证

本文考察不同网格数量对阀芯运动所达到最大升程hmax的影响，进行网格无关性验证。结果如图4所示，当网格数量达到120万左右时阀芯最大升程基本不变，为保持计算精度和节省计算资源，最终网格单元数量维持在123.2万。

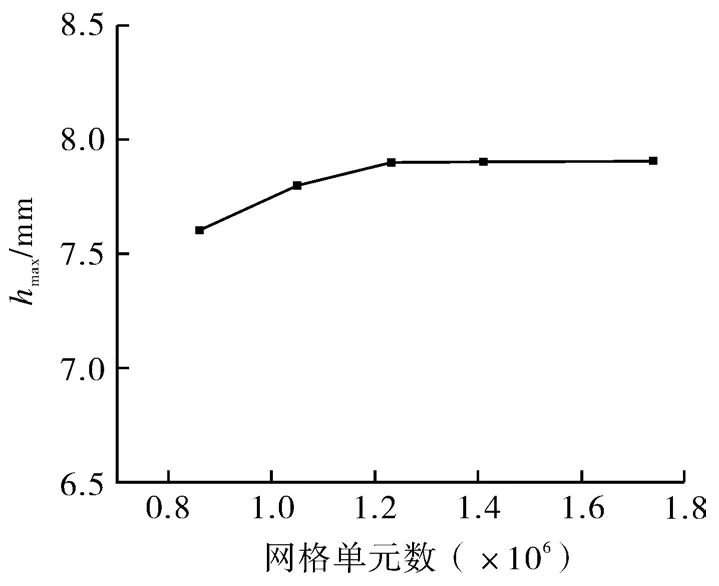
图4 网格无关性验证Fig.4 Grid independence verification

2.4 模型验证

为验证仿真结果的准确性，在三联往复泵原型泵上进行性能试验，在转速n=153 r/min，排出压力为0.45 MPa进行试验，导热油作为工作介质，使用流量计显示和监控流量大小，往复泵存在流量脉动特性，试验对流量的最大值进行记录，出口瞬时最大流量为50.14 m3/h，在该工况下仿真结果得到出口最大流量为53.6 m3/h，误差约为6.9%。考虑到试验下存在密封泄漏及测量误差等情况，该误差在允许接受的范围内。

3 结果分析

3.1 阀芯运动与泵阀内流场的动态耦合分析

图5示出在弹簧刚度系数K=5 022 N/m下通过仿真计算得出的阀芯升程与受力情况随时间变化的曲线，可以看出，阀芯受到的弹簧力随阀芯升程变化先增大后减小，液动力在阀芯开启阶段较大随后降低并且出现一定的波动，然后液动力呈现近似先增大后减小的规律，合力曲线表明阀芯在开启和关闭阶段均存在多次加速和减速过程。从升程曲线可以看出，阀芯的运动规律近似呈不规则的抛物线，运动在达到最大升程约为7.9 mm位置后开始回落并且在排液阶段最后时刻并未完全闭合，存在一定的关闭滞后高度。图6示出泵阀内流场剖面上的速度场云图，可以看出，随着时间的推移，在柱塞工作面对流体的推动作用下阀门内部整体流体流速先增大后减小，阀芯的运动使得阀门开度发生变化，并且流体流经阀隙时过流面积变化较大而导致速度变化梯度也较大，会产生较大的水力损失。

图5 阀芯升程与受到的弹簧力、液动力及合力随时间变化曲线Fig.5 The change curve of spool lift, spring force，fluid power and the resultant force with time

图6 不同时刻内流场剖面速度云图Fig.6 Velocity nephogram of the flow field profile at different times

3.2 定刚度弹簧对阀芯运动特性的影响

阀门弹簧的初始刚度K=5 022 N/mm，为研究弹簧刚度大小对阀芯运动和流场分布的影响规律，分别取弹簧刚度 K 为 2 511，4 017，6 026，7 533 N/mm进行分析。由图7和表1可以看出，随着弹簧刚度增大，阀芯的关闭滞后高度会减小，有利于提高往复泵的容积效率；但是弹簧刚度系数越大阀芯的升程越小，其主要原因是随着弹簧刚度的增大，相同位移处受到的弹簧阻力增大，导致升程随之降低，相同时刻阀隙过流面积减小导致水力损失增大，排液性能降低；并且由表1可以看出，排液过程随着弹簧刚度的增大柱塞工作面受到平均压力增大，根据受力情况，柱塞受动力端作用力和工作面流体压力，当柱塞工作面受到的平均压力增大时，工况不变的情况下动力端需要提供更大的作用力，导致整个系统的效率降低。

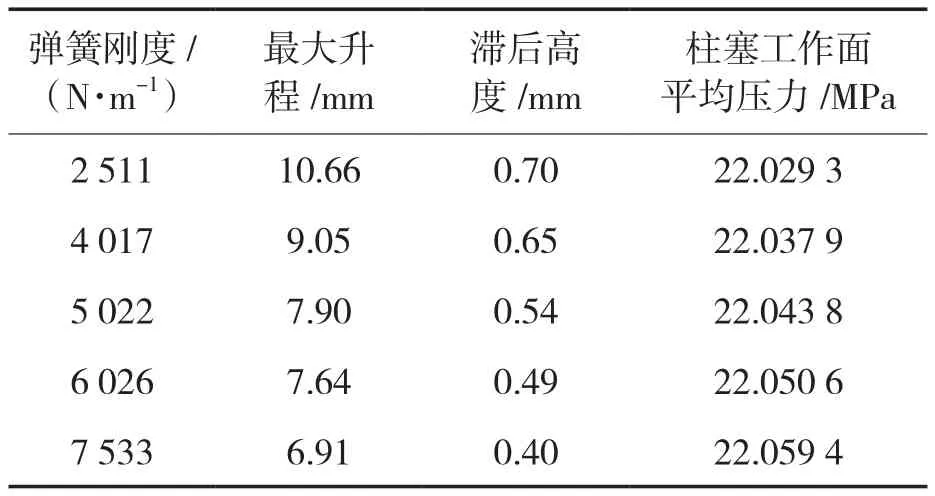
表1 不同定弹簧刚度仿真计算结果Tab.1 Simulation results of different constant spring stiffness

图7 不同弹簧刚度下阀芯升程随时间的变化曲线Fig.7 Variation curve of spool lift with time under different spring stiffness

3.3 变刚度弹簧对阀芯运动特性的影响

由于增大弹簧刚度会使水力损失增大导致泵效率降低，而减小弹簧刚度会使泵滞后高度增加，导致容积效率降低，针对上述问题，参考变刚度弹簧的设计思路，一般圆柱形螺旋弹簧的变形x计算公式［22］为：

式中 F——弹簧载荷，N；

D——弹簧中径，mm；

n——有效圈数；

G——弹簧材料的切变模量，GPa；

IP——弹簧材料截面极惯性矩，mm4。

将一般圆形截面材料的极惯性矩IP=πd4/32代入式（6）得刚度系数为：

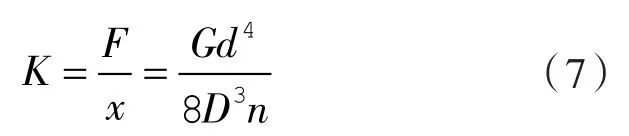
式中 d——簧丝横截面直径，mm。

因此，变刚度弹簧目前制造技术为通过改变弹簧的中径、弹簧的簧丝直径等方式来得到弹簧刚度系数为线性或非线性的螺旋弹簧，本文使弹簧的刚度系数与阀芯升程的关系为一次函数关系，即：

式中，a和b为常数，其取值的原则为：通过a和b控制刚度系数函数形式及变化的范围，当a＜0，刚度系数的取值呈减函数形式，阀芯位置在最低处时刚度最大，随阀芯位置升高刚度系数减小，在最高处刚度最小；当a＞0，刚度系数的取值呈增函数形式，阀芯位置在最低处时刚度最小，随阀芯位置升高刚度系数增大，在最高处刚度最大。变刚度系数Ⅰ和Ⅱ的刚度系数变化范围在500～1 500之间，其中变刚度系数Ⅰ为减函数形式，变刚度系数Ⅱ为增函数形式。变刚度系数Ⅲ和变刚度系数Ⅳ的刚度系数变化范围在800～1 200之间，其中变刚度系数Ⅲ为减函数形式，变刚度系数Ⅳ为增函数形式，具体参数见表2。

表2 不同弹簧类型函数参数取值Tab.2 Function parameter values of different spring types

分别对4种不同函数形式的变刚度弹簧进性仿真，计算结果分别如图8，9和表3所示。由图8可以看出,2组减函数形式的变刚度弹簧约在前0.03 s时间内，由于刚度系数较大，阀芯受到弹簧阻力较大运动速度较小。随着阀芯的上升约在0.03～0.1 s时间内，由于刚度系数减小，阀芯受到弹簧阻力减小运动速度高于其他3组弹簧，这使得其阀芯升程得到明显提高。约在0.1～0.2 s时间内，随着柱塞工作面运动速度减小，阀芯受到液动力减小并开始回落，回落阶段阀芯回落速度要高于其他3组弹簧，使得阀芯滞后高度更低，由于阀芯回落速度增大，受到的流体阻力增大使得在排液最后时刻阀芯回落速度减小，通过对比分析计算结果可以得出以下结论：

表3 不同变弹簧刚度类型仿真计算结果Tab.3 Simulation results of different variable spring stiffness types

图8 不同弹簧刚度类型下阀芯速度随时间的变化曲线Fig.8 Variation curve of spool speed with time under different spring stiffness types

图9 不同弹簧刚度类型下阀芯升程随时间的变化曲线Fig.9 Variation curve of spool lift with time under different spring stiffness types

（1）减函数形式的变刚度弹簧使阀芯的升程明显提高，且滞后高度明显降低，而柱塞工作面平均压力并影响不明显，其中变刚度系数Ⅰ使阀芯升程提高26.1%，滞后高度降低25.9%。变刚度系数Ⅲ使阀芯升程提高11.4%，滞后高度降低11.1%；增函数形式的变刚度弹簧对阀芯升程的影响并不明显，滞后高度明显升高，柱塞工作面平均压力影响不明显，其中变刚度系数Ⅱ使阀芯升程降低2.4%，滞后高度升高63%。变刚度系数Ⅳ使阀芯升程提高0.1%，滞后高度升高20.4%。

（2）弹簧的刚度系数变化范围取决于a和b的取值，减函数形式下的变刚度弹簧有利于提高往复泵泵阀的动力性能，使用减函数形式下的变刚度弹簧时，刚度系数变化范围增大，有利于提高阀芯升程和降低滞后高度。

4 结论

以某三联往复泵为研究对象，采用FLUENT软件对其泵阀排液过程进行动态数值模拟，在试验验证的基础上，分析了弹簧刚度对泵阀运动特性的影响，结论如下：

（1）定刚度系数弹簧下，随着刚度系数增大，阀芯的关闭滞后高度会减小，有利于提高往复泵的容积效率。但是刚度系数增大会使得阀芯的升程减小，相同时刻阀隙过流面积减小导致水力损失增大，排液性能降低，并且弹簧刚度的增大会使柱塞工作面受到平均压力增大，导致整个系统的效率降低。

（2）变刚度系数弹簧下，减函数形式的两组变刚度弹簧使阀芯的升程分别提高26.1%和11.4%，滞后高度分别降低25.9%和11.1%，而柱塞工作面平均压力并影响不明显；增函数形式的两组变刚度弹簧对阀芯升程分别降低2.4%和提高0.1%，滞后高度分别升高63%和20.4%，柱塞工作面平均压力影响不明显。

（3）减函数形式下的变刚度弹簧有利于提高阀芯升程和降低滞后高度。并且随着刚度系数变化范围增大，越有利于提高往复泵泵阀的运动性能。设计弹簧时可以在保证弹簧的强度要求及避免阀芯上升过程中与限位器的碰撞前提下，增大刚度系数变化范围。