接触式密封结构泄漏模型研究现状及发展

闫国华 ，武 松 ，刘 勇 ，刘中华

（1.中国民航大学 航空工程学院，天津 300300；2.中国民航大学 工程技术训练中心，天津 300300；3.中国航发沈阳发动机研究所，沈阳 110015）

0 引言

泄漏故障普遍存在于工业领域，因此，人们对密封泄漏问题的相关研究从未停止，并试图通过揭示其机理，采取应对措施。密封泄漏问题的研究主要包括密封表面接触和密封介质输运特性两部分内容［1］，文章将从这两方面进行评述。针对密封结构密封性能的研究侧重于从宏观力学和工艺参数等角度开展，以密封界面的接触面宽和接触压力作为密封性能的评价指标，缺少从微观尺度上揭示密封界面泄漏机理的研究工作。由于现有的加工技术不可能实现工程表面的绝对光滑，特别是在微观尺度对其进行观察可以发现接触表面是由许多大小不一的粗糙峰（微凸体）构成的［2-3］，所以当2个密封表面进行接触时，实际接触面积远小于理论接触面积，只有尺寸较大或较高的微凸体发生了实际接触，而其余未接触部分的空隙相互贯通，形成了泄漏通道，使流体介质在流动力的作用下从高压一侧流向低压一侧，进而造成泄漏故障的发生，如图1所示。因此密封界面微观接触问题的研究是密封界面泄漏机理研究的基础，也是接触式密封结构设计的重点和难点。本文首先扼要介绍了接触力学的发展历程，然后回顾了近年来在接触式密封结构泄漏模型研究中常用的方法，最后总结了未来可能成为该领域研究热点的一些思路和研究方法，为研究接触式密封结构的泄漏机理和密封结构的设计提供参考。

图1 粗糙表面接触示意Fig.1 Schematic diagram of rough surface contact

1 粗糙表面接触问题研究进展

1.1 Hertz接触力学模型

对于接触问题的研究最早可追溯至1781年法国物理学家查尔斯·库仑所提出的库伦摩擦定理，之后，德国物理学家HERTZ［4］在发表的文章中首次提出关于弹性接触的理论模型，至此，拉开了研究接触力学的序幕［1］。Hertz接触理论是其它经典接触模型的基础［5］，对进一步研究接触问题具有重要的理论研究价值［6-7］。但Hertz接触模型只适用于光滑且无摩擦的纯弹性变形，实际工程表面并不符合Hertz理论的应用条件，当接触应力超过弹性极限后，发生接触的微凸体将会发生弹塑性或完全塑性变形。

1.2 统计学接触模型

由于Hertz接触力学理论应用范围有限，所以对接触问题研究方法的改进和创新从未停止。其中GREENWOOD等［8］于1966年在Hertz接触理论基础上，结合统计学方法建立了一种粗糙表面法向接触模型，即经典的GW接触模型。该模型将两粗糙表面的接触简化为刚性光滑表面和粗糙表面的接触，如图2所示。

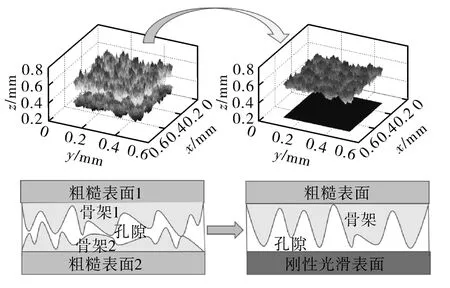
图2 粗糙表面接触简化模型Fig.2 Simplified contact model of rough surface

GW模型作为统计学模型的代表，此后半个多世纪，不断有学者对GW模型进行修正和改进［3］。GREENWOOD 等［9-10］在 GW 接触模型的基础上，相继推导出了球形粗糙表面之间和两粗糙平面之间的接触模型。CHANG等［11］利用微凸体塑性变形时体积不变原理将GW模型适用范围扩展至塑性变形阶段，形成了弹塑性接触模型（CEB模型）。ZHAO等［12］在CEB模型的基础上，考虑了弹性和塑性变形之间的弹塑性过渡阶段，建立了ZMC模型。之后又有学者［13］将弹塑性接触变形阶段进行细分得到前弹塑性变形、中弹塑性变形和后弹塑性变形，建立了连续临界点处粗糙度的弹塑性接触模型。ZHAO等［14］建立了考虑微凸体相互作用的统计学接触模型。上述这些模型在不同方面对GW模型进行了改进，使模型精度不断提高。但是文献［15］表明，这些表征模型的统计学参数都会不可避免的受到测量仪器分辨率和采样长度的影响，在不同观察尺度下会出现不同的结果。这种利用统计学参数来表征粗糙表面接触情况的模型其预测结果并非唯一、确定的，即具有尺度相关性。

1.3 分形接触模型

分形理论的出现很好地解决了模型存在的尺度相关问题［16］。利用尺度无关的分形参数替代尺度相关的统计学参数来表征粗糙表面。粗糙表面的分形特征与观察尺度无关，可以提供存在于分形表面上所有尺度范围内的全部表面形貌信息［15］。在不同的观测尺度下粗糙表面具有自相似特性，如图3所示。

图3 粗糙表面分形特性Fig.3 Fractal characteristics of rough surface

数学家Weierstrass推导出了傅里叶级数形式的Weierstrass函数，之后Mandelbrot将Weierstrass函数应用至分形领域，获得了WM函数。MAJUMDAR等［17］基于WM函数建立了首个应用于实际工程表面的分形接触模型，即MB弹塑性接触模型，这是分形模型的代表。该模型认为临界接触面积只是分形维数和尺度参数的函数，与材料等无关。该模型首先根据WM函数给出了微凸体满足的余弦函数，图4示出微凸体接触示意。

图4 微凸体接触变形Fig.4 Microconvex contact deformation

式中 G——特征尺度参数，mm；

D——分形维数；

l——接触长度，mm。

由式（1）可求得曲率半径R，进一步求出微凸体临界接触面以及单个微凸接触面积和接触载荷，通过对微凸体接触面积和接触载荷进行分段积分，即可得到整个粗糙表面弹性和塑形变形接触载荷和接触面积。

PERSSON［18］基于分形理论和频域变换等数学方法，提出了考虑多尺度效应的统计接触力学理论。该理论模型能够得到不同观测尺度下载荷与接触面积之间的变化规律，更加准确地描述了微凸体的几何形貌。

近年来，国内研究学者在分形接触领域也开展了大量的研究，魏龙等［19］基于分形理论，建立了机械密封摩擦副端面接触模型，得到真实接触面积和接触载荷之间的变形关系。丁雪兴等［20］认为以往对微凸体表征时过于理想化，没有考虑单个微凸体中还含有很多空隙，实际随着变形量的增加，不仅单个微凸体接触长度在增加，该接触长度对应的微凸体幅值及其体积均在增大，且接触长度越大，微凸体中包含的空隙越多，在计算接触面积时使计算结果偏大，对此提出了一个消除空隙误差后的等效接触长度代替原有理论上的接触长度，进一步提高了模型精度。

此外，成雨等［21-24］在分形接触力学建模方面也做了大量工作，刘鹏等［25］基于分形理论建立了改进的分形接触刚度模型。

2 接触界面密封泄漏模型

泄漏造成的负面影响不仅会使设备的性能大幅下降，甚至会造成设备失效，同时还伴随有环境污染等问题。对密封面泄漏机理进行研究是解决密封失效问题的关键，泄漏率或泄漏量作为衡量密封结构密封性能的最直接的定量指标，能够较为准确的描述泄漏程度。下面是几种较为常见的泄漏率模型的计算方法。

2.1 基于分形接触理论密封泄漏模型

HEINZE和MAYER是最早开展机械密封泄漏模型研究的学者之一，HEINZE［26］首先建立了理想光滑平面的机械密封模型，随后MAYER［27］在此基础上，假设两密封面间隙为平行缝隙，对模型进行了泄漏率的计算。上述模型都是假定接触面的表面形貌和工况条件恒定不变，并没有考虑设备在运行过程中密封面微观形貌的随机性变化对密封性能的影响，所得到的泄漏率与真实值之间存在偏差。

孙见君等［28］对锥形密封端面的泄漏率进行了推导，认为流过单位面积的体积流量即为泄漏率，并假设流体在密封间隙的流动状态为黏性不可压缩层流流动，根据流体力学相关知识，径向流动速度满足：

则泄漏率：

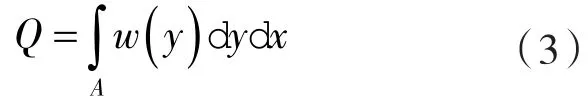
式中 η——流体流动黏度；

h——间隙高度；

A——泄漏通道横截面积；

dx，dy——密封间隙流体的微元长度。

图5示出流体中的一个微元在密封间隙中的流动情况。

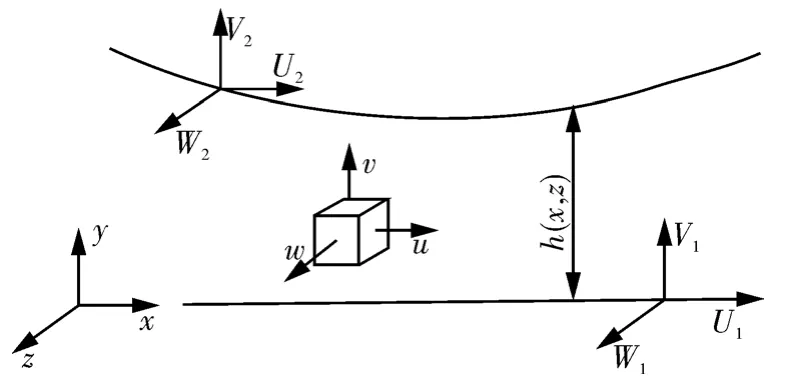
图5 密封间隙流动速度［28］Fig.5 Flow velocity of seal clearance

进一步得到单个泄漏通道的泄漏率：

根据M-B分形接触理论，将式（1）替换式（4）中的h，便可对接触式机械密封的泄漏模型进行分形表征，经过化简为：

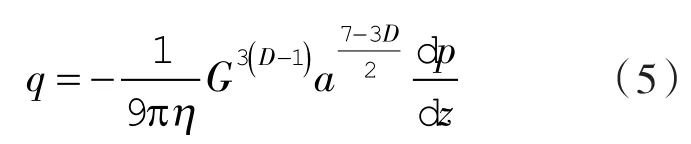
整个密封端面的泄漏率为：

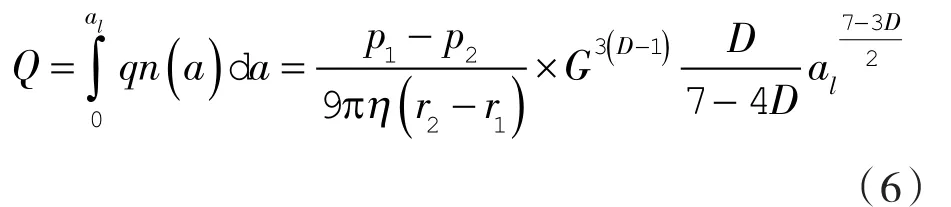
式中 r1，r2——泄漏通道内、外径；

p1，p2——泄漏通道两侧的压力。

通过上述推导可知，泄漏率和流体的黏度、分形参数有关。

冯秀等［29］基于WM分形函数建立了与上述结果类似的螺栓-法兰-金属垫片密封系统密封泄漏模型。孙见君等［30］和李小彭等［31］利用分形理论和Navier-Stokes方程（N-S方程）建立了机械密封泄漏率预测模型，获取了分形参数（D和G）、端面比载荷和材料特性对泄漏率的影响规律。

上述这些模型均未考虑密封界面微动磨损对密封性能的影响因素，进而造成泄漏模型精度不高的弊病。近年来，相继有学者［32-33］基于Archard黏着磨损理论［34］，针对不同的接触式密封结构，建立了考虑磨损的密封模型。李小彭等［35］基于分形理论建立了机械密封界面的磨损模型，分析了密封界面分形参数、材料参数以及工作参数对磨损率的影响，可为后续建立更高精度的密封模型提供指导。

然而，基于分形理论的泄漏模型，对接触模型进行了简化，并且实际接触表面并不一定满足分形特性，而具有分形特性的接触表面也可能只存在于有限个尺度，这些问题均会造成泄漏预测模型与实际值之间的偏差。

2.2 基于多孔介质理论的密封泄漏模型

多孔介质是由固相部分的骨架和非固相部分所占的空间组成，气体、液体或者多相流体可以通过这些孔隙空间形成流动通道。流体在多孔介质中的流动现象和密封界面的渗流现象极为相似，因此，许多学者将密封端面视为多孔介质模型，建立了基于多孔介质理论的密封泄漏模型。

多孔介质模型最早是由FATT［36］提出的，认为多孔介质是由不同直径的管子组成的。顾伯勤［37］认为气体流过多孔介质的流动过程是分子传递和层流过程的耦合，并假设多孔介质各向同性、孔隙空间所形成的流体流道是大量不同半径的弯曲毛细管束，根据Hagen-Poiseuille定律并引入弯曲度系数c得到层流流率公式为：

式中 n——毛细管数目；

ri——毛细管半径；

z——气体黏度；

lm——毛细管的平均长度；

p1，p2——毛细管两端压力。

再由Knudsen公式得到分子流流率：

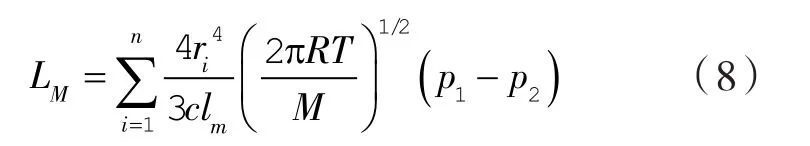
式中 R——通用气体常数；

T——绝对温度；

M——气体的分子量。

将式（7）（8）相加即可得到总的流率，即泄漏率。

文献［38］将密封界面看作多孔介质模型，假设密封端面的介质流动为薄膜流动，在多孔介质模型基础上，对连续性方程和动量方程进行重新推导，得到了用于机械密封端面的流体流动的控制方程，进一步推出静态密封径向泄漏率的解析公式。之后，又有多位学者基于多孔介质模型并结合流体力学理论，对刷式密封系统的流体泄漏特性进行了研究［39-42］。研究表明［43］多孔介质具有分形特性，将分形理论与多孔介质输运特性的研究相结合，来研究多孔介质的流动特性及多孔界面的密封性能成为一种可能。黄晓明等［44］基于分形理论建立了金属垫片泄漏率的预测模型，该模型将泄漏通道视为一束孔径不同的毛细管束，由孔隙率计算得到分形维数，再由分形维数计算出毛细管束的数量，再结合Hagen–Poiseuille方程便可得单个泄漏通道的泄漏量，进一步通过积分即可计算出总的泄漏率

综上所述，基于多孔介质思想的泄漏模型研究，多是将泄漏通道视为一簇毛细管束来模拟流体流动现象，没有考虑这些毛细管之间的相互作用力影响，并且忽略了接触界面微孔的随机分布特性。同时不能保证所有横截面处的微孔其泄漏通道都始终贯穿形成完全的泄漏通道，这会使得计算值总体大于真实值。

2.3 基于逾渗理论的密封泄漏模型

逾渗理论是一种适用于强随机和强无序系统的理论方法［45］。该理论的提出，对研究多孔密封界面这类高度随即且复杂的对象提供了一种新的思路。该理论方法的研究内容是：当系统中的某种成分变化达一定值（逾渗阀值）时，系统的一些物理量会出现急剧变化。

TRIPP等［46］于1981年首次利用逾渗理论来解决密封接触问题，认为接触面积占比达到0.44即为逾渗阈值，低于该临界值，气体泄漏通道将被堵塞，密封良好。PERSSON等［47-48］提出了单枢纽密封理论，利用逾渗理论将接触界面划分为小的栅格，认为密封界面的孔隙会随着放大倍数增大而变多，如图6所示，定义黑色方格为实际接触区域，白色方格为孔隙单元，可以看到在较大观察尺度下，图6（a）中不存在逾渗通道，不会发生泄漏；图6（b）中随着观察尺度变小，孔隙不断增多，直到某一临界观察尺度时，密封界面出现至少一条贯穿界面两端的泄漏通道，流体流经这些通道发生泄漏或渗漏。

图6 二维网格逾渗示意Fig.6 Schematic diagram of percolation in two-dimensional grids

PERSSON等［49］提出发生逾渗时，泄漏率大小取决于泄漏通道最窄的地方即喉部，通过临界放大倍数求得逾渗点尺寸来建立泄漏率的数学模型。目前，绝大多数基于逾渗理论的泄漏率计算模型都是以Persson模型为基础开展的。

BOTTIGLIONE 等［50］基于 Persson接触力学模型和逾渗理论提出了一种新的泄漏率的计算方法，为了准确的估计密封接触面积以及描述粗糙表面，文中还引入了经典的GW接触模型与Persson模型［51］进行对比，得到了相似的规律，验证了模型的正确性。针对目前多数研究对象只是各向同性粗糙表面的问题，文献［52］基于共轭梯度-快速傅里叶变换法确定各向异性粗糙表面的逾渗阈值，并分析了各向异性对逾渗阈值的影响。

近年来，国内学者在基于逾渗思想的接触式密封界面泄漏机理研究方面也开展了大量工作。对于未考虑密封界面有限尺寸效应的问题，史建成等［53］提出了一种栅格渗漏模型，考虑了真实密封界面的尺寸有限性问题，对密封机理和状态演变特性进行研究，通过逾渗特性分析得到不同栅格尺寸和不同接触面积对逾渗概率的影响。李曼利等［54］对不同纹理形状和方向对逾渗特性的影响进行了研究。王衍等［55］基于WM函数对机械密封界面进行了分形形貌表征，结合逾渗理论建立了密封界面泄漏通道模型，揭示了端面比压、分形参数对泄漏率的影响规律。为了使研究对象更接近三维实际，嵇正波等［56］将密封界面在高度方向上也进行了网格划分，研究了不同网格层数对逾渗阈值影响，计算了喉部尺寸，得到泄漏率的数学模型。崔颖等［57］采用了正交实验法，在较少试验次数的前提下拟合接触面积比，根据逾渗理论和自动寻径算法，得到了密封界面泄漏特性规律。

3 研究趋势

随着计算机网络技术的快速发展，人工神经网络也逐渐被应用于泄漏率模型的预测。文献［58］中提出了一种基于因子分析和小波-BP神经网络的天然气管道阀门内泄漏率预测方法。该方法首先通过因子分析实现了阀声发射信号的降维，然后利用小波分解对样本特征集进行分解，最后建立误差反向传播（BP）神经网络模型，对阀门内泄漏率进行定量预测。

同时，数值模拟与仿真技术近年来也得到了大量应用，特别是在分析流体流动特性等方面优势明显，已有文献［59］证明了数值法在计算泄漏率时比推导出来的经验公式更接近于真实值。近年来，许多学者开始将有限元法和计算流体力学结合［42，60-61］，用于预测密封结构的泄漏率。

随着新兴交叉学科的发展，用于研究多孔介质渗流问题的格子玻尔兹曼（Lattice Boltzmann Method，LBM）方法也备受关注，该方法具有介于微观分子动力学和宏观连续性模型的介观模型的特点，能够处理边界条件复杂的非线性流动问题。对比传统的数值研究方法，LBM法对于研究微观密封泄漏通道这类具有高度复杂性和随机性的结构具有明显的优势，并且可以处理多相或者非混相流体流动问题。格子玻尔兹曼方法的提出，构成了联系宏观和微观、连续与离散之间的桥梁，这种介观模型没有对流体介质进行连续性的假设，可对宏观流体参数分布和微观流动细节进行描述［62］，LBM法可以很好地用于分析接触式密封介质的输运特性，未来该方法可能会成为研究密封泄漏机理的一种有效手段和方法。

4 结论

（1）作为泄漏模型的基础和重要组成部分，介绍了Hertz接触模型、统计学接触模型以及分形接触模型等3种经典接触力学模型，对3种模型优略势进行了阐述。

（2）归纳整理了基于分形理论、多孔介质理论以及逾渗理论等3种常见的接触式密封结构泄漏模型研究方法。

（3）针对传统经验公式计算方法所存在的弊病，总结了基于人工神经网络、数值仿真计算和格子玻尔兹曼等3种用于泄漏计算和研究的新方法和新理论，这些总结和探索能够为进一步开展密封性能分析和密封结构设计提供参考。