引入莱维飞行与动态权重的改进灰狼算法

丁瑞成，周玉成

山东建筑大学 信息与电气工程学院，济南 250101

灰狼算法（grey wolf optimization，GWO）是Mirjalili等人[1]通过模拟灰狼种群的社会分级制度与捕猎活动，于2014年提出的一种群智能算法，具有参数简单、易于实现等优点。群智能算法的寻优过程包括两个阶段：前期的全局搜索，初步确定全局最优解最大概率的位置，搜索范围应广泛分布于整个搜索空间；后期的局部搜索，在由全局搜索得到的位置，小范围内进行精细搜索。GWO算法种群位置更新仅由三头精英狼决定，当精英个体的搜索方向存在偏差，种群很难寻优全局最优值，全局搜索能力不足，容易过早收敛。

针对以上问题，相关学者在GWO算法基础上提出改进策略。文献[2]提出一种基于余弦变化的收敛因子与基于步长欧氏距离的动态权重位置更新策略，取得了较好的寻优精度。文献[3]针对GWO易陷入局部最优的问题，对精英个体的位置添加混沌扰动。文献[4]在精英狼的位置引入高斯扰动，增加精英狼跳出局部最优的能力。文献[5]提出一种收敛因子非线性调节策略，提高了寻优精度，但不明显。这些基于GWO算法本身的改进虽然不同程度上提高了算法的寻优性能，但是全局寻优能力有限，算法本身的局限性仍然存在。

不同群智能算法具有各自的优势与不足，相关学者将其他优化算法的搜索策略引入GWO算法的个体位置更新公式，可以更好地改善算法的寻优性能。文献[6]将粒子群算法个体最优机制引入GWO个体位置更新公式，更好地协调了算法的探索与开发能力。文献[7]将差分进化（differential evolution，DE）机制引入精英狼的位置更新公式，基于DE算法较强的全局搜索能力，使种群跳出局部最优值。文献[8]提出一种融合随机蛙跳算法（shuffled frog leaping algorithm，SFLA）的改进GWO算法，通过引入SFLA最差个体的跳跃机制，提高算法的全局探索能力，面对高维复杂寻优函数时，取得了更好的寻优性能。

基于此，本文在改进GWO算法的基础上，引入布谷鸟算法的莱维（Levy）飞行策略，提高了GWO算法的全局寻优能力与收敛精度，尤其面对高维复杂优化问题时，算法依然保持有效性。本文针对GWO算法的改进主要集中在以下3个方面：

（1）引入Singer混沌映射初始化灰狼种群，使初始种群位置在搜索空间分布更加均匀，提高种群多样性。

（2）采用新的非线性收敛因子更新策略，在搜索全期，平衡种群的全局搜索与局部搜索能力。

（3）针对GWO算法位置更新公式仅受精英狼影响，种群容易陷入局部最优的问题，引入Levy飞行策略，降低种群陷入局部最优的风险。并采用一种基于适应度的动态权重策略，提高算法的寻优精度。

1 标准GWO算法

灰狼种群拥有严格的等级制度，体现在GWO算法中，α狼最大程度上决定狼群的行为方式，对应最优适应度的位置，其次是β狼与δ狼，分别对应第2优适应度位置与第3优适应度位置。前三头精英狼负责追踪猎物和引导狼群，其余个体统称ω狼，负责包围与捕杀猎物，在每次迭代过程中依据上一迭代中精英狼的位置信息更新自身位置。在d维搜索空间中，第k只灰狼个体在第t次迭代的位置表示为Xk(t)。精英狼追踪猎物的数学模型表示为：

其中，D为搜索步长；Xp(t)为当前猎物位置；Xk(t+1)为当前个体更新后的位置；A、C为扰动因子，定义如下：

其中，rand()为[0，1]之间的随机数；a为收敛因子，随迭代次数在[0，2]线性递减，定义如下：

其中，T为总的迭代次数。

种群个体在3头精英狼的引导下的位置更新公式如下：

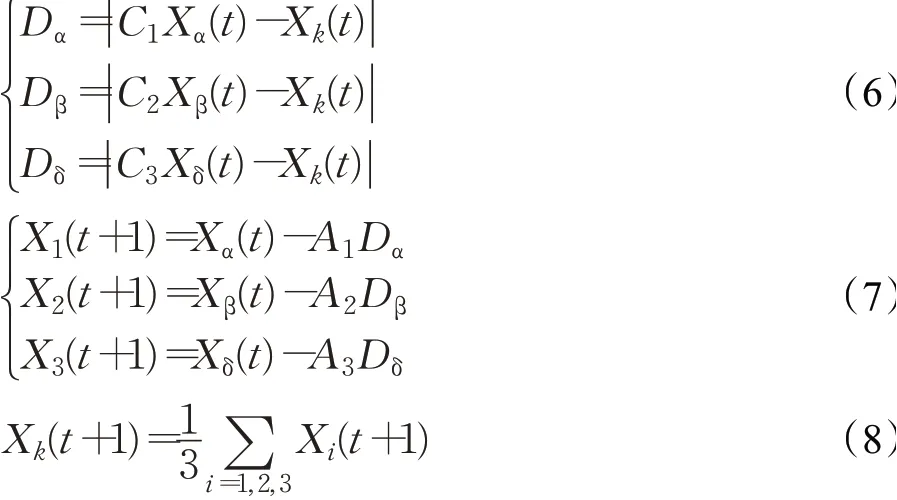
其中，Xα(t)、Xβ(t)与Xδ(t)为当前α、β和δ精英狼的位置；Dα、Dβ与Dδ表示3头精英狼引导下的搜索步长；Xi(t+1)(i=1,2,3）表示灰狼个体在对应精英狼引导后的位置；A1、A2、A3与C1、C2、C3为式（3）、（4）所述扰动因子。

标准GWO算法中收敛因子a采用线性递减策略。由式（3）可知，A取值范围为[-2a,2a]，当||A≥1时，精英狼始终与当前猎物位置保持一定距离并在附近范围内持续搜索，对应于全局搜索阶段。当||A＜1时，精英狼开始引导狼群向猎物位置靠近，对应于局部搜索阶段。扰动因子C取值为[0，2]的随机数，在寻优全期过程中影响种群的搜索方向，从而赋予算法一定跳出局部最优的能力，但是面对复杂寻优问题时存在不足。

2 LGWO算法

2.1 Singer混沌映射

初始种群位置均匀分布于搜索空间，有助于增强算法全局搜索能力，提高搜索效率。标准GWO算法随机初始化种群，存在降低种群多样性的风险，而混沌映射生成的混沌序列，具有遍历性、非线性和不可预测性等特征，常用于替代随机序列初始化种群。本文采用Singer映射初始化GWO种群。作为混沌映射的典型形式，Singer映射具有参数简单，分布均匀等优点[9]，其数学表达形式如下：

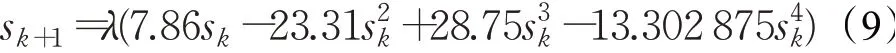
其中，λ∈[0.9,1.08]，Singer映射具有混沌行为。

生成的混沌序列sk∈[0,1]，用于初始化GWO种群位置Xk，如下式所示：

其中，ub与lb为搜索空间的上界与下界。

2.2 非线性收敛因子

标准GWO算法通过收敛因子a调节参数A，从而平衡算法的全局搜索与局部搜索能力。复杂优化问题往往存在多个局部最优值，线性递减的更新策略决定了算法的全局搜索过程仅为全期过程的一半，算法跳出局部最优值的能力较弱。基于此，本文提出一种新的非线性收敛因子更新公式：

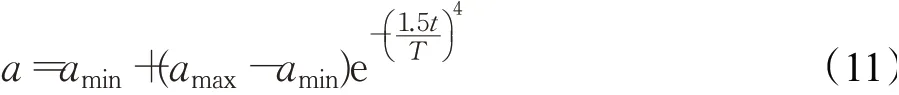
为了验证本文提出非线性收敛因子的优势，列举了文献[5]与文献[10]中的收敛因子更新策略，如下所示：

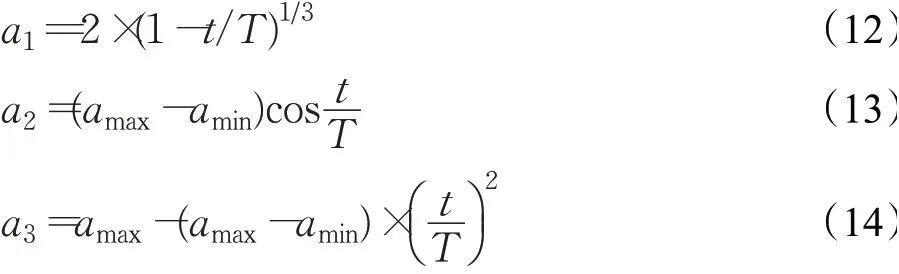
上述非线性收敛因子a的仿真如图1所示。由图1可以看出：与其他更新策略相比，在迭代前期，a取值较大且衰减速度较慢，全局搜索能力较强，促使种群在搜索空间内广泛搜索，有利于避免种群陷入局部最优值。在迭代后期，a迅速衰减至较少的值，局部搜索能力较强，在小范围内精细搜索，有利于加速种群收敛。因此本文提出的非线性收敛因子更新策略可以更好地应用于非线性复杂优化问题的求解。

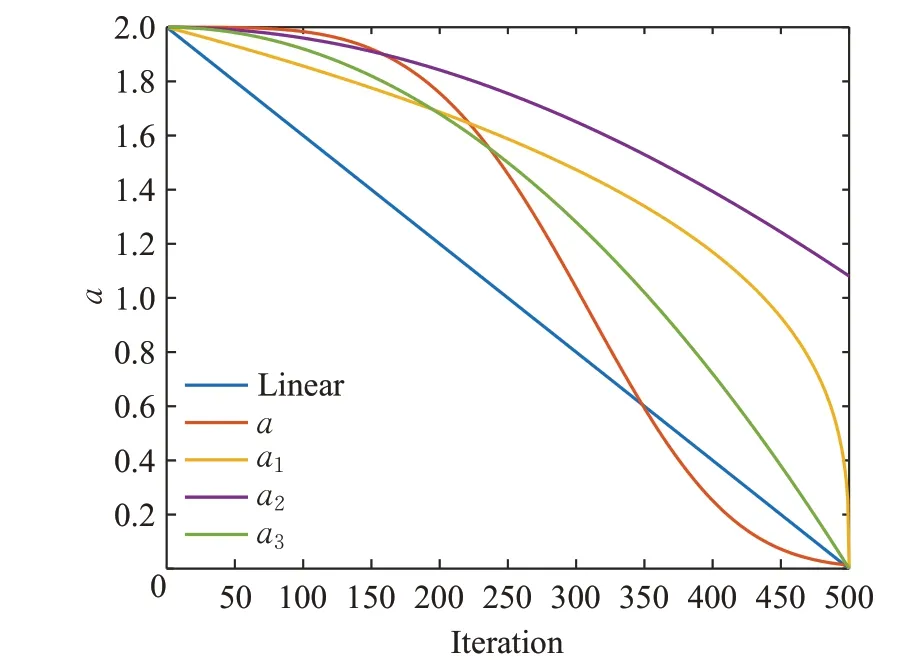
图1 非线性收敛因子曲线Fig.1 Nonlinear convergence factor curve

2.3 引入Levy飞行与动态权重策略

由式（8）可以看出，标准GWO算法种群位置更新公式仅由三头精英狼主导，在搜索过程中，当精英狼陷入局部最优时，种群搜索将陷入停滞。文献[11]提出一种动态权重GWO算法，赋予三头精英狼基于适应度值动态调节的比例权重，取得了更优秀的收敛速度与寻优精度，但是算法跳出局部最优的能力较弱。文献[12]证明布谷鸟算法中Levy飞行策略，可以增强算法的全局搜索能力，其特征是搜索范围远近交替地随机飞行。文献[13]将Levy飞行引入粒子群优化（particle swarm optimization，PSO）算法，避免算法早熟收敛。本文在动态权重GWO基础上引入Levy飞行策略，两种种群个体的位置更新公式如式（15）、式（17）所示。为保证算法在迭代全期的搜索效率，采用贪心算法原则，比较式（15）与式（17）两种个体位置的适应度值，采用适应度更优的个体为最终的更新位置。

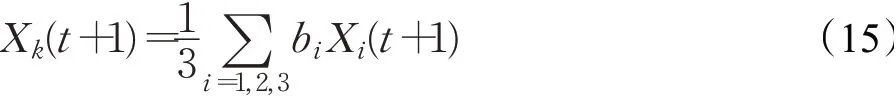
其中，bi(i=1,2,3)为基于适应度的比例权重，如下所示：

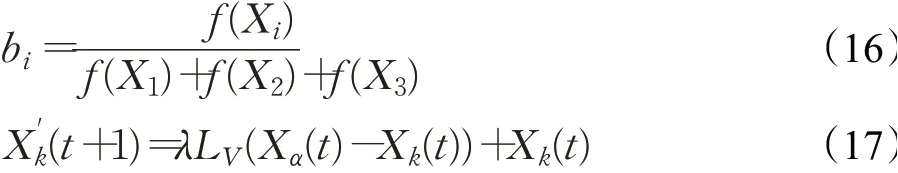
其中，f(Xi)(i=1,2,3)分别表示α、β、δ精英狼在目标函数下的适应度值；X"k(t+1)为采用Levy飞行策略更新后的灰狼个体位置；λ为步长调节系数，受文献[14]的启发，将式（11）的非线性调节策略应用于λ的更新，λmax=1，λmin=0。在迭代前期，较大的λ扩宽Levy飞行在解空间的搜索路径。在迭代后期，较小的λ有利于提高算法的局部搜索能力，加速算法收敛。LV为飞行步长，计算公式如下：

u、v满足正态分布定义如下：

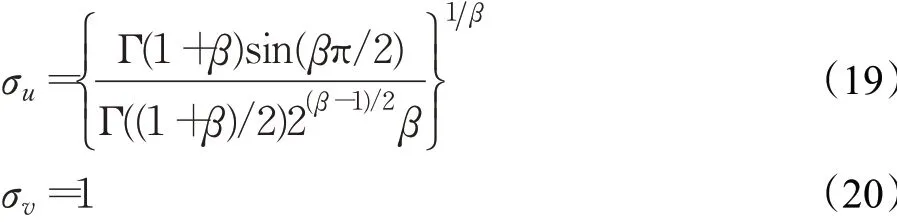
其中，β通常取值于[0，2]之间，这里取值1.5。

2.4 LGWO算法流程

步骤1初始化参数，包括：种群规模N，最大迭代步长T，收敛因子a极值。

步骤2采用混沌映射初始化种群位置，记为：

步骤3计算种群适应度值，依据适应度大小确定α、β和δ狼。

步骤4依据式（11）更新收敛因子a，计算扰动因子A与C的值。

步骤5依据式（15）更新个体位置Xk，计算适应度值f(Xk)。

步骤6更新步长调节系数λ，依据式（17）更新个体位置X"k，计算适应度值f(X"k)。

步骤7比较f(Xk)与f(X"k)大小，若f(Xk)＜f(X"k)，Xk+1=Xk，否则Xk+1=X"k。

步骤8更新迭代步数，判断是否达到最大迭代步长T，满足则输出全局最优值，即α狼适应度值，未满足返回步骤3。

算法1给出了LGWO算法的执行伪代码。

算法1 LGWO算法

Input：

d：the dimensions of the variables，T：the maximum number of iterations，N：population size，ub：upper bounds of variables，lb：lower bounds of variables，f(x)：the objective function

Output：

Xbest：the best solution vector，fbest：the optimal fitness value

1.Initialize the grey wolf populationXi(i=1,2,…,n)by singer mapping and calculate the fitness of each search agent to findXα，XβandXδ

2.Initializea，A，Cand step coefficientλ，then update iteration numbert=1

3.While(t＜T)

4.for each search agent

5.Generate Levy flight step according to equation（18）

6.Update the position of the current search agentXkby equation（15）and calculate the fitnessf(Xk)

7.Update the position of the current search agentX"kby equation（17）and calculate the fitnessf(X"k)

8.iff(Xk)＜f(X"k)then

9.Xk+1=Xk

10.else

11.Xk+1=X"k

12.end if

13.end for

14.Updatea，A，Candλ

15.Calculate the fitness of each search agent and updateXα，XβandXδ

16.t=t+1

17.end while

18.ReturnXbest=Xα，fbest=f(Xα)

2.5 算法复杂度分析

对于标准GWO算法，假设种群规模为N，最大迭代次数为T，自变量维度为d，其时间复杂度为O(N×T×d)[15]，本文提出的LGWO算法主要的执行步骤时间复杂度分析如下：

（1）在初始化阶段，采用Singer映射初始化种群，该阶段时间复杂度为O1(N×d)。

（2）在主循环部分，假设标准GWO算法对于任意灰狼个体在任意维度更新位置的时间为t1，Levy飞行策略更新位置的时间为t2；对于任意灰狼个体，比较适应度优劣并更新位置的时间为t3，则该阶段时间复杂度为O2(N×T×d×(t1+t2)+N×T×t3)，当处理高维优化问题时，时间复杂度可近似等于O2(N×T×d)。

综上所述，LGWO算法的总体时间复杂度为O1+O2=O(N×d+N×T×d)=O(N×T×d)。因此，LGWO算法在标准GWO算法的基础上并没有增加额外的时间复杂度。

3 实验仿真分析

3.1 测试函数及评价标准

为了验证LGWO算法的寻优性能。选用文献[1]中8个国际通用的基准函数用于性能测试，如表1所示。其中，f1～f5为单峰函数，侧重于验证算法的收敛速度与寻优精度，f6～f8为多峰函数，侧重于反映算法跳出局部：最优的能力。仿真实验环境为：Win10 64位操作系统，Intel Core i5-9300H CPU，主频2.40 GHz，内存8 GB，Matlab R2020a。为保证实验公平性，所有实验均独立测试30次，每次总迭代次数T为500次，种群数量N均为30。求取30次寻优精度的平均值与标准差作为性能评价标准。其中，平均值反映算法的寻优精度，标准差反映算法的鲁棒性。以下对比实验均加粗表示评价标准的最优结果。

3.2 算法有效性分析

3.2.1 与标准GWO算法比较

为了验证LGWO算法的寻优性能，分别在低维d=30维，高维（d=100,500维）采用表1所示的8个基准函数进行性能测试，并与标准GWO算法对比。两种算法非线性收敛因子a∈[0,2]。实验结果如表2所示。

表1 基准函数Table 1 Benchmark functions

由表2可知：在低维与高维的所有测试函数中，LGWO算法的寻优精度均优于GWO算法，其中f1、f3、f6、f8收敛至全局最优值0，f2、f4收敛至与0相当接近的寻优精度，f5、f7寻优精度较低，但LGWO算法均优于标准GWO算法，且满足函数的收敛精度要求。对于标准差的测试结果，除了f5、f7，LGWO算法的标准差均为0，表明LGWO具有优秀的鲁棒性。实验结果表明：GWO算法在d=30维下，f1、f2、f7满足函数收敛精度，但在高维100与500维下，GWO算法在所有测试函数均未满足收敛精度要求。相比较LGWO算法，无论在30维与100、500维情况下，LGWO的寻优成功率为100%，均满足函数规定收敛精度，验证了LGWO算法面对高维复杂优化问题时的有效性。

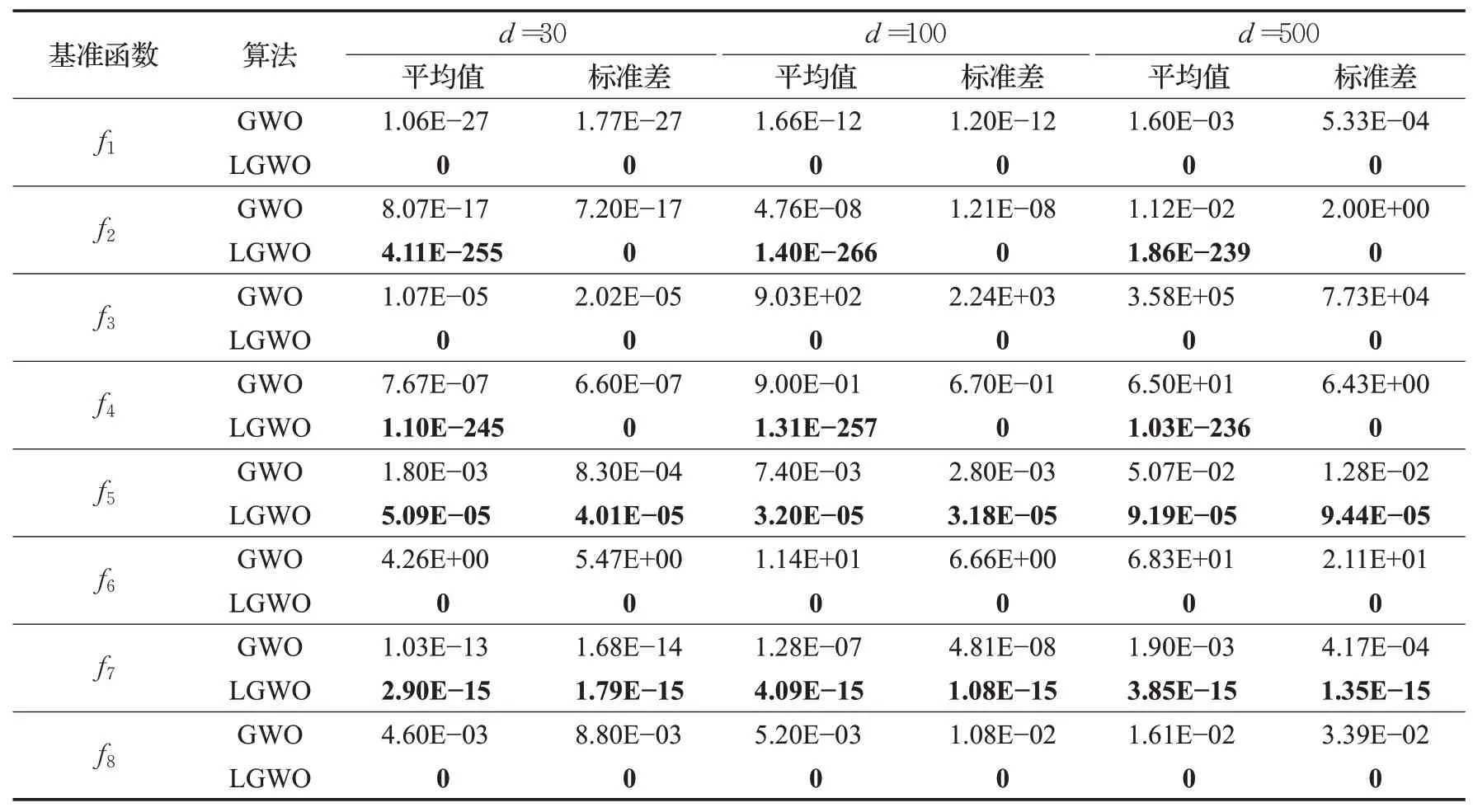
表2 LGWO与GWO测试结果对比Table 2 Comparison of LGWO and GWO test results

图2展示了两种算法在部分单峰函数f1、f2，部分多峰函数f6、f7的适应度变化曲线，更直观地展现LGWO相较于标准GWO算法的优势。由图2可以看出，LGWO整体的收敛速度明显优于标准GWO算法，在f1、f7较早收敛至全局最优值，而标准GWO算法在算法迭代后期适应度曲线陷入停滞，表明算法缺乏跳出局部最优的能力，验证了三种改进策略对于提高算法寻优性能的有效性。

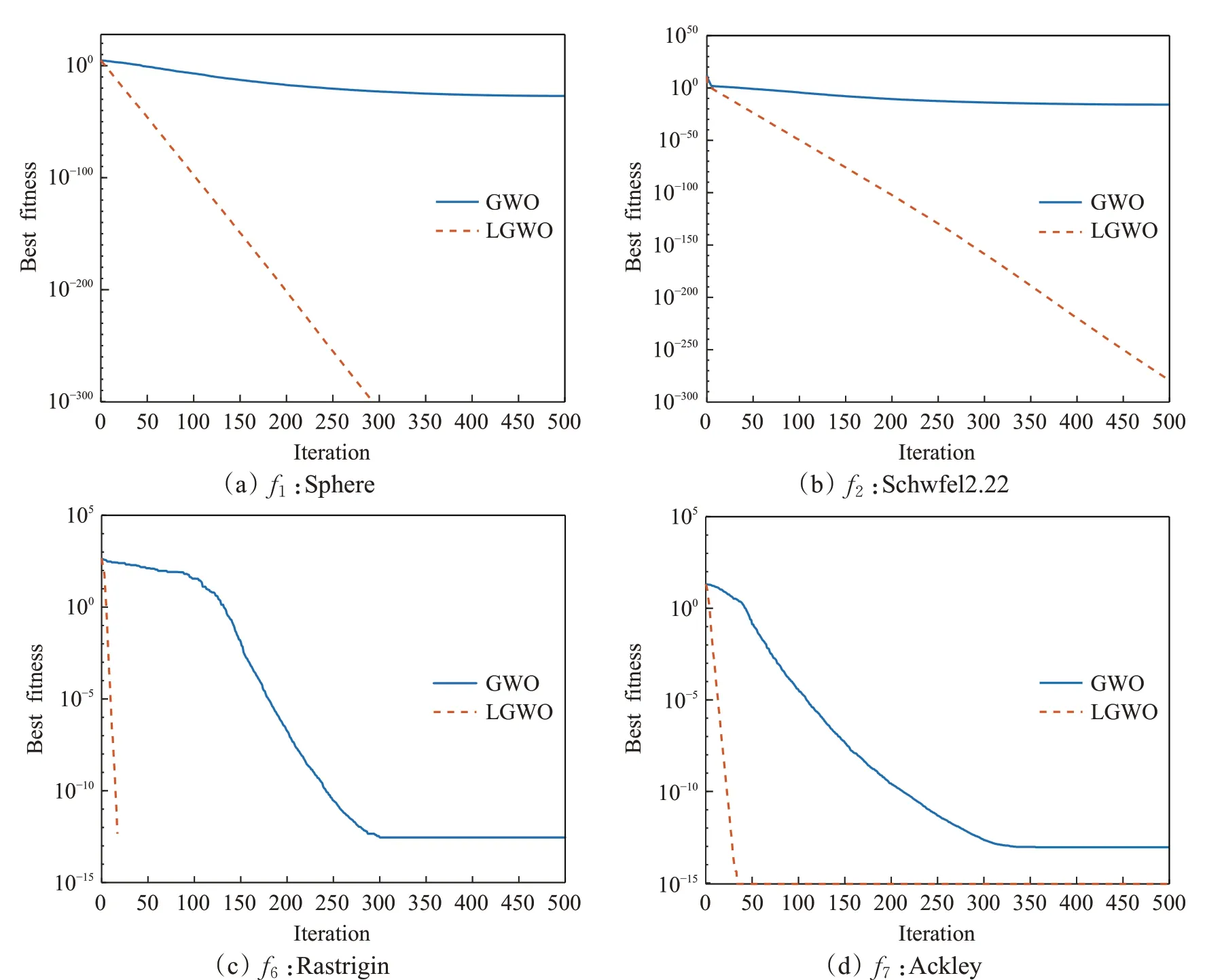
图2 LGWO、GWO适应度变化曲线对比Fig.2 Comparison of fitness curves of LGWO and GWO

3.2.2 与改进GWO算法比较

为了验证LGWO算法改进策略的优势，分别在d=30维度下8个基准函数进行测试，并与文献[5]提出的基于精英个体重选策略与非线性收敛因子的改进GWO算法（EGWO）、基于停滞检测的双向搜索灰狼算法（DBGWO）[16]、融合粒子群算法的改进灰狼算法（PSO-GWO）[17]进行对比。为了实验对比的公平性，对比算法的实验结果均来自原参考文献。

由表3可以看出，在低维d=30维条件下，LGWO在所有测试函数中寻优成功率为100%。在多峰函数测试中，对于f7，NGWO算法取得了最优寻优精度为4.40E-16，而LGWO算法的寻优精度为2.90E-15，两者仅相差1个数量级。对于f8，EGWO算法与PSO-GWO算法的寻优精度下降明显，仅为4.99E-04与9.00E-04，表明这两种算法的改进策略虽然一定程度上提高了GWO算法的全局搜索能力，但是并非在所有测试函数适用，存在局限性，而DBGWO算法与LGWO算法均收敛至理论最优值0。综合分析，LGWO算法在多峰函数测试中取得了优秀的寻优性能，验证了该算法具有较强的全局寻优能力。

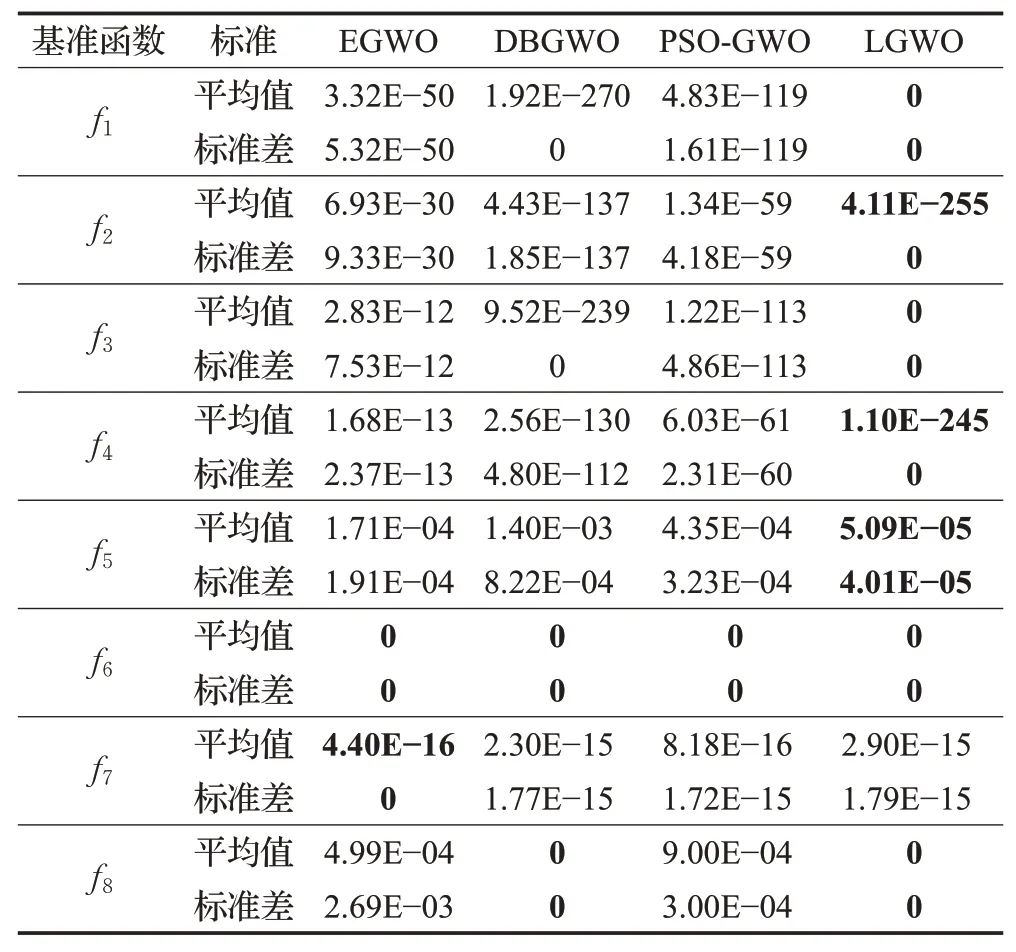
表3 4种GWO改进算法寻优结果比较Table 3 Comparison of optimization results of four GWO improved algorithms

在f1～f5的单峰函数测试中，LGWO算法在所有函数均取得了最优的寻优精度与标准差。对于f5，LGWO取得5.09E-05的寻优精度，在四种算法中最优且唯一满足函数收敛精度。从f1～f4可以看出，三种对比算法的寻优精度由高到低依次为DBGWO算法、PSO-GWO算法与EGWO算法，LGWO算法寻优精度明显优于3种对比算法，验证了本文改进策略有效提升了标准GWO算法的收敛精度。

针对标准差的实验结果，LGWO算法除了f5、f7，在其他函数的寻优精度保持稳定，并在所有测试函数中取得最优的标准差，表明LGWO算法面对复杂优化问题依然保持有效性，具有良好的鲁棒性。

3.2.3 与其他优化算法比较

为了进一步验证LGWO算法面对高维复杂优化问题的有效性。在维度d=100维下，选取表1中8个基准函数进行实验，并与混合策略改进的鲸鱼优化算法（MSWOA）[18]、基于协同进化的动态双重自适应改进PSO算法（DDAPSO）[19]、基于曲线自适应与模拟退火的蝗虫算法（SA-CAGOA）[20]进行性能对比。为了保证对比实验的公平性，各个算法的参数设置均来源于原文献，MSWOA算法非线性调节系数取2；DDAPSO算法惯性权重取值范围[0.4，0.9]，学习因子取值范围均为[0.5，2.2]，混沌参数为4；SA-CAGOA算法初始温度为100，结束温度为1，退火系数为0.95，玻尔兹曼常数为10，曲线自适应参数范围取[0.000 01，1]。实验的对比结果如表4所示。

由表4可以看出：在高维d=100维下，LGWO算法除了多峰函数f7，在其他函数的测试中均取得了最优的寻优精度与标准差，且均满足函数收敛精度。在函数f7中，LGWO算法收敛于4.09E-15，与MSWOA算法取得的最优精度8.88E-16接近。综合分析，3种对比算法的寻优精度由高至低依次为：MSWOA算法、SA-CAGOA算法与DDAPSO算法。DDAPSO算法在所有测试函数的寻优精度平均值均不满足收敛精度要求，表明该算法全局寻优能力不足，缺乏跳出局部最优的能力，容易过早收敛。MSWOA算法的寻优性能明显优于DDAPSO算法与SA-CAGOA算法，在多峰函数f6与f8中收敛至理论最优值0，但对于单峰函数的收敛精度与LGWO算法存在一定差距，比如在f2中，寻优精度仅为2.09E-137，而LGWO算法取得了1.40E-266。

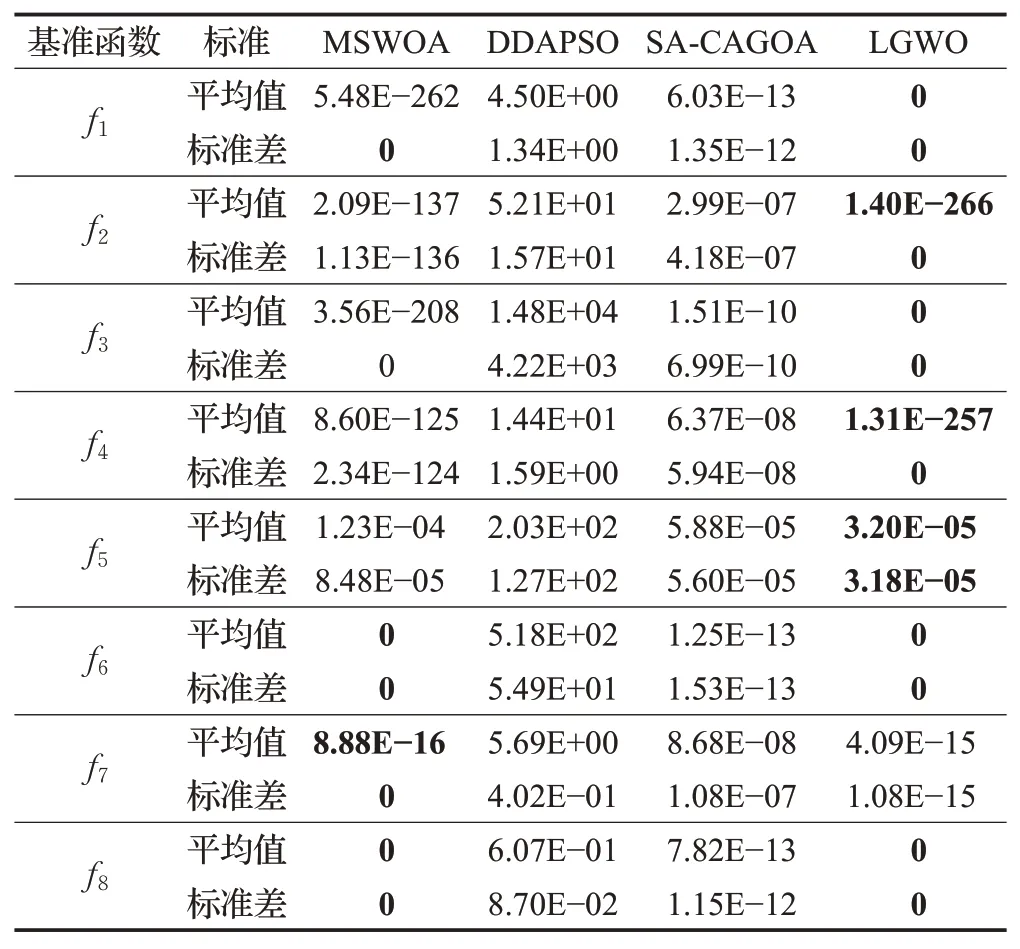
表4 4种优化算法寻优结果比较Table 4 Comparison of optimization results of four optimization algorithms

图3给出了4种算法在函数f2、f4、f6、f7的适应度变化曲线。可以看出面对高维复杂优化问题，DDAPSO算法无论面对单峰函数还是多峰函数，寻优性能均受到很大程度的抑制，在迭代初期种群已陷入停滞，无法跳出局部最优解。SA-CAGO算法稍优于DDAPSO算法，但从f6、f7的收敛曲线可以看出与LGWO算法与MSGOA算法存在差距，两者收敛速度与收敛精度均优于SA-CAGOA算法。MSWOA算法的全局寻优能力较强，仅次于LGWO算法，但在多峰函数f6与f7中收敛速度不如LGWO算法，并在单峰函数f2与f4中，在迭代前期，算法的全局搜索基本陷入停滞，在迭代后期才开始收敛于全局最优值，而LGWO算法随迭代次数稳定向全局最优值收敛，验证了LGWO算法求解高维复杂寻优问题时的优势。

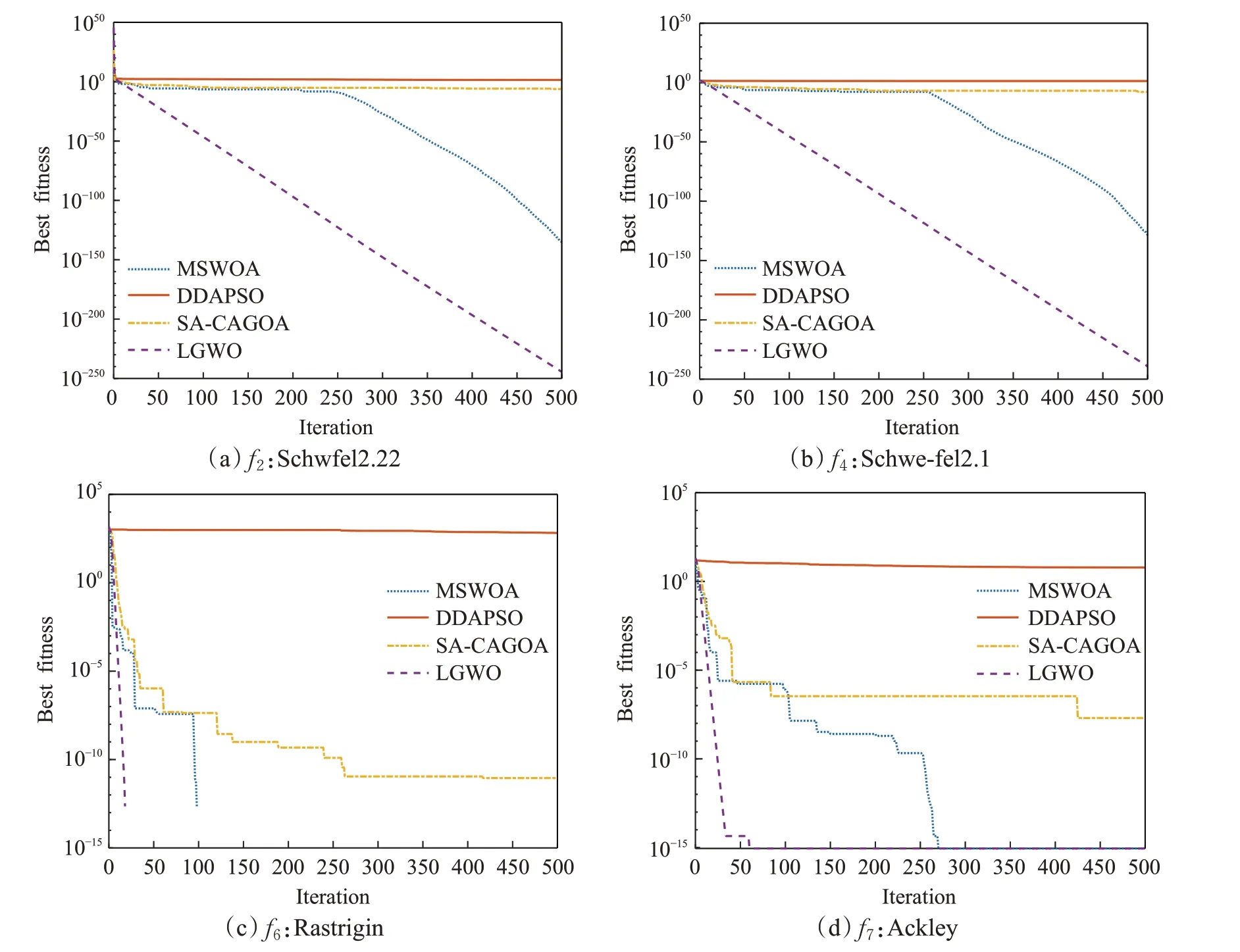
图3 4种优化算法适应度曲线对比Fig.3 Comparison of fitness curves of four optimization algorithms

3.3 三种改进策略分析

为了分析LGWO算法三种改进策略对于GWO算法的影响。将采用改进混沌映射的GWO算法（CGWO）、采用非线性收敛因子的GWO算法（NLGWO）与采用新的位置更新方程的GWO算法（PGWO）在8个基准函数（d=30维）上进行实验对比。对比结果如表5所示。

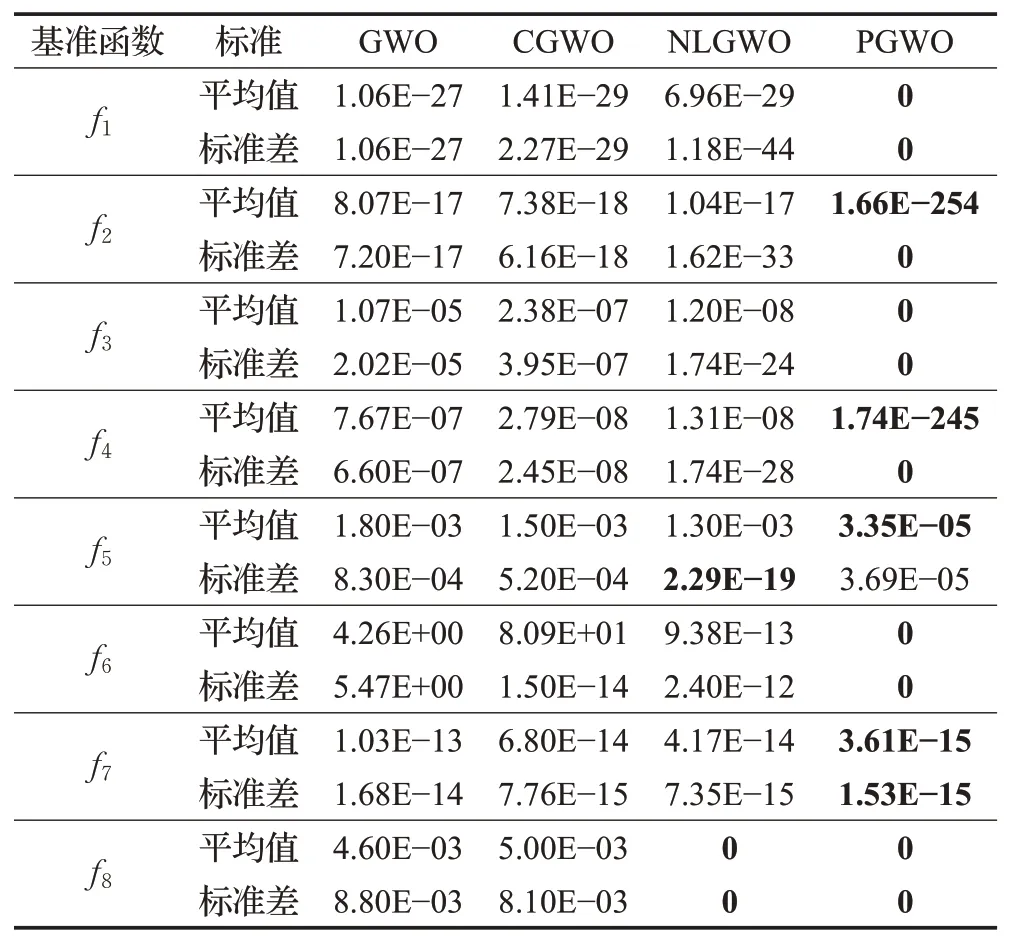
表5 三种改进策略实验对比Table 5 Comparison of three improvement strategies

由表5可知，引入混沌映射的CGWO算法相较于标准GWO算法，寻优精度与标准差有一定的提升，但是提升不明显。表明种群初始均匀分布于搜索空间，在迭代前期，一定程度上提高了算法的搜索效率，但是在迭代后期对于算法性能的提升不大。NLGWO相较于CGWO性能更加优异，在求解多峰函数f6、f8时满足函数收敛精度要求，尤其在f8收敛至理论全局最优值0。可见收敛因子非线性调节策略更适用于求解复杂优化问题，前期与中期较大的收敛因子增强了算法的全局搜索能力，更大概率发掘全局最优值；后期较小的收敛因子提高了算法收敛速度与精度。但是NLGWO在其他测试函数中对于算法寻优精度没有明显提升。引入新的位置更新策略的PGWO算法在f1～f4、f6、f8的测试中的寻优精度平均值明显优于其他算法，在f5、f7中，PGWO算法寻优精度稍好于其他算法，并且满足函数的收敛精度要求。对于标准差的测试结果，PGWO算法除了f5，标准差均为0，可见PGWO算法除了拥有优异的寻优精度，也具有较强的鲁棒性。实验结果表明：基于适应度的动态权重与Levy飞行的位置更新策略对于标准GWO算法的寻优性能有较大的提升。

4 结语

针对标准GWO算法全局搜索能力不足，易陷入局部最优等问题，本文通过Singer混沌映射初始化种群，提高算法搜索效率；引入非线性收敛因子更新策略，提高算法前期全局搜索能力与后期收敛速度；采用基于适应度的动态权重位置更新策略，提高寻优精度，并与Levy飞行相结合，避免种群过早收敛。仿真实验表明LGWO算法的寻优精度与收敛速度有了较大的提升，并验证了LGWO算法求解高维复杂优化问题时的有效性与优秀的鲁棒性。