基于外形不确定性的热防护系统概率设计

张 凯，石钊旭，郑小鹏，许 诺，陆 规

（1. 中国运载火箭技术研究院，北京，100076；2. 华北电力大学，北京，102206）

0 引 言

热防护系统的作用为保护飞行器在高速状态下顺利经过大气层，防止飞行器表面产生的气动热影响飞行器内部仪器安全运作，其可靠性和结构完整性对飞行器的安全至关重要。在对热防护系统的稳健设计过程中，传统方法通常假设所有可能影响飞行器安全的因素最坏情况同时发生[1]，而不考虑该种情况发生的可能性大小。在热防护系统不断趋于轻质化、一体化发展的当下，这种设计方法显得过于保守与低效。因此，为了提高飞行器性能、减轻飞行器的重量，必须为热防护系统提供更加精细与高效的设计方法。

在热防护系统设计阶段，系统的不确定性主要包括零件制造安装过程中产生的尺寸偏差、外部环境变化造成的气动热变化和材料因温度变化性能的不稳定等。为掌握设计参数特性，在保证安全的情况下尽量减少设计的保守性，就要开展更加精细化的设计[2]，尽可能多地将重要的不确定性因素考虑进来。概率化是精细化设计的一种重要方式，概率化设计方法是采用概率的方法对随机不确定性参数进行量化，在给定输入的不确定信息下，估算出输出响应的不确定性。采用概率设计方法能在保证可靠性的前提下有效降低系统重量[3]。

目前概率化设计的不确定性输入主要包括以下方面：a）热防护系统材料属性的不确定性。Howell[4]最早提出利用蒙特卡罗方法对热传导参数的不确定性进行分析，奠定了不确定性概率化设计的基础；辛健强、屈强等[5,6]考虑了二维多层热防护系统的各层厚度、材料热导率、比热容、密度和涂层材料辐射率等参数不确定性对系统背温的影响。b）来流环境的不确定性。Weaver[7]通过CFD数值模拟方法，研究了来流的速度、温度和密度以及碰撞系数对飞行器气动热和流场的影响；何忠骏[8]利用随机过程展开方法考虑了来流热载荷不确定性对二维盖板式热防护系统的影响；张伟[9]从来流速度、来流温度、壁面温度和来流密度这四个不确定性方面，对返回舱开展了气动热不确定性量化分析和敏感性分析；邬晓敬等[10]研究了飞行状态参数（马赫数、仰角）的不确定性对翼型气动热特性的影响。

现有概率化设计模型方法，大多没有考虑几何形状的影响，仅针对简单二维几何模型，热量传导简化为一维[11]或者二维[5,6]。而对于目前一体化大面积精细设计实际工程应用来说，只取其中微小单元做分析，简化成一维或二维模型，无法体现成体的热防护性能。本文针对球头、平板、锥体三种典型飞行器形状，构建三维真实模型，比较与二维模型差异，同时研究不同外形下，来流热流以及材料热物性参数等概率特性分布在热防护系统设计中的传播特性。

1 概率化设计流程

在前人工作基础上[12,13]，结合本文工作实际，本文所提出的不确定性设计主要包括以下流程，如图1所示。

图1 不确定性概率设计优化流程 Fig.1 Uncertainty Probabilistic Design Optimization Process

a）对系统进行确定性建模，在该基础上考虑系统中的不确定性参数与变量，根据热防护系统真实环境决定性能与构型需求，多层热防护系统的不确定性涉及到多种因素，其中最重要有3种：物性参数、热流密度、几何外形，选取这3种因素作为系统不确定性来源，实现各不确定性参数的区间表达；

b）对这些不确定性参数进行灵敏度分析，将有显著影响的参数输入到模型中，进行不确定性建模；

c）由于高精度模型的计算成本较大，效率较低，代理模型具有快速模拟且拟合精度较高的特点，可以通过构建代理模型对原来的高精度模型进行近似，以此作为高精度模型的快速低成本替代，本文采用的是响应面的代理模型；

d）通过代理模型的计算结果以及采用拉丁超立方抽样方法的蒙特卡罗模拟[14]来对不确定性进行分析，如：定量分析系统性能在不确定性影响下的分布特征、计算设计方案的可靠度[15～17]等；

e）通过敏感度分析[18]，对系统进行不确定性优化，使得系统最终符合设计要求，本文采用的敏感度分析方法为相关系数法。

2 有限元概率分析方法

2.1 有限元理论模型

有限元分析[19]（Finite Element Analysis，FEA）采用数学近似的方式，模拟实际物理系统（几何和载荷工况），其主要思想是把系统划分为有限数量的简单且相互作用的单元，用这些有限数量的未知量去逼近无限未知量的真实系统。有限元拥有计算精度高和适用于各种复杂形状的特点，因此被当作是一种非常有效的工程分析手段。

三维瞬态热传导方程可以表达为

上表面受到气动加热，边界条件为

下面表面当作绝热壁面，边界条件为

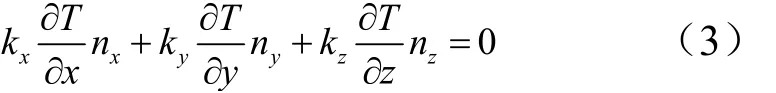
初始时刻，热防护层温度分布：

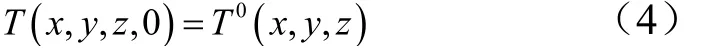
式中ρ为材料密度；c为材料比热容；τ为时间；kx，ky，kz为材料沿物体3个主方向的热导率；nx，ny，nz为边界外法线的方向余弦；h为对流换热系数；Ta为外部环境温度；T0为热防护层初始时刻温度；T为温度，是时间与坐标的函数。一阶常微分方程经由偏微分方程离散后得到：

式中C为热容矩阵，K为热传导矩阵，C和K都是对称正定阵；P为载荷向量；T为节点温度向量；T˙为节点温度对时间的导数向量。上述方程的求解利用直接积分法完成。

2.2 模型验证

对本文提出的有限元模型进行验证，采用文献[5]中数据，进行模拟得到背温曲线对比如图2所示，最大误差不超过1.35%，模拟结果与论文数据拟合良好。

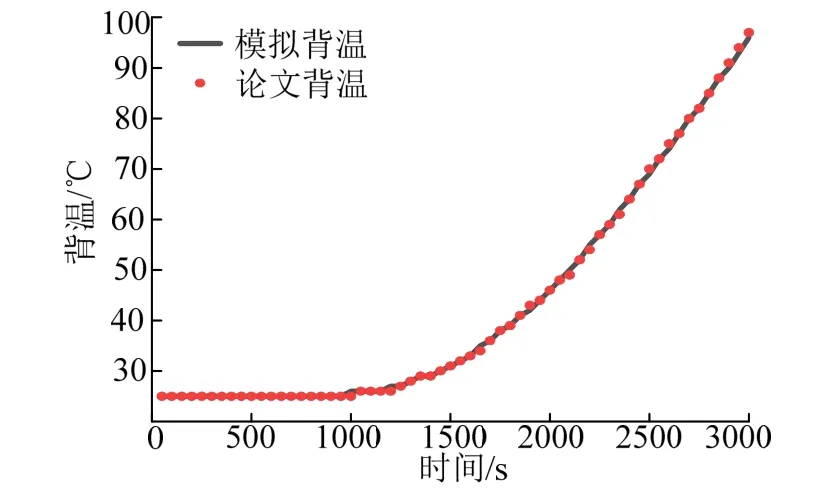
图2 有限元模型背温验证 Fig.2 Finite Element Model Back Temperature Verification

2.3 三维模型与二维模型对比

在热防护系统概念设计中，经常将热防护系统实际模型简化，现对热防护系统经常用到的3种外形，利用2.1节所述方法建立三维典型飞行器有限元模型。模型几何尺寸如图3所示。取球头模型中微小单元，锥体与三维圆环截面建立二维有限元模型，模型尺寸如图3b所示。

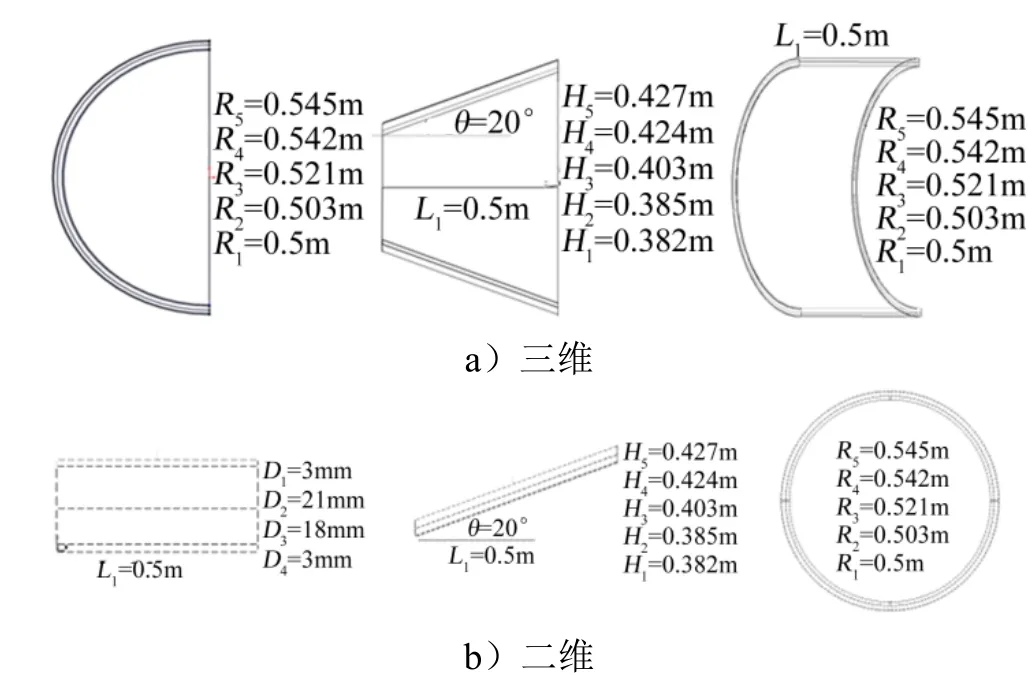
图3 球头-锥体-圆板几何尺寸 Fig.3 Geometry of ball Head- Cone - circular plate

在所建立的有限元模型中，采用辐射式多层盖板热防护系统[5,20]，其中第1层为盖板防热层，厚度为 3 mm，第2层和第3层分别为高温隔热层、低温隔热层，厚度分别为21 mm、18 mm，第4层为蒙皮结构层，厚度为3 mm，各层材料物性在表1中给出。

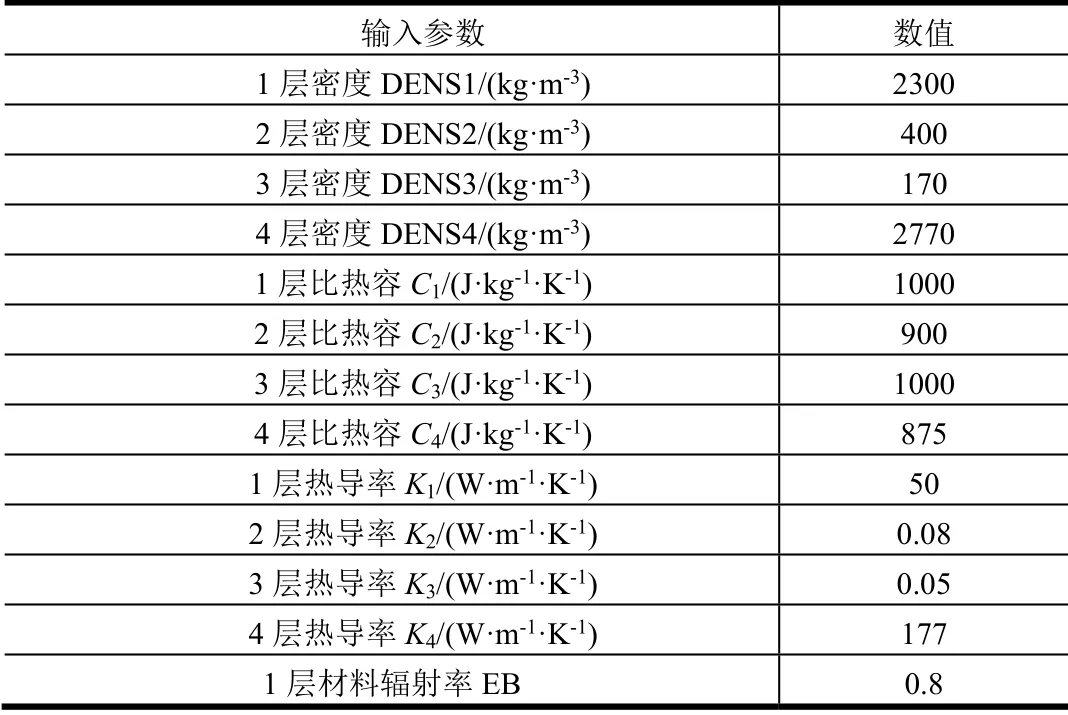
表1 确定性输入参数 Tab.1 Deterministic Input Parameters

图4为气动热和背温时间变化历程。采用图4a的气动热通量，不同外形下热防护系统背温的时间变化历程如图4b所示，三维圆环与二维圆环背温在最终时刻分别为104.77 ℃与104.68 ℃，可见若忽略高度方向热传导的情况下，可近似简化为二维模型。三维锥体与二维斜面背温平均值在最终时刻分别为127.22 ℃与121.28 ℃，相差约6 ℃，三维球头与微单元背温在最终时刻分别为105.2 ℃与97.67 ℃，相差7.53 ℃。相比于规则对称的圆环结构，非规则的椎体及球曲面导致传热热流方向发生偏转，固与二维模型预测结果发生偏离。在考虑锥面与弯曲球面的辐射角度以及热流密度非均匀等因素下，传统任取微小单元做一维传热分析具有一定的局限性。整体由瞬态热分析结果可以看出热防护系统的防隔热性能良好。

图4 气动热和背温时间变化历程 Fig.4 Time Evolution of Aerothermal Curve, Back Temperature

续图4

圆形与锥形沿热防护层厚度方向温度随时间变化如图5所示。两种外形热防护层上表面受到气动热的影响导致两者表面温度相同，但是随着时间推移，锥形沿热防护层厚度方向温度提升比圆形形状更快，说明不同外形对热量传递的速度有影响。

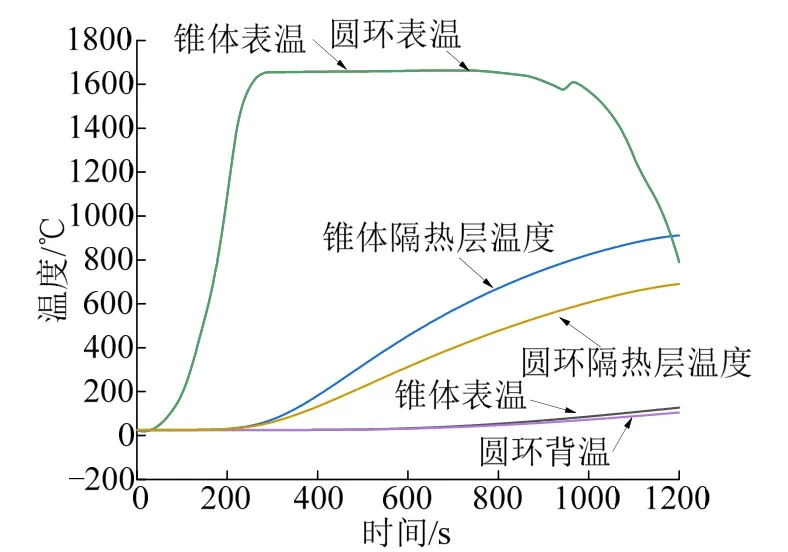
图5 锥形与圆形厚度方向温度历程 Fig.5 Temperature Histories in the Thickness Direction of Cones and Circles

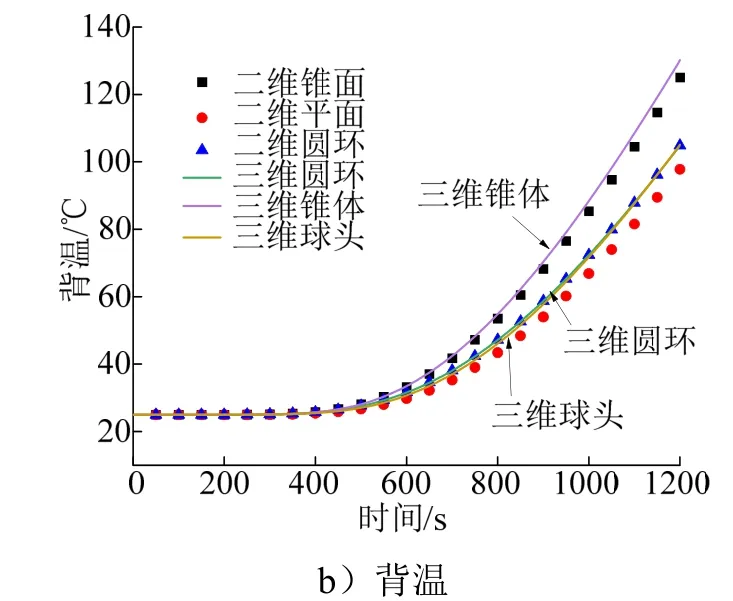
在三维模型中，锥体的背温提升速率大于球层与圆板形状的速率。图6为终末时刻3种外形沿热防护厚度方向的温度柱状图。

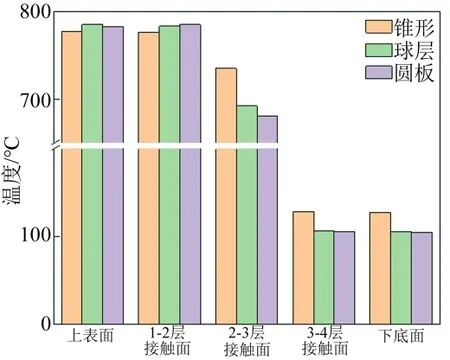
图6 终末时刻3种外形温度分布 Fig.6 Temperature Distribution of Three Shapes at the End Time

由图6可以看到，锥体在高温隔热层与低温隔热层接触面的温度远大于另外两种形状，导致背温沿厚度方向的温度梯度加剧，背温高于另外两种形状。

2.4 不同外形下物性参数不确定性对背温的影响

在热防护系统分析与设计中，存在着诸多不确定因素如几何装配偏差、实际加工制造误差、材料物性也会因温度的变化发生显著变化等，从数学统计学上来讲大致服从一定的数学分布规律，将这些服从某种数学分布的不确定性因素看做输入，进行相关概率分析可得到目标函数概率信息。

选取几何参数及物性参数，假设各参数服从截断高斯分布随机性分布，标准差遵循3σ原则[21]，误差上下限为5%，设置底层蒙皮结构温度作为输出，各变量所代表的物理意义如表2所示。

表2 不确定性输入参数 Tab.2 Uncertainty Input Parameters

经拉丁超立方抽样蒙特卡洛模拟172次后，建立响应面，拟合出响应面后便可运用响应面方程代替实际有限元计算过程进行计算，计算效率将会大大提高。利用响应面模拟100 000次得到不同外形下影响背温的灵敏度如图7所示。

通过灵敏度分析可得到相关系数对系统输出参数的影响程度。由图7可知，盖板式热防护系统影响输出变量最大的前4个输入变量分别是D2、D3、K2、K3，即不同外形热防护层的高温隔热层与低温隔热层的厚度与材料热导率的不确定性对背温影响显著，3种外形高温隔热层的厚度占比都在16.6%左右，对盖板式热防护系统到达底层的最高温度影响最大，且是负相关。低温隔热层厚度近似占比为16.1%，其次是高低温隔热层材料的热导率占比为9.6%与9.0%，且只有K2、K3正相关，对于底层蒙皮最高温度越低越好的热防护系统来说，应尽量通过增加负相关变量参数值或降低正相关变量参数值来达到降低底层蒙皮最高温度的效果。

图7 灵敏度分析 Fig.7 Sensitivity Analysis

其中圆板的低温隔热层热导率占比为10.33%，较高于另外两者，其余参数对热防护性能的影响所占比例不大，均为6%～8%。故在盖板式辐射多层热防护系统结构设计和制造中为提高系统的可靠性，应当尽量控制高温、低温隔热层材料热导率物性的稳定，不因其他因素变化而产生波动，在制造时减小防护层厚度的偏差，控制在尽量小的误差范围内。

3 热可靠性评估

3.1 可靠度定义

热防护系统的热可靠度定义[22,23]为

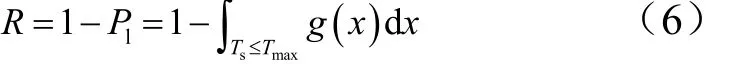
式中Pl为热防护系统性功能失效概率；Ts为内基体所能承受许用温度；Tmax为背温随时间历程中温度最大值；g（x）为不确定因素作为输入变量服从的概率密度函数。

本文采用蒙特卡洛法，可靠度经大量模拟可直接从统计输出结果得到：

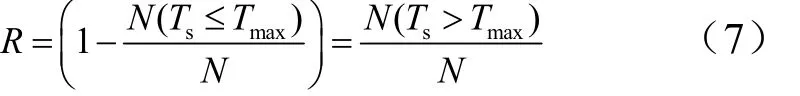
式中N为蒙特卡洛法模拟的次数。

采用概率方法时，需要结合工程实际对系统鲁棒性进行评估并设置相应可靠度范围，经设计后得到系统可靠性在范围内，则结束当前阶段设计，若不在可靠性范围内则可调整隔热材料厚度，重新进行概率设计流程，直到满足要求。

3.2 概率设计方法的收益

设置蒙皮以下机内设备耐受温度为150 ℃，对比传统裕度设计与概率设计的结果。依据以往安全裕度设计要求，将各不确定因素考虑到最坏情况，建立确定性模型，进行有限元计算。先前盖板式热防护系统的尺寸如表3所示。

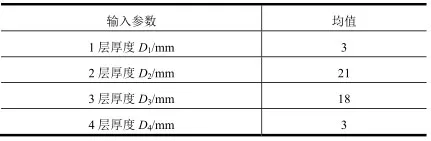
表3 传统式盖板系统尺寸 Tab.3 Traditional Cover System Dimensions

选取盖板式热防护系统厚度t（D2+D3）作为设计参数，以每增加1 mm厚度选取1个点，共选取6个厚度参数点分别构造确定性模型，模型中其他不确定因素均选取对底层蒙皮经历最高温度最不利的情况，以此进行计算，统计底层蒙皮1200 s内所经历最高温度Tmax数据，如图8a所示。

依据概率设计过程，考虑各不确定因素在取平均值的情况下，建立确定性模型，进行有限元计算。依据前面灵敏度分析结果，选取盖板式热防护系统灵敏度分析中对底层蒙皮经历最高温度影响最大的参数隔热层厚度D2+D3作为设计参数，选取对系统输出参数Tmax影响最大的参数D2+D3作为设计参数可以迅速且有效地获得最优解。运用设计参数在35～45 mm范围内每隔2 mm取1个点，分别建立确定性模型进行计算，统计1200 s内底层蒙皮经历最高温度maxT数据，绘制成曲线，如图8b所示。从图8大致估算各因素不确定性影响温度范围，初步确定设计参数D2+D3=38 mm，即maxT=132 ℃时所对应D2厚度值。依据可靠性要求，在系统机内设备耐受温度为150 ℃的情况下，考虑各种不确定性因素，该热防护系统须达到99.999%的可靠度。

将设计参数t=38 mm带入确定性模型，运用参数化建模，建立参数化模型，考虑各不确定因素的不确定性，设置输出参数，进行样本计算。通过样本结果拟合响应面，并模拟抽样100 000次，统计抽样结果。统计出连接部位底层蒙皮经历最高温度的累积分布曲线，如图8c所示。maxT≤150 ℃的概率在86%左右，故调整设计参数D2+D3，将D2+D3调整为39 mm，重新带入确定性模型进行迭代计算，直到可靠性满足要求。

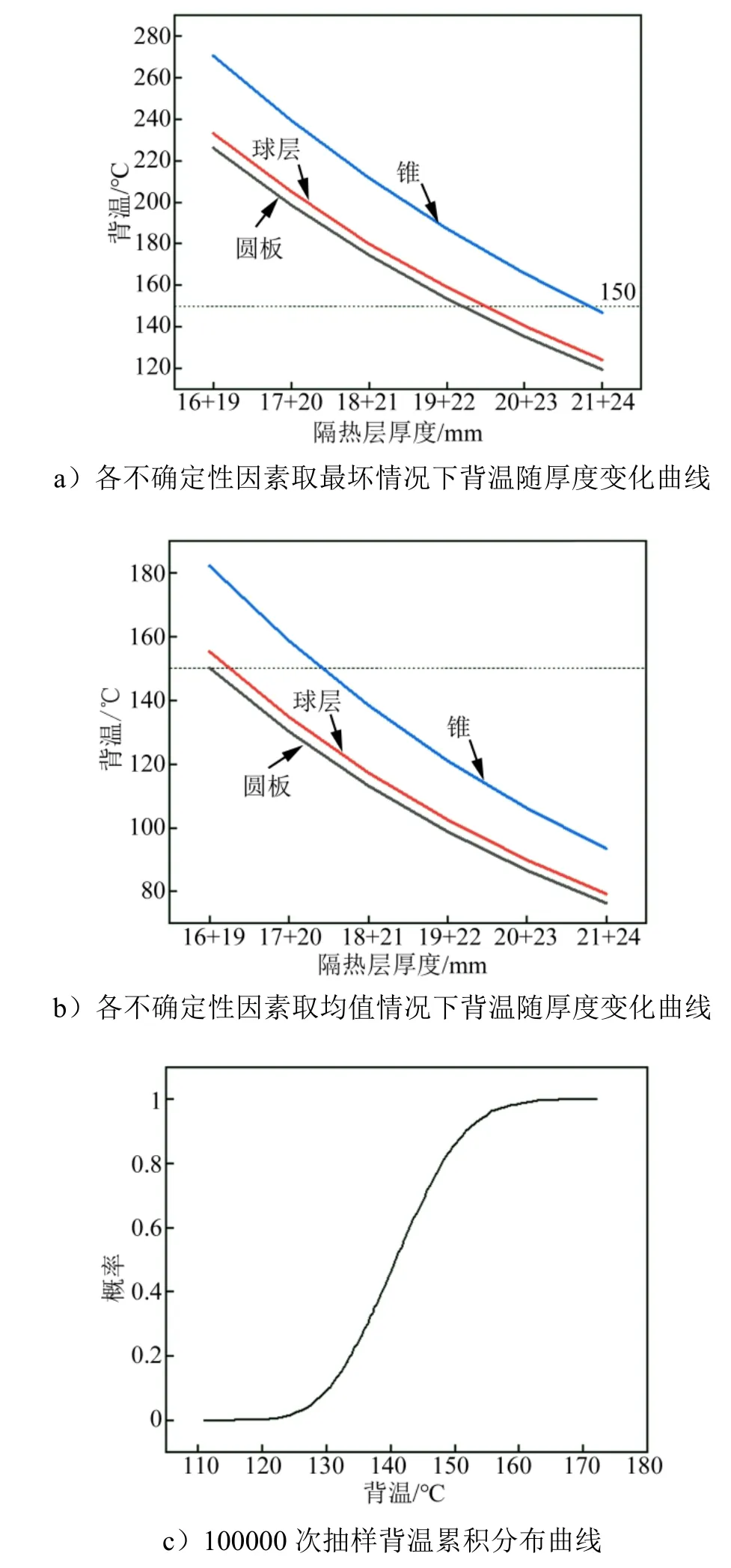
图8 热防护设计 Fig.8 TPS Designs

蒙皮以下机内设备耐受温度为150 ℃，即sT=150 ℃时对应的热防护系统厚度。将各不确定性因素考虑到最坏情况，即制造尺寸、比热容、密度、发射率等取偏差最小值，热导率取偏差最大值，由图可得传统设计尺寸，并重新带入模型进行验算得到新设计的盖板式热防护系统尺寸如表4所示。

表4 新设计的盖板式热防护系统尺寸 Tab.4 Newly Designed Cover Plate Thermal Protection System Dimensions

4 结 论

本文对不同外形热防护系统物性参数与热流的不确定性等角度对辐射式多层热防护系统进行了研究，得到以下结论：

a）三维与二维模型之间存在差异，若三维模型沿宽度方向无限长，且沿宽度方向没有发生形状变化，可近似简化为二维模型，但简化后的模型与三维模型仍有差异，热防护系统仅从二维模型进行设计，还存在较大的不足。

b）不同外形对热量传递也存在影响，在沿宽度方向形状变化越剧烈的外形会造成更大的温度梯度，导致热量传输更迅速，在本文研究里锥形背温提升率大于球层大于圆板。

c）3种外形热防护层的高温隔热层与低温隔热层的厚度与材料热导率的不确定性对背温影响显著。