集装箱码头混合零空闲柔性流水作业调度优化

钟祾充，李文锋，贺利军，张 煜，周 勇

(武汉理工大学 交通与物流工程学院，湖北 武汉 430063)

0 引言

多式联运是全球货运重要的运输方式。当前，全球集装箱运输量骤增，亟需多式联运作业效率不断提高。集装箱码头是多式联运的重要枢纽，提高码头的作业效率是提高多式联运整体效率的关键所在。为集装箱任务合理分配设备和资源，从而获得高效的调度方案，具有重要的工程价值。

岸桥、集卡、场桥、泊位、堆场是集装箱码头作业的重要作业设备和资源。岸桥负责海侧集装箱的装卸，堆场为陆侧集装箱提供存储空间，场桥负责堆场作业，集卡负责集装箱运输。每个阶段的作业效率均对码头接卸转运总时间产生重要影响。

结合港口装卸作业特点，当前港口调度的研究可分为单阶段调度和多阶段调度。单阶段调度问题主要包括：港口泊位分配[1]、岸桥作业调度[2]、运输车辆调度[3]、堆场资源的配置与调度[4]等。多阶段调度问题同时考虑多个密切关联的作业环节，大部分是两阶段联合调度。比如，针对岸桥与集卡建立混合整数规划模型[5]，针对集卡与场桥建立二层规划模型[6]，针对泊位-堆场资源进行联合分配[7-8]，以及岸桥指派与泊位分配的集成调度[9-10]等。也有针对岸桥、集卡、场桥三阶段作业展开的联合调度优化研究[11-15]。其中，文献[15]将3个阶段的作业抽象为混合流水车间调度问题，但没有考虑集卡在场桥的空闲时间，也没有考虑岸桥的特殊作业性质。

在对港口调研时发现，岸桥在对船舶装卸作业时，时常出现空闲的情况。这使得港口的资源浪费巨大，增加了港口作业成本。为了充分利用昂贵成本的岸桥，港口对岸桥提出零空闲的需求。同时，随着港口不断向自动化、绿色化等方向发展，港口调度对低碳绿色、低成本等方面提出了更高要求。多目标优化成为港口调度的一大难题，针对港口多目标调度[11-12,15]等的研究文献正在快速增加。其中，文献[11]构建岸桥、集卡、场桥3种设备的调度优化模型，同时优化所有船舶的总出发延误时间和所有任务的总作业能耗。

求解港口调度问题的方法主要分为4类：精确算法、启发式算法、基于规则的启发式算法、仿真方法。KARAM等[12]设计了基于拉格朗日松弛的精确算法求解三阶段的联合调度问题。LIANG等[14]设计了一种基于规则的启发式算法求解泊位—岸桥联合调度问题。文献[15]针对低碳型集装箱码头连续泊位-岸桥分配问题，采用多目标高效非支配排序的遗传算法对其进行求解。文献[16]设计三阶段启发式算法求解三阶段联合调度问题。LIU[17]研究了一种迭代启发式算法求解混合整数规划模型，以最小化集装箱装卸的总成本，包括提速成本、延误成本、船舶罚款成本和操作成本。HE等[11]采用集成仿真优化的方法进行了研究。可以看出，相较于精确算法和仿真算法，启发式算法被更多地用于求解港口高度优化问题。文献中针对不同的港口问题，进行了针对性的算法设计。问题的变化和复杂性的增加将会影响算法编码解码的方式，也会影响算法的计算效率。

布谷鸟算法(Cuckoo Cearch, CS)是一种元启发式搜索，由YANG等[18]于2009年开发。CS具有较强的鲁棒性和通用性，为复杂的调度优化提供了新方法。该算法根据布谷鸟产卵行为提出3个假设并建立数学模型，引入昆虫的飞行轨迹莱维飞行机制，能够快速有效求解连续优化问题。然而，由于CS的连续搜索特性，CS在离散优化问题中应用有限。直到2014年，OUARAB等[19]首次提出使用CS解决旅行商问题。此后，越来越多的研究涉及离散CS求解旅行商、0-1背包等组合优化问题，但关于设计离散CS求解更复杂的多目标港口调度优化问题的研究仍较少。

综上所述，考虑港口的三阶段联合调度和零空闲岸桥作业约束，有助于从整体优化港口作业并降低成本。针对港口作业特征，借鉴车间调度领域的混合零空闲调度理论[20]，以总完工时间和总作业成本为优化目标，本文提出多目标集装箱码头三阶段混合零空闲柔性流水作业调度问题(three-stage Mixed No-idle Flexible Flow Scheduling Problem in Container Terminal, MNFFSP_CT)，并构建其数学模型。MNFFSP_CT是一个典型的NP难离散优化问题。考虑问题的多目标特性及离散特性，设计一种带间歇启动的多邻域局部搜索的改进离散布谷鸟(Improved Discrete Cuckoo Search, IDCS)算法，使得IDCS算法能够直接优化离散问题。最后，通过实验，验证模型的有效性和算法高效性。

1 问题描述

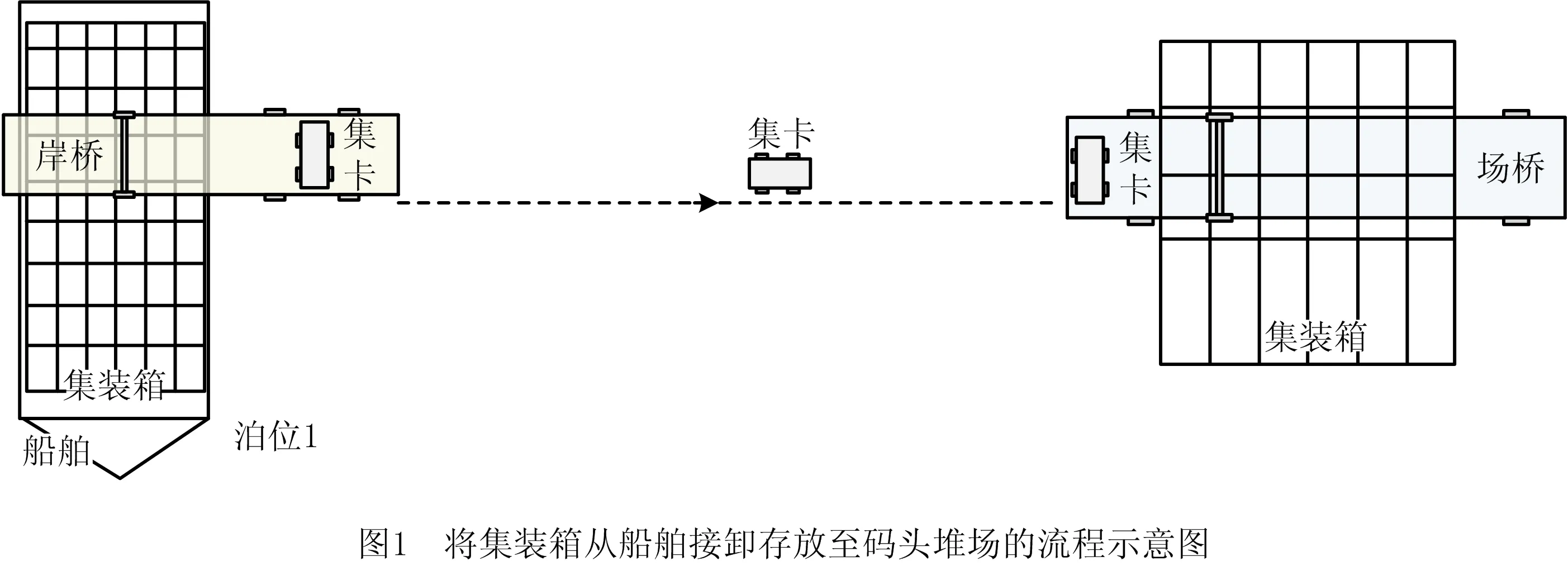
集装箱码头的作业包括装船和卸船两个过程，装船与卸船的作业过程相反。以集装箱卸船为例，描述港口作业过程(如图1)。假设有H个标准集装箱，需要从船舶转存到码头堆场。用O1工序表示岸桥作业阶段，O2工序表示集卡运输阶段，O3工序表示场桥作业阶段。如图2所示，每个集装箱h∈{1,2,…,H}都将依次经历O1→O2→O3三个工序，且均只经历一次。同工序的机器属于同构机，符合柔性流水车间调度问题的问题特征。但港口的三阶段作业仍有额外的实际作业约束，描述如下：

(1)考虑到实际港口的岸桥作业成本远高于集卡的作业成本，港口对岸桥提出零空闲作业时间的要求。

(2)接到转运任务的集卡到达岸桥位置，岸桥将集装箱装载到等候中的集卡。集卡将集装箱运输到符合集装箱储存需求的堆场。此时若没有空闲可提供作业的场桥，集卡则需要负载集装箱在堆场等待，直到有完成上一个任务的场桥出现。当集卡释放集装箱，并完成当前任务，若没接到下一项转运任务，则回到集卡池等候，若接到下一项转运任务，空载回到泊位等待岸桥装载集装箱。

(3)根据每个场桥的当前作业情况，为负载集卡分配场桥。

综上所述，传统的柔性流水车间调度问题无法准确地描述港口三阶段作业问题，其实际约束更加复杂。结合零空闲作业特征的岸桥，本文引入混合零等待柔性流水车间调度问题的基础模型，在此基础上进一步深刻描述问题，提出基于港口三阶段作业的混合零等待柔性流水车间调度问题(MNFFSP_CT)。

可将问题细分为以下几个子问题：①集装箱作业顺序调度问题；②集卡任务分配和开机数量的确定；③岸桥任务分配和开机数量的确定；④场桥任务分配和开机数量的确定。

模型假设如下：

(1)每台岸桥的大车移动能力一致，小车作业能力一致；

(2)每辆集卡的作业能力一致，所有集卡在所有岸桥和场桥间共享；

(3)每台场桥的大车移动能力一致，小车作业能力一致；

(4)不考虑集卡碰撞问题；

(5)集卡在集装箱码头单向行驶，从泊位b到堆场s的路径与从堆场s到泊位b的路径形成闭环路；

(6)泊位、堆场没有集装箱堆存缓冲区；

(7)船舶的集装箱转运任务具有优先级别，资源优先满足该任务需求；

(8)不考虑堆场翻箱倒箱导致的场桥工作时间；

(9)在作业期间，岸桥、集卡、场桥都是匀速作业，作业速度、功率给定；

(10)所有岸桥、集卡、场桥均是从零时刻开始。

2 数学模型

2.1 符号定义

j为集卡；h为需要卸载的集装箱；b为泊位；qb为岸桥；s为堆场；rs为场桥。

2.2 参数定义

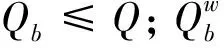
2.3 相关系数

θqb为岸桥qb在作业状态的成本系数；βqb为岸桥qb的开机成本；θj1为集卡j在负载作业状态的成本系数；θj0为集卡j在空载作业状态的成本系数；θj为集卡j在等待状态的成本系数；βj为集卡j的开机成本；θrs0为场桥rs在等待状态的成本系数；θrs1为场桥rs在作业状态的成本系数；βrs为场桥rs的开机成本。

2.4 变量

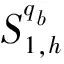
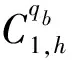
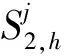
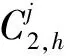
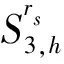
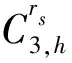
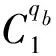
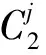
ITrs为场桥rs的总空闲时间；

ARh,j为集卡j负载集装箱h到达堆场的时刻；

ATh,j为集卡j负载集装箱h在堆场的等待时间；

RTh,j为集卡j在堆场释放集装箱h的时刻；

C1,max为当前集装箱岸桥阶段完工的最大完工时刻；

C2,max为当前集装箱集卡运输阶段完工的最大完工时刻；

C3,max为当前集装箱场桥阶段完工的最大完工时刻；

Cmax为Ω最大完工时刻；

TC为Ω全部完工的总成本。

2.5 目标函数

min(Cmax,TC)。

(1)

(2)

TC=TCQ+TCJ+TCR；

(3)

(4)

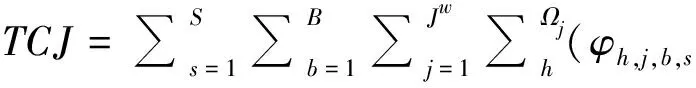
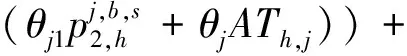
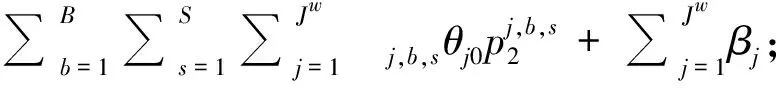
(5)

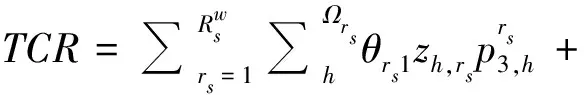
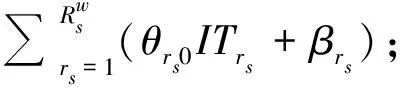
(6)

(7)

式(1)为目标函数集合，总完工时间Cmax和总作业成本TC；式(2)表示Ω最后一项任务的完工时间；式(3)表示Ω三个阶段的总作业成本；式(4)表示Ω在工序O1的作业成本；式(5)表示Ω在工序O2的作业成本；式(6)表示Ω在工序O3的作业成本；式(7)表示场桥rs完成Ωrs的工序O3所产生的空闲总时间。

2.6 约束

(8)

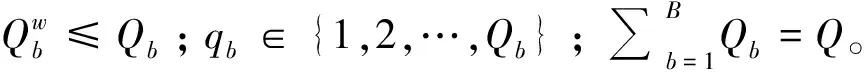
(9)

式中:Jw≤J；j∈{1,2,…,J}。

(10)

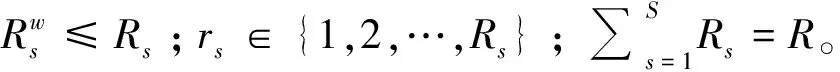
式(8)表示每个开机作业岸桥被分配的集装箱之和为任务集装箱总量；式(9)表示每个开机集卡被分配的集装箱数量之和为任务集装箱总量；式(10)表示每个开机作业场桥被分配的集装箱数量之和为任务集装箱总量。

(11)

(12)

(13)

(14)

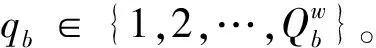
(15)

(16)

(17)

(18)

(19)

j∈{1,2,…,jw}。

(20)

式(15)要求集装箱必须完成岸桥作业之后才能进行集卡运输；式(16)表示工序O2包括以下三个部分：集卡负载集装箱从泊位到堆场，在堆场等待场桥作业，作业从堆场回到泊位；式(17)要求任意集装箱在集卡运输阶段仅被一辆集卡作业一次，不能被重复作业；式(18)要求集卡j在完成前一个集装箱转运任务之后，才可以重回泊位接受下一个集装箱的转运任务；式(19)要求下一个集装箱分配给最先完成前一个集装箱作业的集卡；式(20)要求场桥的作业开始时间必须在完成上一个任务之后且有集卡负载集装箱任务等待作业。

(21)

(22)

(23)

式(21)要求任意集装箱只被其中一台场桥作业一次；式(22)要求场桥rs在完成前一个集装箱作业任务之后，才可以进行下一个集装箱的作业任务；式(23)要求下一个集装箱分配给最先完成前一个集装箱作业的场桥。

3 问题求解方法

在MNFFSP_CT中，包括集装箱作业调度、岸桥分配、集卡分配、场桥分配4个子问题。需要考虑集装箱的排序，集装箱对应的集卡、岸桥、场桥，以及各类设备的开机数量。本文提出一种改进的布谷鸟算法求解MNFFSP_CT，算法包括以下4个部分：①针对集装箱的单链编码；②针对岸桥、集卡、场桥的三链解码，用于满足设备分配需求；③离散化的莱维飞行更新机制和个体抛弃机制，使算法直接应用于离散组合问题；④基于快速非支配排序策略(Fast Non-dominated sorting, FND)[22]的间歇启动多邻域局部搜索策略，可以平衡算法的全局和局部搜索能力，帮助算法跳出局部最优，同时减少计算资源的浪费。IDCS求解MNFFSP_CT流程图如图3所示。

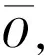
3.1 单链编码

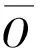
3.2 三链解码

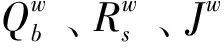
C1,max计算如下：

(24)

(25)

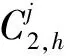
(26)

C3,max的计算如下：

(27)

(28)

ARh,j、ATh,j的计算如下：

(29)

(30)

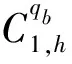
3.3 解的表达

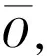
3.4 甘特图示例

表1 集装箱在3个作业阶段的作业时间

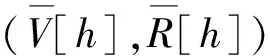
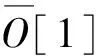
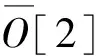
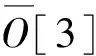
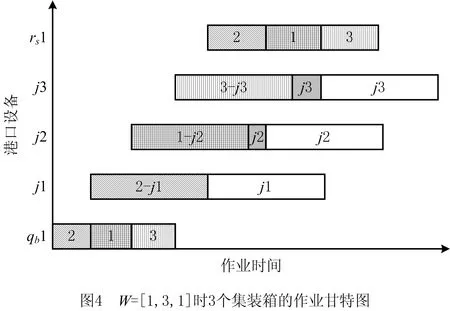
最终，根据编码解码规则，获得H=3,b=1,s=1,W=[1,3,1]的其中一种可行解：

其甘特图如图4所示。

3.5 改进离散布谷鸟算法(IDCS)

3.5.1 离散全局搜索

离散化的莱维飞行更新机制：

(31)

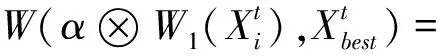
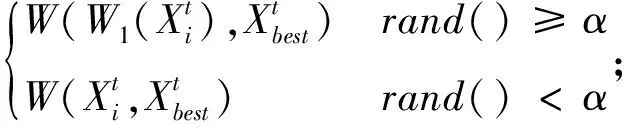
(32)

(33)

基于抛弃概率的离散更新机制：

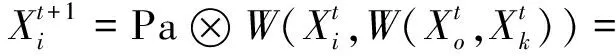
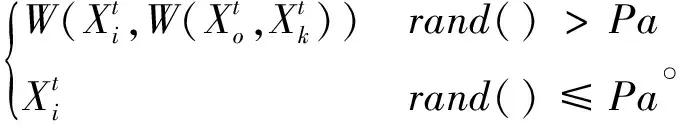
(34)

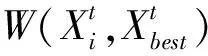
3.5.2 基于FND间歇启动的多邻域局部搜索

多邻域局部搜索是提高搜索精度的有效策略。为避免同一区域的较优个体消耗过多的计算资源，设计每完成50次迭代启动1次多邻域局部搜索。多邻域局部搜索如算法1所示，其搜索对象为当前种群FND分层后前N×β个个体，其中N=Popsize,β=0.3。该搜索策略基于3种邻域局部搜索设计：Swap局部搜索操作、Insert局部搜索操作、2-opt局部搜索操作。随机选择序列两个不同的位置p1

算法1多邻域局部搜索。

输入：非支配解X；

输出：更新后的解X。

1: %%%%扰动阶段

2: 设置 k=0

3: while k<3 do

4: 随机选取位置u和v, u≠v

5: π(X)=Insert(π(X),v,u); k=k+1

6: end while

7: %%%%探索阶段

8: 设置 k=0

9: while k<3 do

10: 随机选取位置u和v, u≠v, t=0

11: while t<20 do

12: if t=0 then

13: π(X)=Insert(π(X),v,u)

14: else if t=1 then

15: π(X)=swap(π(X),v,u)

16: else if t=2 then

17: π(X)=2-opt(π(X),v,u)

18: end if

19: ifX′Xthen

20:π(X′)π(X);k=k+1

21: else

22: t=t+1

23: end if

24: end while

25: end while

4 仿真实验分析

由于码头使用的设备数量取决于当前转运任务的集装箱数量，不同数量的任务需要通过实验获得设备最佳资源配置组合。实验的第一部分，为相同任务提供不同数量的设备，对比其优化结果，获得每种数量的最佳资源配置组合；第二部分实验基于最佳资源配置组合，进行多个算法对比，证明模型准确性和IDCS算法可行性高效性；第三部分实验根据某港口各阶段实际作业数据，通过IDCS算法求解80个集装箱数量的MNFFSP_CT，码头任务转运效率远高于80个集装箱/小时。所有算法和测试程序均用Delphi10.2编程实现。操作系统为Win10，处理器为Intel(R)Core(TM)i5-4210U 1.70 GHz，内存为4 GB。

第二部分实验基于以上7组不同集装箱数量的最佳资源组合，将IDCS算法与CS、改进的带精英策略的快速非支配排序遗传算法(Improved fast elitist Nondominated Sorting Genetic Algorithm, INSGA-II)[23]、蛙跳算法(Shuffled Frog-Leaping Algorithm, SFLA)[24]、人工蜂群算法(Artificial Bee Colony algorithm, ABC)[25]比较。

其中CS、INSGA-II、SFLA、ABC均采用与IDCS同样的编码解码方式，且CS使用最大顺序值(Largest-Order-Value, LOV)规则[26]将连续个体映射到离散个体。其中IDCS和CS的参数：种群大小Popsize、最大步长系数αmax、个体抛弃概率Pa。使用正交试验设计(Design of Orthogonal Experiment, DOE)[27]作为参数整定方法，选取中等规模问题(4,20,6)_80作为参数设置实验对象，将上述3个参数分为4个级别，参数选择量表为L16(43)的正交试验，每个参数组合下的测试问题分别进行20个独立运行试验，最终得到Popsize=20、αmax=0.8、Pa=0.1能够使算法的搜索能力稳定发挥。

以上每种算法对7组问题的求解都是独立运行30次，每种算法的每次独立运行时间均为50×Hms。

采用的分析指标是文献[28]中提出的多目标分析指标为R_NDS(Sr)，Sr指算法r所得Pareto解集，R_NDS(Sr)是算法r中未被支配的个体数占算法r中总的Pareto解集个体数的比率。

R_NDS(Sr)=1意味着Sr中所有的Pareto个体都不被支配，若R_NDS(Sr)=0.9意味着Sr中90%的Pareto个体都不被支配。本文中每个问题规模的数据结果可以在表2～表5中找到：表2是IDCS算法和CS算法的对比数据，表3是IDCS算法和INSGA-II算法的对比数据，表4是IDCS算法和ABC算法的对比数据，表5是IDCS算法和SFLA算法的对比数据。

表2 IDCS算法和CS算法的R_NDS对比数据

表3 IDCS算法和INSGA-II算法的R_NDS对比数据

表4 IDCS算法和ABC算法的R_NDS对比数据

表5 IDCS算法和SFLA算法的R_NDS对比数据

表2～表5加粗的数据说明该算法在该问题规模上所获得的不被支配的解多于另一个算法。例如表2～表4，在所有规模中IDCS都优于另一种算法。在表5中，只有(1,11,1)_10、(1,11,3)_40、(4,20,6)_80、(5,25,8)_120等问题规模中，IDCS略优于SFLA，而且另外3个规模下的结果差距不大，说明IDCS算法仅略优于SFLA算法，特别是在求解更高规模时，IDCS算法优势不明显，这为后面针对大规模的算例进行算法改进提供思路。总体而言，IDCS算法得到的解集更优，证明了IDCS算法求解多目标MNFFSP_CT的有效性。

第三部分实验基于某港口实际案例，为80个集装箱数量的接卸转运任务分配资源设备，并获得满足需求的优解。

某集装箱码头各阶段实际转运时间范围：岸桥作业时间范围为[100, 140]，场桥作业时间范围为[135, 175]，集卡从泊位到堆场的运输时间范围为[300, 333]，堆场到泊位的时间范围为[261, 300]。设置H=80的接卸转运任务，在时间范围内，采用随机生成的方式，获得每个设备对不同集装箱的作业时间。

显然，该集装箱港口的作业调度问题和资源分配问题符合多目标MNFFSP_CT问题模型。将IDCS算法用于求解80个集装箱的多目标MNFFSP_CT，获得满足min(Cmax,TC)且Cmax小于3 600 s的优化转运方案。其中Cmax为

集装箱作业顺序及每个集装箱所分配的岸桥、集卡、场桥如表6所示，数据形式为“集装箱编号(岸桥编号，集卡编号，场桥编号)”。

表6 80个集装箱的集装箱作业顺序及每个集装箱所分配的岸桥、集卡、场桥

这一结果表明多目标MNFFSP_CT问题符合集装箱码头实际作业需求，且IDCS算法可快速有效地求解实际问题多目标MNFFSP_CT问题，获得较优作业方案。

5 结束语

多式联运对集装箱码头的接卸转运效率提出了更高的要求。为满足岸桥零空闲作业需求，综合考虑码头各阶段作业，以最小化最大完工时间和作业成本为优化目标，提高接卸转运效率。研究内容及结论如下：

(1)针对岸桥零空闲作业需求，联合三阶段多并行作业特性，提出三阶段混合零空闲柔性流水作业调度模型(MNFFSP_CT)，并通过设计大中小7个规模集装箱转运问题，获得每个规模下最佳资源配置组合。通过实验验证了模型的准确性。

(2)基于MNFFSP_CT，设计包含4部分的改进离散布谷鸟(IDCS)算法，实现了对多目标MNFFSP_CT问题的有效求解。与CS、INSGA-II、SFLA、ABC多目标算法对比，验证了算法的高效性。但在更大规模上的求解，还需要进一步优化。

(3)通过 IDCS求解80个集装箱的MNFFSP_CT，可获得高于80个集装箱/小时的转运速率，总完工时间小于 3 600 s。对实际集装箱码头有实际的工程意义。

本文从整体角度对港口进行联合调度优化，松弛每个作业阶段的作业约束，例如岸桥作业部分岸桥的多机协同防冲突调度问题、堆场部分可能存在的翻箱倒箱问题等。在未来的研究中，同时考虑港口的三阶段混合零空闲柔性流水作业调度问题与各阶段的约束，既可以满足集装箱的调度优化，也可以满足各个阶段设备的问题特征，使求解方案更加接近实际需求。