多目标变分批混合流水车间调度算法自动设计

张 彪，孟磊磊，桑红燕，卢 超

(1.聊城大学 计算机学院，山东 聊城 252000；2.中国地质大学(武汉)计算机学院，湖北 武汉 430074)

0 引言

混合流水车间调度问题(Hybrid Flowshop Scheduling Problem, HFSP)作为流水车间调度问题的一个分支，因其重要的理论价值和实用价值引起了研究人员的广泛关注[1-5]。HFSP常见于电子、家具、纺织、石化、制药等各种柔性制造车间中[6-7]。HFSP要根据生产约束确定各阶段的作业顺序和机器分配，即使是在非常小规模的问题实例上，也被证明是NP困难的[1]。在目前大多数关于HFSP的研究中，作业是不能被分割的，即每个作业在某一特定阶段完成之前不能转移到下游阶段。然而，在许多现实场景中，这将对生产效率产生负面影响，在这些场景中，一个作业是由一系列相同的加工单元组成的。

REITER[8]首先在作业车间调度问题中引入了批量流技术，高效地完成了基于生产效率的调度目标。如今，批量流技术被制造企业广泛使用，以提升它们的客户服务[9]。批量流技术将一个给定的批次分割成若干较小的子批，以实现在一个多阶段制造车间中同一批次在不同阶段中的并行加工。也就是说，批次的一个子批一旦在某一阶段完成加工，就可以立即运输到下游阶段。因此，它的好处是减少生产周期，从而更快地生产和交付产品。此外，它还具有减少在制品库存、线边仓和空间需求的优点。批量流的划分方法可分为等量分批、一致分批和可变分批[9-10]。在等量分批下，同一批次的不同子批规模是相同的，并且在不同阶段保持一致；在一致分批下，批次的不同子批规模可能不同，但在不同阶段保持一致；而在可变分批下，批次的不同子批规模可能不同，并且在不同阶段也保持变化。显然，可变分批是最复杂的情形，等量分批和一致分批则可作为可变分批的特例。

因此，本文将可变分批引入HFSP中，除了考虑批次顺序和机器分配之外，每个批次的批次分割(即子批数量和子批规模)都应被考虑。本文研究的问题比经典HFSP要困难得多，显然也是NP困难的。批量流技术能够缩短生产周期，但它也有实现成本，如子批的运输和管理。也就是说，子批的数量越大，最大完工时间就可能越小，但相应的运输成本会增加。因此，考虑到实际中子批的运输成本，子批的总量会受到限制。总而言之，最大完工时间与子批总量之间通常存在着一种权衡关系。因此，本文将致力于解决多目标变分批混合流水车间调度问题(Multi-objective Hybrid Flowshop Scheduling Problem with Variable Sublot, MOHFSP_VS)，同时优化最大完工时间和子批总量。

在现有批量流HFSP文献中，涉及到多目标优化，只查到两篇论文。CHEN等[11]研究了一种具有一致分批的HFSP，同时考虑机器具有不同的加工速度，以最小化最大完工时间和能耗为目标，其提出一种多目标遗传算法，在其研究中，每个批次的子批数量是预先确定的。LI等[12]研究了一种可变子批的多目标HFSP，最小化4个目标，即逗留时间惩罚、能量消耗、提前和延迟值。需要注意的是，在该研究中，可变子批只是指每个批次在不同阶段的子批数量可能不同，但同一批次不同子批的规模是相同的，即每个子批的加工时间是预先确定的。为求解上述问题，LI等[12]提出了基于分解的多目标进化算法。在上述研究中，来自不同批次的子批可以混合。但当不同批次间具有启动作业时，这种设置是不现实的，因为要频繁地进行切换，严重影响加工效率。因此，本文设定来自不同批次的子批不可以混合。此外，上述研究均将批量流作为问题约束，没有研究生产效率与批量分割之间的权衡关系，而本文将重点研究这一问题。ZHANG等[13]研究了基于一致分批的HFSP，同时考虑了启动和运输操作，并利用AAD算法取得了满意的效果。本文将在此基础上，研究基于可变分批的HFSP，利用自动算法设计(Automated Algorithm Design,AAD)方法自动构建MOEA。

因为问题的NP难特性，为解决MOHFSP_VS，本文采用多目标进化算法(Multi-objective Evolutionary Algorithm, MOEA)进行求解。众所周知，MOEA的性能在很大程度上依赖于算法参数值(包括数值参数和类别参数)的设置[14-15]。事实上，这些参数的设置取决于所解决的问题。然而，传统的设置过程可能会受到以往经验的影响。为了消除这些限制，本文引入一种自动算法设计(AAD)方法[16-19]基于算法框架来自动构建MOEA。本文采用的AAD方法称为I/F-Race(iterated F-race)[16]，它通过测试一组测试算例，自动寻找并组合最佳参数取值，从而构建一个针对给定问题表现优异的自动算法，避免了过多的人为干预。关于所选择的算法框架，本文采用多目标离散人工蜂群算法(Multi-objective Discrete Artificial Bee Colony algorithm, MDABC)[20]。MDABC利用分解策略，通过使用聚合函数将多目标问题分解为若干标量子问题，并通过协作的方法同时优化这些子问题。选择该算法框架的原因如下：一方面，MDABC在HFSP上表现出了优异的性能；另一方面，求解MOHFSP_VS，需要同时解决一些耦合的问题，如批次排序、机器分配和批量分割，因此，在解的编码中需要包含不同的部分来呈现不同的解空间信息，每个部分都有其特定的邻域结构。此外，由于问题间是高度耦合的，使用基于邻域结构的元启发式算法可以实现不同邻域结构之间的交互。而MDABC正是基于变邻域下降策略(Variable Neighborhood Descent, VND)开发的一种基于协作的MOEA。

本文的主要贡献总结如下：①在可变分批策略下，研究了考虑启动和运输操作的多目标HFSP；②建立了多目标混合整数规划模型，同时优化最大完工时间和子批总数；③引入了一种自动算法设计方法，构建高性能的MOEA。

1 问题描述

在MOHFSP_VS中，一系列批次要经过连续的阶段进行加工，每个阶段包含若干相同的机器，并且每个批次包含若干加工单元，加工单元的数量称为批次规模。在变分批策略下，每个批次被分割成若干子批，受运输管理的限制，子批的数量有一个最大限定值。每个子批包含不同数量的加工单元，加工单元的数量称为子批规模。批次的子批数量和子批规模在不同阶段是发生变化的。来自同一批次的不同子批需要在每个阶段的同一台机器上连续加工，子批内的加工单元也是连续性地加工。也就是说，一个子批的加工时间是子批规模和单位加工时间(一个加工单元的加工时间)的乘积。不同的批次之间机器需要执行启动操作，而同一批次的任意两个连续子批间则不需要启动操作。此外，不同批次在不同阶段需要的启动时间也不同的。当一个子批在某一阶段完成加工后，立即被运输到下一阶段，两个不同连续阶段之间的运输时间是不同。MOHFSP_VS的特征如下:

(1)所有批次中的加工单元在0时刻均是可用的，不考虑优先权和中断。

(2)机器可以有空闲时间，各阶段之间的缓冲区容量是无限的。

(3)每个批次都要经过所有阶段，在一个阶段上，每个批次只能分配到一台机器。

(4)每个批次被分割成若干子批，但子批数有一个限定的最大值。每个子批规模可能不同，相同子批在不同阶段上的规模也可能不同。

(5)每个子批在某一阶段完成加工后，将立即传输到下游阶段。

(6)同一批次的各个子批在一台机器上连续地进行加工。在运输到特定阶段后，第一个子批可在启动操作之后开始加工，其余的子批在运输到这个阶段后，在前一个子批完成加工后开始加工。

(7)在任意时刻，一台机器至多只能加工一个加工单元，一个子批中的加工单元连续地进行加工。

1.1 数学模型

MOHFSP_VS需要确定不同阶段的批次分割、批次顺序和机器分配。为了建立多目标混合整数规划模型，表1和表2所示为问题参数和决策变量的符号与定义。对于可变分批，与等量和一致分批相比，存在一个重要的约束条件，即对于一个给定的批次，它的任一子批都不能包含属于那些在先前阶段未完成并转移到该阶段的子批中的加工单元。因此，该模型的主要贡献在于引入了一个决策变量Xi,j,e,e′，用来描述批次的子批规模间关系。

表1 模型问题参数符号与定义

表2 模型决策变量符号与定义

基于表1和表2中的符号表示，本文建立的多目标混合整数规划模型如下：

目标函数：

minMS;

(1)

(2)

s.t.

MS≥Em,j,L,∀j∈J;

(3)

Si,j,e≥0,∀i∈I,j∈J,e∈[1,L];

(4)

(5)

(6)

B1,j,1≥t1,j,∀j∈J；

(7)

Ei,j,e-Bi,j,e=pk,j×Si,j,e，

∀i∈I,j∈J,e∈[1,…,L]；

(8)

Bi,j,e+1-Ei,j,e≥0，∀i∈I,

j∈J,e∈[1,…,L-1]；

(9)

Yi,j,j′,k+Yi,j′,j,k≤1，∀j,j′∈J,k∈Mi；

(10)

Yi,j,j′,k+Yi,j′,j,k≤Di,j,k+Di,j′,k，

∀i∈I,j,j′∈J,k∈Mi；

(11)

Di,j,k+Di,j′,k-1≤Yi,j,j′,k+Yi,j′,j,k,

∀i∈I,j,j′∈J,k∈Mi；

(12)

Bi,j,1-Ei,j′,L-ti,j+Q×(3-Yi,j′,j,k-Di,j,k-

Di,j′,k)≥0，∀i∈I,j,j′∈J,k∈Mi；

(13)

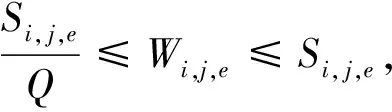
∀i∈I,j∈J,e∈[1,…,l]；

(14)

Bi+1,j,1≥Ei,j,1+fi,j×Wi,j,1+si+1,j,

∀i∈{1,2,…m-1},j∈J;

(15)

Bi+1,j,1+Q×(1-Xi+1.j,1,e′)≥fi,j×Wi,j,e′+ti+1,j+

Ei,j,e′,∀i∈I,j∈J,e′∈[1,…,L];

(16)

Bi+1,j,e+Q×(1-Xi+1,j,e,e′)≥Ei.j,e′+fi,j×Wi,j,e,

∀i∈I,j∈J,e,e′∈[2,…,L];

(17)

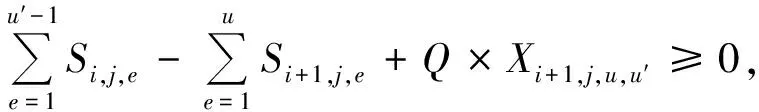
i∈[1,…,m-1],j∈J,

u∈[1,…,L],u′∈[2,…,L];

(18)

Wi,j,e≥Wi,j,e+1,∀i∈I,j∈J,e∈[1,…,L-1];

(19)

Di,j,k∈{0,1},

∀i∈I,j∈J,k∈M,k∈{1,2,…,σi};

(20)

Yi,j,j′,k∈{0,1},∀i∈I,j,j′∈J,k∈M;

(21)

Wi,j,e∈{0,1},∀i∈I,j∈J,e∈[1,…,L];

(22)

Xi,j,e,e′∈{0,1},∀i∈I,j∈J,e,e′∈[1,…,n]。

(23)

其中：式(1)定义了模型的目标之一：最大完工时间(MS)。式(2)定义了模型的目标之二：批次在所有阶段的子批总数(NOS)。式(3)保证MS要大于每个批次的最后一个子批在最后一阶段上的完工时间。式(4)要求在每个阶段每个子批的规模要大于等于0。式(5)要求在每一阶段对于给定的批次，子批规模之和等于批次的总规模。式(6)保证了每个批次都要经过所有阶段的加工，并且在每个阶段只能分配到一台机器上。因为在问题中考虑了启动操作，式(7)要求在第一个阶段，每个批次的第一个子批的开始加工时间要大于它的启动时间。式(8)保证了每个子批的加工不能被打断。式(9)保证在每个阶段，来自给定批次的子批只有在它相邻的前一个子批完成加工之后才能开始加工。式(10)～式(12)共同定义了变量Di,j,k和Yi,j,j′,k的关系，两个变量的取值决定了批次的机器分配和调度次序。式(13)表达了如果有任意的批次在其之前加工，每个批次的第一个子批只有在启动操作完成之后才能开始加工。式(14)定义了决策变量Si,j,e和Wi,j,e的关系，当Si,j,e>0时，Wi,j,e=1，而当Si,j,e=0时，Wi,j,e=0。式(15)表达了在非第一阶段的各个阶段，每个批次的第一个子批只有在先前阶段完成加工并到达后才能开始加工。式(16)定义了在非第一阶段的各个阶段，每个批次的第一个子批只有在相关的另一子批在前一阶段完成加工并到达以及完成启动操作后才能开始加工。式(17)表述了每个批次的子批(第一子批除外)是否能够在相关子批的前一阶段完成加工并到达后开始加工。式(18)表明对于给定的批次，对于其内的子批，不能包含属于在前一阶段还没有完成加工的子批内的加工单元。式(16)～式(18)共同定义了应用变分批之后的重要约束：对于一个给定的批次，其任一子批都不能包含在先前阶段未完成或者没有转移到该阶段子批中的加工单元。式(19)保证了优先给予位列前面的子批去容纳加工单元。式(20)～式(23)定义了4个决策变量的取值范围。

1.2 两目标的权衡关系

变分批技术能够有效降低最大完工时间，但其自身也有实现成本：分批之后，子批总数增加，需要管理更多的运输作业，从而加大了运输成本。同时，不充分的分批会限制提升生产效率的效果，从而导致较大的最大完工时间。也就是说，最大完工时间和子批总数存在着权衡关系。为了进一步解释和评估它们之间的关系，这里考虑一个具有4个批次和2个阶段(第一阶段拥有3台机器，第二阶段拥有2台机器)的测试实例。每个批次的最大子批数量设为5，其他相关的加工数据如下：

fi,j=[12,10,10,11]，Tj=[66,57,79,85]。

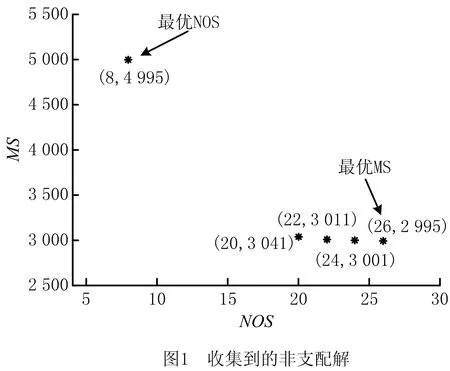
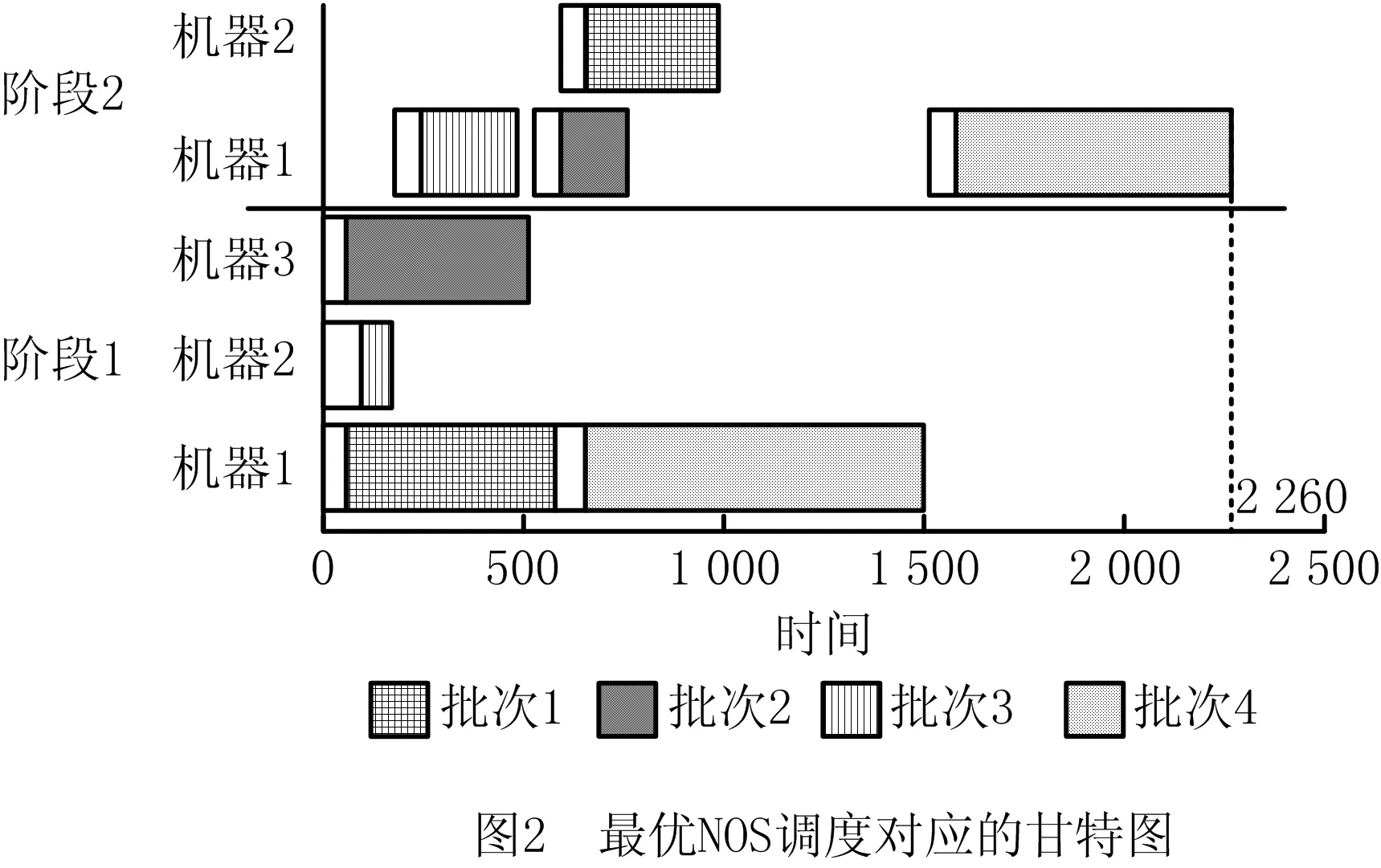
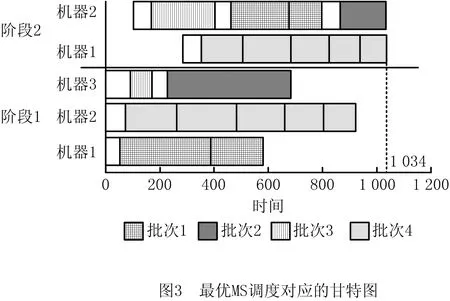
事实上，一个多目标优化问题(Multi-objective Optimization Problem, MOP)的Pareto最优解能够成为MOP标量子问题的最优解[13]。因此，为了得到MOHFSP_VS的Pareto最优解，利用50个均匀分布的权重向量对两个目标进行线性加权，生成50个不同的标量子问题。采用IBM ILOG CPLEX12.7.1(著名的商用数学规划模型求解器)求解50个标量子问题的最优解，并将收集到的非支配解标注到图1中。从图1中可以看出，MS和NOS两个目标不能同时被优化，即随着子批总数的增加，最大完工时间在逐渐减少。此外，图1中最优MS和最优NOS两个解所对应的调度方案如图2和图3所示。图2为最优NOS对应的调度甘特图，从图中可以看出每个批次均只含有一个子批，NOS也就最小，MS相应地也就最大，此调度方案相当于不采用分批的HFSP调度。图3为最优MS对应的调度甘特图，从图中可以看出每个批次均分割为若干子批，NOS最大，MS相应地也就最小。综上所述，变分批技术能够有效地降低MS，同时，MS和NOS两目标间存在着权衡关系。

2 针对问题特性的算法配置及自动算法设计

MDABC主要包含种群初始化阶段、基于VND的雇佣蜂阶段、基于协作的旁观者蜂阶段以及基于解交换的侦查蜂阶段4个阶段[19]。在种群初始化阶段，由于采用了分解策略，需要在解空间中随机生成N个解(Xi,i=1,…,N)，每个解都要分配一个特定的权重(Wi,i=1,…,N)；在基于VND的雇佣蜂阶段，每个解通过VND策略搜索邻域结构来改进自己；在基于协作的旁观者峰阶段，它的核心思想在于利用优良解探索更多的协作信息；在基于解交换的侦查蜂阶段，会判定每个子问题的解是否在过去的L次连续迭代中得到了改进。如果没有，则寻找它所支配的邻近子问题中的一个解，然后，两个邻近子问题交换它们的解。

在MDABC中，存在3个需要配置的数值参数，包括子问题的数量(N)、每个子问题邻近子问题的数量(T)、交换解前连续不成功的代数(L)。对于可配置的类别参数，它们与MOHFSP_VS的问题特征紧密相关。接下来，考虑到问题特性，本文先设计了问题的编码方案和权重的产生方法，然后详细介绍了4个可配置的类别参数和1个相关的数值参数。

2.1 问题编码与权重产生

根据问题描述，求解MOHFSP_VS需要同时解决3个相互耦合的问题，即批次排序、机器分配以及批次分割。利用元启发式算法求解优化问题时，解的编码需要承载必要的信息，能够利用解码规则翻译成详细的调度方案。在有限的计算成本限制下，批次序列编码[21-23]在研究中得到了广泛应用且表现优异。批次序列表示在第一阶段的批次调度顺序，而在后续阶段中，批次的调度顺序由相应的启发式规则得到，机器分配同样如此。由于不允许来自不同批次的子批混合在一起，批次分割需要单独处理。综上所述，在本文中，解的编码分为两部分：①一个n维的向量π={π1,…,πj,…,πn}，其中πj表示批次索引，n表示批次的数量；②批次分割矩阵的集合，即Δn={ψ1,…,ψj,…,ψn}，其中ψj为具有m行L列的批次分割矩阵,

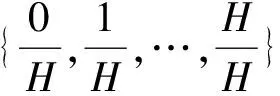
2.2 动态解码和可配置的解码启发式规则

解码过程是将解的编码翻译成可行调度方案的过程。为了求解MOHFSP_VS，需要同时考虑3个问题：批次序列，机器分配，以及批次分割。鉴于变分批技术的引入，为防止不可行解的产生，本文提出一种动态的解码过程，如下所示：

步骤1在第一个阶段，即i=1,依次从序列π={π1,…,πj,…,πn}中取出πj。执行以下流程：

步骤 1.1根据可配置的启发式规则，确定πj的分配机器和机器空闲时间。

步骤 1.2计算批次πj的各子批在第一阶段的加工时间。根据加工约束，依次调度各子批。有如下两种情形：

(1)若为第一子批，则子批的开始加工时间为机器的空闲时间和启动时间之和。完工时间为开始加工时间和子批的加工时间之和。利用完工时间更新机器的空闲时间。

(2)若不是第一子批，则子批的开始加工时间为机器的空闲时间。完工时间为开始加工时间和子批的加工时间之和。

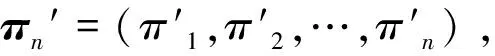
步骤 2.1根据可配置的启发式规则，确定πj′的分配机器和机器空闲时间。

步骤 2.2计算πj′的各子批在阶段i的加工时间。定义4个临时变量：变量ScheduledUnits记录已调度过的加工单元数量、SchedulingUnits记录可以调度的加工单元数量、ArrivedUnits记录已到达的加工单元总数、ArrivedSublot记录还没到的最邻近子批。根据加工约束，依次调度各子批。有如下两种情形:

(1)若为第一子批，执行如下流程：

步骤 2.2.1在调度时刻点，即机器的空闲时间和启动时间之和，得到ArrivedUnits的值。具体方法如下：依次从ArrivedSublot遍历到Tj，直到某一子批在调度时刻点还未达到阶段i，利用这一子批更新ArrivedSublot。将在调度时刻点已经达到阶段i的子批所包含的加工单元数记录到ArrivedUnits中。

步骤 2.2.2得到SchedulingUnits的值，具体方法为SchedulingUnits=ArrivedUnits-ScheduledUnits。开始调度第1子批，有如下两种情形:

1)若第一子批在阶段i所包含的加工单元数小于或等于SchedulingUnits，则在调度时刻点开始进行加工，开始加工时间即为调度时刻点，完工时间为开始时间与加工时间之和。利用完工时间更新机器的空闲时间，利用该子批所包含的加工单元数更新SchedulingUnits和ScheduledUnits。

2)若第一子批在阶段i所包含的加工单元数大于SchedulingUnits，则需要等待足够的加工单元数到来之后才能开始进行加工。具体方法如下：依次从ArrivedSublot遍历到Tj，将子批的加工单元数加到ArrivedUnits，得到SchedulingUnits，该遍历到SchedulingUnits大于等于第一子批在阶段i所包含的加工单元数停止，并更新ArrivedSublot。第一子批开始加工，开始时间为子批ArrivedSublot-1运输到阶段i的时间，完工时间为开始时间与加工时间之和。利用完工时间更新机器的空闲时间，利用该子批所包含的加工单元数更新SchedulingUnits和ScheduledUnits。

(2)若不是第一子批，执行如下流程：

步骤2.2.1在调度时刻点，即机器的空闲时间，得到ArrivedUnits的值。具体方法如下：依次从ArrivedSublot遍历到Tj，直到某一子批在调度时刻点还未达到阶段i，利用这一子批更新ArrivedSublot。将在调度时刻点，已经达到阶段i的子批所包含的加工单元数记录到ArrivedUnits中。

步骤 2.2.2得到SchedulingUnits的值，具体方法为SchedulingUnits=ArrivedUnits-ScheduledUnits。开始调度当前子批，有如下两种情形:

1)如果当前子批在阶段i所包含的加工单元数小于或等于SchedulingUnits，则在调度时刻点开始进行加工，开始时间即为调度时刻点，完工时间为开始时间与加工时间之和。利用完工时间更新机器的空闲时间，利用该子批所包含的加工单元数更新SchedulingUnits和ScheduledUnits。

2)如果当前子批在阶段i所包含的加工单元数大于SchedulingUnits，则需要等待足够的加工单元数到来之后才能开始进行加工。具体方法如下：依次从ArrivedSublot遍历到Tj，将子批的加工单元数加到ArrivedUnits，得到SchedulingUnits，该遍历到SchedulingUnits大于等于当前子批在阶段i所包含的加工单元数停止，并更新ArrivedSublot。当前子批开始加工，开始时间为子批ArrivedSublot-1运输到阶段i的时间，完工时间为开始加时间与加工时间之和。利用完工时间更新机器的空闲时间，利用该子批所包含的加工单元数更新SchedulingUnits和ScheduledUnits。

可配置的启发式规则描述如下。考虑批次序列，本文引入了“先到先得”规则，因为其在求解以时间为目标的调度问题[1]时表现出了良好的性能。具体来说，在第一阶段，编码中的批次序列可以直接反映批次的调度顺序。而在后续阶段的批次调度顺序均按“先到先得”规则而定，即在上一阶段较早完成的批次，可优先在下一阶段进行加工。考虑到批次分割的特点，本文提出两种方法来实现“先到先得”规则：①“子批优先”(Sublot Preemption, SP)，即在前一阶段较早完成的子批所属的批次具有优先加工权;②“批次优先”(Lot Preemption, LP)，即在前一阶段较早完成的最后一个子批所属的批次具有优先加工权。考虑机器分配，本文采用“优先可用”(First Available, FA)和“优先完成”(First Completion, FC)两种规则。“优先可用”表示具有较早可用时间的机器拥有优先分配权；“优先完成”表示较早能够加工完批次的机器拥有优先分配权。

综上所述，针对问题的解码过程，可得到4个可配置的解码启发式规则组合，即“批次优先”和“优先可用”的组合(LP_FA)、“批次优先”和“优先完成”的组合(LP_FC)、“子批优先”和“优先可用”的组合(SP_FA)以及“子批优先”和“优先完成”的组合(SP_FC)。

2.3 可配置的初始解生成方法

好的初始解生成方法有利于提高元启发式算法搜索效率。本节基于问题编码，设计了初始解的生成方法。首先，介绍了分割矩阵Δn的生成方法，然后给出了批次序列π的生成方法。对于初始化Δn，设计了3种方法，即均匀初始化(Uniform Initialization，UI)、随机初始化(Random Initialization，RI)和混合初始化(Mixed Initialization，MI)。具体流程描述如下：

(1)均匀初始化方法

(2)随机初始化方法

步骤 1对于每个批次j(j=1,…,n)来说，首先将剩余规模rj的值设为Tj。对于批次j来说，在阶段i(i=1,…,m)上，依次从子批e=1到子批e=L，确定它们的子批规模。

步骤 2若e∈[1,L-1]，批次j的子批e在阶段i上的子批规模Si,j,e在区间[0,rj]内随机产生。

步骤 3若e=L，批次j的子批e在阶段i上的子批规模Si,j,e设置为rj。

(3)混合初始化方法

步骤 1以一种均匀的方式分割批次j(j=1,…,n)。

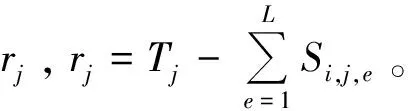
步骤 2.1在区间[0,Si,j,e]得到一个随机整数Random，然后以50%的概率执行Si,j,e=Si,j,e+Random或者Si,j,e=Si,j,e-Random。

步骤 2.2对于子批L+1-e，则以50%的概率执行Si,j,L+1-e=Si,j,L+1-e-Random或者Si,j,L+1-e=Si,j,L+1-e+Random。

步骤 2.3打乱子批排序。通过上述步骤，每个子批规模已被确定。为保证随机性，子批序列被随机打乱。

一旦分割矩阵Δn生成，各批次中子批的加工时间就能够确认，因此根据一些启发式规则，批次序列πn的初始化也能够完成。本文引入了文献中用于初始化批次排列的6种启发式规则，它们均在求解HFSP中表现出了较好的性能，分别为SPT(shortest processing time)，VSPT(variant of SPT)，NEH(Nawaz, Enscore, and Ham)，GRASP(greedy randomized adaptive search procedure)，GRASP_NEH，以及RI(random initialization)。除了RI之外，因为批量流的应用，这些规则都不能直接用于MOHFSP_VS，具体操作见文献[13]。

综上所述，本文采用了3种批次分割矩阵初始化方法和6种批次序列初始化方法。将它们结合起来，总共可以得到18种方法来进行解的初始化。

2.4 可配置的分解策略和目标归一化

基于分解策略求解组合优化问题，有两种通用的策略去聚集多个目标：加权和方法(Weighted Sum)和切比雪夫方法(Tchebycheff)[24]。本文将这两种分解方法设置为可配置的。此外，在先期实验中，已知两个目标有不同的量纲。若不采取措施将导致算法偏向于量纲大的目标进行搜索。为解决这一问题，本文采用简单的Max-Min方法对两个目标进行归一化，如式(24)所示。归一化方法的使用和不使用在本文中被认为是可配置的。

(24)

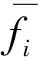
根据上述定义，两目标的上下界可以经过下列公式得出：

(25)

(26)

(27)

(28)

2.5 邻域结构设计及可配置的协同操作

MDABC算法在雇佣蜂阶段，采用了VND策略。因此，需要根据解的编码来设计邻域结构。对于批次序列向量π={π1,…,πj,…,πn}，本文采用两种应用广泛的邻域结构，即插入和交换策略。对于批次分割矩阵集合Δn={ψ1,…,ψj,…,ψn}，本文提出一种批次分割矩阵ψj的变化操作。在此基础上，提出两种组合结构，分别组合插入操作和变化操作，以及交换操作和变化操作。5种邻域结构具体如图4所示：①插入操作：从批次序列向量πn中随机选择一批次，然后将它随机插入到一个随机选择的位置中。②交换操作：从批次序列向量πn中随机选择两批次，然后交换它们的位置。③变化操作：从批次分割矩阵集合中随机选取带有至少两个子批的批次ψj。针对ψj，在每一阶段i，随机选择两个子批，将一个子批的规模缩减一个基于分布U[0,5]得到的一整数，而相应地，将另一子批的规模增加一个相同的整数。④组合结构1：先执行插入操作，再执行变化操作。⑤组合结构2：先执行交换操作，再执行变化操作。

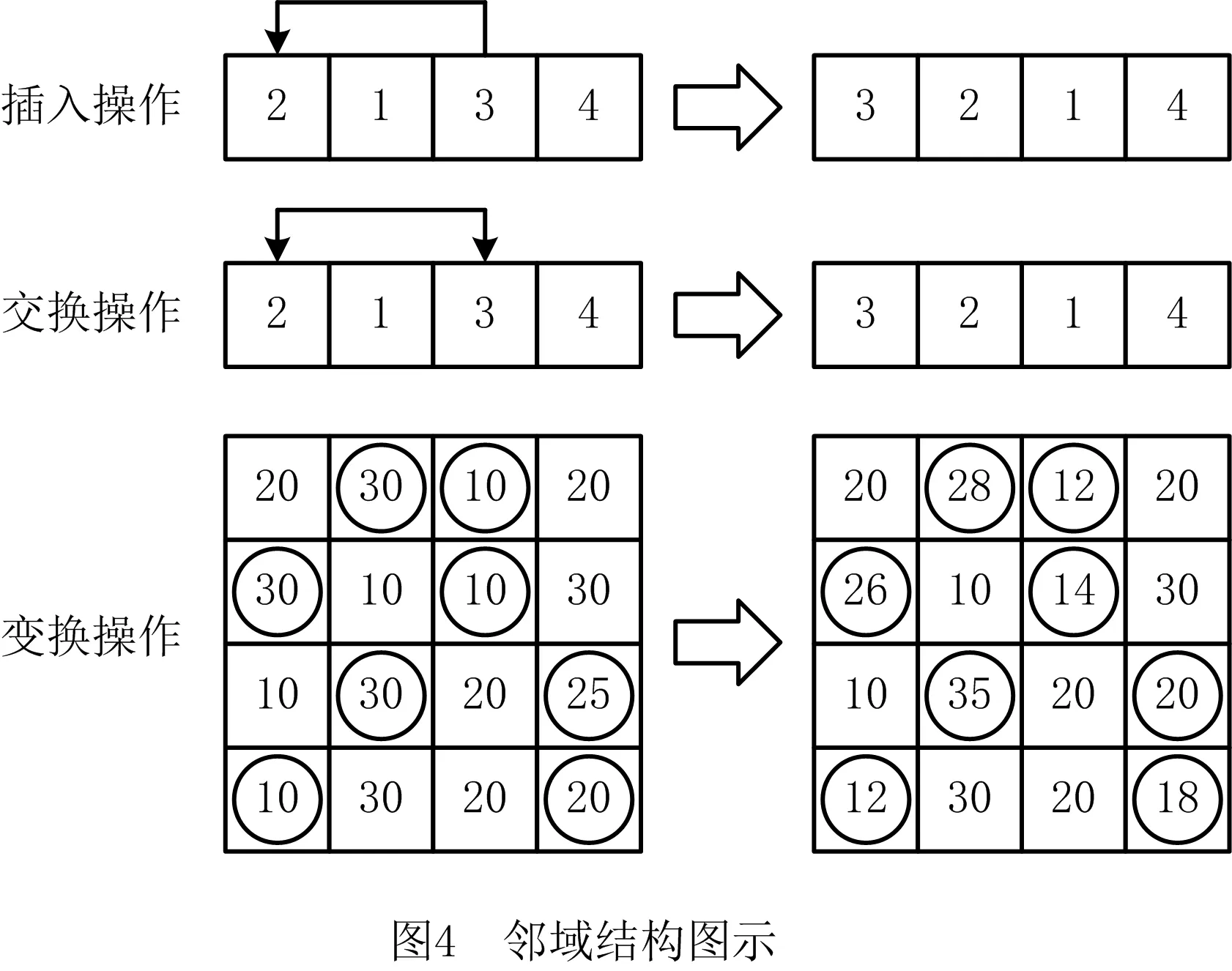
在MDABC算法的第二阶段，两个解之间需要执行协同操作。对于车间调度问题，交叉算子具有良好的性能，能够在保证遗传优良信息的基础上，同时又有一定的全局搜索性。对于组合优化问题，应用广泛的交叉算子有部分映射交叉(Partial Mapped Crossover，PMX)、顺序交叉(Order Crossover，OX)、基于位置交叉(Position-based Crossover，PBX)、基于顺序交叉(Order-Based Crossover，OBX)、循环交叉(Cycle Crossover，CX)和子环交换交叉(Subtour Exchange Crossover，SEX)。针对解编码中的批次序列向量，图5展示了上述交叉算子的示意图。而对于批次分割矩阵，由于受固定批量大小的约束，上述交叉算子可能会产生不可行解。因此，为了能够实现信息共享，促进它们之间的协作，本文引入了矩阵选取操作[13]，如图6所示。具体来说，当确定一个批次在分割信息时，其在每一阶段的批次分割，以一定的概率从两个父解中的批次分割矩阵中选取(以下称为选取概率)。从批次1到批次n，依次采取上述操作，确定完整的批次分割信息。

2.6 自动算法配置问题

本节给出自动算法配置问题，其形式化定义由BIRATTARI[16]给出。在配置问题中，存在4个可配置的数值参数和4个可配置的类别参数。数值参数包括交换解前连续不成功的代数、每个子问题邻近子问题的数量、子问题的数量，以及选取概率。分类参数包括初始化方法、解码策略、聚集方法，以及批次序列的交互方法。表3列出了可配置参数及其分布。

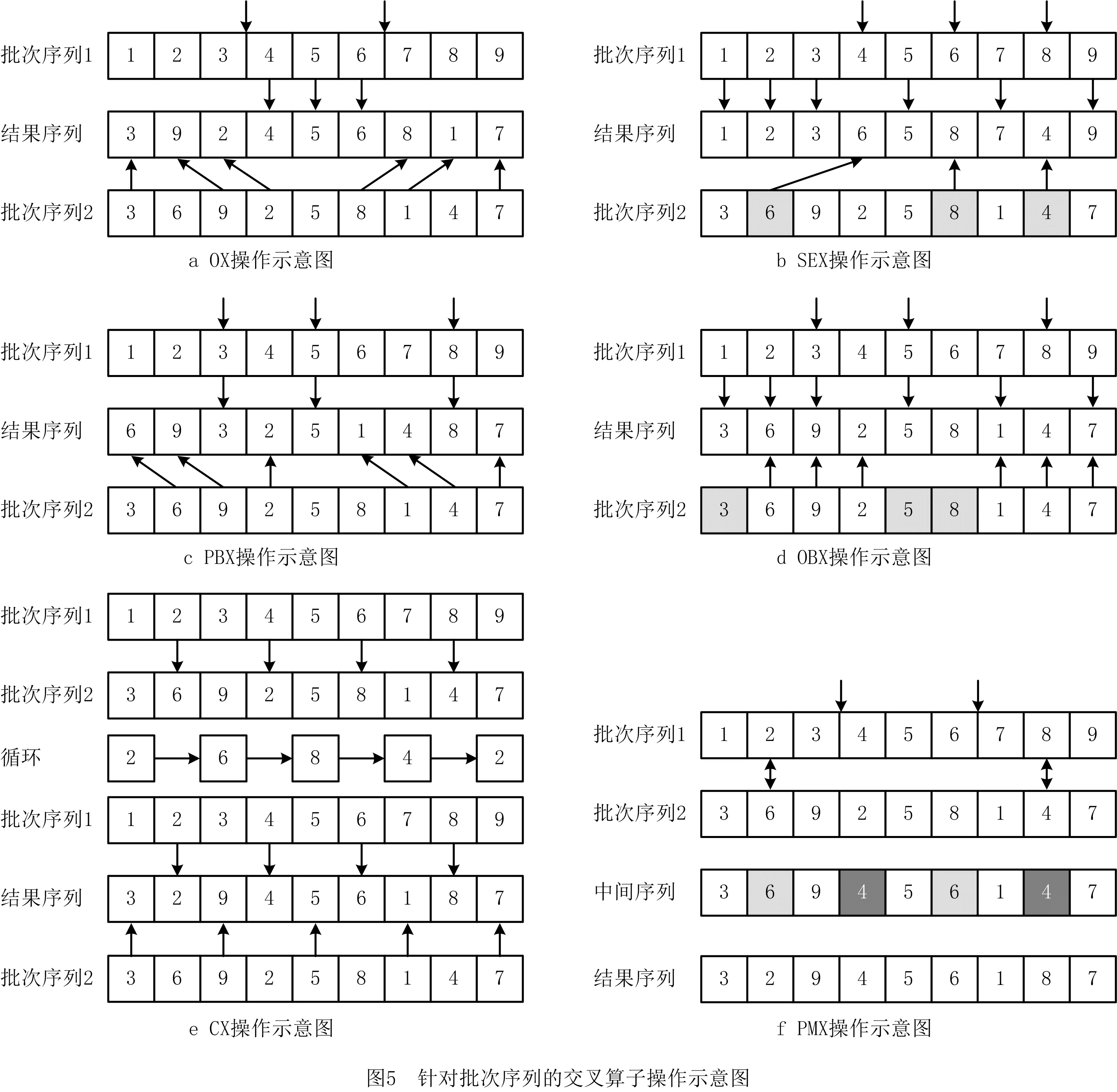
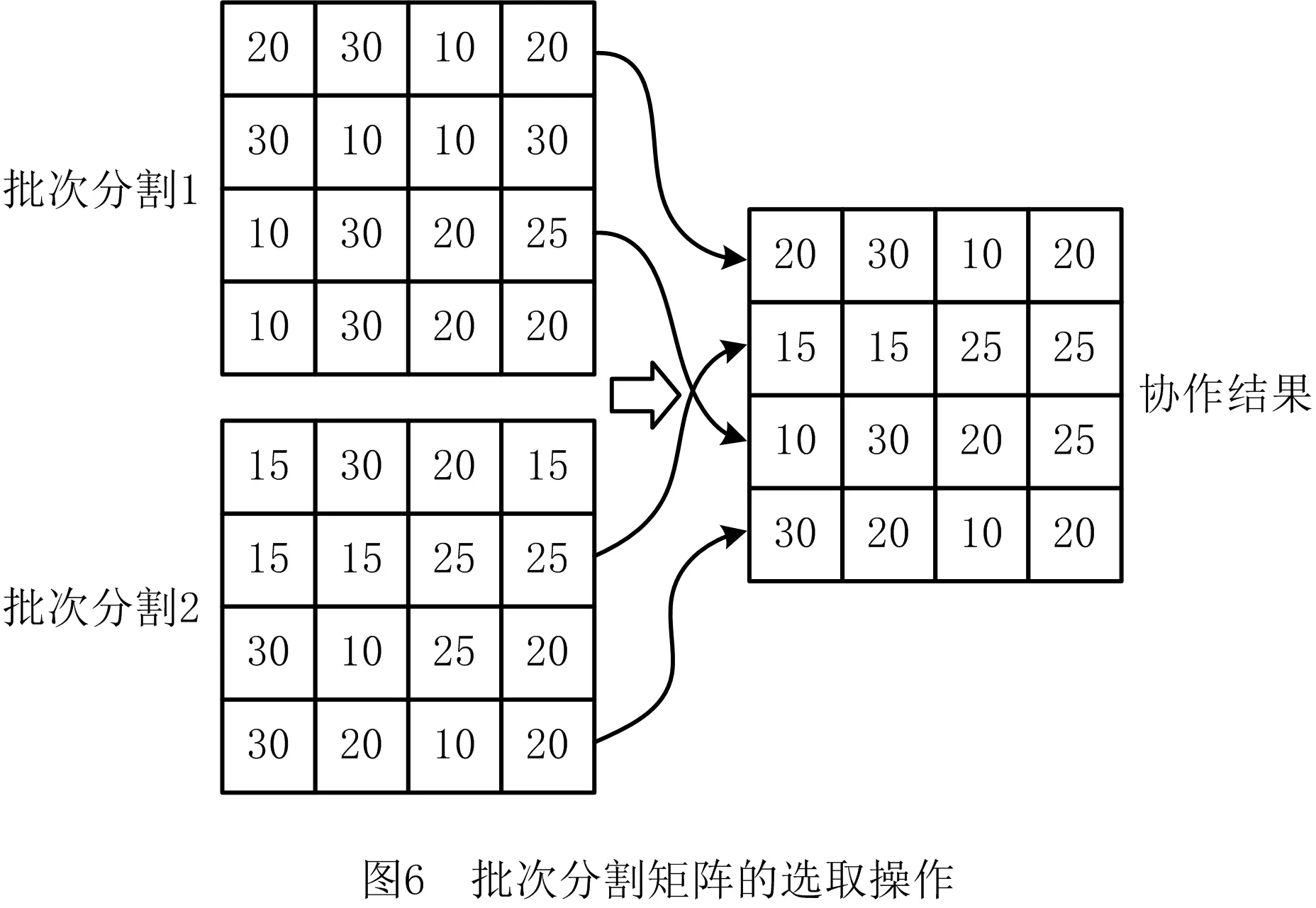
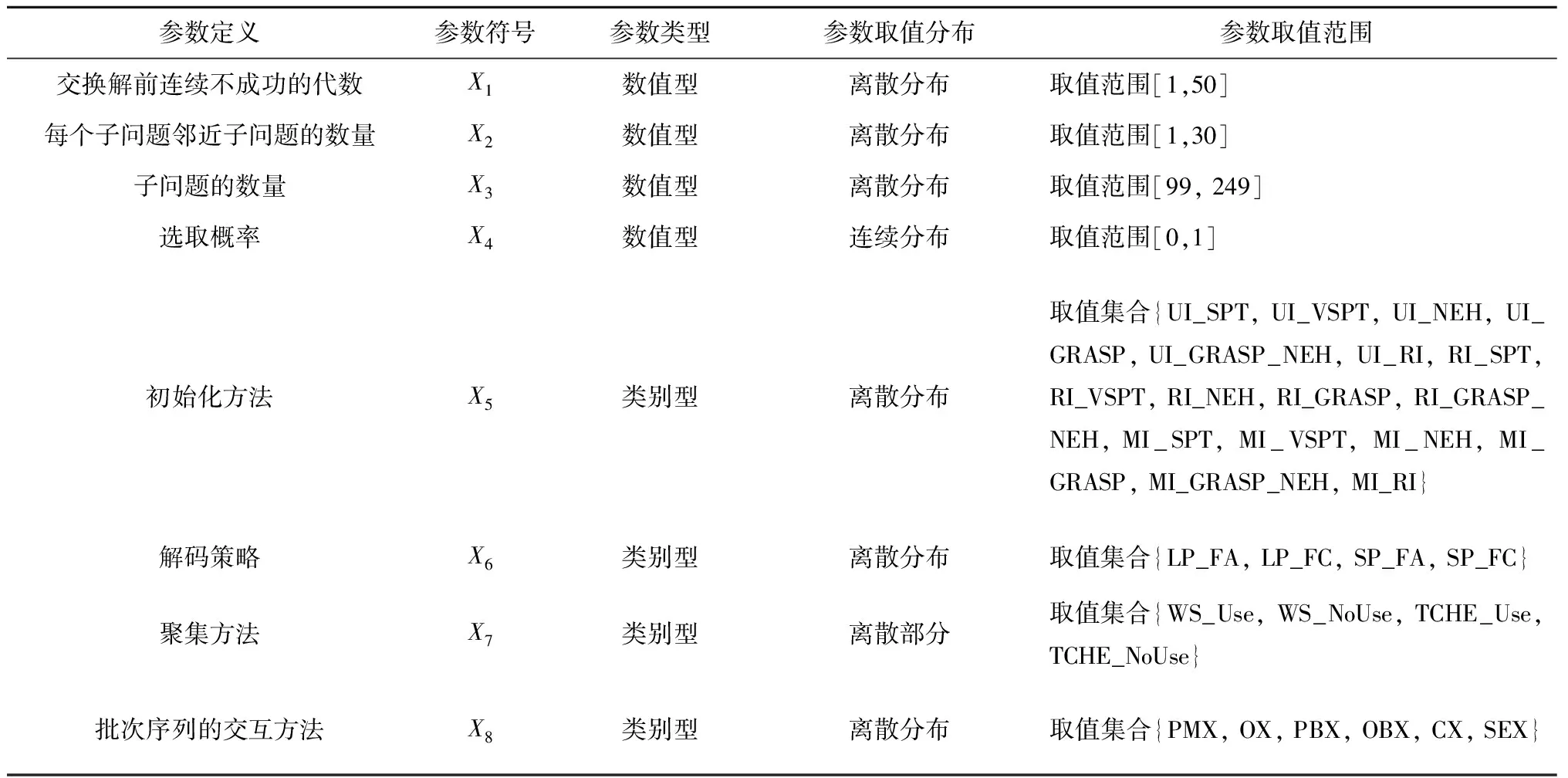
表3 可配置参数及其分布

由表3可知，在构建自动MOEA的过程中，有8个可配置的参数，标记为Xd，d=1,…,8。这些参数取值范围不同，其取值需要从相应的参数取值空间中采样。假设θ={x1,…,xd,…,xNparam}定义了一种算法配置，其中xd表示参数Xd的取值，同时假设Θ为所有的算法配置集合。当考虑使用I/F-Race来构建自动算法时，需要测试一组测试算例。设置c(θ)表示算法配置θ在测试算例集上的预期代价值。I/F-Race旨在找到具有最小代价值c(θ*)的最优算法配置θ*。

2.7 自动算法设计方法

I/F-Race作为一种机器学习方法，首次被应用于处理模型选择问题[15]，该方法包含多个F-Race流程。I/F-Race从一组有限的候选算法配置开始，在一组测试算例上进行测试。一个F-Race流程包含几个迭代步骤。在每个步骤中，候选配置将在单个测试算例上进行评估。在每个步骤之后，将那些在数理统计上比至少一个算法配置表现差的候选配置抛弃掉，剩下的算法配置将继续进行评估。为求解MOHFSP_VS，本文采用文献[13]所设计的F-Race的流程。算法1给出了I/F-Race算法流程，其中Race()表示F-Race流程。I/F-Race主要包括3个步骤：①根据给定的分布抽样新配置；②从新抽样的配置中选择最佳配置；③更新抽样分布使抽样偏向于最佳配置。具体流程见文献[16]。

算法1I/F-Race流程。

输入:I={I1,…,Ii,…IG}

参数空间:X={X1,…,X9}

总预算成本:B

1：Θk～SampleUniform(X)

2：Θelite:=Race(Θ1,B1)

3：j:=j+1

4：WhileBused≤Bdo

5: Θnew～Sample(X,Θelite)

6: Θj=Θnew∪Θelite

7: Θelite:=Race(Θj,Bj)

8:j:=j+1

9: EndWhile

输出:Θelite

3 实验设计

本章通过与其他4种高性能的MOEAs以及CPLEX进行比较，验证自动算法的有效性。对于MOEAs来说，在可接受的时间内获得满意解具有重要的实际意义，因此本文以运行时间作为算法终止准则，运行时间设置为n×m×tms，其中n为批次的数量，m为阶段数，t为一固定值。这种终止准则能够为规模大的测试算例提供更多的计算时间。本文中，t设置为200，在这种时间限制下，本文所比较的算法在大多数情况下都能够收敛。所有比较的MOEAs均采用C++语言编写，仿真实验运行在3.60 GHZ Intel Core i7处理器上。

3.1 测试数据和性能指标

本文收集了15个小规模算例和400个中大规模算例，每个测试算例用批次数量、阶段数和机器布局来标识。小规模算例中，批次数量n来自集合{3,5,8,10,12}，阶段数m来自集合{2,3,4}。这样，通过组合n和m，可得到15种不同的n×m。中大规模算例中，批次数量n来自集合{20,40,60,80,100}，阶段数m来自集合{3,5,8,10}。通过组合n和m，将得到20种不同的n×m。关于机器布局，本文采用了4种不同的类型，如下所示：

(1)第一阶段具有一台机器，其他阶段具有3台机器。

(2)第二阶段具有一台机器，其他阶段具有3台机器。

(3)第二阶段具有两台机器，其他阶段具有3台机器。

(4)所有阶段具有3台机器。

在中大规模算例中，通过组合4种不同机器布局的类型，会产生80种组合。对于每个组合，本文将随机生成5个测试算例，总共可以获得400个测试算例。在小规模算例中，为了直观地反映CPLEX和MOEAs的性能随问题规模增加而发生的变化，只组合类型(4)，对于每种组合，随机产生一个测试算例，总共得到15个测试算例。关于生产数据的生成，给出如下合理范围：每个批次的加工单元数量取自均匀分布U[50,100]，加工单元的加工时间取自均匀分布U[1,10],启动时间和运输时间分别由均匀分布U[50, 100]和U[10, 20]得出。另外，最大子批数量设置为30。

本文选择C-metric和D-metric两个性能指标[13]来评价MOEAs的性能。为了消除目标值不同量纲的影响，在度量中采用归一化处理。

3.2 算法调优阶段

为了进行全局的调优以确定最佳算法配置，从400个中大规模算例中随机选择100个具有不同问题规模的算例作为I/F-Race的测试算例。这100个算例构成了算法1中的测试集合I={I1,…,Ii,…IG}，它们的顺序是随机打乱的。本文将预算成本设置为实验的数量，一次实验是指利用一种算法配置求解一个测试算例。总预算成本B设为2000，每次F-Race流程中候选配置的最小保留数目设为10。表4给出了I/F-Race算法执行优化的过程数据。

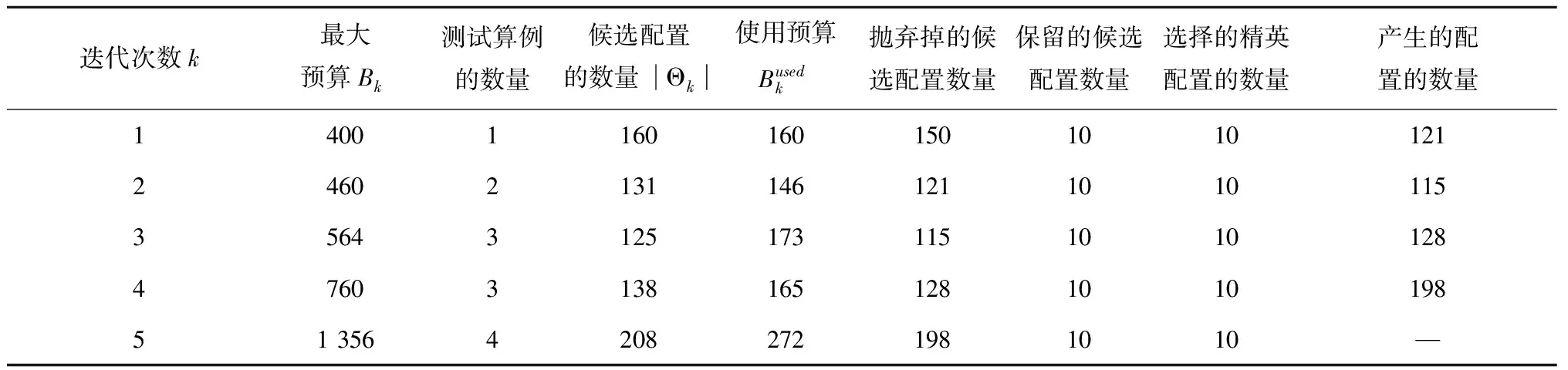
表4 I/F-Race中产生的过程数据

从表4可以看出，共存在5个迭代过程。随着迭代数的增加，每代的预算成本逐渐增加。同时，迭代1用到了一个测试算例，迭代2、3、4、5分别用到了2、3、3、4个测试算例。这意味着在迭代初期，精英配置和劣质配置比较容易识别，而在迭代后期，每个候选配置将需要更加细致地评估。这背后的原因是，在后续的迭代中生成的候选配置较为相似，因此需要更多的评估成本进行识别。

在测试了13个实例后，I/F-Race输出了10个精英配置，如表5所示。从表5可以看出，每个配置都不同于其他配置。这意味着高性能算法可以通过配置不同的参数值组合来构造。对于数值参数X1，10个精英配置的取值均大于1，这也证明了MDABC算法中重启策略的有效性。对于数值参数X4，可以看出，在10个精英配置中，有9个配置取值大于0.5，这说明在执行交互操作的时候，选择优良解中的信息更有利于寻优。对于类别参数X5，可以看出，所有配置都选择了RI来初始化批次分割矩阵，这证明RI表现明显优于其他两种方法。在初始化批次排列时，9个精英配置选择了RI来进行初始化，只有一种配置选择了VSPT，从而说明了RI方法的有效性。对于类别参数X6，所有精英配置均使用FA策略来选择机器，这说明FA比FC更适合解决本文问题。所有配置使用SP策略来执行批次排序，这是因为SP比LP更好地利用了批量流的特性。对于类别参数X7，所有算法配置均采用了加权和方法，同时均使用了目标归一化。这证明了加权和方法以及目标归一化为更加适合MOHFSP_VS的适应度值评估方法。对于类别参数X8，10种精英配置中，出现了5个配置选择了PBX，3个配置选择了OBX，而TPX和CX各被1个配置选中。在接下来的算法测试阶段，将使用最优的算法配置来构造自动算法求解MOHFSP_VS，即X1=21，X2=10，X3=245，X4=0.7，X5=RI_RI，X6=FA_SP，X7=WS_USE，X8=PBX。

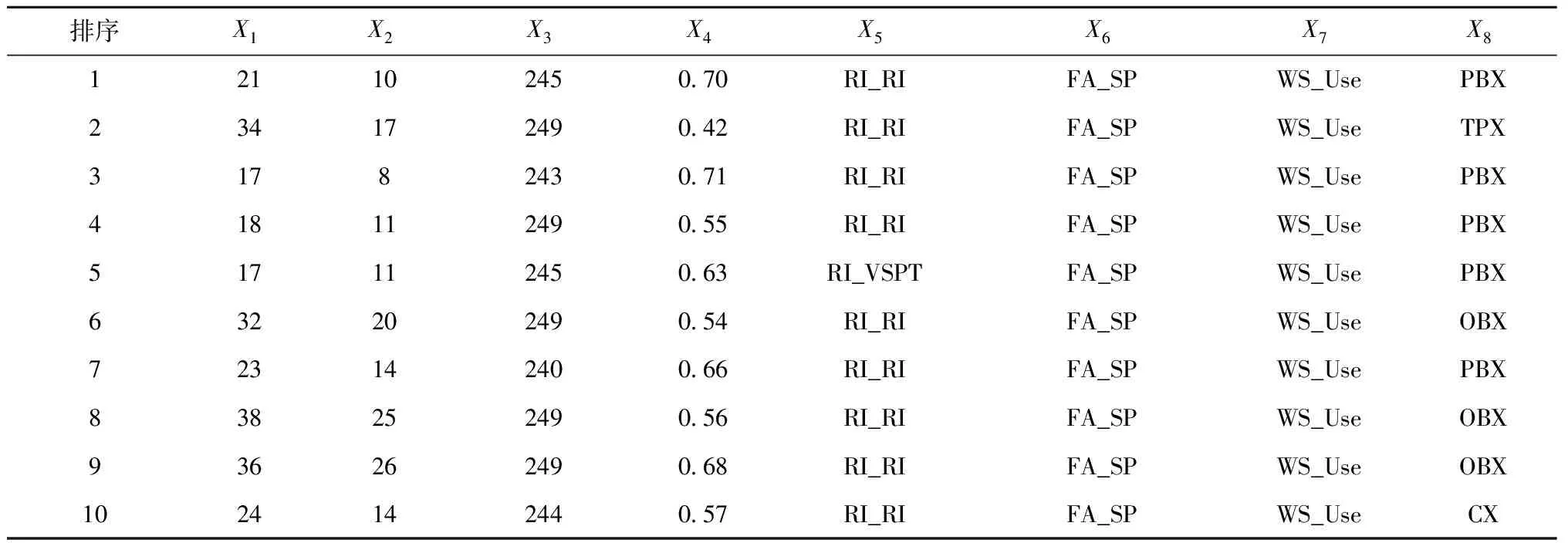
表5 输出的10个精英配置

3.3 算法测试阶段

为了评估由AAD自动构建的MOEA的性能，将其与现有文献中的4种MOEAs进行比较，分别是MOCGWO[26]、MOEA/D[24]、PHMOEA/D[27]和NSGA-II[28]。选择它们作为比较对象的原因如下：①MOEA/D和NSGA-II是解决多目标调度问题和其他各种多目标优化问题的著名算法框架；②MOCGWO和PHMOEA/D已被证明在解决多目标HFSPs时性能是优异的，另外它们采用的解编码都是两层的，适合MOHFSP_VS的求解。本文也对比较算法中的参数进行了适当的设置。对于PHMOEA/D中的数值参数，本文采用文献中所建议的田口法[25]进行设置。对于MOCGWO、MOEA/D和NSGA-II中的数值参数，在对应的文献中没有找到具体的配置方法。因此，首先确定其数值参数的合理取值范围，然后通过田口法进行配置。对于比较算法中的类别参数，为了进行公平的比较，所有比较算法都采用了本文所提出的编码方案。在此基础上，对于其他的类别参数，即初始化方法、解码策略、聚集函数方法、目标归一化以及交叉算子，则根据表5输出的最佳配置中出现的大多数进行设置。

3.3.1 MOEAs算法与CPLEX在小规模数据集上的对比分析

对于每个算例，分配20个均匀分布的权重，CPLEX通过对两个目标线性加权的方式独立运行20次，每次运行的时间限制设置为3 600 s。通过收集20次运行的解，得到一组非支配解。对于MOEAs，针对每个测试算例，独立运行5次，每次运行时间设置为n×m×200 ms。表6和表7分别展示了基于C-metric和D-metric指标的平均值(AVG)和标准差(SD)。此外，表7中还展示了MOEAs和CPLEX求解每个算例的运行时间。

对比AAD算法和CPLEX，基于C-metric指标，从表6可以看出，CPLEX在问题3×2和3×3上取得了较大的C-metric均值，但随着问题规模的增加，AAD算法在其他所有问题上均取得了更大的C-metric均值。对比于CPLEX的0.056，AAD算法取得了明显大的总体平均值0.430。基于D-metric指标，从表7中可以看出，AAD算法在问题3×3上取得了更小的D-metric均值，这说明AAD算法在3×3问题上得到的Pareto解在解集上分布更加均匀。除了问题3×2，AAD算法在其他问题上均取得了更小的D-metric均值，并取得了更小的总体平均值0.107。此外，从表7中可以看出，随着批次和阶段数量的增加，由于问题的NP难特性，从问题5×2开始，所有权重下，CPLEX在3 600 s的运行时间内都不能获得最优解。同时，MOEAs的运行时间远小于CPLEX。通过这些观察，可以得出结论，利用CPLEX求解混合整数规划模型很难得到包含所有最优Pareto解的Pareto解集。此外，CPLEX的运行时间是难以接受的。综上所述，对比于传统的数学规划求解方法，MOEAs的优越性是可以得到体现的。与其他MOEAs相比，基于C-metric，AAD算法在所有问题上均可以取得较大的均值。在所有问题上，根据C-metric结果，MOEA/D、PHMOEA/D和NSGA-II这3种算法所获得的Pareto解全部可以被AAD算法得到的Pareto解所支配。基于D-metric的均值，AAD算法同样在所有问题上表现最好。由此说明，AAD算法在小规模测试算例上取得的Pareto解集具有良好的收敛性和高效性。通过与CPLEX和其他MOEAs的对比，在小规模数据集上，AAD算法的高效性和优越性是可以得到验证的。

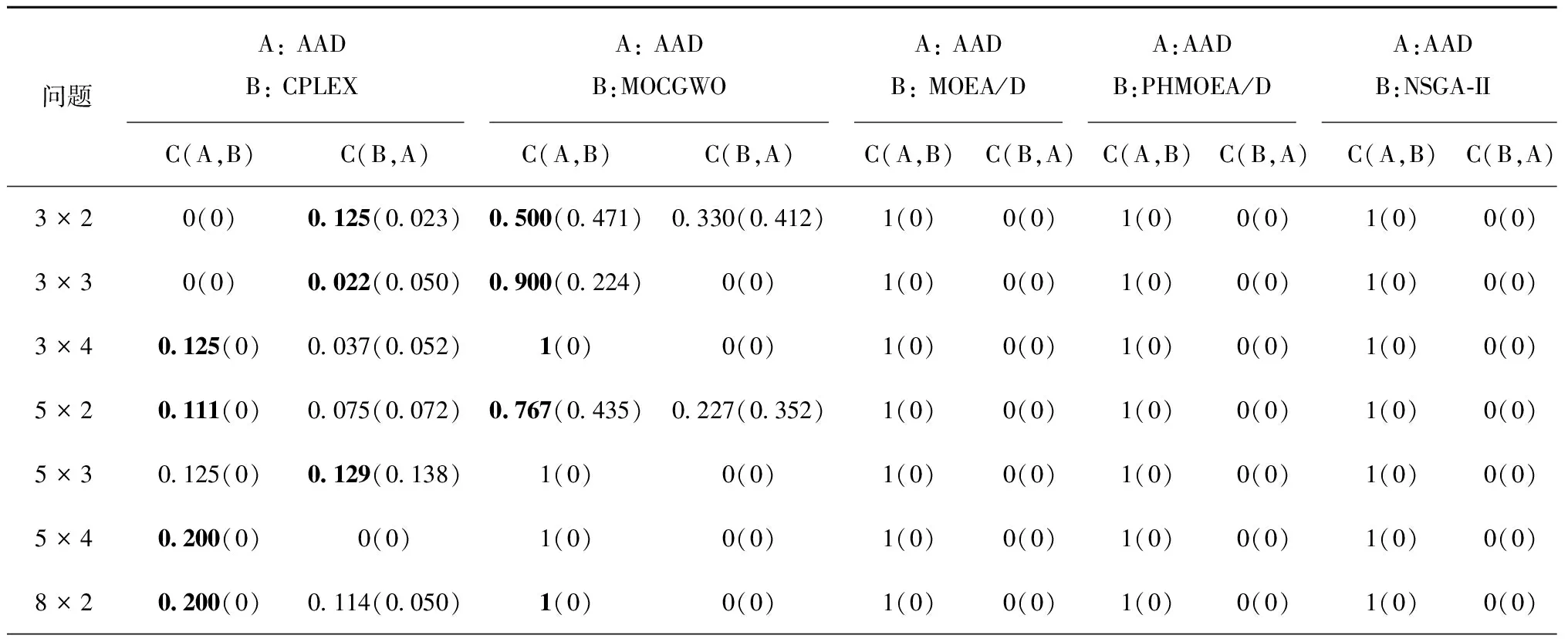
表6 小规模数据集上C-metric AVG(SD)值对比

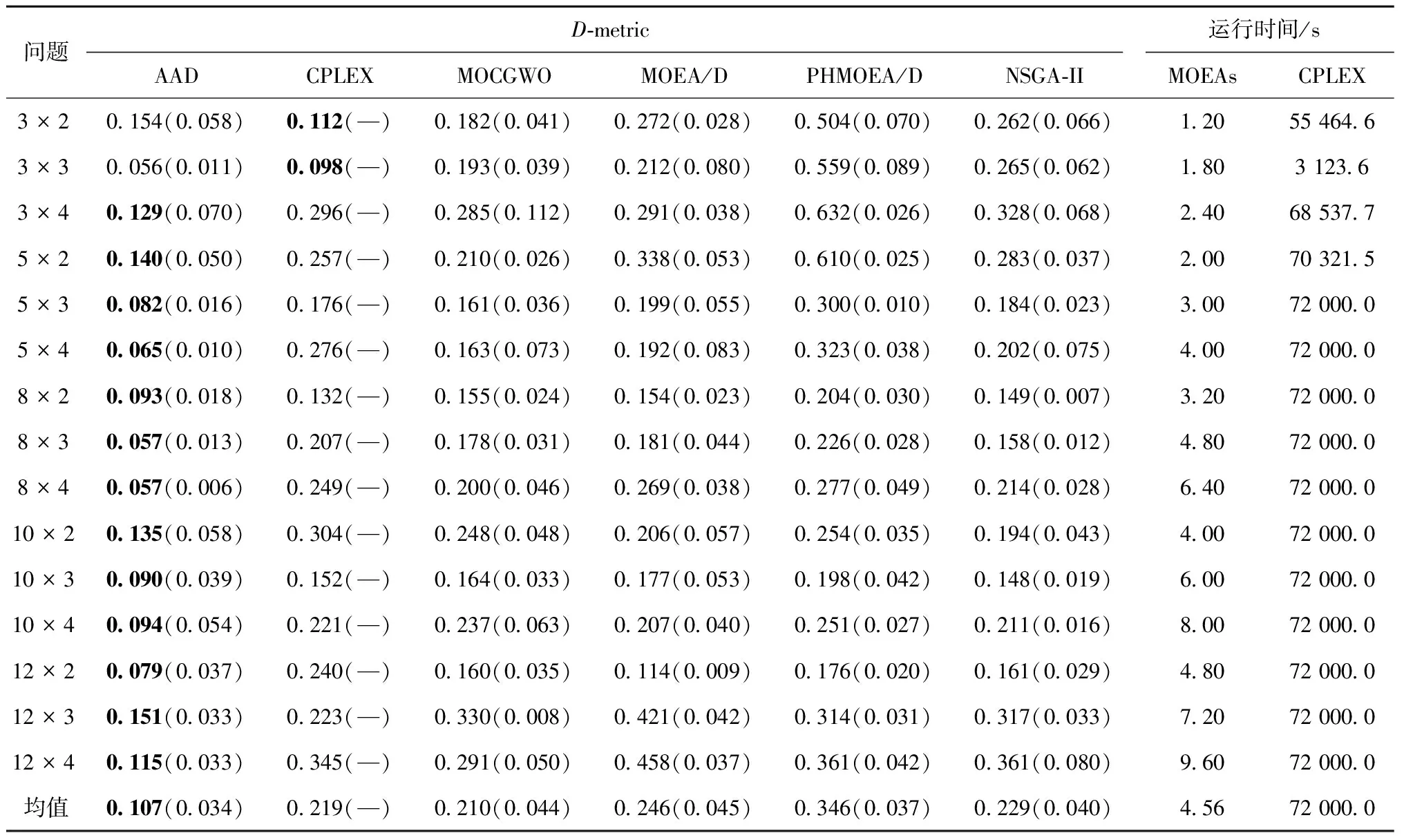
表7 小规模数据集上D-metric AVG(SD)值对比

3.3.2 MOEAs算法在中大规模数据集上的对比分析

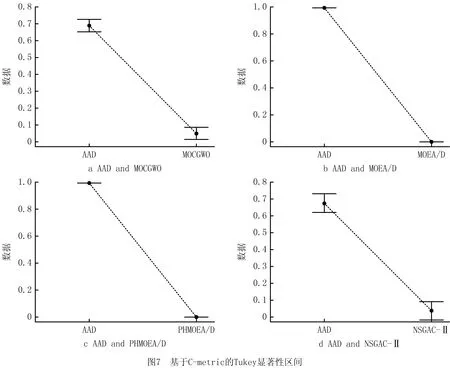
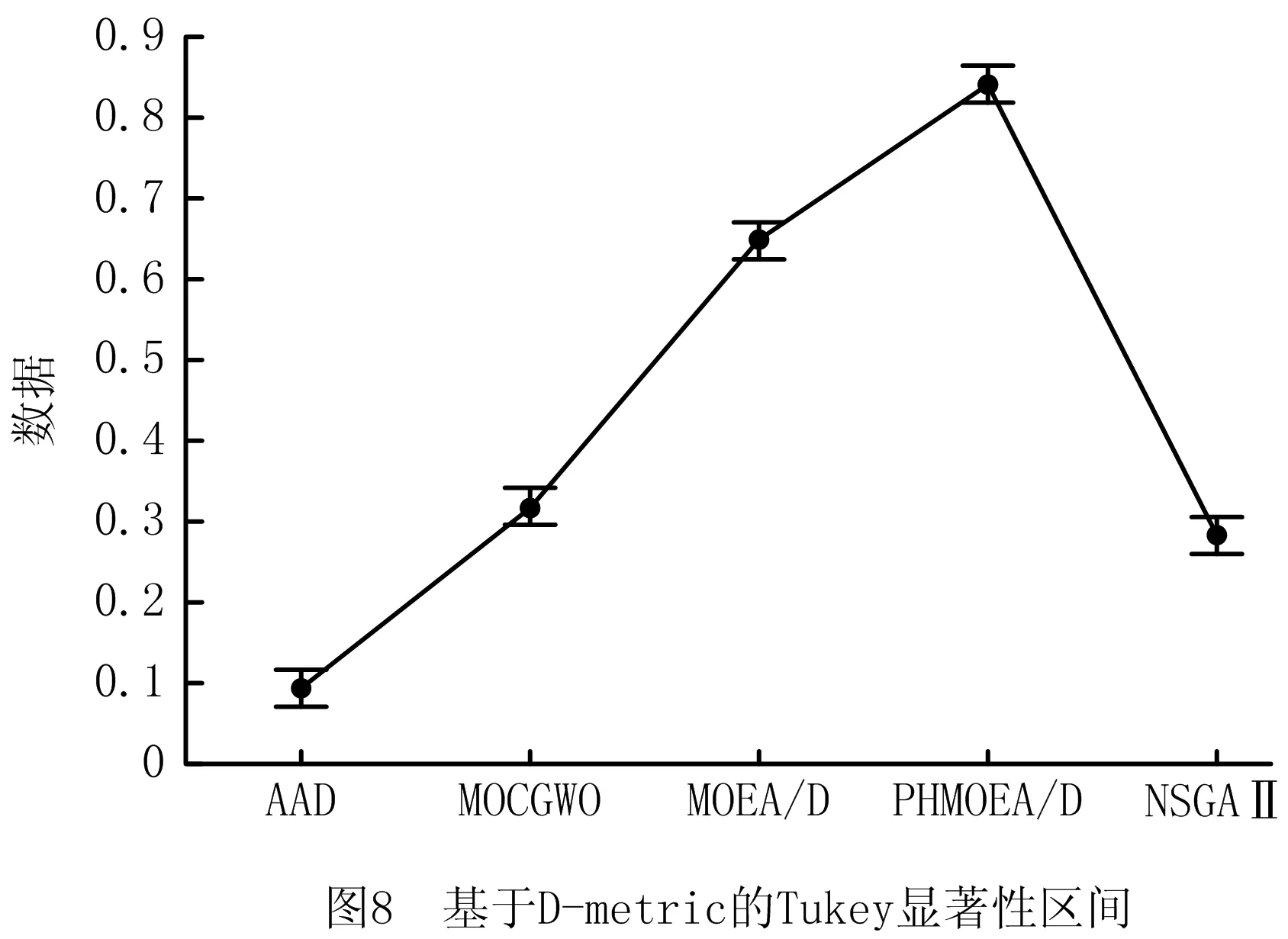
对于中大规模数据集上的每个测试算例，分别计算得到C-metric和D-metric的平均值和标准差。然后在相同的问题规模下，再次进行平均，结果统计在表8和表9中。此外，为了验证C-metric和D-metric结果的统计有效性，采用单因素方差分析(ANOVA)对平均值进行分析。图7和图8分别显示了在95%置信水平上C-metric和D-metric结果的Tukey HSD区间图。在区间图中，若两种算法之间没有重叠，则它们之间存在统计意义上的显著差异。

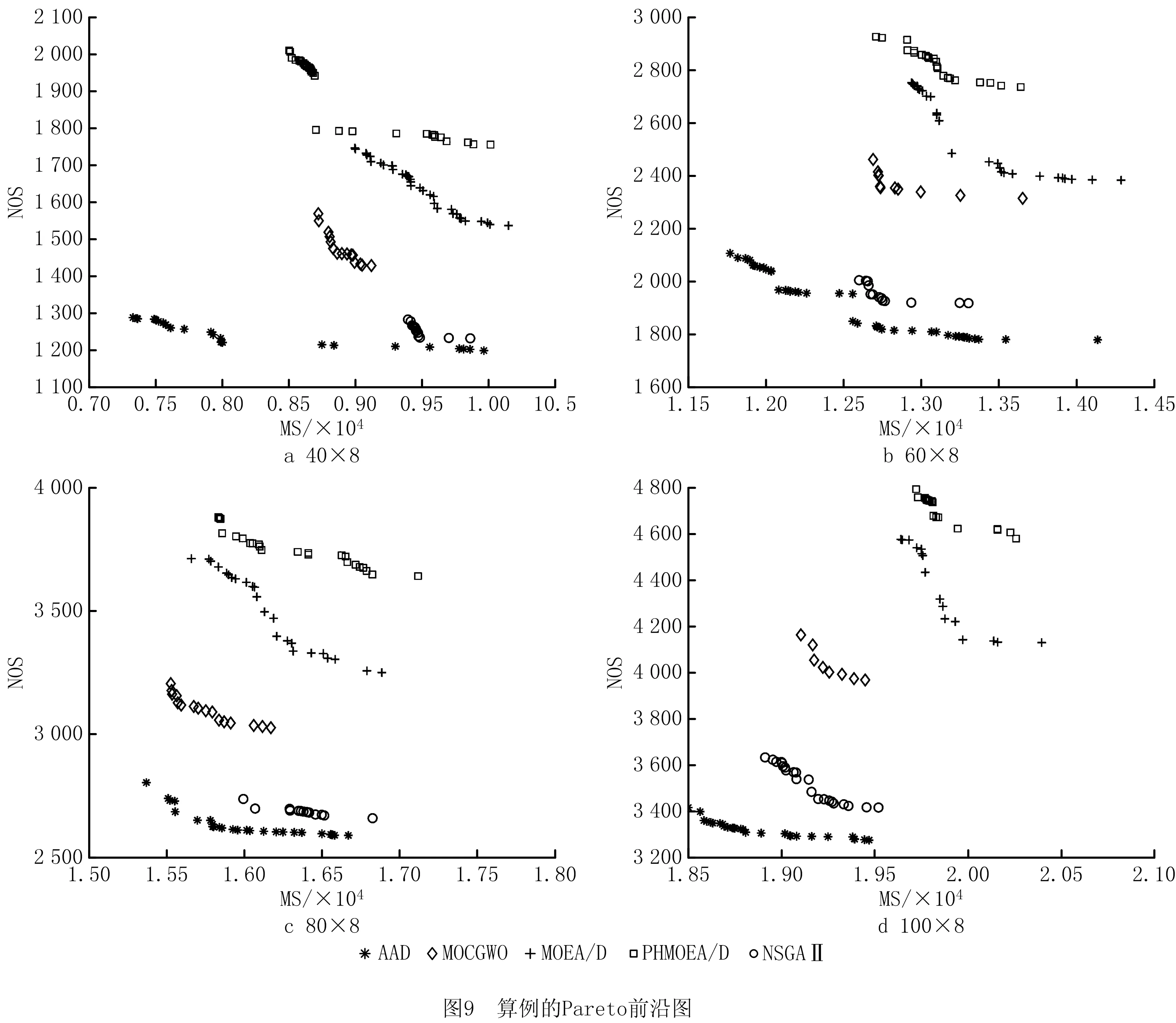
根据表8中展示的C-metric结果可以看出，对于所有的15个问题，AAD相对于其他任何算法得到的C-metric均值都是最大的，并且所获得的总体平均值远远大于其他算法。该结果意味着，AAD算法获得的Pareto解中有很少一部分会被其他算法的Pareto解所支配，而其他算法获得的Pareto解中大部分会被AAD算法所获得的Pareto解所支配。由此证明AAD算法的收敛性在所有MOEAs中是最好的。从图7中可以看出，基于C-metric均值数据，AAD算法在数理统计上明显优于其他4种算法。对于C-metric标准差，可以看出AAD算法得到的值总是大于其他算法得到的值。这是因为其他算法得到的Pareto解很难支配AAD所取得的Pareto解。因此，其他算法得到的C-metric标准差值总是比AAD算法小。基于D-metric比较，从表9中可以看出，AAD的总体平均值(0.093)远小于MOCGWO(0.317)、MOEA/D(0.648)、PHMOEA/D(0.842)和NSGA-II(0.282)。由图8可以看到，根据显著性分析结果，AAD再次明显优于其他4种算法。由此证明AAD取得的Pareto解集不但具有最好的收敛性，而且解集的分布性也是最好的，所得的Pareto解集更加逼近真实的Pareto前沿。从D-metric标准差值来看，AAD算法对于大多数问题是能够得到最小值的，这可以说明AAD算法具有良好的鲁棒性。为了更加直观、清晰地展示它们的性能，图9展示了所有算法针对4个不同问题规模测试算例得到的Pareto解集。图9显示AAD算法的确可以得到质量更好且分布更加均匀的Pareto解，这与数值分析所得的结论是一致的。综上所述，AAD算法在解决MOHFSP_VS时的性能是优越且高效的。

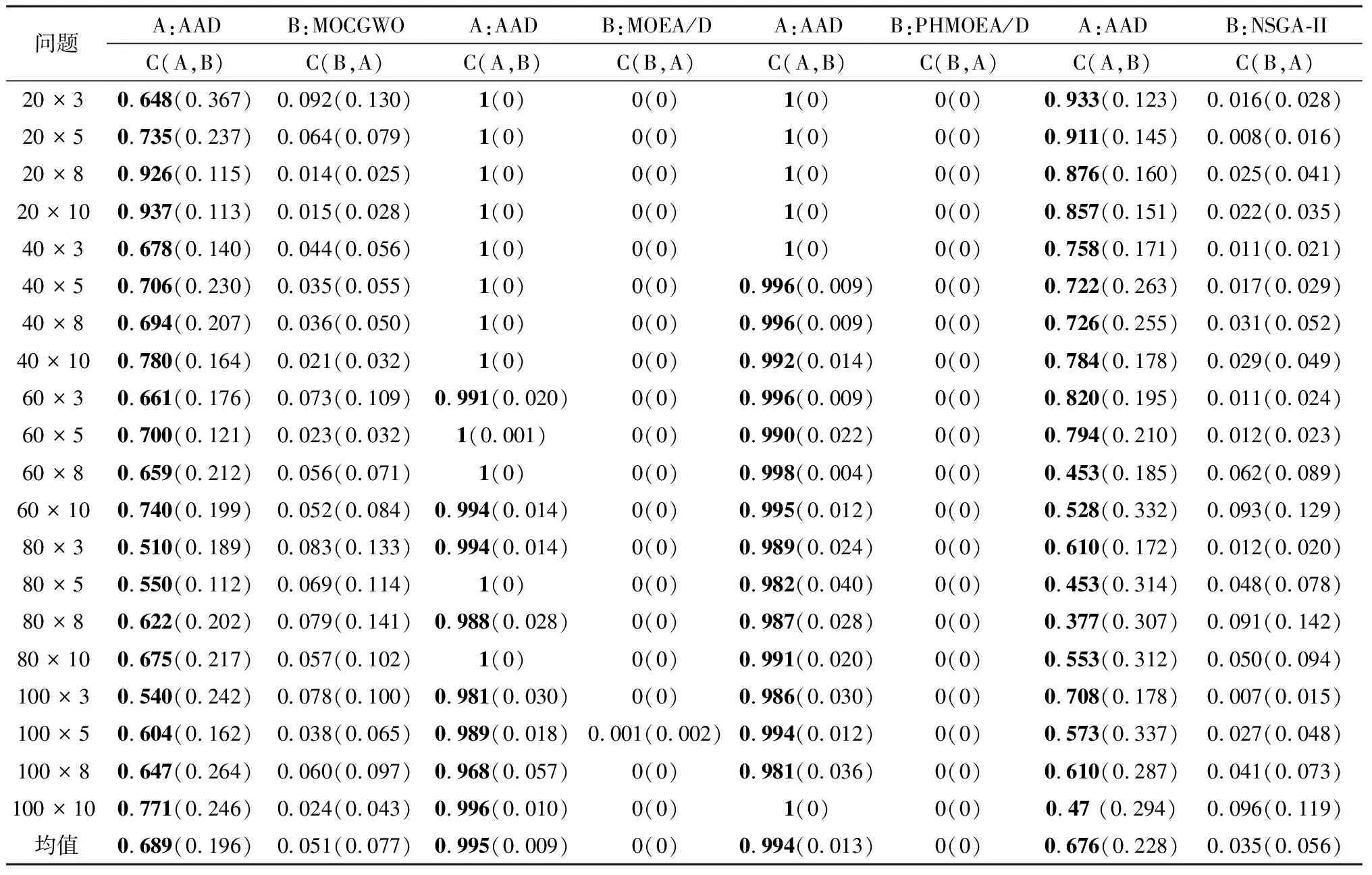
表8 中大规模数据集上C-metric AVG(SD)值对比

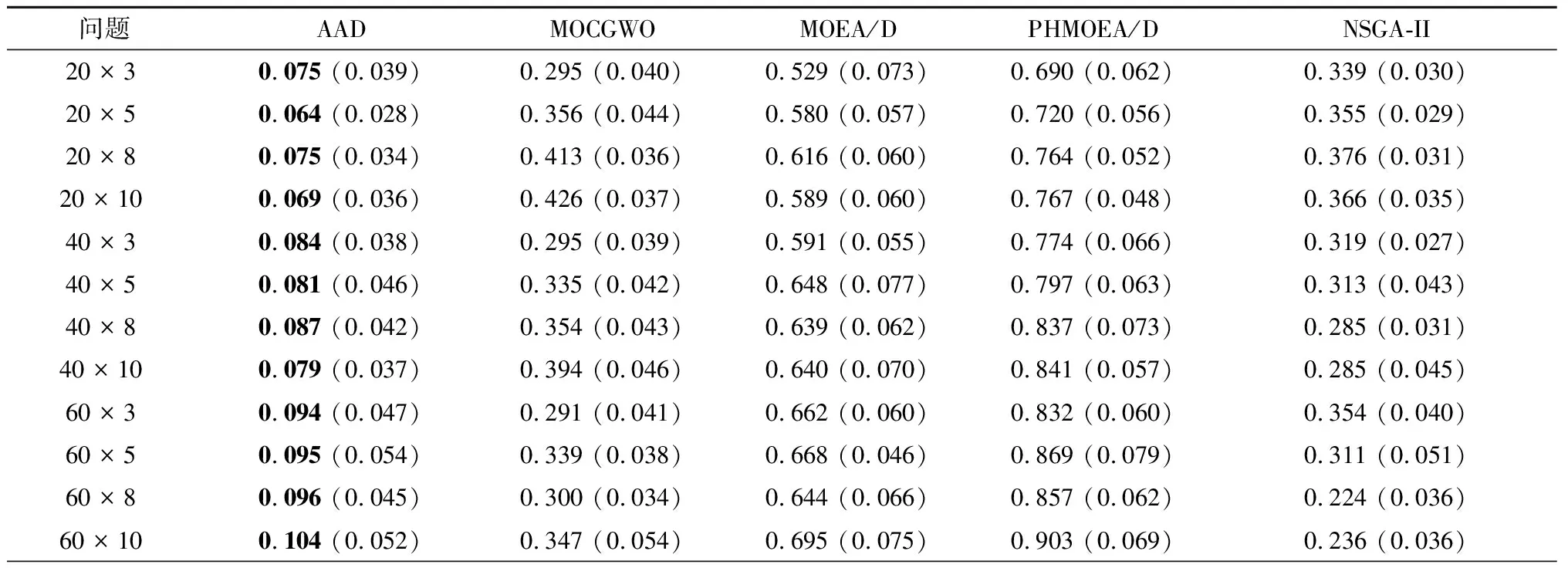
表9 中大规模数据集上D-metric AVG(SD)值对比

4 结束语

考虑变分批技术，本文研究了以最小化最大完工时间和子批总数为目标的MOHFSP_VS，并考虑了启动和运输操作。建立了一个多目标混合整数规划模型，并通过求解CPLEX模型来评估两个目标间的权衡关系。为了求解该一问题，本文在MDABC算法框架的基础上，引入了AAD方法来自动构造高性能的MOEA。针对问题特性，提出了动态解码策略；针对具体问题特征和算法框架，对于可配置类别和数值参数，给出了合理的取值区间；对于AAD方法，采用了I/F-Race方法；最后，通过实验证明，自动生成的MOEA表现是非常突出的。

对于MOHFSP_VS，未来的研究包括：①设计更高效的编码和解码策略；②基于问题特性开发启发式规则进一步改进结果；③评估一些其他目标(例如总流经时间，总提前和延迟时间，和机器利用率等)；④考虑车间动态事件的影响，研究动态和重调度策略。对于AAD方法，笔者将尝试将算法框架视为一个可配置参数，则具体参数将隶属于算法框架，重新定义算法配置问题和I/F-Race流程。