基于自适应模糊神经网络的机器人焊接焊缝外形预测方法

陶 永，兰江波，任 帆，王田苗，江 山，高 赫，温宇方

(北京航空航天大学 机械工程及自动化学院，北京 100083)

0 引言

焊缝的表面质量对焊缝性能有重要影响，焊缝表面质量例如外形尺寸是否平滑均匀，有无缺陷等都是评价焊缝质量的指标[1]。当前机器人焊接工艺复杂，在焊接过程中，焊接质量影响因素众多。机器人焊接参数的异常波动、机器人的震动、焊接参数的选择和焊接设备的操作规范，都会影响最终的焊接质量[2]。

钛合金的机器人焊接质量检测主要包括焊接接头的力学性能[3-5]、表面焊接缺陷[6-8]和外表尺寸[9-10]等。但是机器人焊接质量与焊接工艺参数之间的对应关系目前还难以定量描述。针对这一问题，国内外学者开展了广泛的研究，如LI[11]等建立了多工艺参数与焊缝成形质量之间的基本多元线性回归模型，描述了工艺参数与焊缝成形质量之间的关系；Gou等[12]根据全熔透焊接过程中熔池的流动行为确定了对接焊接的最佳焊接参数；CASALION等[13]利用人工神经网络将焊缝凸度和深度与焊接工艺参数进行关联，建立了选择最合适的激光焊接工艺的模型。随着人工智能的快速发展，人工神经网络逐步应用到机器人焊接质量预测的研究中。LI等[14]利用人工神经网络和随机森林模型对焊缝质量水平进行预测；BUFFA等[15]采用有限元模型预测试件间接触界面上主要场变量的局部值，并将其作为神经网络的输入，识别和预测3种不同的焊接质量水平；黄晔[16]提出利用BP神经网络对焊缝缺陷进行建模识别；CHI等[17]提出利用模糊径向基神经网络对等离子弧焊进行多质量预测，解决了BP神经网络耗时长的问题，但是其非线性性能不如BP神经网络；SHAO等[18]提出一种用光学传感器和神经网络技术对激光点焊过程进行自动检测的方法，该方法有助于微电子行业的焊接质量检测，但针对大型构件的适用性还有待验证；KHALID等[19]提出利用人工神经网络预测两种金属间的最佳焊接参数，但是对同种金属之间的焊接效果尚有待验证；ZHAO等[20]通过研究焊接过程中不同焊接电流和电压下焊接功率信号的特点，从中提取特征点描述曲线形状，建立预测模型。人工神经网络自提出至今的60年里，其理论和应用方面的研究均得到了极大的发展，并在许多领域中得到广泛应用[21]。但神经网络的理论体系并不完善，例如神经网络模型是一个“黑箱”模型，网络权值随机选取，网络参数缺乏明确的物理意义，建立的模型难以理解等。模糊算法能够表达模糊知识，实现模糊推理，可有效弥补神经网络的不足[22-23]。

本文面向钛合金的T型焊缝外表尺寸的预测，将模糊理论与神经网络相结合，提出建立一种基于直觉模糊C均值聚类和优化粒子群算法相融合的自适应模糊神经网络算法，对焊接参数与焊缝外形特征之间的关系进行拟合，对钛合金焊接机器人焊缝的焊脚宽度和焊高高度进行预测，进而持续优化焊接工艺数据库，并为后续的参数优化提供支持。该方法相比于传统试焊法，可根据输入的焊接参数对焊后外形进行预测，避免了由于人工试焊造成的材料浪费，降低了成本，并提高了加工效率。

1 T-S模糊神经网络

美国加州大学的ZADEH[24]教授在1965年首次提出一种用来表达事物模糊性质的重要概念——隶属函数，突破了经典几何理论，奠定了模糊理论的基础。TAKAGI等[25]于1985年的模糊推理模型——Takagi-Sugeno(T-S)模型，T-S模型是一种自适应性很强的模糊系统，该系统可自动更新隶属函数的参数值。基于T-S模型的模糊神经网络分为输入层、模糊化层、模糊规则计算层和输入层4层。

基于典型的T-S模糊系统，本文提出的焊缝外形预测模糊神经网络方法，可用如下“if-then”规则进行定义：

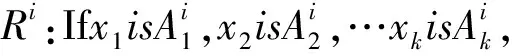
(1)

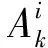
对于焊接参数输入量x=[x1，x2，…xk]T，本文选择激光功率、焊接速度、送丝速度和保护气体流量作为系统的输入参数。首先，根据焊接模糊规则计算各输入变量的焊接参数隶属度：

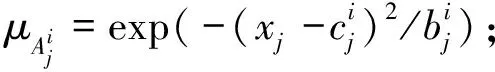
j=1,2,…k；i=1,2…n。

(2)

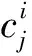
将各焊接参数隶属度进行模糊计算，采用模糊算子为连乘算子：

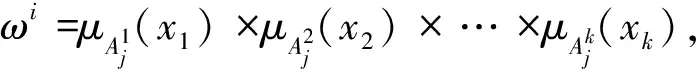
i=1,2…n。

(3)

最后，根据模糊计算结果计算焊缝宽度/高度的输出值：

(4)

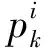
(5)

式中:yd是网络期望焊缝焊宽/焊高输出；yc是网络实际焊缝焊宽/焊高输出；e是期望输出和实际输出的误差。

(6)

(7)

式中:α为网络学习率；xj为网络输入焊接参数；ωi为输入焊接参数隶属度连乘积。

在机器人焊接的焊缝外形预测模糊神经网络中，焊接参数隶属函数的中心和宽度称为前件参数，输出的权重系数称为后件参数。在传统模糊神经网络中，采用梯度下降法和BP法的混合算法更新网络参数，但是这种算法具有收敛速度不确定，且容易陷入局部极小值的不足。因此，为了获得更准确的前件参数，提高网络的识别精度，本文提出一种利用直觉模糊C均值和自适应权重粒子群算法(Intuition Fuzzy C-Means self-Adaptive Particle Swarm Optimization，IFCM-APSO)相融合的方法，对隶属函数的中心和宽度参数进行寻优计算。

2 基于改进自适应模糊神经网络的机器人焊接焊缝外形预测方法

本文提出一种基于IFCM-APSO算法的自适应模糊神经网络方法，所用算法结构简单，有助于使前件参数的辨识更加简洁有效。

1984年，BEZDEK等[26]提出了模糊C均值聚类算法(Fuzzy C-Means，FCM)，引入样本到聚类中心的隶属度，通过优化目标函数得到每个样本点对类中心的隶属度，决定样本点的类属以达到自动对样本数据进行分类的目的。1995年，EBERHART等[27]提出一种粒子群优化(Partical Swarm Optimization, POS)算法，该算法具有群体智能、迭代格式简单、可快速收敛得到最优解所在区域等优点，迄今为止FCM算法和PSO算法都得到了较好的应用。但是在利用PSO算法确定焊接参数隶属度函数宽度的过程中，较大的权重因子有利于跳出局部最小点，便于全局搜索，而较小的权重因子则有利于对当前的搜索区域进行精确的局部搜索。

针对钛合金带筋壁板的机器人焊接过程中焊缝外形预测的问题，传统模糊神经网络在前件参数的确定过程中容易发散，本文提出IFCM-APSO算法对其进行改进，该算法在确定前件参数过程中从两个方面对传统梯度下降法进行改进：一方面引入非隶属度和犹豫度使得隶属度矩阵更加合理，便于对焊接过程中由于参数波动带来的噪点进行聚类；另一方面在确定隶属函数宽度的过程中，采用一种自适应权重算法对粒子群算法进行改进(self-AdaptiveParticle Swarm Optimization，APSO)，以利于算法收敛，使其能够对焊接参数的隶属函数宽度进行寻优计算。

首先，引入焊接直觉模糊集(Welding Intuition Fuzzy Set，WIFS)，WIFS是传统模糊集的重要拓展，其中增加了焊接参数非隶属度γ和不确定度π，假设焊接直觉模糊集A表示焊接参数样本x与论域X={x1，x2，…，xn}的关系，则有：

A={μA(x)，γA(x)，πA(x)|x∈X}。

(8)

当满足条件μA(x)→[0,1]和γA(x)→[0,1]且0≤μA(x)+γA(x)≤1时，焊接参数样本的不确定度可表示为：

πA(x)=1-μA(x)-γA(x)。

(9)

为了将焊接直觉模糊特征与传统的模糊聚类方法相结合，将焊接直觉模糊隶属度定义为：

(10)

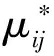
(11)

πij=1-μij-(1-μij)/(1+λμij)。

(12)

由此，使用焊接参数直觉隶属度矩阵，可以得到新的焊接参数聚类中心公式：

(13)

当焊接参数聚类中心更新时，隶属度矩阵也将被更新。在每次迭代的过程中，焊接参数聚类中心的隶属度矩阵的数值都会更新一次，直到前一次的隶属度矩阵和更新后的隶属度矩阵的插值小于设定阈值，此时迭代过程结束，聚类中心达到最优。适应度函数如下：

(14)

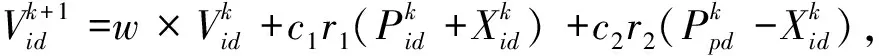
焊接动态惯性权重系数，按如下公式进行更新：

(15)

式中：ωmax和ωmin分别表示ω的最大值和最小值，f表示微粒当前的目标函数值，favg和fmin分别表示当前所有微粒的平均目标值和最小目标值。

IFCM-APSO目标函数的公式可表示为：

(16)

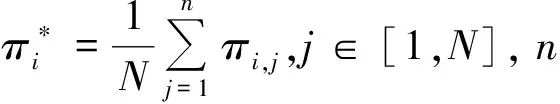
综上所述，IFCM-APSO算法计算焊接参数隶属函数中心的步骤，可归纳如下：

(1)利用随机数发生器对焊接参数的隶属度矩阵赋予初值。

(2)引入不确定度，将焊接参数隶属度矩阵变为模糊隶属矩阵。

(3)使用模糊隶属度矩阵计算待分类焊接参数到聚类中心的距离，将样本划分到各个类中。

(4)重新计算每个类的聚类中心、焊接参数样本到聚类中心的距离。每次计算都使用直觉模糊隶属度矩阵代替原有的隶属度矩阵，并将样本重新划分到各个类中。

(5)以式(16)为目标函数进行迭代，寻找隶属度函数的最佳宽度。

(6)重复(2)～(5)步，直到适应度函数达到指定阈值。

通过上述步骤，可得到高斯函数的中心值和宽度值。该算法在运用过程中相比传统的梯度下降算法，引入了不确定度的概念，能更好地优化焊接参数数据集中噪点的分类情况，同时避免在迭代过程中陷入极小值。

优化后的隶属度函数图像如图1所示。

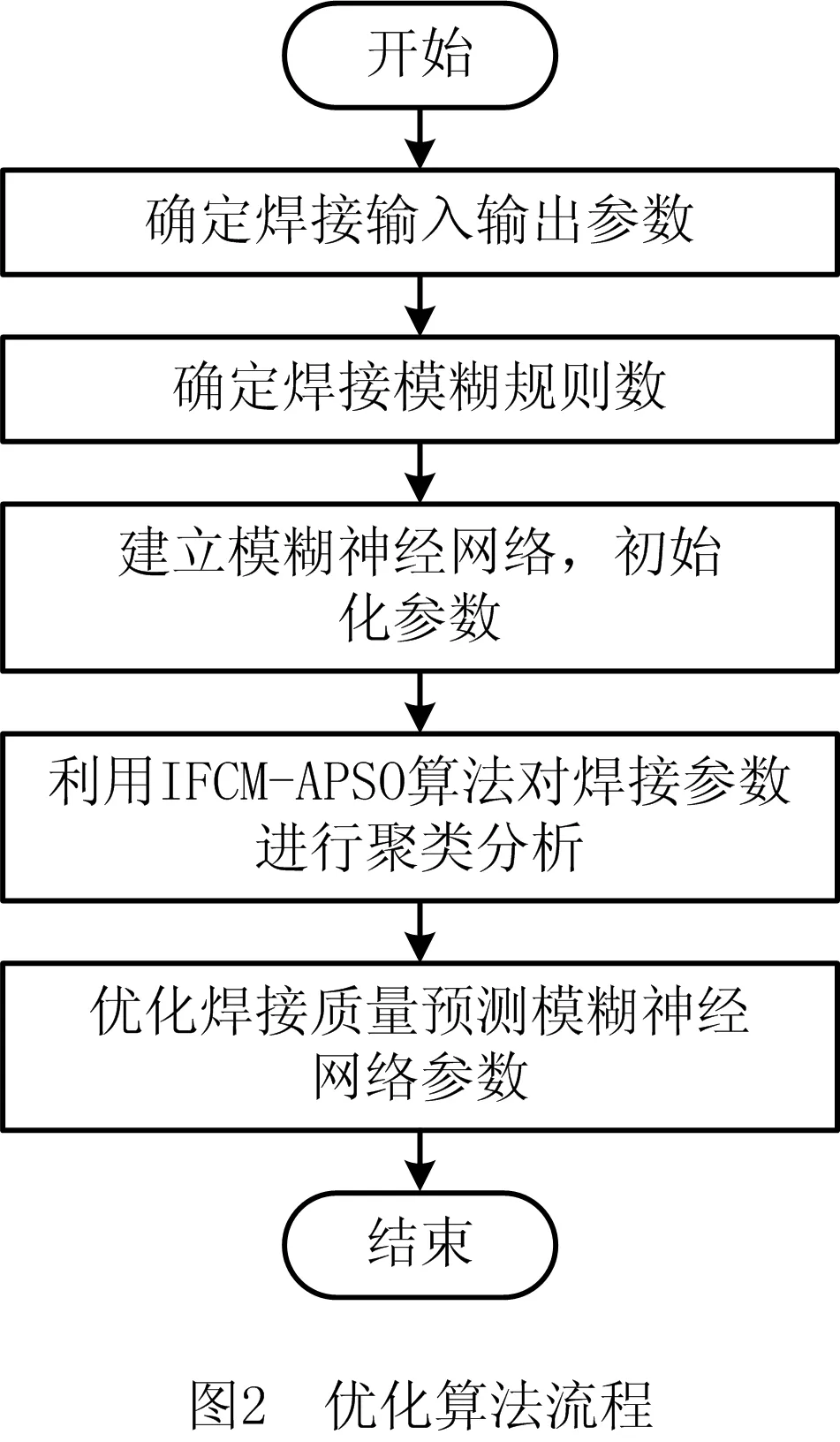
本文所提出的改进算法，首先根据输入的焊接参数数量和输出参数确定焊接模糊规则，完成初始化模糊神经网络的建立；接着利用IFCM-APSO算法对输入焊接参数空间进行初始化，将焊接参数空间分解为n个焊接模糊子空间，同时确定焊接参数模糊子空间的聚类中心c，计算焊接隶属函数的宽度b；最后利用得到的优化参数对初始模糊神经网络进行迭代更新，最终得到用于焊缝外形预测的模糊神经网络结构。具体流程如图2所示。

3 仿真与实验验证

3.1 焊接机器人实验平台的构成

机器人焊接系统主要由激光器、吹气口、送丝机、机械臂、机器人控制柜、线激光传感器等部分组成，如图3所示。激光器采用锐科系列的连续光纤激光器，如图4所示，最高功率可达6 000 W，相较于传统激光器，具有更高的光电转换效率，更低的功耗和更好的光束质量。由于其柔性的激光输出方式，能够方便地与系统设备进行集成。机器人采用KUKA六自由度焊接机器人，在焊接过程中采用氩气作为保护气体，可以提高焊接质量，降低焊接总体成本，提高焊接效率。

以保护气体流量、焊接速率、送丝速率和激光功率作为模糊神经网络的4个输入参数，分别以焊宽和焊高作为网络输出。保护气体流量太大时，气体冲击熔池，使熔池飞溅增加，焊缝表面不光滑；保护气体流量过小时，降低了对熔池的保护作用，并且容易产生气孔等缺陷。焊接速率过快时，气体保护作用受到破坏，使焊缝成形不好；当焊接速率过慢时，熔宽过大，熔池变大，容易将材料焊穿。送丝速率过快则会增加焊缝的焊宽和焊高；过慢则容易造成虚焊，影响焊接材料的力学性能。激光功率的选择对焊缝成形也有很大的影响，功率过大熔深增加较快，焊宽和焊高也相应有所增加。

上述输出参数是通过线激光传感器获取的，如图5所示。线激光传感器利用高精度摄像头，通过三角测距法获取焊缝的焊宽和焊高，采集到的焊缝截面图像如图6所示。

3.2 仿真与实验验证

模糊神经网络的准确性和适用性很大程度上取决于可用的训练数据集，数据集越大，其覆盖的输入范围就越大，生成的网络就越好。本文对3 mm厚的钛合金壁板进行了焊接试验，通过改变工艺参数，生成250个数据集。随机选择其中200个用于模糊神经网络的训练，其余50个用于测试网络的拟合程度；建立了两个独立的模糊神经网络模型，分别用于焊宽和焊高数据的预测。如图7所示为典型T型焊缝的形状参数。

模糊神经网络根据训练样本的输入、输出维数确定输入节点个数为4，输出节点个数为1，根据网络输入输出的节点个数，人为确定隶属度函数个数为8，因此构建的网络结构为4-8-1，网络结构如图8所示。

第一层为输入层，各个节点直接与焊接参数相连接，该层节点数为焊接输入参数的个数4；第二层为隶属度计算层，即将输入的焊接参数模糊化，隶属函数选择高斯型隶属函数进行计算；第三层为模糊规则匹配层，每一个节点代表一条模糊规则的匹配；第四层为归一化层，节点数与第三层相同；第五层为输出层，对计算结果进行清晰化处理。

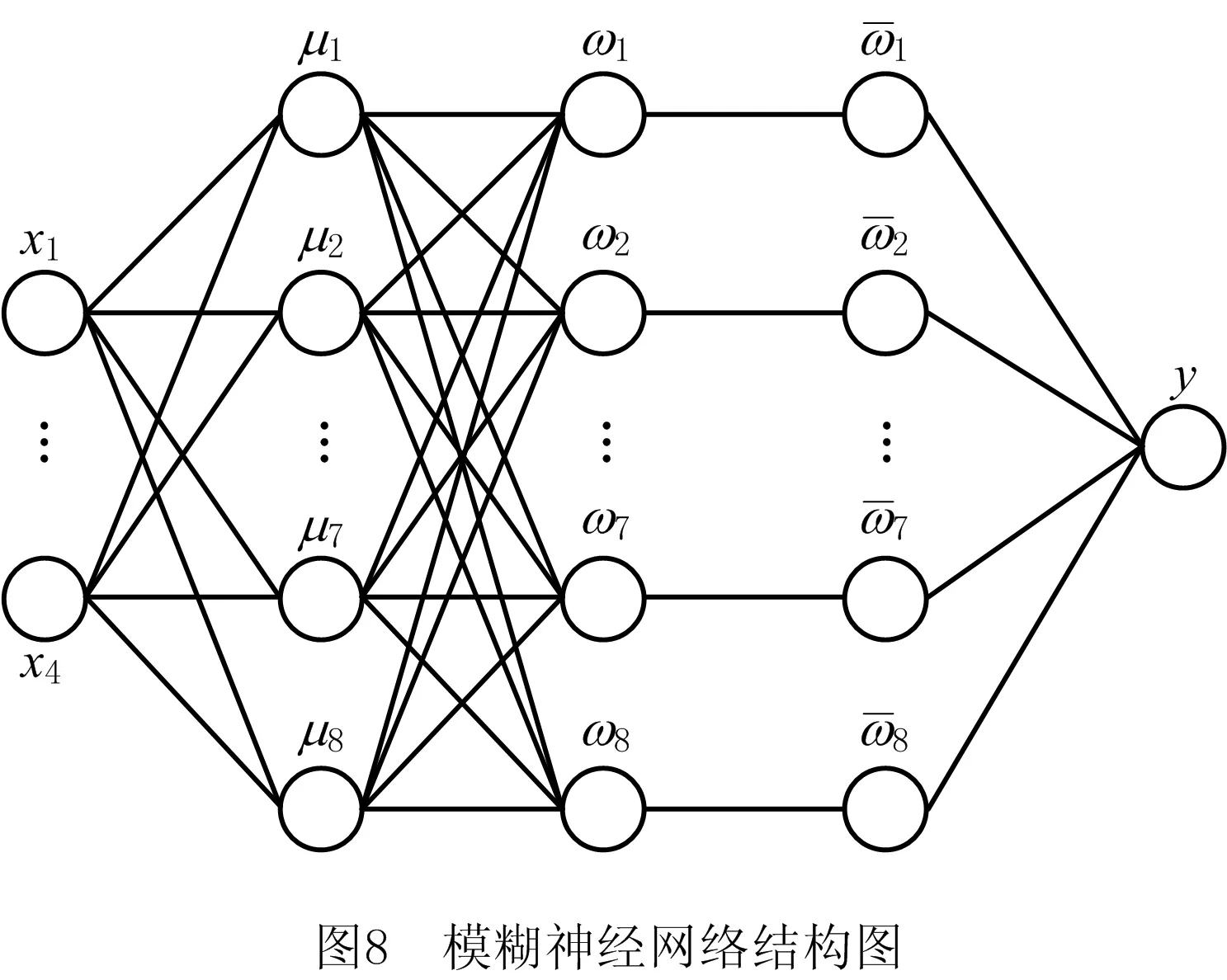
图8 模糊神经网络结构图在实际应用过程中，焊接参数的范围如表1所示。

表1 焊接参数范围

为了更好地确定隶属函数的中心值和宽度，在MATLAB 2019b中采用IFCM-APSO算法编写程序对前件参数进行优化，并对优化后的模糊神经网络进行数据测试，优化前后的误差变化如图9和图10所示。

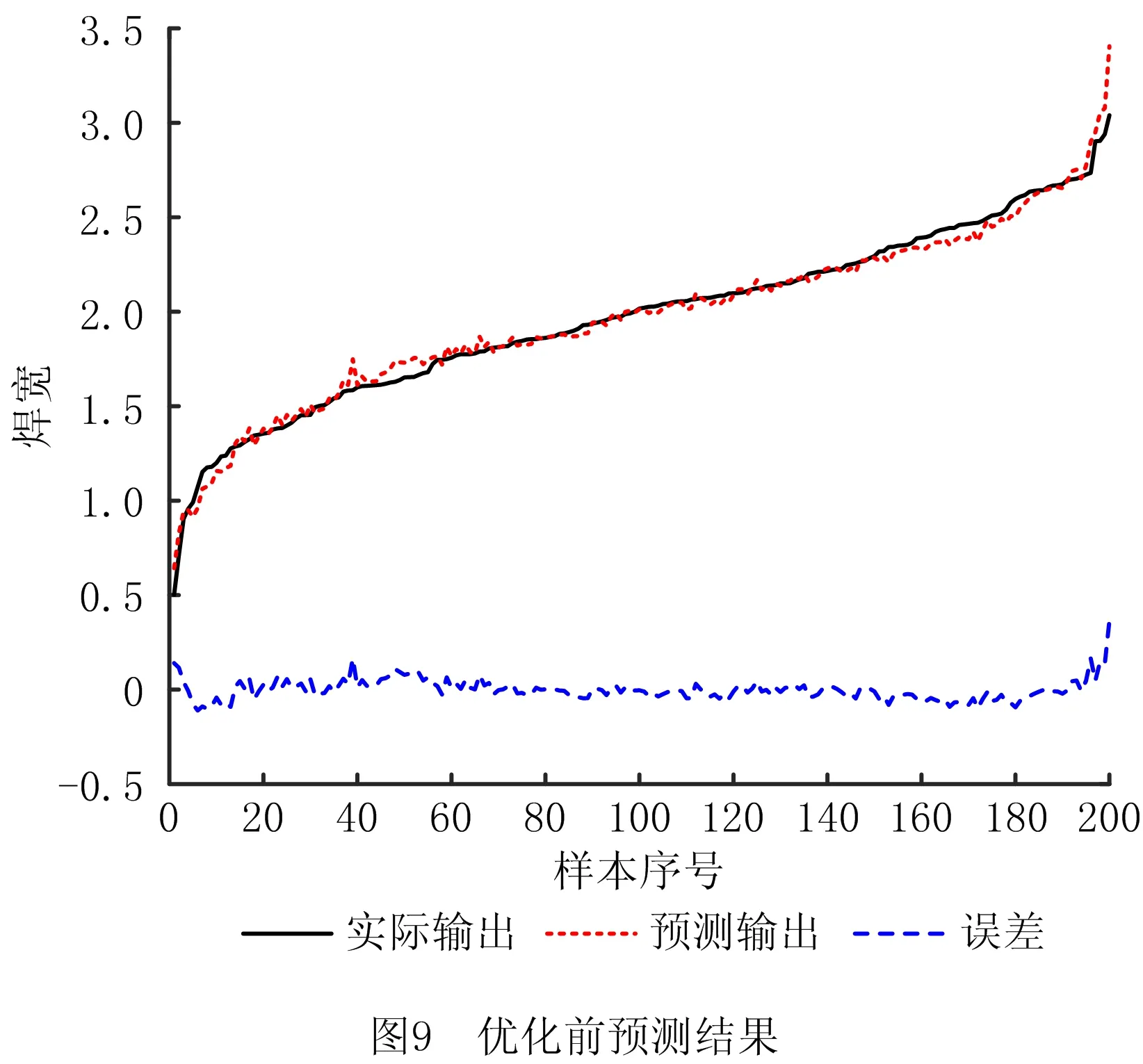
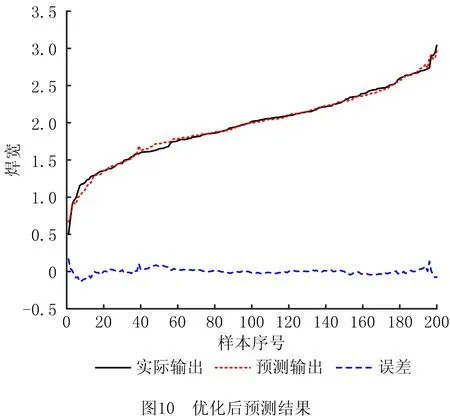
由图9可以看出，与实际输出相比，预测输出数据波动较大；由图10可以看到，将前件参数利用IFCM-APSO算法优化之后，提高了模糊神经网络拟合程度。

此外，将优化后的模糊神经网络预测模型与传统BP神经网络进行对比，BP神经网络预测结果如图11所示。

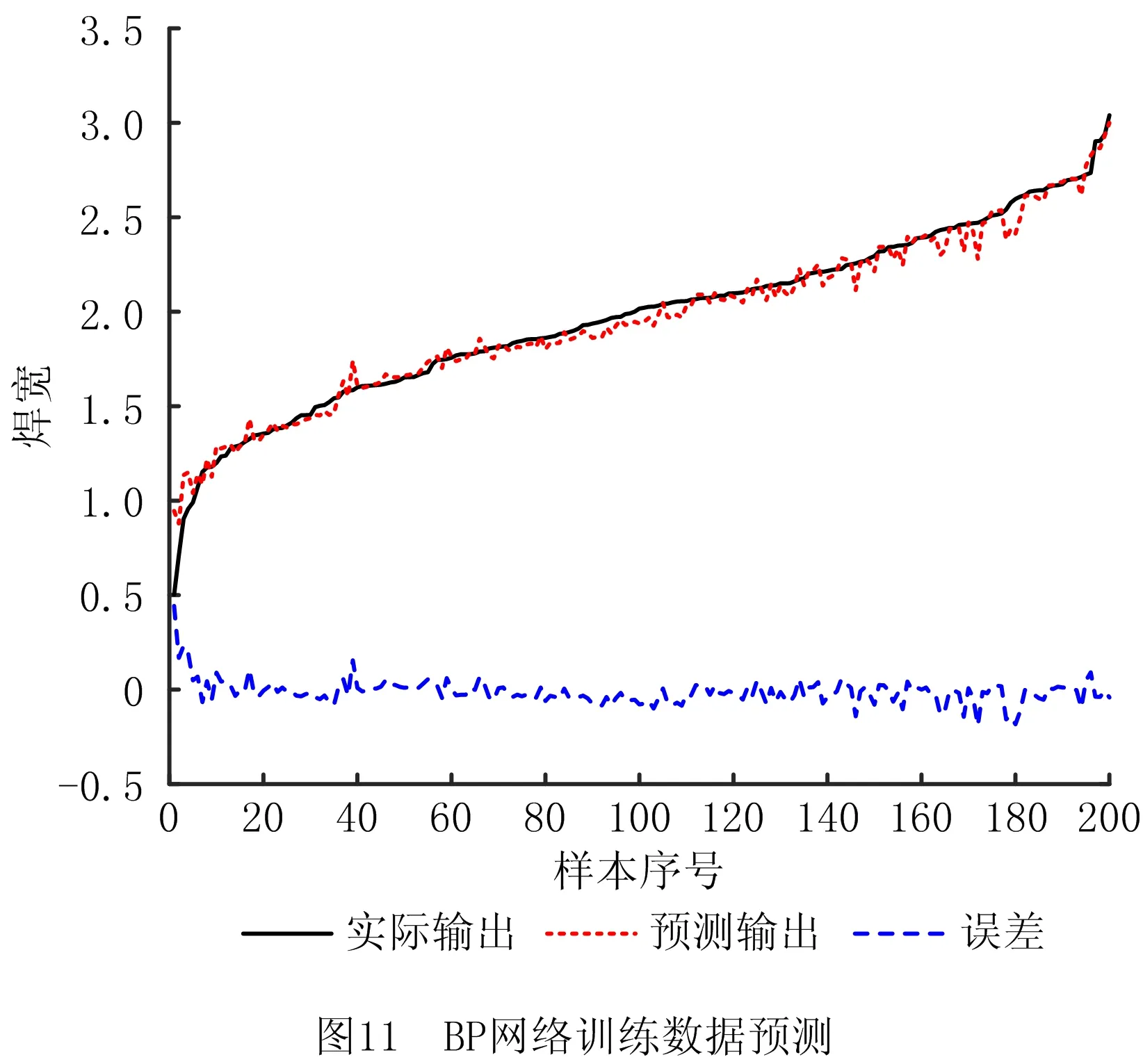
通过比较改进后的模糊神经网络和BP神经网络在运算时间、误差等方面的数据，发现优化后的模糊神经网络在运算速度和预测准确率上优于BP神经网络。对比结果如表2所示。

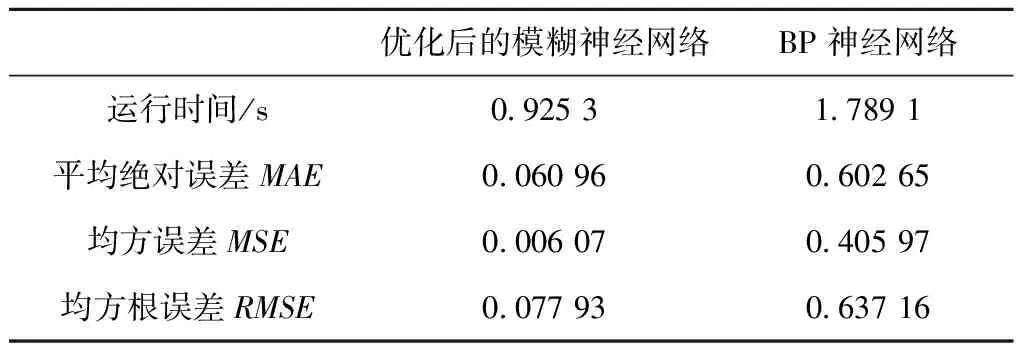
表2 网络数据对比

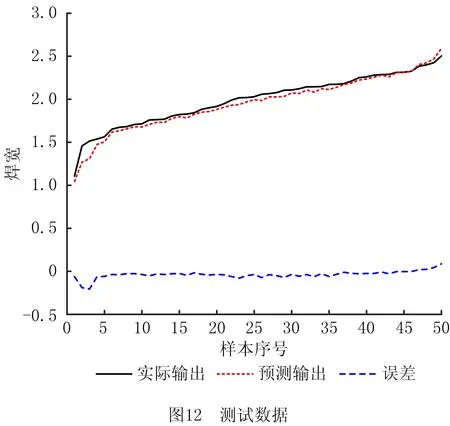
将测试数据集代入优化后的模糊神经网络可得图12，图12结果表明改进算法对减小误差的有效性。

在实际工程中，本文选择了25组焊接参数，并对其焊接结果利用改进后的模糊神经网络进行预测，预测结果如图13所示。

图14为采用人工试焊方法，经过5次参数调整后得到的焊接结果，可以看出，焊缝表面粗糙不均匀，在有限次调整次数范围内，难以达到预期的焊接效果；图15为利用改进后的模糊神经网络在焊接前根据预测结果，经过3次焊接参数调整所得到的焊缝成型图。焊接效果图表明，所用改进后的模糊神经网络可以对焊缝外形尺寸作出一定误差范围内的预测，有效提高了焊接参数的调整效率。

4 结束语

本文面向焊接机器人的焊缝外形尺寸预测，提出一种基于直觉模糊C均值聚类和自适应惯性权重粒子群算法(IFCM-APSO)相融合的改进自适应模糊神经网络控制方法，采用高斯函数作为隶属度函数，利用IFCM-APSO算法对高斯函数的中心值和宽度进行寻优计算。本文以T型焊缝的焊脚宽度和焊高高度作为网络预测输出结果，选择焊接速率、激光功率、送丝速率和保护气体流量这4种变量作为输入参数，对自适应神经网络模糊推理算法中隶属函数的中心值和宽度进行优化。仿真和实验结果表明，本文所提出的机器人焊接焊缝外形预测方法，较好地对输入输出参数进行非线性拟合，其预测值与实际值的误差在0.2 mm范围之内，为实际焊接过程中，焊接参数的选择提供了可靠的参考依据。但是，在焊接过程中影响焊接质量的因素有很多，本文只选取了4个参数作为研究对象，同时，各参数的变化对焊接质量的影响效果仍需大量实验结果进行分析。由于实验设备和实验成本限制，还可以考虑进行更多焊接实验，获取更多数据来训练模型，使模型预测更加准确。