基于近邻转移约束规则的非确定工业过渡过程的模态识别方法

朱明睿，纪杨建，甘红宇，张 念

(浙江大学 机械工程学院浙江省先进制造技术重点研究实验室，浙江 杭州 310027)

0 引言

受生产计划调整、产品指标变动、材料成分波动等不确定因素的干扰，工业生产系统容易偏离当前的稳定工况，出现大范围非平稳情况，系统重新恢复至稳定工况的过程称为过渡过程。一个完整的过渡过程往往包含多次过渡模态转换，而当前调控人员仅依靠经验难以识别不同过渡模态，导致调控可靠性低，系统恢复稳定耗时长，因此及时准确地识别过渡模态对于有效监测生产、优化调控决策，以及快速恢复系统稳定非常重要[1]。

为提高非确定工业过渡过程的模态识别效果，现有研究主要分为基于距离的过渡模态识别和基于模态关系的过渡模态识别。

基于距离的过渡模态识别是通过构建模态指示变量或度量指标，进行过渡模态划分和识别。一些学者从变量统计特征、数据密度信息[2-3]、数据概率分布[4]等角度构建了用于表征具有复杂数据分布的过渡模态指示变量，将过渡过程划分为多个子时段或子模态。例如，张淑美等[5]提取了非稳定工况的均值向量作为聚类算法输入，将隶属于同一簇的连续工况合并为一个子时段。HE等[6-7]从变量相关结构和关系的角度出发，提出了分布式模型投影、互信息相似性分析等方法，基于样本对模型适应性、观测值的自相关性以及不同潜变量之间的相似性，构建了数据块相似性的度量指标，得到包含多个子模态的过渡过程。还有学者在距离度量的基础上考虑了过渡过程的时序特性，按时间方向以顺序方式识别模态[8]。REN等[9]构建了最大均值差异指标刻画窗口工况的局部数据概率分布，引入大长度窗口检测到过渡过程后，利用小长度窗口细分出过渡子模态。

基于模态关系的过渡模态识别是通过提取稳定模态与过渡模态的关系，依据变化趋势进行过渡模态识别。部分研究检测了过渡过程的起始时间段[10-11]，但并未针对过渡过程中的模态特性做进一步研究。SRINIVASAN等[12-14]指出受工艺过程的固有特性和物理约束影响，系统在特定调控方案下倾向于服从一定的过渡轨迹，过渡规律是有迹可循的，模态间存在依赖关系。基于该思想，ZHAO等[15]、PENG等[16]、CHEN等[17]将过渡过程描述为相邻稳定模态加权组成的变化过程，通过构建相邻稳定模态模型的加权指标识别过渡模态。SONG等[18]设置了参考模态数据集，根据密度信息判断待识别工况数据与参考稳定模态之间的差异，识别过渡过程的多个过渡子模态。GAO等[19-20]利用偏最小二乘(Partial Least Squares，PLS)算法捕获了过渡过程和相邻模态的共同特征，联合过渡过程的局部信息构建了两个过渡模态候选识别模型，通过在线过程中候选模型的被选择结果，揭示了过渡模态过程特性沿时间方向的动态渐变趋势。

非确定工业过渡过程由于偏离稳定工况的原因复杂，在设备高度耦合的情况下，变量关系、动态时变特性、非线性特性相比稳定工况更加复杂[21]，形成的过渡模态特性和样本分布各异[22]，并且由于工业过程固有特性，过渡模态之间并非完全独立，部分模态倾向于转换到变量取值相近的模态，部分模态则由于物理关系或操作参数限制无法互相转换或只能单向转换。而现有的基于距离和模态关系的过渡模态识别研究方法多是建立在工况数据局部符合高斯分布、局部保持线性结构、样本分布均匀紧密或过渡模态独立分布的假设下，对于具有明显的非线性数据特性，且过渡模态自身存在动态渐变和依赖关系的非确定工业过渡过程并不适用[23]。

因此，本文提出基于近邻转移约束规则的过渡模态识别方法。首先构建历史稳定工况核主成分分析(Kernel Principle Component Analysis, KPCA)模型，筛选关键过程变量并计算变量贡献作为模态聚类的距离度量，将历史工况划分为多个稳定模态簇和过渡模态簇。将KPCA模型统计量控制限用作稳定工况监测阈值，实时判断系统是否进入过渡过程。然后考虑了模态数据分布特性和模态转移的依赖性，结合近邻思想和模态转移约束思想，建立了近邻转移约束规则，对过渡过程工况进行过渡模态的两步识别：第一步引入移动窗口，计算待识别窗口工况的近邻贡献距离，与各过渡模态簇的近邻贡献距离阈值对比，匹配候选过渡模态集；第二步计算历史非稳定工况的过渡模态转移概率矩阵作为权值矩阵，对待识别窗口工况在各候选过渡模态簇中的近邻贡献距离进行加权和比较，最终确定待识别窗口工况的所属过渡模态。最后采用矿渣粉磨系统验证了所提方法的有效性。

1 近邻转移约束规则下的变量贡献距离

(1)变量贡献

变量贡献作为衡量过程变量对工况信息贡献程度和重要程度，以及受异常工况影响程度的指标，能够压缩表示原始数据的主要信息。过渡过程中，变量间的相关性会偏离正常的相关结构，受异常工况影响显著的变量贡献也会出现较大变化，因此变量贡献非常适合用于建模模态内部特性，作为模态聚类时的相似性度量指标。

变量贡献的计算包含两部分：①计算过程变量对包含了主要工况变化信息的主成分空间的贡献程度;②计算过程变量对包含了残余的工况变化信息的残差空间的贡献程度。考虑到工况数据的非线性，本文构建了KPCA模型[24]。KPCA模型是在PCA的基础上结合核方法的思想，将非线性数据映射至高维空间中进行非线性特征提取和数据分离。其中，KPCA模型的统计量Hotelling-T2衡量了经映射后，高维特征空间内核主成分模型内部的波动情况，统计量SPE衡量了某时刻输入的测量值偏离核主成分模型的距离。因此基于KPCA模型的变量贡献计算方法如下：

假设标准化原始工况数据集为x=(x1,x2,…,xn)∈J(n=1,2,…,N)，经非线性映射至高维特征空间后，得到数据集∅(x)=(∅(x1),∅(x2),…,∅(xn))∈H。

在特征空间中∅(x)的协方差矩阵表示为：

(1)

ΣF的特征向量ν作为高维空间的投影方向，存在系数an(n=1,2,…,N)使其线性表示为：

(2)

为了求解特征向量ν，定义核矩阵K∈N×N，利用核函数Kij=〈∅(xi),∅(xj)〉(i,j=1,2,…,N)代替非线性函数∅(·)在高维特征空间中的内积。核函数的选取对于考量输入参数的非线性相关性对统计量T2和SPE求解的影响非常关键，本文选择应用最为广泛、性能表现佳的高斯径向基核函数，能够方便地求解核矩阵K的特征值λ和特征向量a=[a1,a2,…,aN]T，并进一步求解特征向量ν：

Nλa=Ka。

(3)

获取映射数据∅(x)在特征向量νa上的投影，即非线性主成分得分：

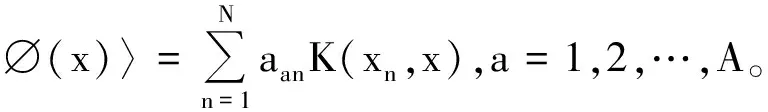
(4)

进一步计算统计量T2，如式(5)所示：

T2=[t1,t2,…,tA]Λ-1[t1,t2,…,tA]T。

(5)

其中：A为保留的核主成分个数，Λ为与主成分得分向量对应的协方差矩阵。

进一步计算统计量SPE，如式(6)所示：

(6)

式中：N代表模型中样本个数，A为保留的核主成分个数，ti代表映射数据∅(x)的第i个主成分的得分。

对于样本向量xnew，则xnew的第i个变量对T2和SPE的贡献分别为：

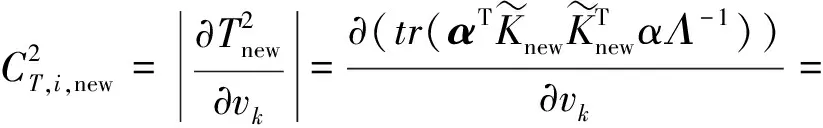
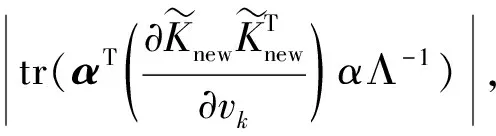
(7)

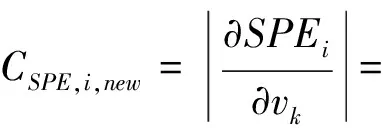
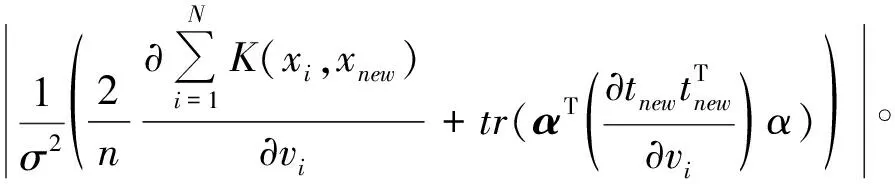
(8)

得到xnew的变量贡献向量，记为

(2)近邻转移约束规则

近邻转移约束规则反映了一个样本基于模态转移先验知识，与其在特定模态内的最近邻的数个样本之间的相似性，用于从数据集中挖掘出样本与模态之间的相似关系。

“近邻”表现为K近邻思想，即从整个数据集中找到每个样本的k个最相似(特征空间中最近邻)样本。K近邻方法健壮性强，在工业过程监测中常用于指导提取正常样本的最近邻距离特征量[25-27]，在K近邻思想下度量样本与模态相似性，能够提升过渡模态类型匹配的鲁棒性。

“转移约束”表现为过渡模态转移概率，一个过渡模态转移到另一个过渡模态的概率越接近于1，表明模态间转移趋势越强；概率越接近于0，表明模态间转移可能性越小。为了获取模态转移先验知识，对历史非稳定工况的过渡模态转移过程进行模态转移概率统计，构建过渡模态转移概率矩阵，矩阵对角元素表示过渡模态在下一时刻保持模态类型不变的概率，非对角元素表示过渡模态在下一时刻转移到其他过渡模态的概率。值得注意的是，由于过渡模态间的转移具有方向性，过渡模态转移概率不具备对称性，即两个过渡模态间的正向和反向的转移概率可能并不相等。

总之，近邻转移约束规则下的变量贡献距离，是以样本变量贡献作为距离度量指标，以特定过渡模态间的转移概率作为权值系数，获取一个样本与其在特定过渡模态内的k个最近邻样本之间的变量贡献距离加权的结果。

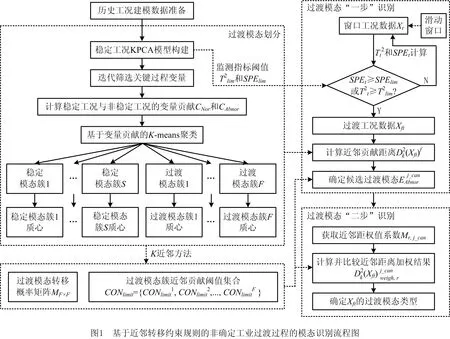
本文通过计算近邻转移约束规则下的变量贡献距离，进行过渡模态划分和过渡模态识别，如图1所示为基于近邻转移约束规则的非确定工业过渡过程的模态识别流程图。

2 基于变量贡献的过渡模态划分

首先构建了历史稳定工况KPCA模型，获取各关键过程变量的变量贡献，用于筛选关键过程变量，在此基础上，将关键过程变量贡献数据作为K-means算法输入进行过渡模态划分。

(1)关键过程变量筛选

将历史稳定工况数据XNor划分为训练集和测试集，每次随机选取90%的训练集训练KPCA模型，基于式(5)～式(8)计算变量贡献，并根据累计贡献准则，筛选训练集最关键的q个过程变量。基于训练得到的KPCA模型计算测试集变量贡献，筛选测试集最关键的q个过程变量。比较训练集和测试集筛选结果，若相似度超过90%，则确定KPCA模型参数；否则重复上述训练和测试过程，直至筛选结果相似度超过90%。

(2)工况序列样本的变量贡献

对历史稳定工况数据XNor和历史非稳定工况数据XAbnor均以长度l进行序列分割，获得历史稳定工况序列样本集XNor_seq={XNor,1,XNor,2,…,XNor,M}和历史非稳定工况序列样本集XAbnor_seq={XAbnor,1,XAbnor,2,…,XAbnor,N}，M和N分别是单个稳定工况序列和单个非稳定工况序列的个数。其中单个稳定工况和单个非稳定工况序列分别记为XNor,m∈Rl×p(m=1,2,…,M)和XAbnor,n∈Rl×p(n=1,2,…,N)，p是过程变量个数。

基于式(7)和式(8)计算单个稳定工况序列XNor,m的变量贡献，记为CONNor,m：

CONNor,m=[cT2,1,Nor,m,cT2,2,Nor,m,…,

cT2,p,Nor,m,cSPE,1,Nor,m,

cSPE,2,Nor,m,…,cSPE,p,Nor,m],

m=1,…,M。

(9)

其中cT2,p,Nor,m和cSPE,p,Nor,m分别表示XNor,m的第p个过程变量对T2和SPE的贡献。

获得XNor对应的历史稳定工况变量贡献数据，记为CONNor：

CONNor=[CONNor,1,CONNor,2,…,CONNor,M]。

(10)

(3)过渡模态聚类

假设历史工况数据包含S种稳定模态和F种过渡模态。

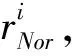
(11)

对S个稳定模态簇分别构建KPCA模型。

对于单个非稳定工况序列XAbnor,n，基于该序列初始稳定模态的KPCA模型，计算变量贡献，记为CONAbnor,n：

CONAbnor,n=[cT2,1,Abnor,n,cT2,2,Abnor,n,…,cT2,p,Abnor,n,

cSPE,1,Abnor,n,cSPE,2,Abnor,n,…,cSPE,p,Abnor,n],n=1,…,N。

(12)

其中cT2,p,Abnor,n和cSPE,p,Abnor,n分别表示XAbnor,n的第p个过程变量对T2和SPE的贡献。

获得XAbnor对应的历史非稳定工况变量贡献数据，记为CONAbnor：

CONAbnor=[CONAbnor,1,CONAbnor,2,…,CONAbnor,N]。

(13)

对于所属模态簇未知的工况向量Xsample，其变量贡献向量为CONsample，其中：

CONsample=[cT2,1,sample,cT2,2,sample,…,cT2,p,sample,

cSPE,1,sample,cSPE,2,sample,…,cSPE,p,sample]。

(14)

则Xsample到稳定模态簇ENori质心的变量贡献距离：

(15)

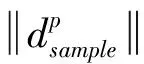
3 基于近邻转移约束规则的过渡模态识别

3.1 过渡模态的“一步”识别

假设存在模态Ef，其工况数据集为Xf=[x1,x2,…,xn]T，变量贡献数据集为Cf=[c1,c2,…,cn]T。则样本xi在模态Ef中的k个最近邻样本集，记为KNN(xi)f：

KNN(xi)f={xj∈Xf|d(ci,cj)≤d(ci,NNk(ci))}。

(16)

其中:d(ci,cj)是xi的变量贡献ci和xj的变量贡献cj之间的欧式距离，NNk(ci)是ci的第k个近邻点。

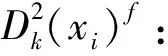
(17)

在在线过程中，将历史稳定工况KPCA模型的统计量控制限用作稳定工况监测阈值，将各过渡模态簇的近邻贡献距离阈值作为候选过渡模态集筛选阈值。引入移动窗口，实时判断移动窗口工况是否进入了过渡过程。

值得注意的是，在窗口移动步长Δt的选取上，一方面需要保证移动后的窗口数据能够捕获到更新的数据信息，避免步长过小导致相邻窗口工况数据重复过多，信息冗余的问题。另一方面又需要避免步长过大跨越多个过渡模态，导致工况数据信息被遗漏的问题。滑动窗口思想在诸多论文中都有相关应用，其中TAN等[28]在论文中给出了一些经验性取值，即稳定模态的窗口长度一般取“最小稳定模态长度”，即稳定模态持续的最短时间，而窗口的移动步长则按照小于最短稳定模态持续时间的二分之一取值，或者以过程变量数量的2～3倍取值，但在实际应用中，需要根据工业生产的过程特性，通过对数据的反复实验来确定窗口移动步长的最终取值。

下面是过渡模态的“一步”识别的过程：

(1)在当前时刻t，引入长度为l，移动步长为Δt的移动窗口。

(2)对于实时移动窗口数据Xt∈Rl×p，计算统计量T2t和SPEt。

(3)将SPEt和T2t与历史稳定工况KPCA模型的统计量控制限SPElim和T2t比较，若连续l/2个时刻的统计量超过控制限，即SPEt≥SPElim或T2t≥T2lim，则当前时刻窗口工况非稳定，进入过渡过程，此时将窗口工况Xt描述为过渡工况Xft，依据式(7)和式(8)计算Xft的变量贡献CONft，CONft=[cT2,1,ft,cT2,2,ft,…,cT2,p,ft,cSPE,1,ft,cSPE,2,ft,…,cSPE,p,ft]；反之，表示当前时刻系统处于稳定状态。

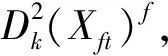
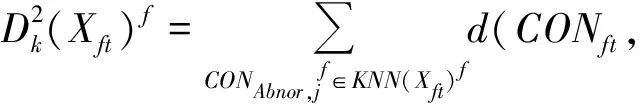
CONAbnor,jf)2,f=1,2,…,F。

(18)

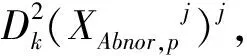
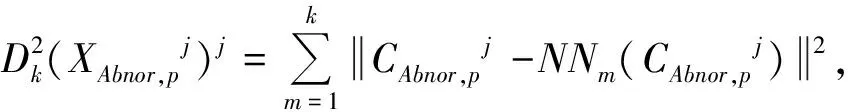
j=1,2,…,F；

(19)

CONlimit={CONlimit1,CONlimit2,…,CONlimitF}。

(20)

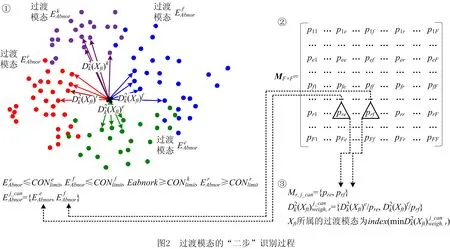
3.2 过渡模态的“二步”识别

采用特定过渡模态间的转移概率矩阵作为权值矩阵，对候选过渡模态的变量贡献距离进行距离加权，获得最小的距离加权结果所对应的过渡模态作为窗口工况所属的过渡模态。

假设每种过渡模态具有F-1个转向，系统由t时刻的过渡模态EAbnore，在t+1时刻转移到过渡模态EAbnorf的概率记为Pef(见式(21))。若Pef=0，表示过渡模态EAbnore无法直接切换至过渡模态EAbnorf；若Pef=1，表示过渡模态EAbnore一定会切换至过渡模态EAbnorf。

Pef=P{xt+1=EAbnorf|xt=EAbnore}，e,f=1,2,…,F。

(21)

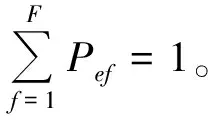
将F种过渡模态的转移过程描述为过渡模态转移概率矩阵MF×F:

(22)

(23)

过渡模态的“二步”识别过程如图2所示。

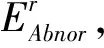
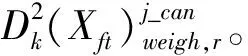
4 案例研究

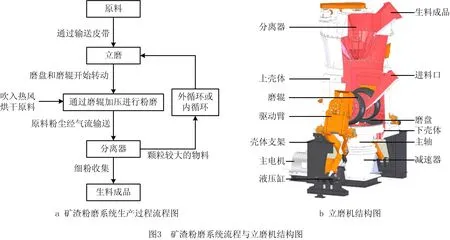
矿渣粉磨系统是一种广泛应用于水泥、钢铁、化工、冶金等行业的复杂高能耗非线性系统。系统集破碎、干燥、粉磨和分级输送于一体，可将块状和颗粒状原料磨成所需的粉状物料成品，作为水泥、陶瓷等产品的原料。实际生产中，受原料质量、燃气热值和环境温湿度等因素干扰，过程参数频繁波动，系统运行极不稳定，系统存在多种操作条件和运行工况。

矿渣粉磨系统主要由立磨主机、主排风机、热风炉、除尘器、斗提机、管带机等设备组成。物料在磨辊和磨盘之间被碾磨成粉状。碾磨压力除了磨辊自重外，主要主电机驱动磨辊对磨盘物料加压。经碾磨后的物料中存在大量粗粉，经选粉机气流分选后，大部分粗粉在气流流动过程中自动落到磨盘上，被再次粉磨。其余符合产品粒度规格的细粉则被选出为成品，经收尘及输送系统送入成品储库，其生产过程流程图如图3所示。

采集矿渣粉磨系统正常进料范围下的历史稳定工况和非稳定工况数据(采样间隔为2 s)，并将历史稳定工况数据划分为训练集和测试集。根据变量贡献排序进行关键过程变量筛选，获得的17个关键过程变量如表1所示。

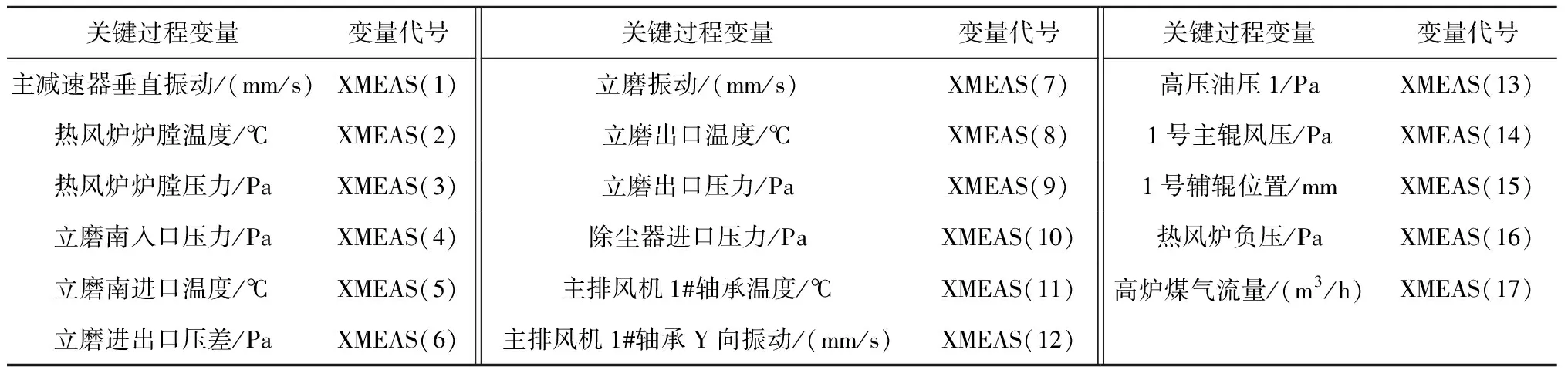
表1 矿渣粉磨系统关键过程变量

根据矿渣粉磨系统的实际生产特性，系统稳定工况的持续时间最短为2 min。因此,本文在案例研究中将窗口分割长度取值2 min，通过反复实验确定移动步长为16 s是最合理的。对分割后的正常工况序列样本集和非稳定工况序列样本集分别进行K-means聚类，根据肘部法则确定稳定模态簇数为6，过渡模态簇数为5。

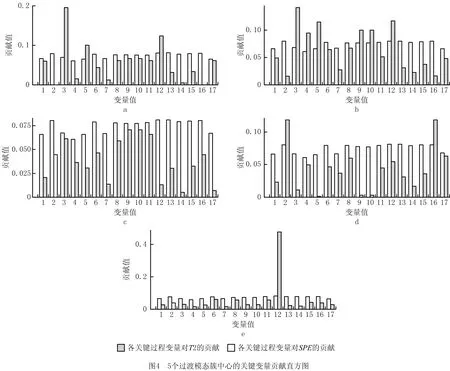
图4展示了5个过渡模态簇的质心各变量对统计量的贡献。由图4可以看出，尽管各过渡模态簇的变量贡献值不相同，但值分布存在相似之处，例如簇2(如图4b)和簇3(如图4c)中，变量3～5的变量贡献均形成小高峰，变量8～11的变量贡献再次形成小高峰。各过渡模态簇中，簇5(如图4e)最易识别，并且变量12的变量贡献远大于其他变量。

基于历史非稳定工况样本，得到的过渡模态转移概率矩阵如表2所示，对角元素表示各过渡模态不发生类型变化的概率，非对角元素表示不同过渡模态间的转移概率，可见对于矿渣粉磨系统而言，各过渡模态间均存在转移可能，拥有最大转移概率的是过渡模态3向过渡模态4的转移，拥有最小转移概率的是过渡模态3向过渡模态1的转移。

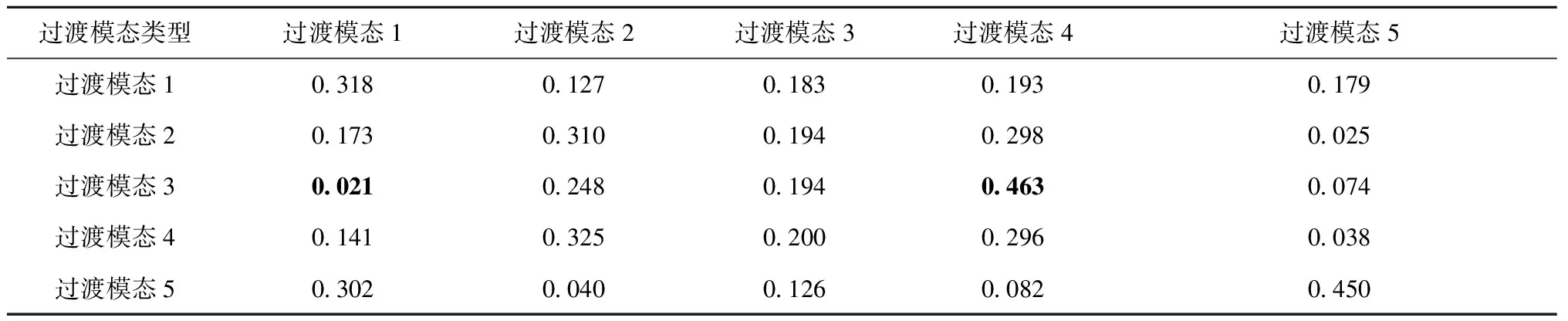
表2 过渡模态转移概率矩阵

选取一组包含完整过渡过程的待测试非稳定工况的过程数据，共2 000个样本，包含3种稳定模态(稳定模态1、稳定模态2、稳定模态3)和3种过渡模态(过渡模态3、过渡模态4、过渡模态5)，用于验证近邻转移约束规则下的变量贡献距离分析在过渡模态识别方面的有效性。其中，待测试非稳定工况包含的各模态对应时段如表3所示，关键过程变量XMEAS(1)-XMEAS(17)变化如图5所示。

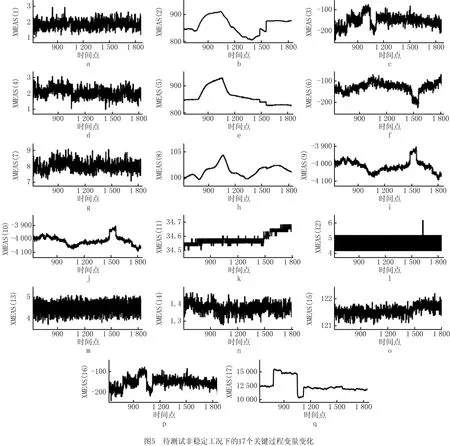
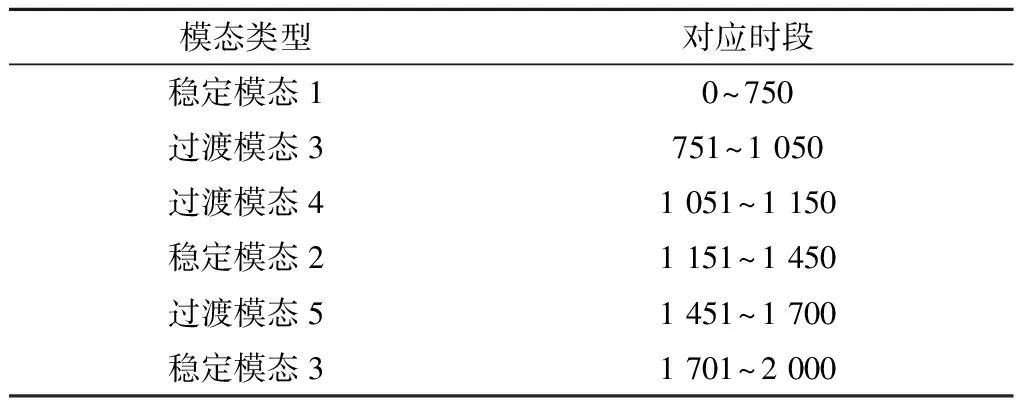
表3 待测试非稳定工况的各模态时间分布

图6展示了利用近邻转移约束规则的方法、基于近邻贡献的方法、基于密度聚类的方法和基于K-means聚类的方法，对待测试非稳定工况进行过渡模态识别的结果。基于近邻转移约束规则的方法的识别结果与图5中关键过程的变量变化情况一致，过渡模态间转移规律符合表2中的结果，模态识别结果没有出现识别噪声和错误识别的情况。基于近邻贡献的方法(如图6b)未考虑过渡模态转移，在第1 050个时间点，未成功地识别出过渡模态4，而是识别成过渡模态3到过渡模态1的转移，然而结合表2中过渡模态3到过渡模态1的转移概率为0.021可知，该方法的过渡模态识别结果与实际生产过程并不相符。基于密度聚类(如图6c)和基于K-means聚类(如图6d)的方法分别基于非稳定工况数据的密度分布和工况数据的欧式距离进行模态划分和识别，由于过渡过程数据噪声大、变量震荡幅度大，这两种方法的模态识别效果并不稳定，并且存在将过渡模态错误识别为稳定模态的情况。

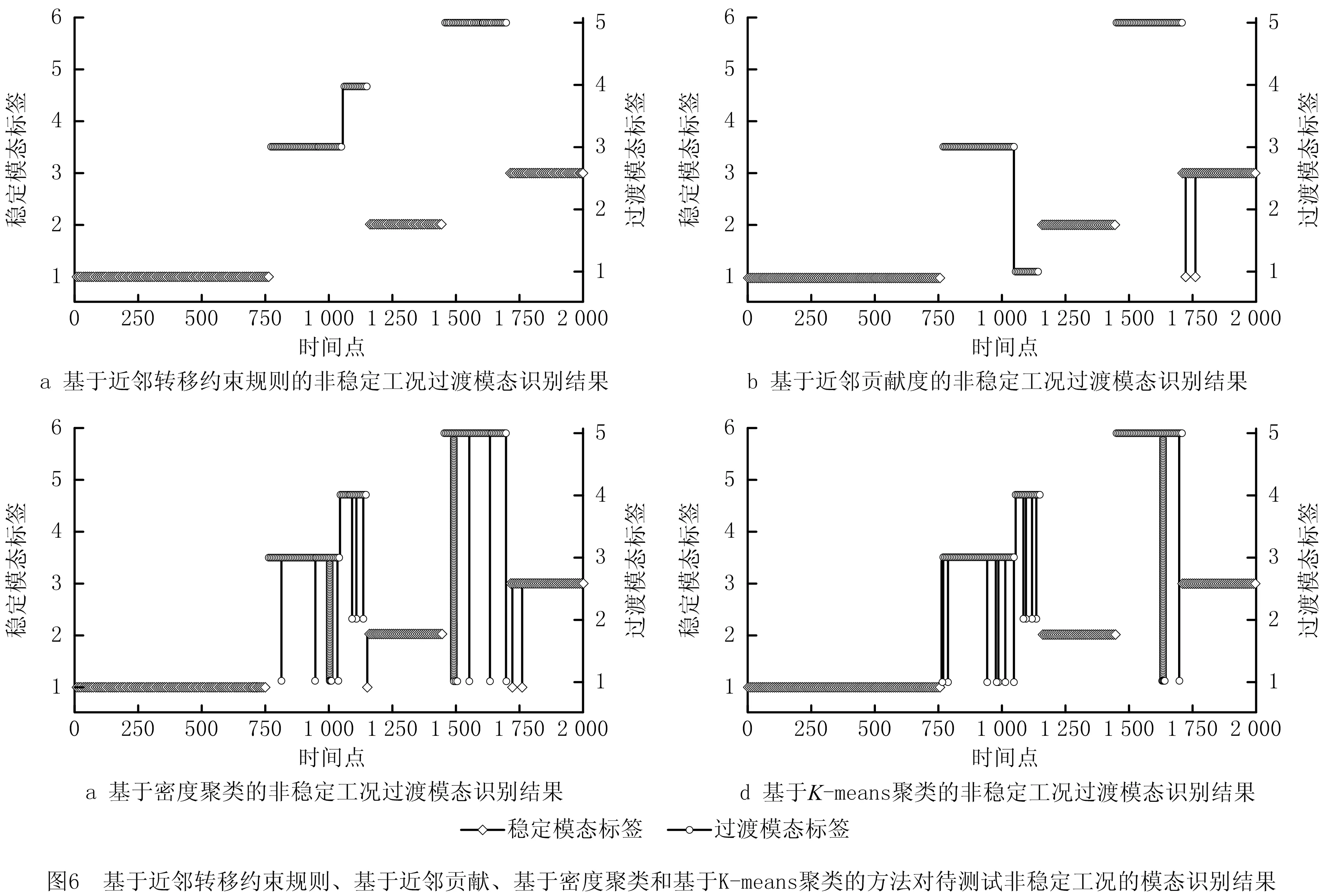
利用模态起始时刻识别误差、模态识别准确率指标定量分析不同模态识别方法结果，如表4所示。可见，基于近邻转移约束规则的方法在过渡模态起始时刻识别中，滞后时间短，过渡模态识别准确率最高，为98.10%；基于近邻贡献的方法识别准确率最低，为82.47%；基于K-means聚类的方法识别过渡模态起始时刻的误差最大。

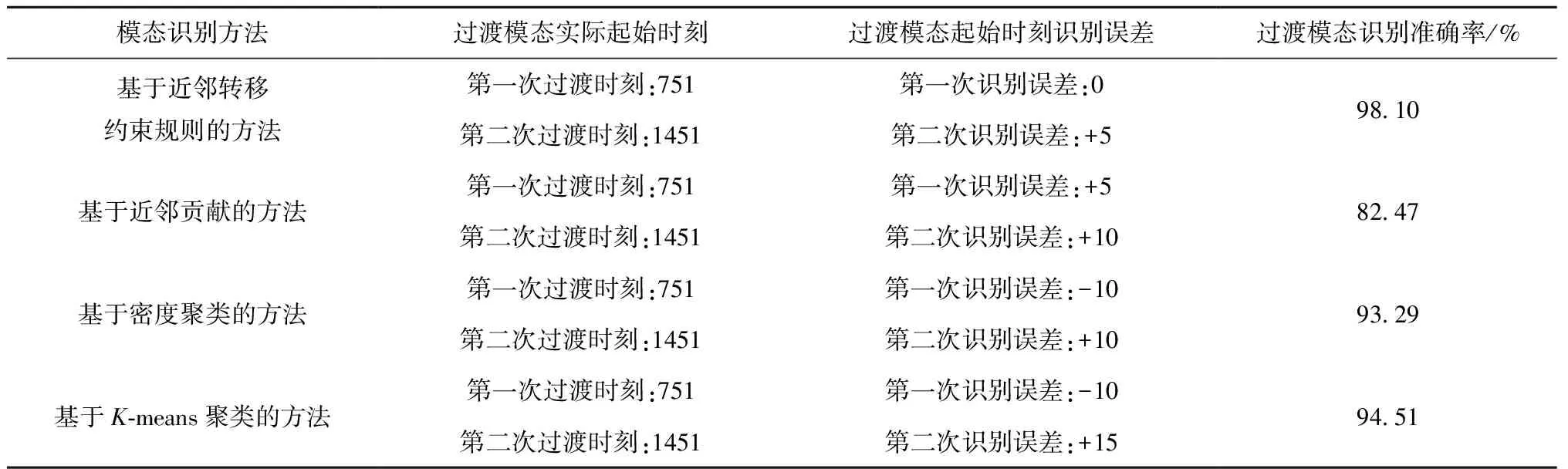
表4 待测试非稳定工况的模态识别结果对比

5 结束语

针对工业过渡过程的不确定性给过渡模态识别带来的挑战，本文提出一种基于近邻转移约束规则的过渡模态识别方法。该方法使用变量贡献作为模态聚类的距离度量指标，进行历史非稳定工况的过渡模态划分。为了解决过渡模态特性差异大、模态转换具有依赖性的问题，本文结合K近邻方法和模态转移的约束关系，建立了近邻转移约束规则，基于该规则进行两步识别，精确定位在线过程中待识别工况的过渡模态类型，最终通过矿渣粉磨系统的实际应用效果，证实了所提方法在非确定工业过渡过程模态识别中的有效性，有助于操作人员优化调控策略，帮助系统快速恢复稳定，在工程应用中有一定价值。

未来将在本文基础上重点探究多模态过程中根据变量贡献的变化自适应确定窗口长度的方法，并进一步考虑模态驻留时间和模态类型对模态识别的影响，从典型过渡过程出发，结合工艺过程机理，挖掘典型稳定模态和典型调控方案下的过渡规律，为操作人员优化调控方案提供有效依据。