硬涂层对镍基高温合金叶片的振动特性影响

党鹏飞, 于华涛, 杨铮鑫

(沈阳化工大学机械与动力工程学院， 沈阳 110142)

叶片是航天发动机的关键结构件之一，对发动机的正常运转以及安全性能有重大影响。为了保障叶片在高压、高温、高转速的极端环境下安全工作，通常在镍基高温合金叶片表面涂敷以陶瓷基、金属基以及陶瓷和金属混合形成的硬涂层，可以有效改善叶片抗冲刷和耐高温等性能，并提高叶片使用寿命。中外学者对于硬涂层叶片展开一些研究。刘蓉等[1]对单面局部涂敷硬涂层的悬臂板开展研究，优化了硬涂层在板面上的涂敷位置，并用试验证明了阻尼优化的有效性。杨光等[2]针对氧化铝涂层对涡轮叶片温度测量的影响，通过数值模拟对有无涂层的叶片进行瞬态热冲击，结果表明涂层对测量叶片的瞬态温度有显著影响。袁巍等[3]基于ANSYS模拟了带冠预扭涡轮叶片的振动，得出非线性接触预应力模态分析的方法比传统模态分析得到的结果更精确。张翼飞等[4]采用有限元研究了不同厚度的TiN/Ti涂层对钛合金叶片冲击塑性应变的影响，优化了涂层的结构设计参数。王娇等[5]用有限元法对金属基和陶瓷基两种涂层叶片进行研究,结果表明,两类硬涂层的厚度和涂覆位置都对叶片固有特性有明显影响。姚青文等[6]介绍了在某型燃机涡轮叶片制备的底层CoCrAlY厚度120 μm+陶瓷层厚度80 μm的热障涂层热腐蚀性能良好。Dang等[7]对非线性温度梯度下硬涂层叶片的振动特性开展研究，分析了横向激励下硬涂层叶片的响应特性。Yao等[8]研究了旋转叶片在强迫激励下的非线性振动和稳态响应，分析了阻尼和转速等因素对其的影响规律。Zhao等[9]研究了复合材料悬臂层合矩形板在超音速气流和面内激励作用下的非线性动力学特性，得到了频率响应曲线、相位图和频谱。Witek[10]通过开展仿真和试验研究了压气机叶片在共振条件下疲劳裂纹扩展的特性，获得了压气机叶片裂纹长度随载荷循环次数变化的曲线。

基于此，现开展考虑不同涂敷方式和厚度的硬涂层叶片动力学研究，分别建立无涂层、涂敷有不同厚度的单、双面硬涂层的镍基高温合金叶片有限元模型。采用ANSYS软件进行预应力模态分析与谐响应分析，利用坎贝尔图进行共振特性分析，分析硬涂层叶片的非线性振动特性。通过无涂层、涂敷有不同厚度的单、双面硬涂层振动特性的比较分析，获得硬涂层对叶片振动的影响规律。

1 硬涂层叶片模型建立

1.1 建模参数

叶片模型尺寸的叶高为304.75 mm，叶根宽为66.00 mm，弦长为142.50 mm，厚度为3.42 mm。叶片稳定工作运转角速度为230 rad/s。叶片基底选用镍基高温合金GH4169，涂层材料选用NiCoCrAlY+YSZ，相关材料参数如表1所示。

表1 叶片材料参数

1.2 单元选择和涂层类型

叶片有限元模型如图1所示，并分别在叶片的单面和双面形成大小形状与叶片相同、厚度不同的面作为涂层。在单元类型选取中，考虑到叶片的曲面和涂层结构，对叶片、叶身采用SOLID187单元进行网格划分，对叶片涂层采用SHELL181单元进行网格划分。在保证网格质量和精度的前提下，设置网格大小为2 mm，划分无涂层叶片网格节点和单元数量分别为176 378、93 965。考虑以0.05为梯度，分别在叶片上表面和双面涂敷厚度为0.10、0.15、0.20 mm的涂层。

图1 硬涂层叶片有限元模型Fig.1 FEM model of hard-coating blade

2 振动特性分析

2.1 分析理论

2.1.1 预应力模态分析

多自由度结构系统的动力方程为

Ax″+Bx′+Lx=F(t)

(1)

式(1)中：A为系统质量矩阵；B为系统阻尼矩阵；L为系统刚度矩阵；x为结构位移列阵；x′为速度列阵；x″为加速度列阵；F(t)为载荷列阵。

系统经过简化后，无阻尼振动方程为

Ax″+Lx=0

(2)

常微分方程解为

x=Xsin(ωt+α)

(3)

式(3)中：X为振幅列阵；ω为固有频率；α为初相位。

将式(3)代入式(2)得

(L-ω2A)X=0

(4)

令Q=L-ω2A，detQ=0，即

(5)

式(5)中：l为刚度系数；a为质量系数。

通过求解行列式得出叶片固有频率为

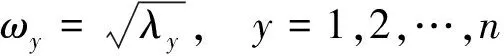
(6)

式(6)中：λ为线性方程组的特征值。

首先，在Workbench静力学模块中对叶片施加相应的转速进行仿真从而得到预应力，接着对叶片进行预应力下的模态分析。

2.1.2 谐响应分析

进一步了解涂层对叶片阻尼性能的影响，要对叶片进行频率响应分析。谐响应振动方程的一般形式为

Ax″+Bx′+Lx=Nsin(ωt)

(7)

式(7)中：N为激振载荷幅值。

对于线性时不变系统，式(7)通解的表达式为

X=X1(t)+X2(t)

(8)

式(8)中：X1(t)表示式(7)为齐次方程时的通解，在弱阻尼状态下的表达式为

X1(t)=He-βtsin(ωdt+ζ)

(9)

式(9)中：H为弱阻尼下的振幅；e为自然常数；β为载荷频率；ωd为弱阻尼下的载荷频率；ζ为相位。

X2(t)表示式(7)为非齐次方程时特解的一个简谐函数：

X2(t)=Jsin(ωt-φ)

(10)

式(10)中：J为强迫振动的振幅；φ为强迫振动相位。

故式(7)的通解表达式为

X(t)=He-βtsin(ωdt+ζ)+Jsin(ωt-φ)

(11)

2.2 分析结果

2.2.1 模态分析结果

对叶片进行带有预应力的模态分析，约束叶片根部两侧端面所有节点的自由度，施加固定约束。采用Block Lanczos模态提取法，分别提取无涂层叶片、涂敷不同厚度的单面涂层叶片和双面涂层叶片的前六阶模态。获取叶片的各阶固有频率对于避免叶片在旋转过程中发生共振具有重要意义，通过有限元分析所得固有频率如表2所示，硬涂层对叶片固有频率影响范围如图2所示，不同涂敷方式与无涂层叶片固有频率差值如图3所示。本文无涂层叶片、不同涂敷方式与厚度的叶片共7种，模拟结果显示7组模态振型是相同的，故只展示1组无涂层叶片振型如图4所示，其他6组均以无涂层叶片振型作参考。

对比了涂敷方式和厚度均不同的硬涂层和无涂层叶片的固有频率，从表2可以看出，涂层对叶片的一阶固有频率结果影响不大，但会明显降低第三阶、五阶、六阶的固有频率。从整个固有频率变化趋势来看，单面涂层和双面涂层叶片大致相同。单面涂敷0.20 mm对叶片第二阶固有频率影响最小，双面涂敷0.20 mm对叶片第三阶固有频率影响最大。由图2可知，硬涂层对叶片固有频率影响范围在0.1%～5.8%。

表2 无涂层和涂层叶片的固有频率

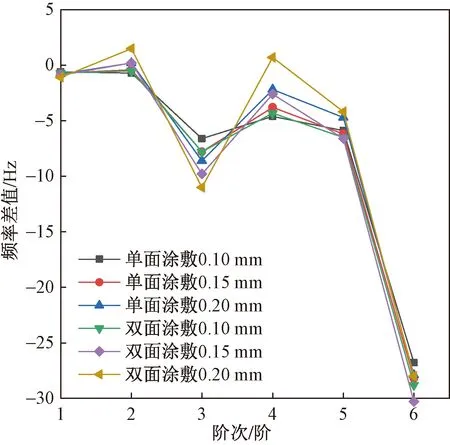
图3 硬涂层-高温合金叶片的固有频率差值对比Fig.3 Comparison of natural frequency difference between hard coated superalloy blades

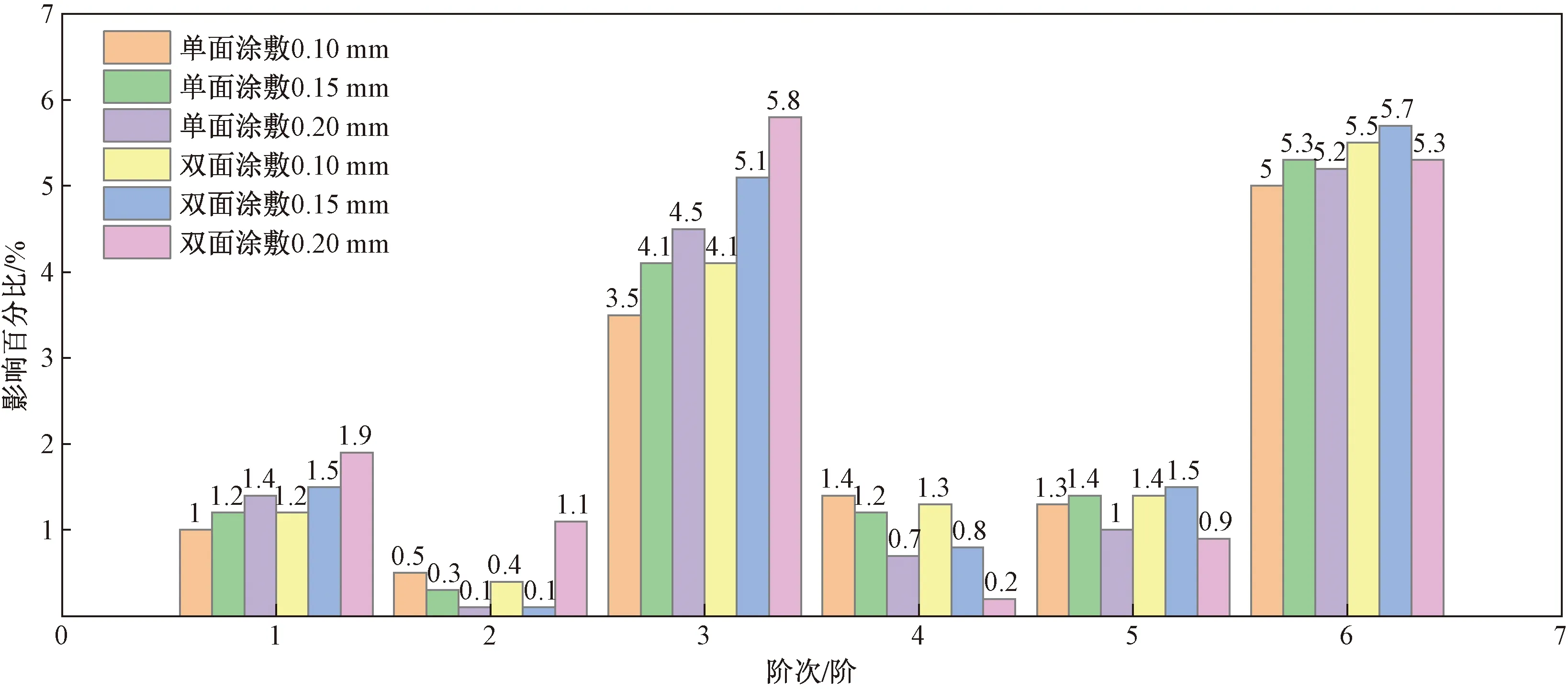
图2 硬涂层对高温合金叶片固有频率影响百分比Fig.2 Effect percentage of hard coating on natural frequency of superalloy blade

无涂层叶片振型如图4所示，而不同涂敷方式和厚度的叶片振型基本无变化，表明硬涂层对叶片振型无影响。叶片一阶振型出现横向条状线，为弯曲振动。三阶振型出现纵向条状线，为扭转振动。而二阶、四阶、五阶、六阶振型同时出现不规则的横纵条状线，则为弯扭振动。整个叶片的振动幅度以一阶的弯曲振动为主，最大变形出现在叶尖，最小变形出现在叶根附近，说明叶尖更容易发生变形及损坏。

图4 叶片振型Fig.4 Modes of blades

图5 等效应力云图Fig.5 Equivalent stress nephogram

在预应力模态分析下，无涂层叶片和单、双面分别涂敷0.20 mm叶片上表面的等效应力云图如图5所示。结果表明，在模拟实际工作环境中的叶片时，叶片所受最大等效应力分布在叶身中心区域。此外，无涂层叶片最大等效应力为501.41 MPa，而单面涂敷硬涂层叶片涂敷面的最大等效应力为221.28 MPa，双面涂敷硬涂层叶片涂敷面的最大等效应力为220.23 MPa。结果表明，双面涂敷0.20 mm的硬涂层对叶片的单面等效应力减小效果最为明显。

2.2.2 谐响应分析结果

分别对无涂层和单双面不同涂层厚度的叶片进行谐响应分析，分析方法采用模态叠加法。旨在得到叶片一阶固有频率附近的响应，故考虑叶片一阶固有频率范围，将谐响应的频率范围设置为0～100 Hz，激振力设为1g(g为重力加速度)的强迫振动。提取叶片叶尖为响应点，位移方向为Y方向。涂敷厚度不同的单面、双面涂层叶片与无涂层叶片位移响应对比如图6所示。

结果表明，在激振频率为58 Hz附近时，叶尖位移的振幅响应达到峰值，均出现在一阶固有频率附近。无涂层叶片、单、双面涂敷0.20 mm叶片响应峰值分别为0.441 07、0.285 31、 0.278 94。在单面涂层叶片响应对比中，涂敷0.10、0.15、0.20 mm叶片的响应峰值分别比无涂层叶片下降了28.3%、32.4%、35.3%；在双面涂层叶片响应对比中，涂敷0.10、0.15、0.20 mm叶片的响应峰值分别比无涂层叶片下降了35.4%、36.5%、36.8%。整体来看，双面涂敷0.20 mm的硬涂层叶片响应峰值最低，由此可见其减振效果显著，且双面涂敷比单面涂敷降低响应峰值2.2%。

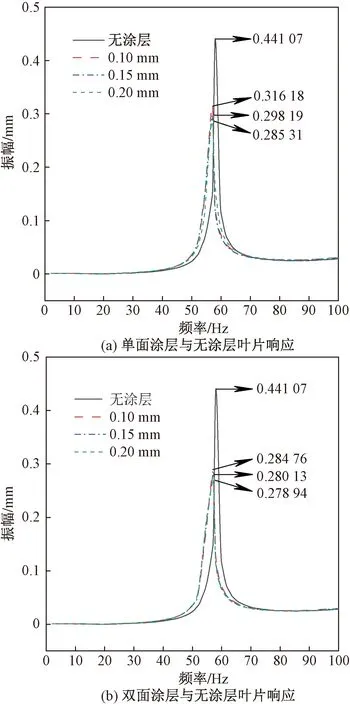
图6 单面、双面涂层叶片与无涂层叶片位移响应对比Fig.6 Comparison of displacement response between single and double coated blades and uncoated blades

通过对比分析的结果来看，在激励条件为1g加速度的情况下，涂敷方式不同、厚度不同的硬涂层叶片振动响应均有下降，其中下降最明显的是双面涂敷0.20 mm的叶片，说明其减振效果最显著。

3 共振分析

叶片在工作过程中难免会发生共振，将叶片工作转速范围设置在222～237 rad/s[11]。为了得到转速与共振的关系，选择减振效果最好的双面涂敷0.20 mm硬涂层叶片与无涂层叶片进行对比，绘制两者在不同转速下的坎贝尔图，如图7所示。激振频率射线是图中经过原点的射线，其中，k为激振力谐波系数。不同斜率代表叶片工作转速的n倍，横向曲线表示叶片转速与固有频率的关系。激振频率射线与每一阶横向曲线的交点为叶片在此阶固有频率下的共振点，对应的转速为共振转速。

当叶片振动频率和激振力频率满足式(12)时发生共振或谐共振：

Fi=kFe

(12)

图7 无涂层叶片和双面涂敷0.2 mm硬涂层叶片在不同转速下的坎贝尔图Fig.7 Campbell diagram of uncoated blades and 0.2 mm hard coated blades on both sides at different speeds

式(12)中：Fi为叶片振动频率；Fe为激振力频率；当k=1时称为共振，当k≠1时成为谐共振。

共振裕度是一种容限，其公式为

(13)

式(13)中：ni为共振转速；n为工作转速。当发动机叶片安全稳定工作时需要远大于共振裕度的10%。

图7(a)表明，在叶片工作转速范围内有两个共振点，分别出现在一、三倍频曲线与叶片第三、六阶固有频率的交点，对应的共振转速分别为231.7、235.1 rad/s，共振裕度分别0.7%、2.2%。在二倍频曲线与叶片第五阶固有频率的交点处，共振转速接近叶片工作转速的范围，为263.2 rad/s，共振裕度为14.4%。而在其他交点共振裕度均远大于10%。图7(b)表明，在一、二倍频曲线与双面涂敷0.2 mm涂层叶片第三、五阶固有频率出现交点，共振转速分别为232.5、234.2 rad/s，共振裕度分别为1.1%、1.8%。但叶片工作转速附近没有出现第三个交点，在其他交点，共振裕度均远大于10%。所以，叶片的工作转速应尽量避开共振点，从而在一定程度上避免共振。

4 结论

采用有限元方法对硬涂层叶片的振动特性问题进行研究，分析了硬涂层涂敷方式、涂层厚度对叶片的固有特性、谐响应以及共振的影响，结果表明硬涂层对叶片有明显的减振效果，得出如下结论。

(1)叶片的振动形式以弯曲振动为主，叶片单、双面涂敷NiCoCrAlY+YSZ涂层后对叶片固有频率影响范围分别为0.1%～5.3%、0.1%～5.8%，不同涂敷方式和厚度的硬涂层对叶片振型均没有影响。

(2)在模拟叶片实际的工作环境中，叶片所受最大等效应力位于叶片中心区域。且双面涂敷0.20 mm的硬涂层对叶片的单面等效应力减小效果最为明显。

(3)在相同的激励条件下，硬涂层叶片谐响应峰值均发生在一阶固有频率附近，随着NiCoCrAlY+YSZ涂层的涂敷方式和厚度的改变，叶尖响应峰值也随之改变。其中响应降低最显著的是双面涂敷0.20 mm的叶片模型，为36.8%。说明涂敷方式和涂敷厚度对叶片的减振效果均有影响。

(4)根据坎贝尔图可知，发动机叶片在每个共振交点下会发生不同程度的共振。在叶片工作转速范围内及附近，双面涂敷0.20 mm的硬涂层将叶片共振点由3 个减为2 个，减少了共振发生的可能性。