高等数学创设 初等数学解决

无锡市太湖格致中学 何 勇

在一些高考数学试题或模拟题的设置中，以创新情境等方式来巧妙设置，利用高等数学的知识来创设或应用，是新课标高考数学命题的一常见命题方式与创新亮点，倍受各方关注．此类创新应用问题，合理渗透初等数学与高等数学之间的联系，实现中等教育与高等教育之间的合理有机过渡与无缝衔接．

1 创新定义类问题

利用高等数学中一些概念、名称、相关知识等的初等数学化创新定义，通过初等数学知识来重新简单定义高等数学问题，结合合理推理论证或数学运算，实现用初等数学知识解决创新问题的目的．

A．4 B．3 C．2 D．1

分析：根据题目条件中给出的“凸函数”的创新定义，通过对给定的函数f(x)进行二次求导，结合二阶导函数在给定区间上的不等式恒成立进行等价转化，变换主元，将二次不等式恒成立问题转化为一次不等式恒成立问题，结合一次函数的图象与性质来确定变量的取值范围，进而确定区间“宽度”的最大值．

根据“凸函数”的定义，当|m|≤1时，f″(x)=x2-mx-6<0恒成立，等价于当|m|≤1时，关于m的一次函数h(m)=x2-mx-6<0恒成立.

从而b-a的最大值为2-(-2)=4.

故选择答案：A．

点评：借助高等数学中的“凸函数”进行创新定义，结合初等数学中一些基本初等函数的求导与运算，综合函数与方程、函数与不等式的转化与应用，利用函数的图象与性质实现问题的突破与解决．以创新定义的形式来实现高等数学知识与高中基本初等函数之间的链接．

2 公式应用类问题

利用高等数学中一些定理、性质、公式等的初等数学化表示，结合初等数学知识来展开与构建，合理利用推理论证或数学运算，实现借助高等数学知识简单快捷解决一些初等数学问题的目的．

A．a>b>cB．b>c>a

C．b>a>cD．c>b>a

分析：根据题目条件，合理联系条件中分式、指数式、根式等对应的泰勒公式，利用泰勒公式的展开式所对应的关系式的结构特征，快捷解决对应代数式的大小比较问题．

解析：根据泰勒公式，得

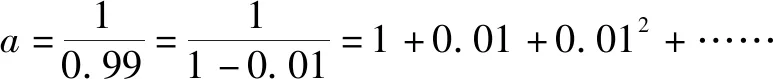
由上各展开式的关系，可知a>b>c.

故选择答案：A．

点评：借助高等数学中的泰勒公式，利用泰勒公式的展开，并结合三个代数式在泰勒公式条件下的进一步转化以及相应的结构特征，可以简单快捷地比较大小．泰勒公式是高等数学中的内容，是高中数学知识的拓展与课外提升部分，是高中数学竞赛中的知识点．

3 步骤分解类问题

利用高等数学中一些解题步骤、技巧策略等的初等数学化分解，在初等数学背景下按部就班，通过初等数学知识来合理推理论证或数学运算，实现用初等数学知识解决高等数学问题的目的．

例3(福建省莆田市2022届高中毕业班第二次教学质量检测数学试卷·12)(多选题)意大利数学家卡尔达诺(Cardano. Girolamo，1501—1576)发明了三次方程的代数解法．17世纪人们把卡尔达诺的解法推广并整理为四个步骤：

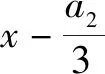
第二步，利用公式x3+y3+z3-3xyz=(x+y+z)(x+ωy+ω2z)(x+ω2y+ωz)将x3+px+q因式分解；

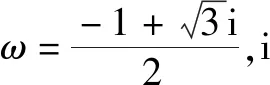
某同学利用上述方法解方程8x3-12x2-42x+55=0时，得到y的一个值：-1+i，则下列说法正确的是( ).

分析：根据题目条件，结合卡尔达诺的三次方程代数解法的四个步骤的说明与理解，按部就班，逐一展开与分析，综合复数的四则运算加以计算与处理，进而确定对应说法的正确性．

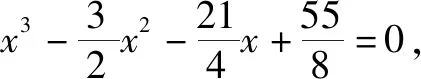
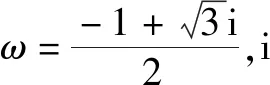
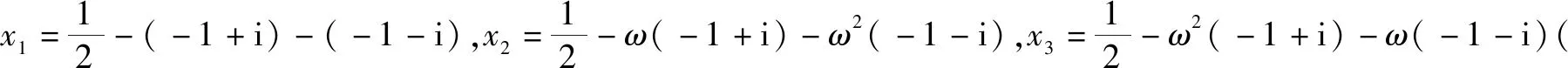
综上分析，故选择答案：ABC．

点评：借助高等数学中卡尔达诺的三次方程代数解法的步骤分解，结合数学运算、代数式的变形、因式分解以及复数的四则运算等的综合应用．此类问题涉及高等数学中的一些解题步骤的初等数学分解，关键就是按照说明按部就班，综合推理论证或数学运算加以解决．

通过高等数学中的某个数学概念的初等化定义或初等化应用、某个定理公式的展开与应用、某个解题步骤过程的初等化分解等创新设置，实现高等数学知识初等化，借助定义的理解、公式的应用、步骤的分析等加以拓展，从而实现相关知识在内涵与外延上的突破，考查学生的阅读理解能力、推理论证能力等，也对学生后续进入高校学习所具备的基本能力加以合理区分与选拔．