不畏浮云遮望眼 只缘“构造”在心头
——几种构造函数的方法在高考解题中的运用
周 萍
(江苏省昆山经济技术开发区高级中学 215300)
函数是高中数学的重要内容,近几年间构造函数法在高考试题中屡次出现.本文介绍几种构造函数的方法来解决高考数学试题.
1 用同构法构造函数
1.1 简单的函数构造
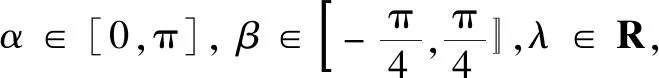
点评通过观察,这两个方程相似,所以只需结合三角公式将第二个方程进行适当的变形,便可得出与第一个方程相同的形式,再构造函数.
例2(2021年南通一模)若alna>blnb>clnc=1,则下列关系正确的是( ).
A.eb+clna>ec+alnb>ea+blnc
B.ec+alnb>eb+clna>ea+blnc
C.ea+blnc>ec+alnb>eb+clna
D.ea+blnc>eb+clna>ec+alnb

1.2 对称法构造函数
例3(2019年郑州三模)已知f(x)在R上存在导函数f′(x),对任意x∈R,有f(x)-f(-x)=x3,在(0,+∞)上有2f′(x)-3x2>0,若f(m-2)-f(m)≥-3m2+6m-4,则实数m的取值范围是( ).
A.[-1,1] B.(-∞,1]
C.[1,+∞) D.(-∞,-1]∪[1,+∞)
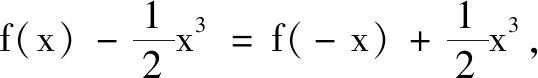
1.3 ex与ln x型同构式构造函数
此类同构式常用形式有xex和xlnx,即xex=eln xex,xlnx=(lnx)eln x;还有x+ex和x+ lnx,即x+ex=eln x+ex,x+lnx=eln x+lnx.
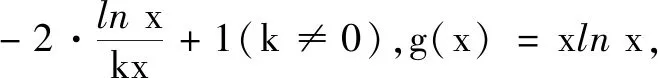
A.[1,+∞) B.[e,+∞)

例5(2020年新高考全国Ⅰ卷)已知函数f(x)=aex-1-lnx+lna.
(1)略;(2)若f(x)≥1,求a的取值范围.

点评同构式函数其实是复合函数的另一种改写方式,只要复合函数能解决的问题,同构式基本可随之解决.近几年高考中的一些不等式恒成立求参数范围问题、零点存在问题及不等式证明中,用同构式的方法屡次出现.
以上构造函数的方法主要可通过因式分解、移项、通分、除以同因式、两边取对数等手段,将方程或不等式“改头换面”,使其变成结构相同的方程或不等式,亦或是复合函数形式等,进而构造出较易解决的新函数.这就要求学生善于观察题设中的函数形式,挖掘其本质,并熟悉常见的函数形式,抽丝剥茧,系统分析.
2 用放缩法构造函数
在高中压轴题中,不等式的证明或者参数范围的求解往往蕴含较复杂的形式,需要利用不等式的传递性,将原有形式进行放大或缩小,进而简化求解过程.高中阶段最常用的有三种放缩,其原理都是利用曲线的切线,将指数、对数、三角函数放缩成一次函数形式.
2.1 基于指数放缩ex≥x+1构造函数
例6(2021年苏州期初调研)已知函数f(x)=xeax-lnx,其中a>0.
(1)略;(2)对于给定的常数a,若f(x)≥bx+1对x∈(0,+∞)恒成立,求证:b≤a.

点评本题函数结构较复杂,所以先“同构”,使得变量统一成ax+lnx这一整体,再立足于指数放缩式ex≥x+1,得到eax+ln x≥ax+ lnx+1,最终达到消除变量的目的.
2.2 基于对数放缩x-1≥ln x构造函数
例7(2021年南京一模)设函数f(x)=ax+e-x(a>1).
(1)求证:f(x)有极值点;
(2)设f(x)的极值点为x0,若对任意正整数a都有x0∈(m,n),其中m,n∈Z,求n-m的最小值.
点评本题中涵盖除变量x外的某些参数,受其结构和参数的影响,其处理步骤无法顺利进行,所以采用对数放缩x-1≥lnx,简化求解过程.
2.3 基于三角放缩sin x≤x≤tan x构造函数
例8(2021年八省联考)已知函数g(x)= ex+sinx+cosx.
(1)略;(2)若g(x)≥2+ax,求a.
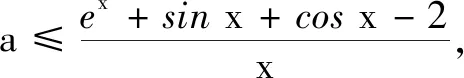
当x<0时,同理可得a≥2,故a=2.
点评本题将三角放缩和指数放缩完美结合,化曲为直,使放缩这一构造函数的方法在导数不等式的求解中大放异彩.
3 极值点偏移条件下的函数构造
在“极值点偏移”条件下构造函数,一般用于f(x)是连续函数,在(x1,x2)上有唯一极值点x0,且在f(x1)=f(x2)成立的前提下,x1,x2与极值点x0之间不等关系的证明.处理这类问题主要有以下两种方法.
3.1 主元对称化构造函数
例9(2021年新高考卷)已知f(x)=x(1- lnx).
——以指数、对数函数同构问题为例

