沁润数学文化 构建魅力课堂——对“阅读材料”的设计与思考

林梦蝶

(浙江省乐清市柳市镇第一中学 325604)

数学教材中的“阅读材料”是学生感受数学文化、体验数学魅力的真正所在，但却往往被教师所忽略，致使学生失去用数学方式看待、理解真实生活的一条途径，数学核心素养也未能得以完全发展．《义务教育数学课程标准(2022年版)》中提出核心素养的构成要求：会用数学的眼光观察世界、会用数学的思维思考现实世界、会用数学的语言表达现实世界．本文基于数学文化的教学模式[1]，以浙教版九年级上册阅读材料“精彩的分形”为例，从感受数学美、积极探索数学美、主动追求数学美三个层次，使学生获得跨学科学习的体验，逐步培养学生的几何直观、推理能力、创新意识等核心素养．

1 内容分析

本节内容安排在九年级上册第4章“相似三角形”后，教材内容主要分成三部分．首先，利用等边三角形一步步构造出科赫雪花，并给出分形、迭代等概念；其次，给出一组图片，欣赏蕨类植物中的分形；最后，利用等腰直角三角形构造出“分形龙”，并提出实践活动要求．

教材设计好的教学思路：由经验触动(你是否观察过雪花的形状)，到数学化理解(感受其图形变换特点和数量特点)，再到多领域渗透(美术、计算机等)．基于教材和九年级学生的思维特点，确立了以下六条教学目标：(1)从图形的周长、面积等理解图形的数量特点；(2)能推导出n次迭代后科赫雪花的周长、面积等的代数式；(3)理解科赫雪花“具有有限的面积，但有着无限周长”这一特点；(4)掌握分形、迭代、自相似的概念；(5)感受分形的应用价值； (6)能动手设计一个简单的分形图形．

2 教学过程

2.1 经验触动

播放北京冬奥会开幕式相关视频．

师：这是独具中国人浪漫与自信的开幕式．这部分场景的核心元素是什么？

生：雪花！

师：这是张艺谋导演心中的雪花．昨天你们画了自己心目中的雪花(展示学生画作)．你见过雪花吗？有仔细观察过吗？

师：这是显微镜下的真实雪花(图1)，这是数学家科赫画出来的雪花(图2)．科赫选择了一个简单的基础图形，经过四次重复操作就画出几乎与真实雪花重合的图形．

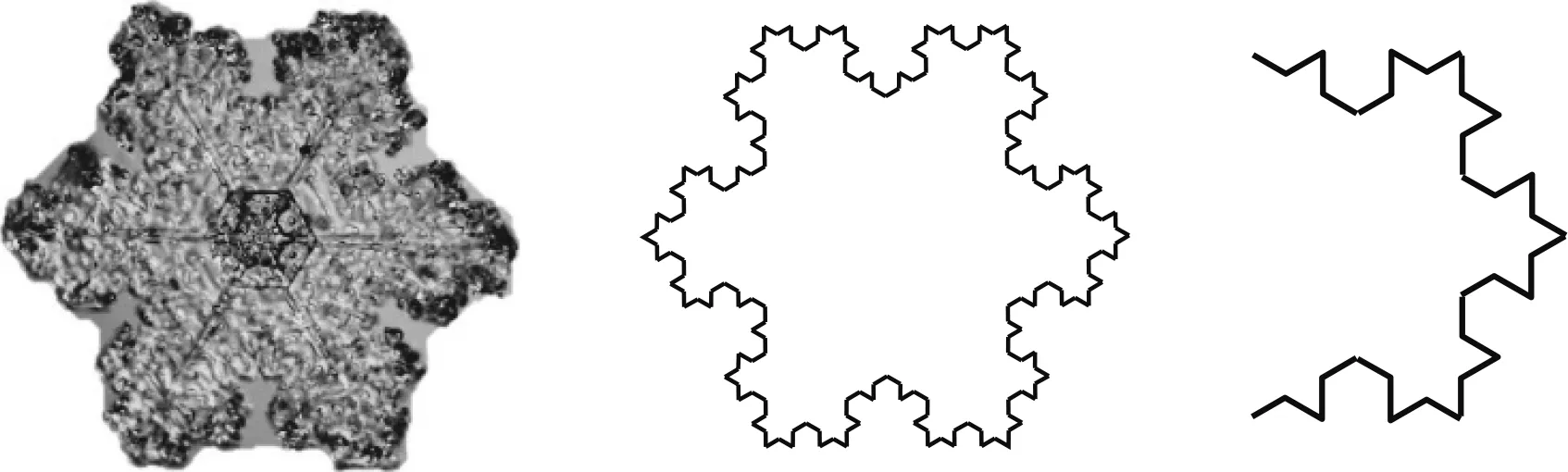
图1 图2 图3

问题1你能看出科赫选择了一个什么基础图形？

生：局部放大(图3)，等边三角形．

设计意图由北京冬奥会开幕式中的雪花到学生笔下的雪花，再到数学家科赫画的雪花，从学生已有的经验出发，引起认知冲突(如何画一朵真正的雪花)，从而激发学生学习分形的兴趣．另外，引导学生用基本几何图形解释、建构真实世界，逐步培养学生用数学方式去思考世界的习惯．

2.2 数学化理解

如图4，科赫先画出一个等边三角形，然后构造出了图5的形状．

图4 图5 图6

问题2科赫是怎么操作的？

生：可以看作等边三角形的三边新生长出三个小等边三角形．

师生活动：(共同总结)对等边三角形的每一条边进行：①三等分；②以居中那条线段为底边向外作等边三角形；③擦掉所作等边三角形的底边．

问题3对图5再进行一次刚刚的操作，能想象出它会变成什么样吗？将其画在网格中．

学生活动：在由等边三角形构成的网格中，学生画出图6．

设计意图通过观察，引导学生用数学语言描述出迭代的步骤，加深对迭代的理解；让学生在网格中画出第1次、第2次的迭代图形，理解科赫雪花的自相似过程，并加深对几何直观、应用意识等核心素养的培养．

师(板书)：像这样重复反馈的活动，称为“迭代”．每一次对过程的重复称为一次“迭代”，而每一次迭代得到的结果会作为下一次迭代的初始值．

问题4将图5局部放大，它的结构看起来和图4有什么关联？将图6局部放大，它的结构看起来和图5有什么关联？

生：相似．

师(板书)：将细微部分放大后，其结构看起来仍与原先的一样，这种图形叫做分形，这种现象叫做自相似．这种自相似的过程可以无限地进行下去．

问题5如果将图6继续迭代一次，图形会变成什么样？

生：每一条边长出更小的等边三角形．

追问1 如果无限地迭代下去，这个雪花有什么特点？

追问2 从数学角度了解、研究图形特点可以从哪些视角入手？

生：角度(角度是图形非常重要的研究对象，但自相似不会导致角度变化)．

生：边长，周长，面积．

师：完成表格．

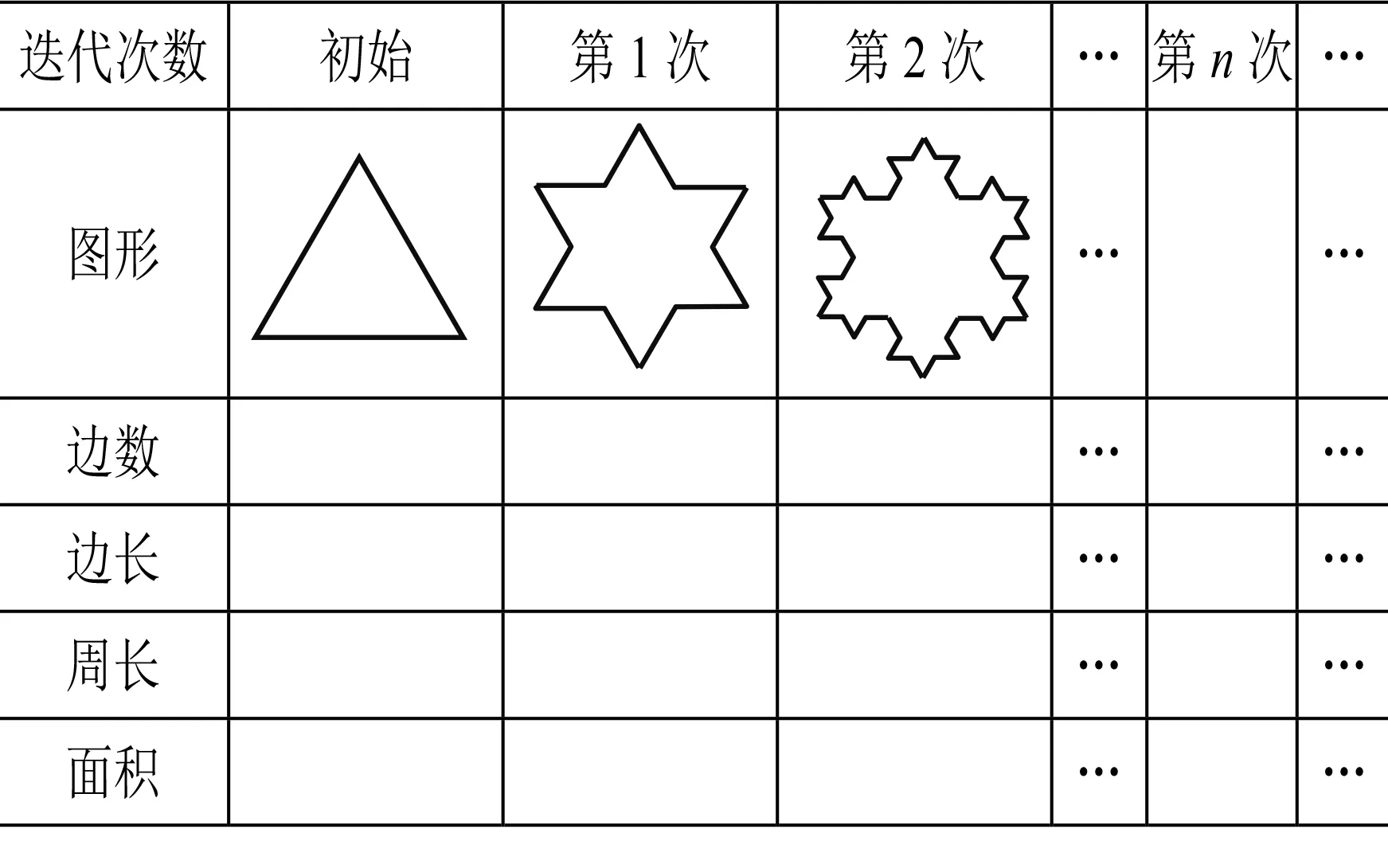
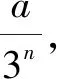
设计意图由初始图象到第1次、第2次迭代，再到第n次迭代，探索图形变换过程中边数、边长、周长、面积的数量变化规律，加深对迭代这一变化的数学内部规律的理解，培养学生主动运用数学解释现实生活的意识．

问题6n取一个越来越大的数，乃至变成无穷大时，边数、边长、周长、面积有何特点？

生：边数、周长越来越大，变成无穷大；边长越来越小，变成无穷小；面积虽然在增加，但是增加得越来越慢．

师：慢到后面是什么情况？代数不直观，我们借助几何．(展示动图)可以发现，在不断的迭代过程中，科赫雪花一直包含在初始等边三角形的外切圆中．因此，雪花的面积不会无穷大，而是一个有限的值．

师生活动(共同归纳)：科赫雪花具有有限的面积，但有无限的周长．

设计意图边数、边长、周长能用简洁的代数式表示，故n次迭代后的特点能较好地总结出来；但n次迭代后的面积难以化简，需要借助几何直观加以理解．

2.3 多领域渗透

师：像这样同时具有“有限”和“无限”的概念，对许多科学家有着巨大的吸引力．物理学家惠勒就曾这么说：“将来谁不知道分形概念，也不能称为有知识．”可以看出，分形在他心中有着多么崇高的地位．

设计意图进行哲学领域的渗透．数学和哲学本身具有非常密切的关联，许多著名的数学家，如笛卡尔、莱布尼兹等，本身也是哲学家．走向数学文化哲学，将最大限度地整合数学史、数学社会学、数学思维、数学艺术、数学美学等研究方向，从而使数学哲学具有更广阔的发展空间[2]．学生因此也能更直观地感受到数学文化哲学的魅力．

师生活动(共同欣赏)：第一类是分形三大怪物(科赫雪花、谢尔宾斯基三角、谢尔宾斯基海绵)；第二类是常见的简单分形；第三类是生活中的分形(树叶、罗马花椰菜、闪电、海岸线)；第四类是细胞分化．

师：谢尔宾斯基三角，能够更好地印证分形图形“面积有限而周长无限”的特点．

设计意图欣赏分形三大怪物，增加关于纯粹数学的基本知识；欣赏常见的简单分形，帮助学生后期能画出一些简单分形，增强数学基本技能；欣赏生活中的数学，让学生学会用数学的眼光观察世界；欣赏细胞分化中的分形，让学生用数学的思维思考世界．

问题7上述分形的初始图形分别是什么？如何自相似进行迭代的？

问题8分形能应用在哪里？

师生活动(共同总结)：分形包括两类应用．第一类为显性应用，包括服装、地图、陶瓷纹路等设计，以及电影特效制作等．第二类为隐性应用，包括预测生态系统的演化、分析金融市场趋势等．

设计意图使学生感受图形几何的巨大应用价值，以及数学在社会发展中的实践价值．作为图形显性的价值当然是用于各种设计，但是图形背后的数学规律和特点则可推动更多交叉领域的发展．数学当之无愧为基础学科．

问题9完成两个设计任务．(1)绘制一个简单分形；(2)以分形为核心，利用扭扭棒进行设计．

学生活动1：进行创作设计．展示的同时，说明设计原理(图7～图10)．

图7 图8 图9 图10

设计意图基于对科赫雪花迭代的学习，学生能够设计的作品一般局限于基本图形(三角形、正方形、圆等)的边长进行三等分或者四等分，再向外或向内进行自相似．这样很有局限性，后续展示分形龙的迭代方式，有助于充实对分形概念的理解．

学生活动2：利用扭扭棒进行分形设计与展示(图11～图14)．

图11 图12 图13 图14

设计意图进行艺术设计领域的渗透．新版课标初中阶段的综合与实践领域明确要求采取项目式的学习方式，以问题解决为导向，整合数学与其他学科的知识和思想方法，发展创新意识和实践能力．在项目化学习方式中理解分形的显性特征——使艺术具有数学美，数学具有艺术美，学生感受艺术创作或者数学实验的快乐．

师：用计算机编程展示“分形龙”第十次的迭代效果．

问题10你们已经掌握了科赫构造分形雪花的基本步骤．还有其他构造自相似的方法．如图17的“分形龙”的初始图形为等腰直角三角形(图15)，你能观察出它是如何得到图16的吗？

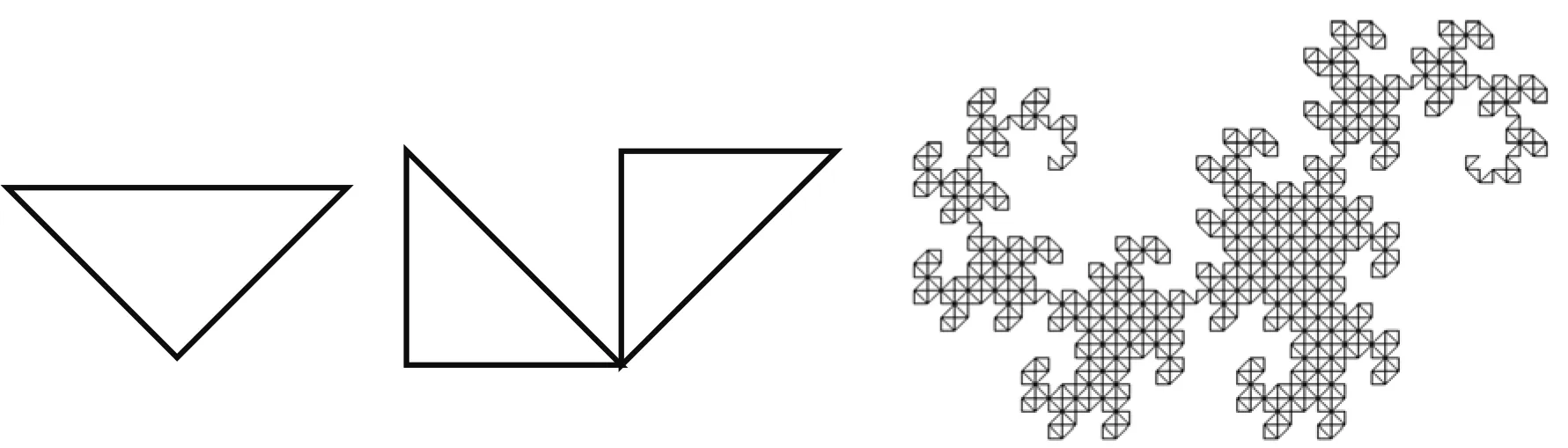
图15 图16 图17

生：将等边三角形分割成两个全等的三角形，右边一半不动，左边一半以斜边所在的直线为轴作轴对称．

设计意图进行计算机领域的渗透．分形作为计算机图形学的产物，在某种程度上证明了科学与艺术结合的可能性[3]．计算机的融入，帮助学生探索分形更多奇妙和有趣的结论．

2.4 回顾反思

问题11总结一下，根据科赫设计雪花的步骤，我们如何进行分形设计？

师生活动(共同总结)：设计分形的步骤：①选择初始图形；②设计自相似：相似(缩放)→图形变换(旋转、平移、轴对称)；③开始迭代．

师：最后，希望你们如同科赫雪花一般，在这有限的时间内，创造无限的美好与可能．

设计意图在教学中渗透德育．有限和无限是一对辩证统一的概念，在分形中，学生感受到这对概念，延伸到实际生活中，带来数学与哲学整合碰撞的精彩火花．以辩证观去理解、欣赏数学深层次的辩证统一美[4]．

3 进一步思考

浙教版的六册数学教材中共出现19篇阅读材料．常规教学中，不少教师往往忽略这部分“边角料”，坦言根本就没有上过这些内容，因而关于阅读材料的教学设计更是少之越少．但这部分“边角料”反而才是唤醒学生数学兴趣、激发学生数学热情和学生自主创造数学应用价值的核心素材．只有充分利用好这部分内容，学生的数学核心素养才能真正得以落地．

(1)趣味性

趣味性是使学生投入到学习的第一抓手．很多数学公式和定理具有严谨的抽象性，学生望之却步．因此在进行教学设计时，要抓住教学内容的特点，触动学生已有经验，注意多领域渗透带来的非凡数学体验．同时，阅读材料的内容本身已经非常有吸引力，如“地球有多大”“谁将获得最后一个小组出线名额”“美妙的镶嵌”等等(均为浙教版)．教师可以尝试用一节课甚至十几分钟，让学生关注这部分内容，及时开展教学．

(2)拓展性

拓展性不仅意味着对现有数学知识的完善和补充，也意味着对数学体系的扩充，亦即高阶数学观念的渗透．从小学的自然数到初中的实数，学生完成的是对数系的扩充．类似地，本节“精彩的分形”则是让学生感受到图形几何学的扩充．传统几何学之所以被描述为无生气的(cold)和枯燥乏味的(dry)的，一个很重要的原因是它不能描绘云彩、山脉、海岸线、树木等物体的自然形状．传统的欧氏几何中，线、面、体都是光滑、有统一规律的，但这样有统一规律的事物在实际生活中只是一小部分．分形几何却能描绘更多曲折、破碎事物的不统一规律．

(3)实验性

数学实验意味着赋予数学更多的活动操作，学生获得更多的实践活动经验．如“有趣的拼图”“美妙的镶嵌”“立体图的一种画法”等等，都是进行数学实验设计的内容．数学学习不仅仅只是为了应付考试和升学，当下社会赋予数学学习更多的内涵．正如新课标中提出的三大修订原则——坚持目标导向、坚持问题导向、坚持创新导向，都推动教师要更加关注学生的数学应用意识和创新意识等核心素养．这部分核心素养单凭做题和考试很难培养，因而可以通过数学实验赋予数学教学更多的活力和可能性．