基于人脸特征的可搜索加密方案
徐慧华 杨 雄
1(福建师范大学协和学院经济与法学系 福建 福州 350117)2(福州大学至诚学院计算机工程系 福建 福州 350002)
0 引 言
一个典型的人脸识别系统首先采集人脸图像,对其进行一些预处理后提取高维特征。在用户注册过程中,这些特征向量和用户的身份标签一起存储于数据库中。在用户身份认证过程中使用该数据库来验证一个人所声称的身份,身份验证过程即通过计算所声称身份的用户人脸特征与该身份标签在数据库中所对应的人脸特征之间的相似度来完成。针对人脸识别系统最直接的攻击点就是网络传输的人脸特征和人脸特征数据库。因此,若将人脸特征直接以明文形式进行网络传输和存储于数据库中,会严重影响注册用户的隐私和认证系统的安全性。
为了提高人脸识别系统的安全性,可利用密码系统对网络传输和数据库中存储的人脸特征进行加密。然而,一般的加密方案还需要将人脸特征密文进行解密才能够完成人脸匹配所需的基本算术运算。而同态加密方案支持对密文进行人脸匹配所需的算术运算[1],能够在加密域中实现人脸匹配,不需要对人脸特征密文解密,进一步提升了安全性。同态加密系统分为部分同态加密(Partially Homomorphic Encryption,PHE)[2]、somewhat同态加密[3]和全同态加密(Fully Homomorphic Encryption,FHE)[4]。虽然全同态加密在加密域支持无限的加法和乘法运算,比部分同态加密和somewhat同态加密在实际场景中更为通用,但随之带来的计算复杂度也更高。
目前流行的人脸匹配方法大多为基于深度神经网络的方案,这些方案通过卷积神经网络模型[5-7]从人脸图像中提取出高维人脸特征后,计算人脸特征向量之间的欧氏距离,取最小距离所对应的人脸图像的身份作为测试人脸图像的身份。但在加密域中进行人脸匹配时,数百到上千维的人脸特征向量需要非常耗时的同态操作,导致其不适合在高维向量空间中进行运算[8]。
本文基于全同态加密方案CKKS[9]提出了一种高效的解决方案,探索了使用全同态加密的人脸特征进行人脸匹配的实用性。首先将典型的人脸匹配度量(欧氏距离)分解为一系列加法和乘法运算的组合;接着,利用中国剩余定理和批处理技术,通过旋转加密向量,以logn个同态加法的代价实现n个同态加法,降低计算复杂度;最后,再利用近似最近邻算法,以O(logN)的代价实现1 ∶N的人脸匹配,满足实际应用场景的需求。
1 方案设计
一个典型人脸识别系统的人脸特征数据库包含了由已注册用户人脸特征组成的集合。当进行身份认证时,需要将测试人脸特征向量与集合中的各个人脸特征向量进行欧氏距离的计算,计算结果即为特征向量间的相异程度。假设待测试人脸的特征向量为x,集合中待匹配的人脸特征向量为y,将x和y之间的相异度定义为d(x,y),那么d(x,y)为:
(1)
式中:n为所提取的人脸特征维度。
从式(1)可知,人脸的匹配过程包含了n个向量元素的减法(x1-y1)、n个向量元素的乘法(平方)和n个向量元素的累加求和。
在全同态加密方案中定义加密函数f对人脸特征z进行加密:ε(z)=f(z;θp),其中θp为公钥;同时z=g(ε(z);θs),其中g(.;θs)为带私钥θs的解密函数。在保护原始人脸特征z的同时,也必须保证在加密域中进行计算而不会损失精度,即:
d(ε(x),ε(y))=d(f(x;θp),f(y;θp))
g(d(ε(x),ε(y));θs)≈d(x,y)
(2)
1.1 用户注册和身份认证协议
本节描述基于全同态加密方案的用户注册和身份认证协议。考虑具有两个实体的场景:一个用户和一个数据库。
在系统初始化阶段,需要执行以下步骤:生成一对公私密钥对,公钥为θp,私钥为θs;将私钥保存在认证服务器中,对外发布公钥。
1.1.1注册协议
在注册阶段,标识为c的用户需要执行如下步骤:
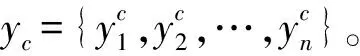
(2) 使用公钥θp加密用户的人脸特征值yc,将人脸特征的同态密文ε(yc)与该用户身份标签一起保存到数据库中。
注册过程如图1所示。
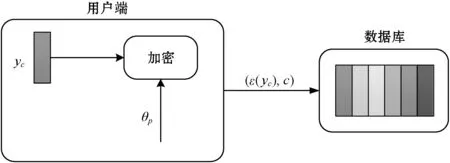
图1 用户注册过程
1.1.2身份认证协议
在此阶段,将通过以下步骤对用户进行身份认证:
(1) 采集待认证用户的人脸图像并提取其特征值x,并使用公钥θp加密。
(2) 计算待认证用户的加密人脸特征ε(x)与数据库中的所有加密人脸特征ε(y)之间的相异度d(ε(x),ε(y))。
(3) 使用私钥θs分别对各个密文的计算结果进行解密,将满足阈值要求的最小相异度对应的用户身份标签返回。
身份认证过程如图2所示。
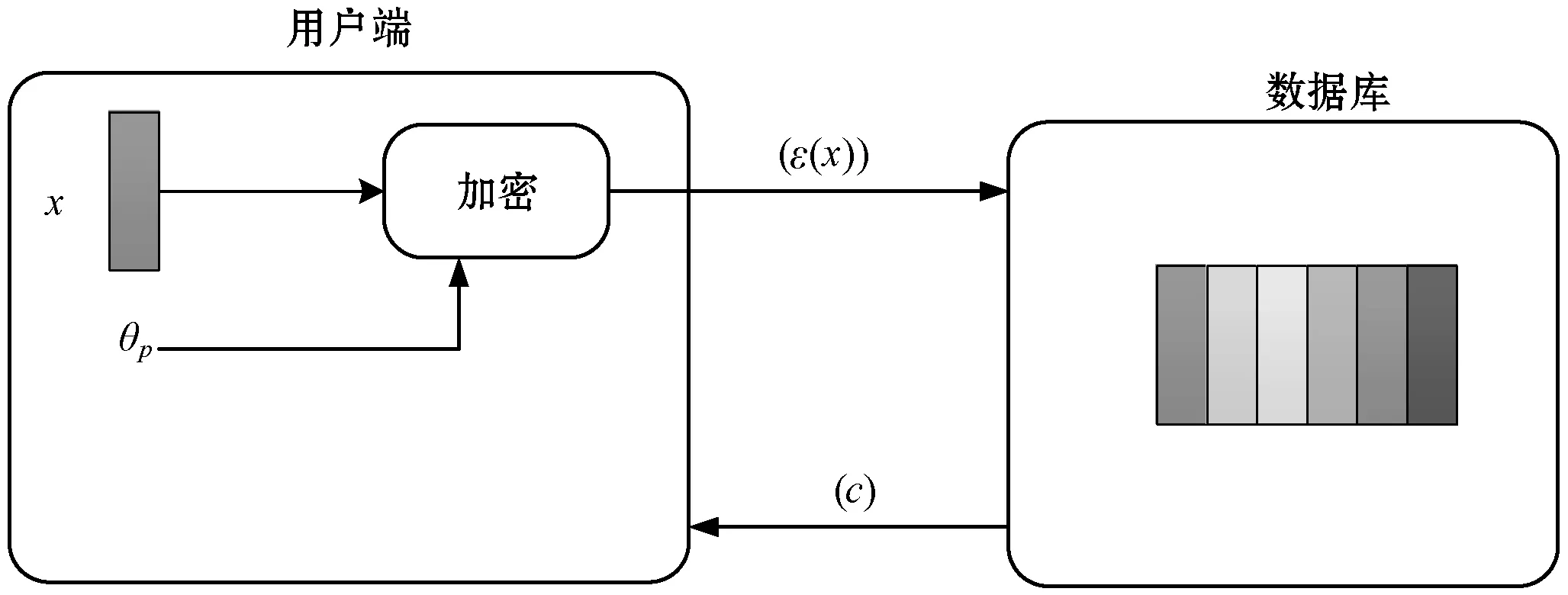
图2 用户身份认证过程
1.2 基于CKKS方案的高效人脸匹配
1.2.1全同态加密方案
由于人脸特征值是以浮点数表示,因此全同态加密选用支持浮点数的CKKS方案。
本系统的全同态加密方案包含以下5个步骤:
(1)GenKey(λ):生成一对公私钥。根据输入的安全参数λ生成公钥θp和私钥θs。
(2)Encrypt(m,θp):使用公钥θp加密消息m,计算生成密文c。
(3)Add(c0,c1):输入两个密文c0和c1,计算求得这两个密文的和c0+c1。
(4)Multiply(c0,c1):输入两个密文c0和c1,计算求得这两个密文的乘积c0×c1。
(5)Decrypt(c′,θs):根据密文c′,利用私钥θs计算出明文m′。
1.2.2加密域中的人脸相异度的计算
式(1)中描述的人脸相似度可在加密域中描述为:
d(x,y)≈d(cx,cy)
(3)
式中:cx和cy分别为特征向量x和y的密文。d(cx,cy)的欧氏距离的计算为:
式中:n为人脸特征维度
该计算可分别为3个步骤:
(1) 对密文cx和cy进行减法运算:cz=Add(cx,-cy)。
(2) 对密文减法运算的结果进行乘法运算:cz=Multiply(cz,cz)。
(3) 最后还需要对cz中各个元素进行累加运算,得到欧氏距离的平方。由于全同态加密不支持平方根操作,因此在加密域中仅求得欧氏距离平方的密文。
那么在加密域中计算欧氏距离则需要n次的加密乘法运算和n-1次的加密加法运算。但由于每次对加密数据的乘法运算量很大,导致在加密域中计算人脸相似度的速度非常缓慢,尤其在人脸特征高维度表示的场景下该问题会进一步加剧。
1.2.3批处理
在加密域进行人脸匹配的主要瓶颈在于计算人脸相异度时所需的全同态加乘法次数与特征维度n呈线性关系。Brakerski等[10]提出了一种可针对数字向量进行同态加密和解密的技术,而不是每次仅使操作单个数字。该技术利用中国剩余定理(Chinese Remainder Theorem,CRT)将n个数编码到同一个多项式上。那么对于两个n维的人脸特征向量x和y,通过将包含n个向量元素的特征向量通过批处理整体加密至单个密文中,将n个向量元素密文的加法和乘法操作转换为单个向量密文的加法和乘法操作,即在单次同态计算操作的时间内完成n次同态加法或乘法运算。因此,随着一次批处理数量的增加,可显著提高计算效率。通过批处理技术可完美完成加密域中人脸相异度计算的步骤(1)和步骤(2)。
但由于批处理方案是将向量整体加密,导致无法访问加密后向量中的各个元素,也就无法完成步骤(3)中的各个元素累加运算,存在一定的局限性。但可以通过Gentry等[11]提出的循环旋转logn次向量并累加,获得加密向量中的各元素之和。
以4维向量为例,通过循环旋转计算各元素和的过程如图3所示。
对于512维的人脸特征向量,原先步骤(3)中511次同态密文的加法运算现在只需9次的循环和加法运算,进一步减轻了计算负担。
综上,基于CKKS方案的人脸匹配计算的实现关键代码如下:
(1) 生成密钥:
parms=EncryptionParameters(scheme_type.CKKS)
poly_modulus_degree=8192
parms.set_poly_modulus_degree(poly_modulus_degree)
parms.set_coeff_modulus(CoeffModulus.Create(
poly_modulus_degree,[60,40,40,60//))
context=SEALContext.Create(parms)
scale=pow(2.0,40)
keygen=KeyGenerator(context)
evaluator=Evaluator(context)
public_key=keygen.public_key()
secret_key=keygen.secret_key()
relin_keys=keygen.relin_keys()
gal_keys=keygen.galois_keys()
在本方案中使用的多项式模度poly_modulus_degree为8 192,配合近似最近邻搜索方法中每个集合最多剩余4个点。
(2) 使用公钥对人脸特征向量进行加密:
encryptor=Encryptor(context,public_key)
face_vector=np.loadtxt(data,delimiter=′,′)
inputs=DoubleVector(face_vector)
plain=Plaintext()
encoder.encode(inputs,scale,plain)
encrypted=Ciphertext()
encryptor.encrypt(plain,encrypted)
(3) 在加密域中计算人脸相异度:
#向量密文的减法操作,结果存入x_encrypted
evaluator.sub_inplace(x_encrypted,y_encrypted)
#向量密文的乘法操作,结果存入x_encrypted
evaluator.square_inplace(x_encrypted);
evaluator.relinearize_inplace(x_encrypted,relin_keys)
rotate_encrypted=Ciphertext()
result_encrypted=x_encrypted
#通过循环旋转和累加计算元素密文和
i=1
while i<512:
evaluator.rotate_vector(result_encrypted,i,gal_keys,rotate_encrypted)
evaluator.add_inplace(result_encrypted,rotate_encrypted)
i*=2
(4) 使用私钥获取特征向量欧氏距离的平方和:
decryptor=Decryptor(context,secret_key)
plain_result=Plaintext()
decryptor.decrypt(result_encrypted,plain_result)
result=DoubleVector()
encoder.decode(plain_result,result)
return(result[0]**0.5)
1.3 基于Annoy搜索算法的人脸识别
人脸识别身份认证的过程就是将待认证用户的人脸特征与数据库中的所有人脸特征一一进行相异度的比较,将满足阈值要求的最小相异度所对应的用户身份标签返回。倘若对每一个人脸都进行比较,那计算的时间复杂度为O(n)。由于相同的人脸得到的人脸特征索引都是比较类似,因此可以采用高效的Annoy(Approximate Nearest Neighbors Oh Yeah)算法对人脸特征创建索引。
Annoy算法的目标是建立一棵(群)二叉树的数据结构,基于该数据结构能够在较短的时间内找到任何查询点的最近点,其查询的平均时间复杂度为O(logn)。
(1) 建立索引。以2维数据集为例,Annoy算法首先随机选择两个数据点,并以这两个点为初始中心节点,执行聚类数为2的KMeans聚类,产生收敛后的两个聚类中心点。在中心点的连线上(灰色短线)建立一条垂直线(黑色粗线)把数据空间分成两部分。在多维空间中该黑色粗线即为等距垂直超平面。如图4所示。

图4 建立索引过程
然后在划分的两个子空间中继续进行递归迭代,直到每个子空间中最多只剩下K个数据节点。在该方案中K值为4。
最终,通过多次递归迭代划分,原始数据点会形成一个二叉树结构。二叉树的叶子节点记录原始数据节点,中间节点则记录的是分割超平面的信息。
(2) 查询过程。完成索引建立之后,对一个数据点进行查找相似节点集合过程就是二叉树的根节点不停向叶子节点遍历的过程。通过对二叉树每个中间节点(分割超平面相关信息)和查询数据节点进行距离度量来确定二叉树遍历过程是继续往这个中间节点的左子树还是右子树遍历。
建立索引和查询依赖于节点之间的距离度量。本方案在开源库中欧氏距离方式的基础上增加了全同态密文的欧氏距离度量方式,其实现代码与在加密域中计算人脸相异度类似。二叉树中间节点(等距垂直超平面)通过两个聚类中心点各维度上的均值得到,在加密域中通过一次加法和乘法操作(乘以0.5)即可完成。
(3) 1 ∶K批量计算。上述查找过程完成后,返回的叶子节点中包含了至多K个人脸特征密文,最后还需要计算待认证用户的人脸特征与该叶子节点中各个人脸特征的欧氏距离。
在全同态加密方式中使用的多项式模度poly_modulus_degree为8 192,其支持整体加密的向量长度最大为4 096。因此可通过旋转操作将叶子节点中的所有人脸特征密文(以至多4个为例)构造于同一个密文中,合并后的密文结构如图5所示。

图5 合并后的密文结构
在合并后的密文结构中各个密文向量之间分别填充一个全0的512维向量,待认证用户的人脸特征同样构造上述密文结构,最后就可以利用批处理技术就可以同时计算单个待认证用户人脸特征密文与K个人脸特征密文的欧氏距离。
2 系统测试
在系统仿真测试中基于人脸数据集(LFW)和基于深度神经网络的人脸模型FaceNet(512维)进行测试。
本系统的服务端使用Python语言在Centos 7上开发,测试处理器为腾讯云单核2 GB配置的云服务器,CPU型号为Intel(R) Xeon(R) CPU E5- 26xx v4。同态加密算法采用微软开源的简单加密算法函数库SEAL(Simple Encrypted Arithmetic Library)的Python版本PySEAL。
2.1 准确率测试
人脸数据集(LFW)中共包含了13 233幅人脸图像,获取数据集中的所有人脸特征信息后,将未加密情况下两个人脸特征向量之间的欧氏距离与它们在加密域中计算出来的欧氏距离进行比较,部分数据如表1所示。
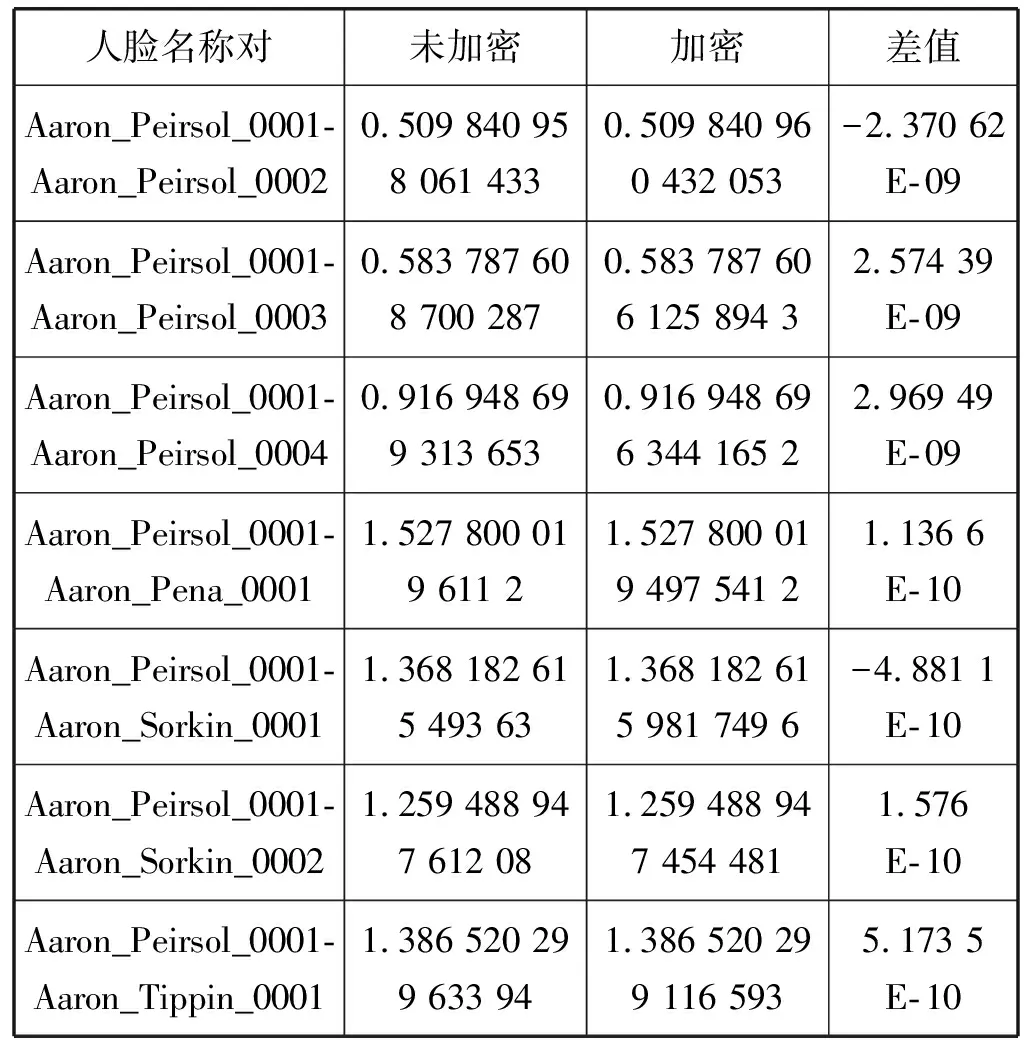
表1 未加密与加密人脸特征向量欧氏距离对比
从表1可知,加密后计算的人脸特征的欧氏距离能够达到未加密人脸特征的水准,因此能够保持原生算法的人脸识别准确率。
2.2 全同态性能
测试全同态计算过程中加密、欧氏距离计算(1 ∶4)和解密的用时情况,并与未加密情况进行对比,部分数据的操作用时如表2和表3所示。
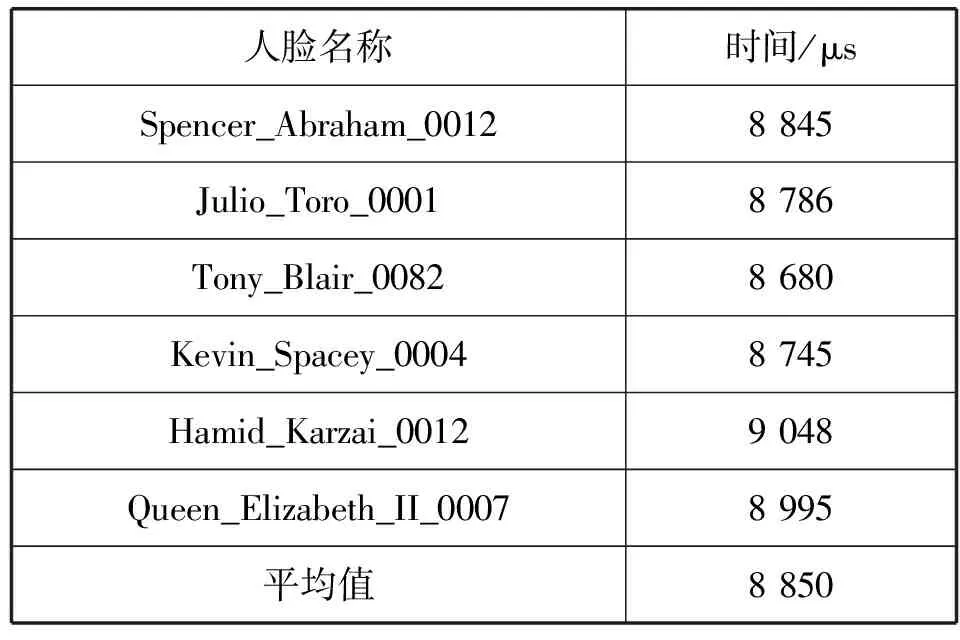
表2 加密过程用时
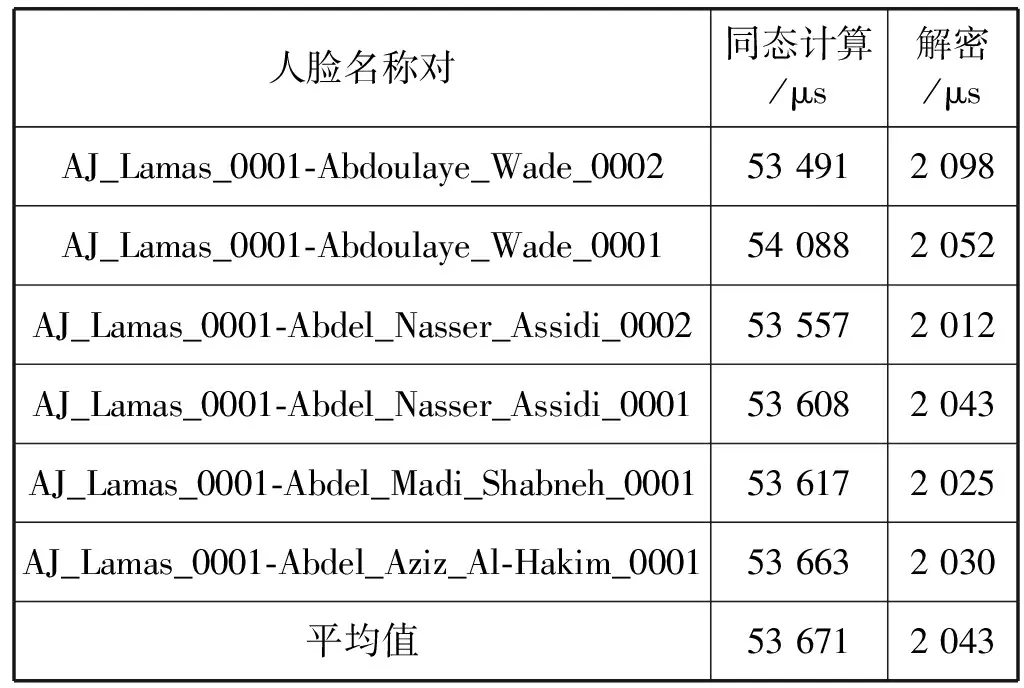
表3 加密域中同态计算和解密操作用时
从表2可知,在注册过程中的人脸特征加密的平均用时为8 850 μs。
从表3可知,在认证过程中一对密文向量欧氏距离的同态计算用时平均为53 671 μs,密文解密时间平均为2 043 μs。在本方案的安全参数配置下,1 ∶4密文向量的同态计算用时与一对密文向量计算用时是一致的,因此在Annoy所建立的二叉树中叶子节点中密文特征向量个数为4的情况下一对人脸特征密文欧氏距离的平均用时为13 418 μs。
未加密情况下一对人脸特征向量直接进行欧氏距离的平均用时为546 μs。综上,未加密与加密情况下人脸特征距离的用时情况如表4所示。
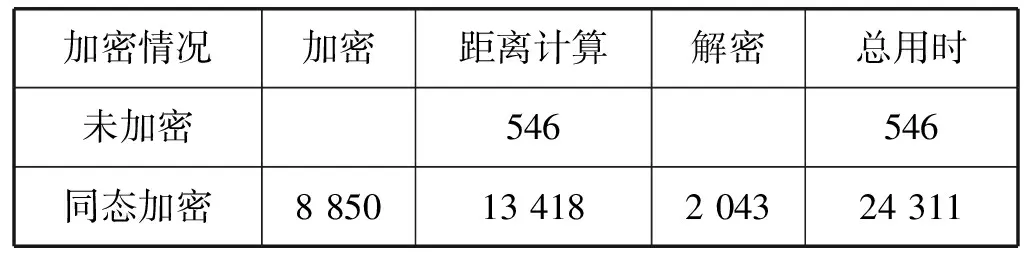
表4 未加密与加密情况下欧氏距离计算用时 单位:μs
从表4可知,在实验环境中,使用全同态加密后一对人脸特征之间的欧氏距离计算的总用时大约为0.02 s,是未加密的45倍左右。
系统的整体架构为C/S架构,其中客户端为用户提供了注册和登录服务,服务器端提供了全同态计算和人脸认识服务。不考虑摄像头采集人脸所花费的时间,以LFW数据集中的人脸模拟系统的注册和登录。加密前后人脸注册的全过程用时如表5所示。
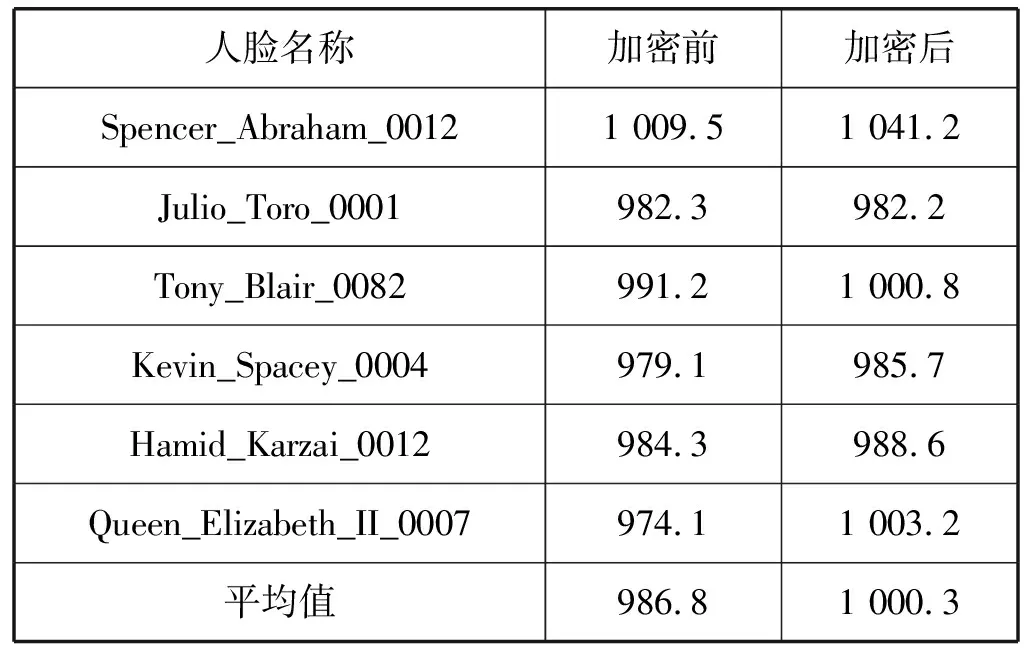
表5 注册全过程用时 单位:ms
人脸数据库中已存储1 000个人脸特征密文,认证全过程用时如表6所示。
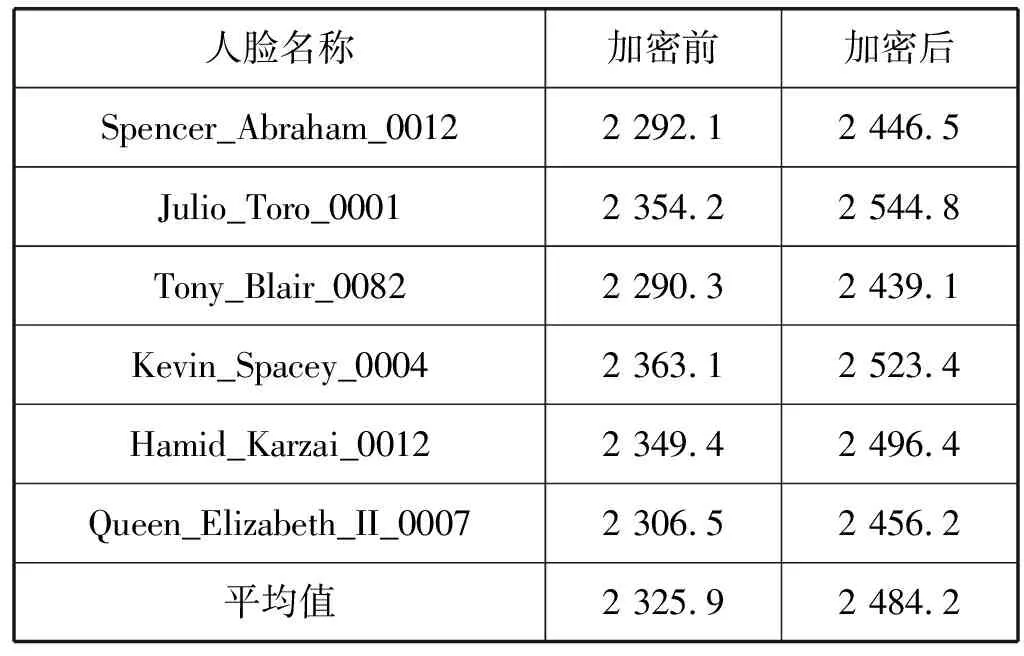
表6 认证全过程用时 单位:ms
测试结果表明:注册过程中,加密后的平均用时为1 000.3 ms,相比加密前大约增加了13.5 ms,提高了不到2%,占注册总用时的1.3%。而在认证过程中,加密后总用时平均为2 484.2 ms,相比加密前大约增加了158.3 ms,提高了6.8%,占认证总用时的6.37%。
从系统整体视角分析,图形界面载入用时和网络通信部分的用时最长,而同态加解密和计算用时占总用时大约5%。因此对人脸特征密文进行全同态计算的效率是能够满足实际应用需求的。
3 结 语
随着信息技术的快速发展,信息安全已成为人们重点关注的领域。本文探讨了使用全同态加密来保护人脸特征的实用性。首先,利用了一个批处理方案,实现了在单次同态计算操作的时间内完成n次同态加法或乘法运算,提高了在加密域中人脸匹配的效率;进一步利用近似最近邻搜索算法,显著提高了人脸识别的效率。在提供人脸模板保护、防止信息泄漏和保护用户隐私的同时,基于全同态人脸的匹配能够保持原生算法的人脸识别准确率,在性能上也可满足实际应用的需求。

