一种基于势能模型的数据流聚类算法

舒 越 解 庆 刘永坚 唐伶俐

(武汉理工大学计算机科学与技术学院 湖北 武汉 430070)

0 引 言

随着信息技术不断发展，信息的传播效率不断提高，各种信息充斥着整个世界，各种高效的智能化数据采集技术投入市场应用，使信息数据的处理能力不断增强，而如何更加精准地从大量信息中挖掘出有价值的信息，是近些年学者们关注的重点之一[1]。随着数据流的爆发增长，比如金融数据、Web日志数据和视频监控数据等，数据流挖掘引起了学者们的关注[2]。数据流[3]是一个连续不断的数字信号序列，具有以下三个特性[4]。(1) 无限性：因为数据流持续不断地产生，因而数据点的数量是无限的，不能直接将其全部存储到内存中。(2) 动态演变性：数据分布和特征随时间推移而不断变化。(3) 实时性：数据流实时产生，需要被实时处理。这些特点给数据流处理带来了不小的挑战[5-6]:由于数据流无法全部存储在内存中，对数据流只能扫描一次；由于数据流的动态演变性，随着时间的推移，数据可能发生变化，即“概念漂移”问题；需要具有处理离群点的能力。

很多旨在解决数据流聚类问题的算法已经被提出，其中大部分是基于传统聚类算法扩展而来，如：K-means算法、DBSCAN算法和Affinity Propagation Clustering算法等，将这些传统聚类算法改进适用于数据流聚类。除此之外，很多数据流聚类算法沿用在线/离线两阶段数据流聚类框架[7]，在线阶段旨在构建概要数据结构，离线阶段根据这些概要数据结构使用聚类算法得到最终聚类结果。由于大部分数据流聚类算法以距离作为相似度度量标准，这造成对噪点敏感的问题，聚类效果不理想。

针对这个问题，本文提出一种基于势能模型的层次聚类算法PHAStream，该算法结合在线/离线两阶段数据流聚类框架[7]和基于势能模型的层次聚类算法PHA[8]，在线阶段采用融合势能和距离的相似度度量标准更新微簇，判断新到达数据点是否合并进现有微簇或新建微簇，并每隔一定时间采取剪枝策略删除过期的微簇，调整所有微簇的类型；离线阶段计算所有正常微簇的势能，构建边缘加权树和树状图，得到最终聚类结果。

本文的主要贡献包括：(1) 使用一种新的概要数据结构，它不仅记录数据点属性的统计信息、权重信息和时间戳信息，还有微簇之间的距离信息。它可以快速构建距离矩阵，方便计算微簇的势能，为后续基于势能和距离的相似度度量标准和微簇聚类提供基础。(2) 以势能和距离为相似度度量标准，在线阶段判断新到达数据点可能合并的微簇，然后根据势能判断是否合并进该微簇或新建微簇。传统以距离为相似度度量标准的方法中，新到达数据点是否合并进微簇会受到噪点的干扰，以势能和距离为相似度度量标准，可以减少噪点的干扰。(3) 将基于势能的层次聚类算法PHA改进适用于数据流聚类，可以减少噪点对聚类的影响，提高聚类效果。

1 相关工作

目前学术界对数据流聚类算法的研究已经取得不少成果，主要分为基于划分的方法、基于层次的方法、基于密度的方法、基于网格的方法和基于模型的方法五种。

第一种是基于划分的数据流聚类方法，实践操作较为简单，但必须在操作之前对聚类簇的数量进行设置，数据流的分布形态在初期阶段很难明确，聚类簇的数量很难得到准确的评估和预测。比如，Youn等[9]提出使用滑动窗口的基于划分的数据流聚类算法，该算法为每个窗口移动生成集群，由于在所有更改的窗口上重复进行聚类，会造成内存和计算时间方面的低效，所以此算法仅考虑窗口的插入和删除元组。

第二种是基于层次的数据流聚类方法，在数据的划分方面以微簇为主。如CluStream算法[7]，该算法提出了在线/离线两阶段数据流聚类框架，在线阶段以增量的方式更新微簇，离线阶段根据用户要求，使用K-means算法对微簇进行聚类。该算法操作简单，但是基于距离的相似度度量使得其对噪点较为敏感。

第三种是基于密度的数据流聚类方法，能够实现对任意形状的数据流进行划分，但是在计算过程中需要设置大量初始参数。如DenStream算法[10]，该算法沿用在线/离线两阶段数据流聚类框架，在线阶段将新到达的数据点分配给距离它最近的微簇，进行微聚类，同时提出了核心微簇、潜在核心微簇和噪点微簇来区分正常微簇数据、可能成为正常簇的微簇数据和噪点数据；离线阶段使用DBSCAN算法来聚类。

第四种是基于网格的数据流聚类方法，对聚类数据的形状没有约束限制，但是网格粒度的大小对聚类的质量有较大影响。D-Stream算法[11]是基于网格的数据流聚类算法之一，该算法沿用在线/离线两阶段数据流聚类框架，在线阶段将每个输入的数据点映射到网格中，离线阶段对这些密度网格进行聚类，并且取出稀疏的网格。张冬月等[12]提出基于网格耦合的数据流聚类算法，该算法在聚类过程中，不再片面地单独处理网格，而是将每个网格之间的耦合关系纳入考虑的范围内，网格之间的耦合关系可以更加精准地表现数据点之间的相似度，从而提升聚类质量。

第五种是基于模型的数据流聚类方法，需要大量的学科领域知识作为辅助，在使用中需要假设模型的支持。例如，朱颖雯等[13]提出的基于欧拉核的数据流聚类算法，该算法首先采用欧拉核的方式，显式地将数据点映射到同一维度的复数特征空间，接着在这个特征空间中使用GNG(Growing Neural Gas)模型进行聚类。

2 势能模型

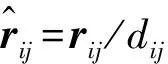
假设无穷远处的势能为0，那么数据点xi来自数据点xj的势能为：

(2)

在势能模型中，只需要关注势能的相对值，万有引力常数并没有影响，所以为了方便计算，将G设置为1，并假设每个数据点的质量为1，于是式(2)可改写为：

数据点xi的势能，表示为来自其他所有数据点对它产生的势能：

(4)

式中：N就是所有数据点的个数。

距离阈值ε的选取需要考虑数据点的分布，可以通过距离矩阵来进行计算：

ε=mean(MinDi)/S

(6)

式中：MinDi表示数据点xi和其他数据点之间的最短距离;S为比例因子。由文献[14]可知，取S=10时，模型可以达到较好的平衡状态。

在势能模型中，通常相似的数据点之间势能的差值也比较小，距离也更近，基于势能和距离的聚类方法以该规律为基础进行设计。

3 基于势能模型的数据流聚类算法

本节详细介绍基于势能模型的数据流聚类算法PHAStream，该算法结合在线/离线两阶段数据流聚类框架和基于势能模型的层次聚类算法PHA，算法的流程如图1所示。

图1 PHAStream算法流程

3.1 PHAStream算法初始化阶段

数据流是一段连续不断的序列点X={X0,X1,…,Xn,…}，每个数据点到达的时间分别为T={t0,t1, …,tn,…}，每个数据点在数据空间中是一个d维向量。

考虑不同到达时间的数据点的重要性，对每个数据点加权，利用一个衰减系数来确定权重与时间的关系。使用式(7)来作为衰减函数，其中λ>0，并且t表示当前时间戳tcurrent和该点到达的时间戳tarrival的差值，即t=tcurrent-tarrival。

w(t)=2-λt

(7)

在初始化阶段，模型初始化参数并把时间戳t设置为0，对初始长度的数据点使用PHA进行聚类，得到首批微簇。对于每个微簇，模型定义聚类特征向量来记录微簇的统计信息。借鉴StrDip算法[15]的聚类特征向量，本文提出一种改进的聚类特征向量，主要由带权重的微簇统计信息、微簇的权重和微簇之间的距离信息组成。距离信息可以快速构建距离矩阵，进而快速计算势能。聚类特征向量以这种形式定义: (CFx1,tl,weight,n,t0,dist_arr)。

(2)tl: 微簇中最后到达点的时间戳。

(4)n:微簇中所有数据点的个数。

(5)t0：微簇被创建的时间戳。

(6)dist_arr：当前微簇中心点和所有微簇中心点(包括自己)的距离组成的数组。

基于聚类特征向量，每个微簇的中心可以通过式(8)计算。

3.2 PHAStream算法在线阶段

在线阶段，对于每个新到达的数据点，寻找其可能合并的微簇，并判断是否合并进该微簇或者新建微簇，并更新聚类特征向量，每隔固定时间采用剪枝操作，删除过期的微簇并调整所有微簇的类型。

(1) 寻找目标微簇。当模型接收到一个新数据点的时候，需要在现有微簇中找到与之最相似的微簇，即其最可能合并进的目标微簇。

由文献[8，16]可知，在势能场中，距离矩阵和势能分别反映了数据点的局部和全局分布，同时可以发现同一个簇中的数据点，势能差值小且相互距离更近，所以这里提出一个新的相似判断标准pd值，如式(9)所示，来找到新数据点的“目标微簇”。

pd[i]=abs(Φc-Φi)×distci

(9)

式中：Φc表示新到达数据点的势能；Φi表示微簇i的势能；distci表示新到达数据点和微簇i的距离，pd[i]则表示新到达数据点跟微簇i的势能差绝对值和距离的乘积，因为同一个类中的数据点，势能差值小且相互距离越近，所以取pd[i]最小值时，微簇i是新到达数据点的“目标微簇”。

(2) 微簇的合并准则。当找到目标微簇之后，模型需要判断新到达点需要合并到目标微簇中，还是新建一个微簇。为此，需要设计一个合并准则来进行判断。

由文献[17]可知，一般情况下，由于数据集中噪点的数量是远小于正常数据点的数量，同时噪点的分布也相对稀疏，从数据点的概率分布特点和势能大小分析可知，噪点的势能相对正常数据点更大，从势能角度，这一特点正是区别正常数据点和噪点的关键。如图2所示[17]，是一个带有噪点的数据集，将每个数据点的势能按从小到大排序，如图3所示[17]，会出现一个“拐点”C，这个C点被称为“势能拐点”，“势能拐点”之后的数据点被认为是噪点。

图2 含有噪点的数据集

图3 势能递增图

将“势能拐点”作为一个新的合并准则，来判断新到达数据点是否合并进“目标微簇”。根据上述内容，由于此时已经可以求出每个微簇的势能，将新到达的数据点构成的微簇和其他所有微簇的势能按从小到大的顺序排列，构成势能递增图，根据式(10)找到当前势能场下的“势能拐点”。如果新到达数据点微簇的势能和“目标微簇”的势能均在“势能拐点”之前，那么在当前势能场下，新到达数据点微簇和 “目标微簇”均属于正常数据点，所以将新到达数据点合并进“目标微簇”中。否则，以新到达的数据点新建一个微簇。

(Φi-Φi+1)×(Φi+1-Φi+2)≤0

(10)

(3) 更新微簇与新建微簇。根据微簇的合并准则，当新到达数据点和其目标微簇的势能都在“势能拐点”之前时，那么就将新到达的数据点合并进目标微簇中；否则，以新到达数据点单独成为一个微簇，构建CF向量。

假设直到tc才有数据点x被吸收进微簇i，并且i接收上一个点的时间戳为tl，那么带有权重的微簇统计信息将以下列方式更新[15]:

weight=weight×2-λ(tc-tl)+1

(11)

CFx1=CFx1×2-λ(tc-tl)+x

(12)

通过式(11)和式(12)，可以快速地更新一个微簇新的权重weight和CFx1。

CF向量中的dist_arr属性，记录着当前微簇和其他微簇之间的距离信息，虽然不是以增量的方式更新，但是更新的代价并不大，因为在新的数据点到达时，要么将新到达数据点合并进某个微簇，要么以新到达的数据点新增一个微簇，如果处于检查周期，那么就删除过期微簇，期间这三种操作涉及个别微簇，或者只需要更新每个微簇dist_arr属性中个别距离值。dist_arr属性可以大大提高离线阶段进行聚类的效率。

(4) 删除微簇与调整微簇类型。微簇随着时间推移，会根据衰退函数改变权重，微簇的权重大于等于预设的权重阈值μ，则为正常微簇，反之，则为噪点微簇。

随着时间的推移，数据流的分布可能发生变化，一些“正常微簇”可能很长时间没有接收新的数据点，变为“噪点微簇”，这个现象我们称为“概念漂移”。所以需要每隔固定时间来检查所有微簇的权重，假设一个“正常微簇”的原始权重恰好是μ，经过Tg个时间戳，这个“正常微簇”刚好变为“噪点微簇”，此时Tg就是“正常微簇”变为“噪点微簇”的最小时间间隔[10，15]，即2-λTgμ+1=μ，求得：

为了节省PHAStream算法的运行时间，每隔Tg个时间戳就采用一种剪枝策略：将权重足够小的微簇删除。通过式(14)来判断一个微簇的权重是否足够小[10,15]，微簇的权重下限定义如下：

到达检查时间时，通过式(14)判断是否存在需要删除的微簇，如果存在需要删除的微簇，那么需要更新那些未删除微簇的dist_arr属性，将每个dist_arr属性中与删除微簇相关的距离信息全部删除。

3.3 PHAStream算法离线阶段

当有聚类要求时，使用改进的PHA(算法1)对所有“正常微簇”进行聚类，将每个微簇当作一个数据点，假设每个数据点的质量为1，那么每个微簇的质量等于微簇中数据点的个数。将每个微簇的dist_arr属性组合在一起，即此刻所有微簇的距离矩阵，根据势能模型，即可求出每个微簇的势能。为了实现所有数据点的聚类，采用一种边缘加权树技术[8]，基于所有数据的势能和距离对数据点进行高效组织。将所有数据点中势能最小的数据点当作“根节点”，记为xroot。

算法1改进的PHA

输入：距离矩阵dist_matrix_arr, 质量数组mass, 最终聚类簇个数K。

输出：聚类标签clusterLabels。

1. 计算每个微簇的势能，得到势能数组Potential；

2. 构建边缘加权树，并得到父节点数组parent和权重数组weight；

3. 构建树状图，依次合并最相似的微簇，直至微簇个数等于最终聚类簇个数K，得到聚类标签clusterLabels；

4. 返回聚类标签clusterLabels

对于每个数据点i，在所有其他数据点中势能值小于或等于i的所有其他数据点中距i最近的数据点称为i的父节点[7]，并表示为parent[i]。

由式(15)可以找到各自数据点的父节点，其中将根节点xroot的父节点定义为它自己，边缘加权树中边的权重，由数据点和其父节点之间的距离决定[7]，即：

weight[i]=disti,parent[i]

(16)

其中，根节点的权重是“无限大”。

可以通过以下步骤来构建边缘加权树：(1) 根据势能模型，求出所有数据点的势能，并将所有数据点按势能从小到大的顺序排列；(2) 将所有数据点中具有势能最低值的数据点设置为根节点xroot；(3) 根据数据点的势能递增顺序，依次找到剩余数据点xi的父节点parent[i]，并且将剩余数据点与其父节点之间的距离记录为weight[i]，然后加入到边缘加权树中；(4) 输出最后构成的边缘加权树。

3.4 PHAStream算法及复杂度分析

算法2是PHAStream算法的整体步骤，第1-4行是初始化阶段，计算检查时间Tg，使用PHA对初始长度的数据点进行聚类，得到首批微簇并创建CF向量。第5-17行是PHAStream算法的在线阶段，对于每个新到达的数据点x，如果数据点x和其目标微簇均在势能拐点之前，那么就将这个点合并进其目标微簇中，并更新其CF向量。否则，创建一个新的微簇和CF向量。每Tg个时间戳就检查调整所有微簇的类型，并采用剪枝策略删除过期的微簇。第18-20行是PHAStream算法的离线阶段，当有聚类要求时，根据所有正常微簇的dist_arr属性构建距离矩阵，计算势能，构建边缘加权树和树状图，得到最终聚类结果。

算法2PHAStream算入：数据流dataStream, 初始长度initNumber, 初始聚类个数q, 最终聚类簇个数K, 权重μ, 衰变因数λ。

输出：最终聚类结果。

1. 初始化时间戳timestampt= 0；

2. 计算周期检查时间Tg；

3. 使用PHA对初始长度的数据点进行聚类，得到首批微簇；

4. 为每个微簇构建CF向量，也称为微簇；

5. while (流数据未结束) do

6.t++；

7. for (每个新到达的数据点x) do

8. 寻找数据点x的目标微簇i；

9. if (数据点x和目标微簇i的势能均在势能拐点之前) then

10. 将数据点x合并进目标微簇i；

11. else

12. 新建一个微簇，并构建CF向量；

13. end if

14. end for

15. if (到达检查时间) then

16. 采用剪枝策略，并调整微簇类型；

17. end if

18. if (当有聚类要求时) then

19. 使用改进的PHA对所有正常微簇进行聚类；

20. end if

21. end while

PHAStream算法的在线阶段，计算成本主要在寻找“目标微簇”和合并准则判断。当新到达数据点寻找“目标微簇”时，需要遍历一遍现有的微簇，计算现有微簇和新到达数据点的距离，并将此距离更新进每个微簇的dist_arr属性，时间复杂度为O(n)。合并准则判断时，根据每个微簇的dist_arr属性可以构成距离矩阵，进而计算每个微簇的势能，将每个微簇的势能按从小到大排序，使用快速排序即可，时间复杂度为O(nlogn)。当到达检查时间时，遍历每个微簇检查其权重，是否存在需要删除的微簇，如果有，删除这些微簇，并将剩余未删除微簇中的dist_arr属性进行更新，删除dist_arr属性中与删除微簇相关的距离信息，时间复杂度为O(n)。

PHAStream算法的离线阶段，当有聚类要求时，根据每个微簇的dist_arr属性可以构成距离矩阵，将距离矩阵直接传入PHA，节约初始阶段计算距离矩阵的计算成本，接着构建“边缘加权树”和“树状图”，根据最终聚类簇个数K得到最终聚类结果，根据PHAStream算法的初始阶段所述，此处的时间复杂度为O(n2)。

4 实验与结果分析

4.1 实验环境

不失一般性，在所有实验中都规定每个时间戳只有1个数据点到达，并且到达的数据点经过在线阶段处理后，在指定时间戳陆续执行聚类。将本文算法效果与CluStream算法[6]、DenStream算法[10]、StrAP算法[18]和TEDA算法[19]进行对比，算法实验平台为：操作系统Ubuntu 18.04，Intel(R) Xeon(R) CPU E5-2673 v3 @ 2.40 GHz，内存64 GB，Python版本3.7。

4.2 数据集描述

数据集采用KDD-CUP99数据集和一组真实空气质量数据集进行测试。

KDD-CUP99数据集，一共有4 898 431个数据点，每个数据有41个维度，本实验选取34个连续属性，使用前1%样本数据集进行测试，数据集总共有50 000条记录，每隔5 000个数据点进行一次聚类测试。

真实空气质量数据集，选取北京市过去2016年1月1日到2019年12月31日，每天24个小时的空气质量数据，共有35 064条数据，其中无效数据有5 026条，故最终使用的有效数据为30 038条，每条数据具有7个属性，只取PM2.5、PM10、CO、SO2、NO2、O3作为测试属性，使用AQI作为分类标签，如表1所示。每隔5 000个数据点进行一次聚类测试。

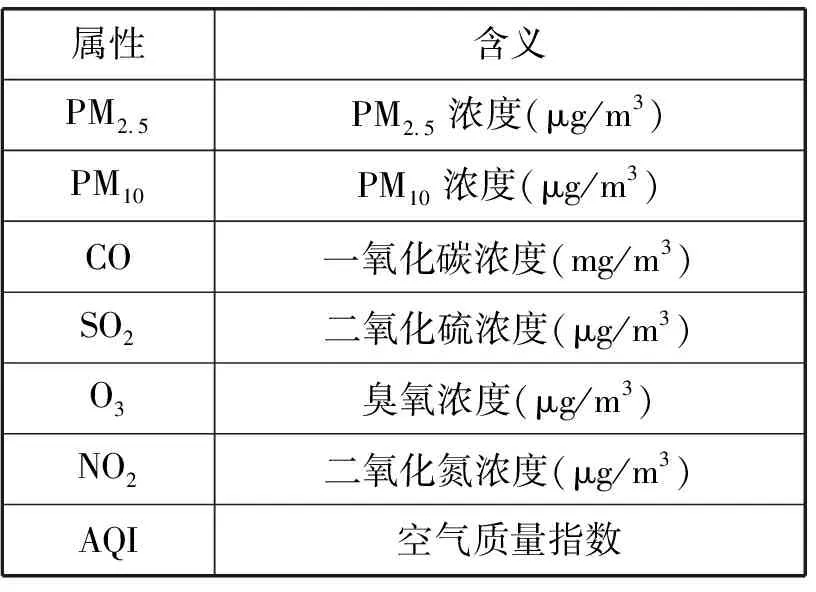
表1 空气质量数据集属性

4.3 度量标准

本实验以聚类质量SSQ和聚类纯度Purity作为度量标准。聚类质量SSQ的定义如下：

SSQ=∑d(pi,ci)2

(17)

式中：pi是每个数据点;ci是pi最近的聚类微簇中心。即通过计算所有点到各自聚类中心距离的平方和来衡量聚类质量SSQ，SSQ越小，说明效果越好。

聚类纯度Purity的定义如下：

(18)

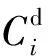
4.4 模型参数设置

本实验本文中所有试验的初始长度initNumber均为500， 通过控制变量法，来对区分正常微簇和噪点微簇的权重μ、衰变因数λ、初始聚类个数q和最终聚类簇个数K进行参数设置实验。由4.3节聚类度量标准可知，SSQ越小越好，Purity越大越好，定义变量p来表示由SSQ和Purity总体反映的聚类效果：

故变量p的值越小，聚类效果越好，通过控制变量法，来进行参数设置实验。

图4至图7分别是KDD-CUP99数据集对权重μ、衰变因数λ、初始聚类个数q和最终聚类簇个数K参数的聚类效果对比图。根据式(19)可知，p值越小越好，所以μ值、λ值、q值和K值分别在区间[1.7, 2.0]、 [0.1,0.15]、[325,450]、[5,15]之间取值为佳。综合实验得出，当μ=2.0，λ=0.13，q=400，K=15时聚类效果最好。

图4 KDD-CUP99数据集不同μ值聚类效果对比图

图5 KDD-CUP99数据集不同λ值聚类效果对比图

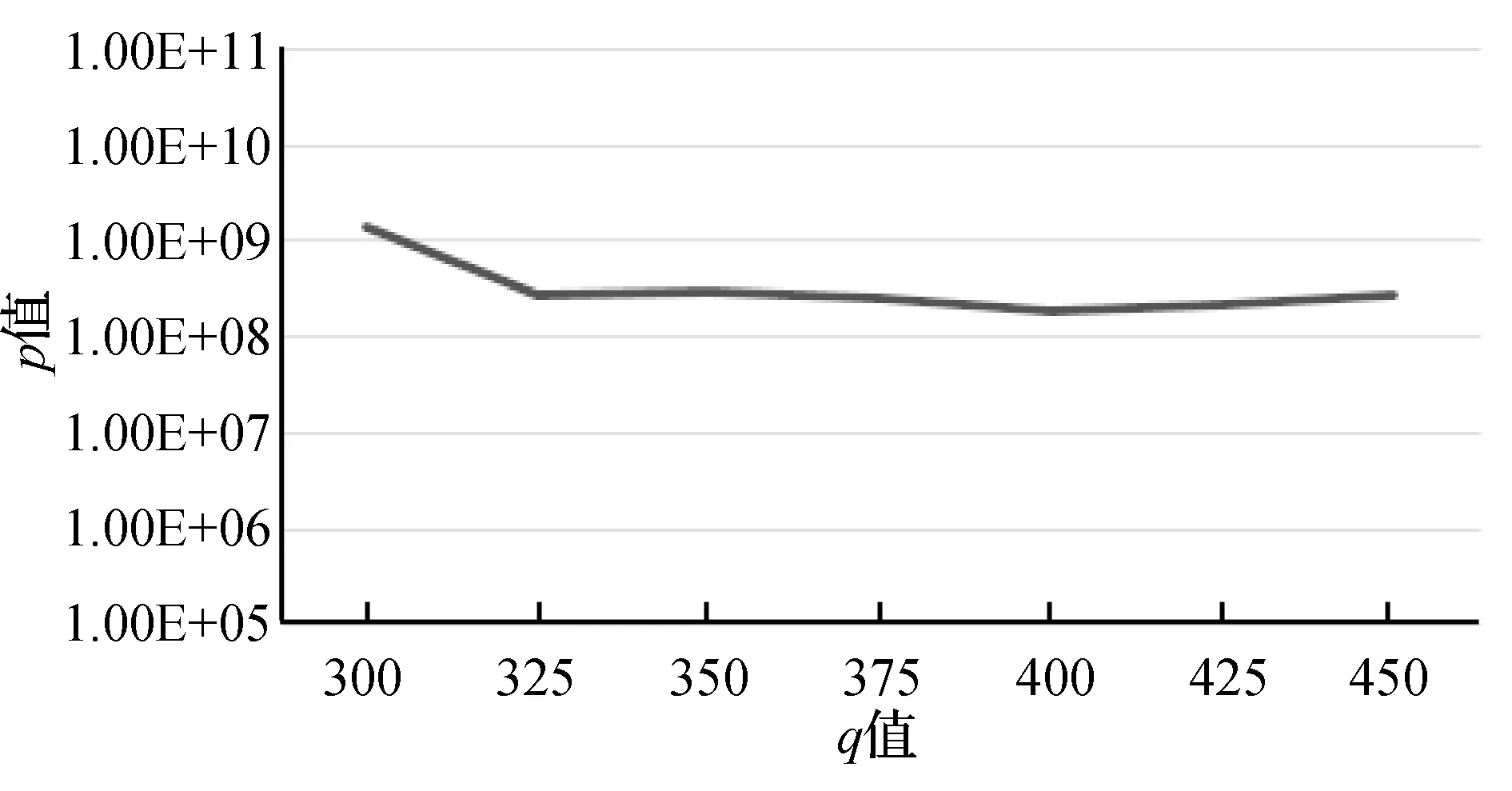
图6 KDD-CUP99数据集不同q值聚类效果对比图

图7 KDD-CUP99数据集不同K值聚类效果对比图

图8至图11分别是空气质量数据集对权重μ、衰变因数λ、初始聚类个数q和最终聚类簇个数K参数的聚类效果对比图。根据式(19)可知，p值越小越好，所以μ值、λ值、K值分别在区间 [1.5, 1.9]、[0.6,0.8]、[5,9]之间取值为佳，由于q值波动较大，所以在300、350、400、450这几个值中选择。综合实验得出，当μ=1.6，λ=0.6，q=400，K=6时聚类效果最好。

图8 空气质量数据集不同μ值聚类效果对比图

图9 空气质量数据集不同λ值聚类效果对比图

图10 空气质量数据集不同q值聚类效果对比图

图11 空气质量数据集不同K值聚类效果对比图

4.5 聚类质量验证

图12和图13分别反映了五种数据流聚类算法在KDD-CUP99数据集和空气质量数据集上的聚类质量。在KDD-CUP99数据集中，随着数据点增多，CluStream算法和DenStream算法的SSQ值小幅度上升，StrAP算法一直保持稳定的SSQ值，TEDA算法一开始维持较低的SSQ值，后来开始上升。PHAStream算法虽然处于小幅波动，但是总体还是比其他四类算法低1～3个数量级。

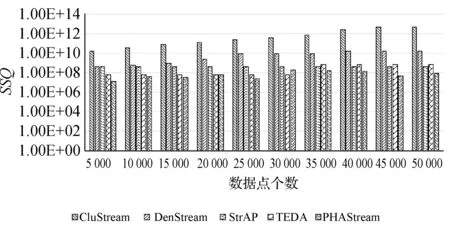
图12 KDD-CUP99数据集聚类质量对比图

图13 空气质量数据集聚类质量对比图

在空气质量数据集中，五种算法均保持稳定的SSQ值，并且PHAStream算法一直具有更低的SSQ值。因为SSQ值越低表示聚类质量越高，所以PHAStream算法具有更高的聚类质量。

4.6 聚类纯度验证

图14和图15分别反映了五种数据流聚类算法在KDD-CIP99数据集和空气质量数据集上的聚类纯度。在KDD-CUP99数据集中，随着数据点的增多，CluStream算法一开始保持较高的聚类纯度，之后一直处于较低的水平，因为噪点的增多，CluStream算法是以距离为相似度度量，且对所有数据点进行聚类，故聚类纯度不理想。DenStream算法和StrAP算法一直维持较高且较为稳定聚类纯度，TEDA算法总体维持较高的聚类纯度，PHAStream算法虽然在第20 000和第45 000个数据点时聚类纯度小幅降低，但是总体具有更好的聚类纯度。

图14 KDD-CUP99数据集聚类纯度对比图

图15 空气质量数据集聚类纯度对比图

在空气质量数据集中，CluStream算法和DenStream算法整个过程有小幅度波动，但是两者总体聚类纯度不高，StrAP算法聚类纯度较为稳定，TEDA算法一开始聚类纯度不高，但是随着数据点的增多，聚类纯度基本与StrAP算法持平，PHAStream算法相对其他四种算法一直具有更高的聚类纯度，这得益于势能场模型下，依据距离矩阵和势能共同作为相似度度量，故PHAStream算法具有更高的聚类纯度。

4.7 抗噪性验证

为了验证本文算法的抗噪性，将空气质量数据集进行适当修改，改为含有5%左右噪点的数据集，各算法在此数据集上进行实验，并求出所有统计时刻的平均值来进行前后对比。

由图16和图17可知，在加入5%左右的噪点后，CluStream算法在聚类质量和聚类纯度上相对其他几种算法变化较大，这是由于CluStream算法是以距离作为相似度度量标准，对噪点较为敏感，本文的PHAStream算法使用势能和距离来作为相似度度量标准，两者分别反映了数据点的全局与局部分布，减少噪点的干扰，具有更好的聚类效果。

图16 聚类质量对比图

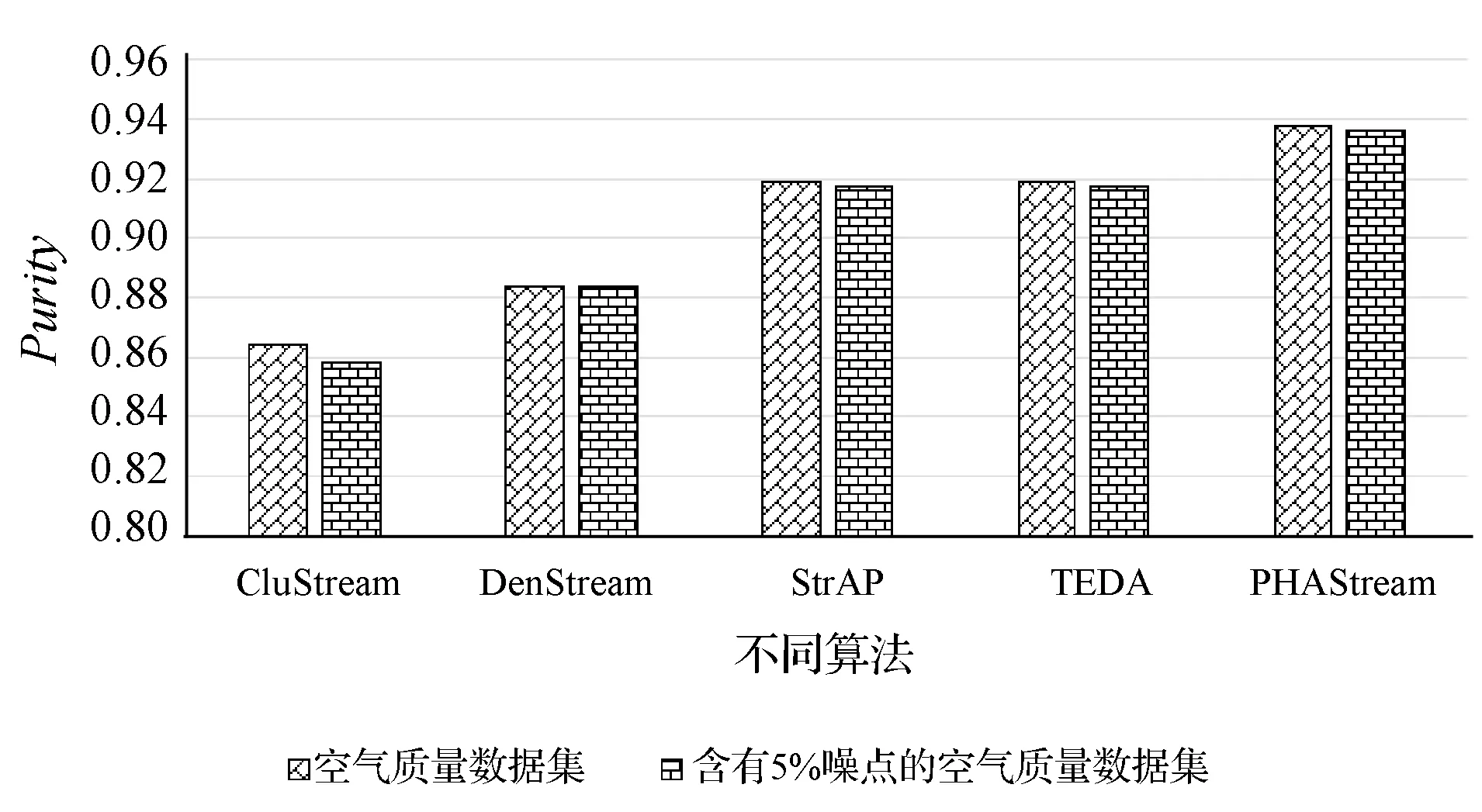
图17 聚类纯度对比图

4.8 时间效率验证

图18和图19分别反映了五种数据流聚类算法在KDD-CUP99数据集和空气质量数据集的执行时间对比图。PHAStream算法在整个阶段中均保持更低的时间消耗，这得益于新的概要数据结构中的dist_arr属性和边缘加权树技术，当有聚类要求时，可以快速构建距离矩阵，计算出势能，进而得到聚类结果。

图18 KDD-CUP99数据集时间效率对比图

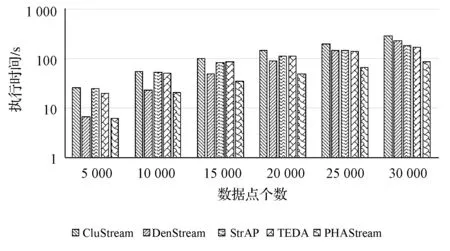
图19 空气质量数据集时间效率对比图

4.9 内存消耗验证

图20为五种数据流聚类算法在KDD-CUP99数据集和空气质量数据集的内存消耗对比图。PHAStream算法相对于其他四种算法均消耗更多的内存，这主要是因为其概要数据结构中的dist_arr属性，因为该属性存储了微簇之间的距离信息。PHAStream算法虽然消耗了更多的内存，但是在其他聚类效果上表现更优秀。

图20 时间效率对比图

5 结 语

本文提出一种基于势能模型的数据流聚类算法PHAStream，将基于势能模型的层次聚类算法PHA改造适用于数据流聚类。相对于大部分以距离为相似度度量的数据流聚类算法，本文的PHAStream算法以距离和势能作为相似度度量，这两者分别反映了所有数据点的局部和全局分布，减少噪点对聚类的干扰。实验结果表明，该算法可以有效提高聚类质量、聚类纯度和时间效率。

在本文的研究中，需要人工设置最终聚类簇个数。未来将考虑利用势能自动地确定聚类簇，使得该数据流聚类算法更高效。