一个格基无证书签密方案

欧海文 施 瑞 王佳琳

1(北京电子科技学院密码科学与技术系 北京 100070)2(西安电子科技大学通信工程学院 陕西 西安 710071)

0 引 言

签密是一个基本密码学原语[1]，它能同时满足加密和签名两种密码体制的安全性要求，即同时实现信息的保密性和不可伪造性。基于公钥基础设施(PKI)的签密体制证书管理较为复杂，基于身份的签密体制需考虑密钥托管问题，无证书密码体制[2]的提出解决了上述两种密码体制存在的缺陷。Farshim等[3]于2008年提出了第一个无证书签密方案，此后国内外研究者增加了对无证书签密体制的关注，并于近年来提出了多种无证书签密方案[4-9]。但现有的无证书签密方案的安全性均建立在传统数论假设的难解性之上，而随着量子计算的不断发展，促使我们不断去探索能够抗量子攻击的签密体制。

近年来迅速发展的格基密码体制能够有效地抵抗量子攻击，文献[10-11]均为已有的格基签密方案，而这些方案以格上的陷门生成算法和原像抽样算法为基础，计算开销较大。路秀华等[12]于2016年提出了一种无陷门格基签密方案，有效地改善格基密码体制中由于陷门生成算法和原像抽样算法而使得算法计算复杂的问题。2019年，Wang等[13]提出了无陷门格上基于身份的签密方案。文献[14-16]将格理论与无证书密码体制相联系，构造出格基无证书加密或签名方案。本文利用Galbraith等[17]提出的签名方案及路秀华等[12]的无陷门格基签密方案，结合无证书密码体制，提出了第一个格基无证书签密方案。

1 基础知识

1.1 符号说明

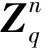
1.2 涉及的格中定义

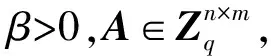
1.3 无证书签密方案及安全模型[18]

文献[18]详细地给出了无证书签密方案的形式化定义及其安全模型。其中，无证书签密方案的通信模型如图1所示。

图1 无证书签密方案的通信模型

其中，m为明文，σ为密文，IDi为用户i的身份信息，(PKi,Si)为用户i的公私钥对，(xi,Di)分别为用户i的秘密值信息及其部分私钥。

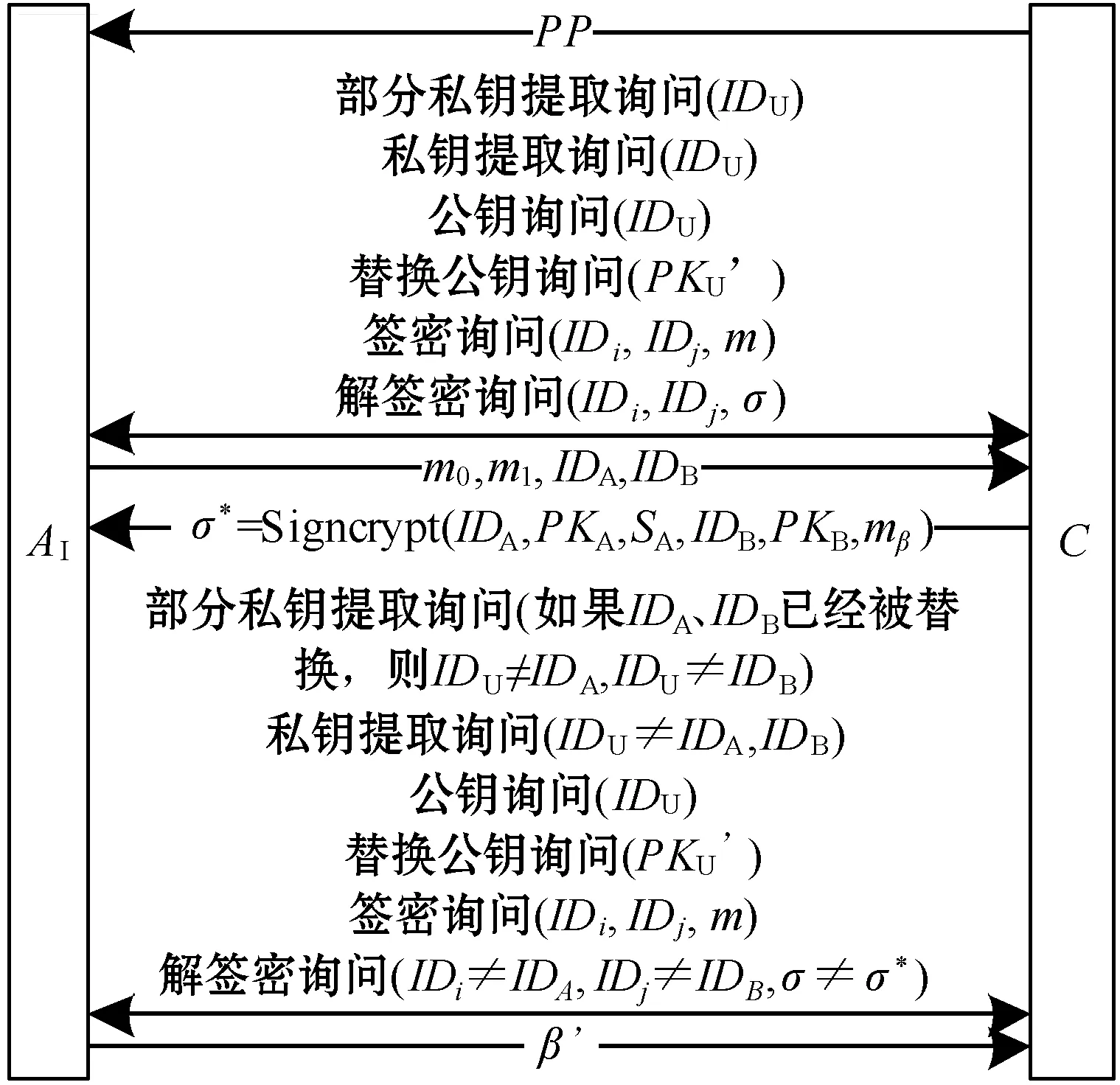
图2 类型I适应性选择密文攻击游戏

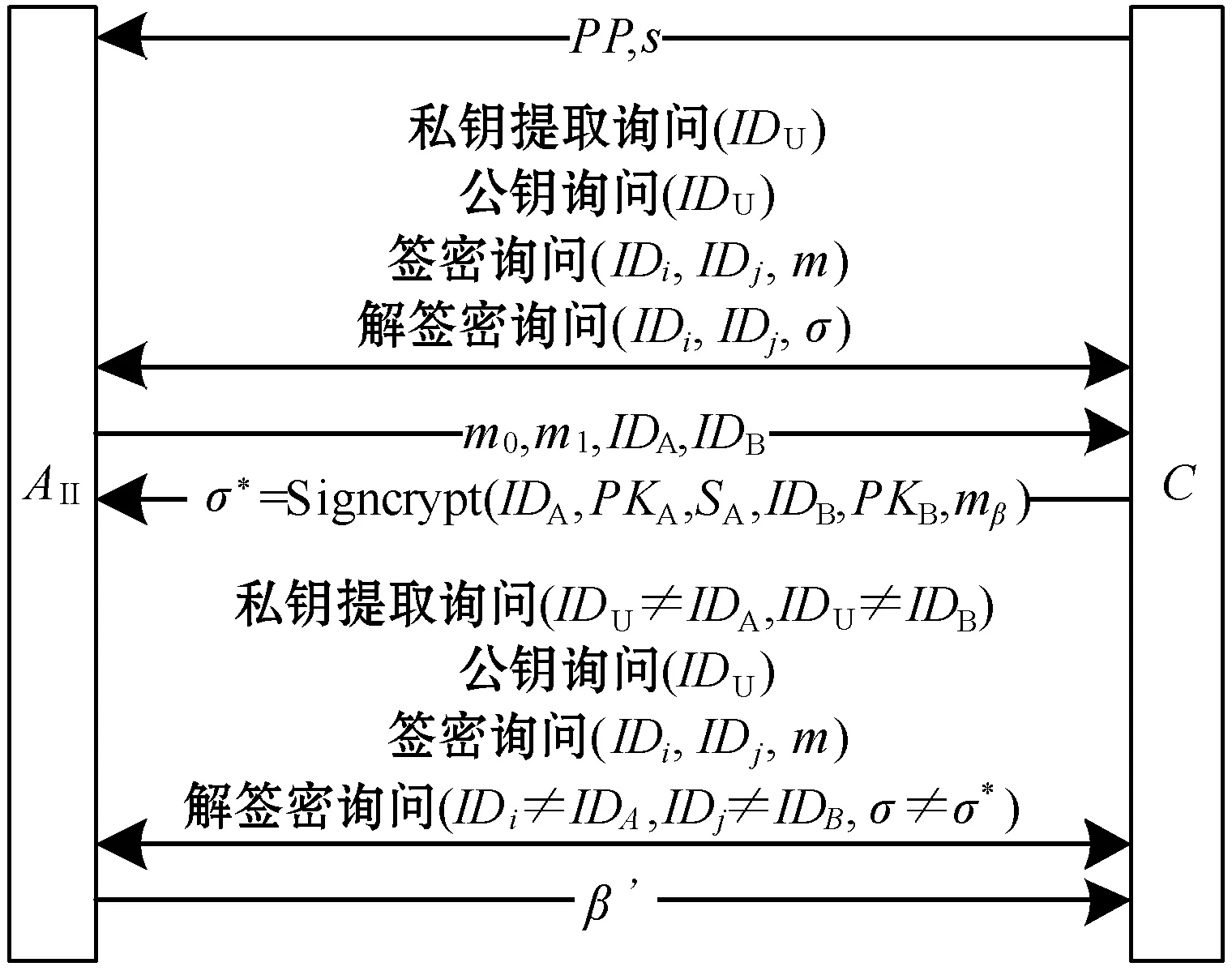
图3 类型II适应性选择密文攻击游戏

图4 类型I适应性选择消息攻击游戏

图5 类型II适应性选择消息攻击游戏

2 签密方案

2.1 系统建立：由KGC执行

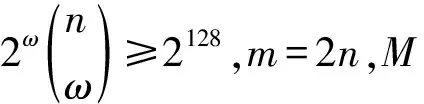
(2) 设置一个安全的理想对称加密算法(Ek,Dk)，其中k∈Σ。

(3) Hash函数：

H2:{0,1}n→Σ

H3:{0,1}*×{0,1}*→Π

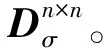
2.2 设置秘密值

2.3 部分私钥提取

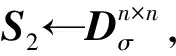
2.4 设置私钥

用户收到(T2,U2)后，首先验证A·U2=T0-T2(modq)是否成立。若成立，用户将U2作为部分私钥，计算全部私钥S=U2+S1。

2.5 设置公钥

用户计算自身公钥T=T0+T1-T2(modq)，并将其发送给KGC，KGC收到该公钥后将其作为该用户的公钥公布出来。

2.6 签 密

2.7 解签密

接收者收到密文C=(μ,v1,v2)，进行如下操作：

3 正确性分析

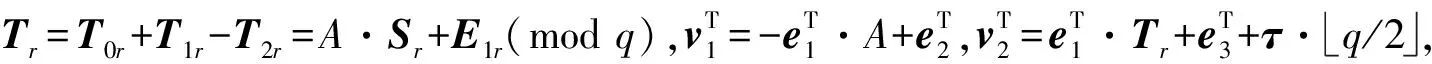
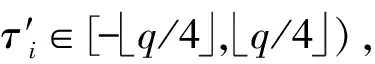
4 安全性分析

4.1 保密性

定理1在随机预言模型下，若判定性LWE问题是困难的，则该方案具有IND-CLSC-CCA2-I安全。

证明如果存在敌手I能够攻破上述方案的IND-CLSC-CCA安全，则挑战者可利用I的攻击解决判定性LWE问题实例(A,T*)，即能判定出T*来自下述两种情况：

① 服从均匀分布；

(1) H0询问。I输入(S2i,IDi,T1i)，随机抽取将h0返回给I，并将元组(S2i,IDi,T1i,h0)插入列表L0中。

(2) H2询问。I输入τi，随机抽取h2τi←Σ，令h2τi=H2(τi)，将(τi,h2τi)插入列表L2中，并将h2τi返回给I。

(3) H3询问。I输入(τi,μi)，随机抽取hτi,μi←Π，令hτi,μi=H3(τi,μi)，将(τi,μi,hτi,μi)插入L3列表中，并将hτi,μi返回给I。

① 若IDi=ID*，则Si=⊥，Ti=T0+T1i-T2i(modq)，然后把元组(IDi,(⊥,⊥),E1i,Ti)插入列表LID中，更新列表L0中的元组(S2i,IDi,T1i,h0)。

(9) H1询问。I输入(i,IDi)：查询列表LID获得IDi的公钥Ti，接着执行下述操作：

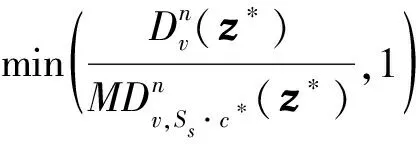
定理2若判定性LWE问题在随机预言模型下是困难的，则该方案具有IND-CLSC-CCA2-II安全。

证明该定理的证明过程类似于定理1的证明过程，通过敌手II与挑战者之间的互动游戏完成，具体如下：

H0、H1、H2、H3询问同定理1。

① 若IDi=ID*，则Si=⊥，计算T2i=A·h0i+E0，则Ti=T0+T1i-T2i(modq)，然后把元组(IDi,(⊥,⊥),E1i,Ti)插入列表LID中，更新列表L0中的元组(S2i,IDi,T1i,h0i)。

其余询问也同定理1一样。

4.2 不可伪造性

定理3若SIS问题在随机预言模型下是困难的，则该方案具有EUF-CLMS-CMA-I安全。

证明如果存在敌手I能够攻破上述方案的EUF-CLMS-CMA安全，则挑战者可利用I的攻击解决SIS问题实例即能找到非零向量e′∈Zn，e″∈Zm，使得Ae′+e″=0(modq)。挑战者和敌手I的具体交互过程如下所示：

1) 初始阶段。同定理1证明中的初始阶段一样。

定理4若SIS问题在随机预言模型下是困难的，则该方案具有EUF-CLMS-CMA-II安全。

证明该定理的证明过程类似于定理3的证明，通过敌手II和挑战者的互动游戏完成，具体如下：

1) 初始阶段。同定理2证明中的初始阶段一样。

5 性能及效率分析

本文方案与现有的无证书签密方案[4,8]相比，能够有效抵抗量子攻击。具体如表1所示。其中“Y”表示具有某种特性，“N”表示不具有某种特性。

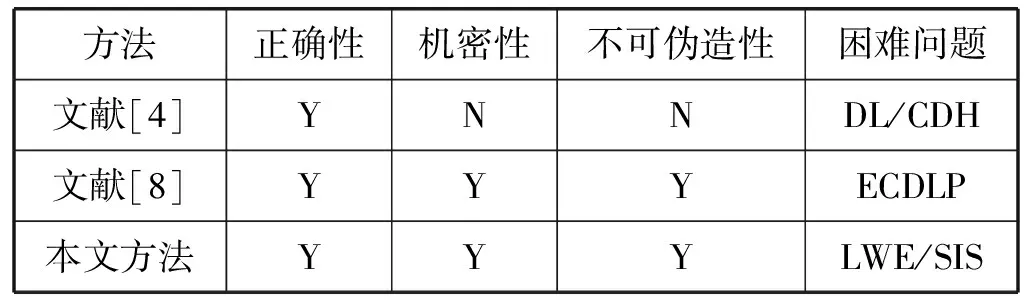
表1 方案性能分析表

本文方案与现有的格基无证书密码(签名/加密)方案[15-16]的密钥生成方式不同，不依赖于格基陷门生成算法，用到一个Hash函数，并进行了简单的矩阵线性运算，耗时较少。本文方案为第一个格基无证书签密方案，签密过程不依赖于原像抽样算法，运算效率较高。若忽略对称加密的运算量，则签密密文增量为2nlogq。若记Csample为进行高斯抽样时的运算量，Cm_mul为进行矩阵相乘时的运算量(忽略矩阵求和运算量)，则签/解签密运算量及密钥尺寸如表2所示。

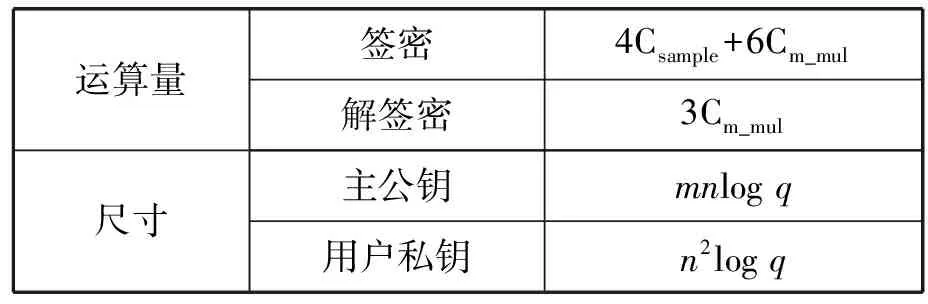
表2 本文方案运算量及公私钥尺寸表

6 结 语

结合格上签密方案和格基无陷门签名方案，本文提出了第一个基于格理论的无证书签密方案，在随机预言模型下对方案的正确性及安全性给予证明。本文提出的格基无证书签密体制是基本密码体制，而研究匿名多接收者签密、代理签密等特殊的格基无证书签密体制，是进一步研究的方向。