基于交替方向乘子算法的二维磁异常稀疏反演
罗重阳,张玉洁,2*
1 中国地质大学(武汉)数学与物理学院,武汉 430074 2 地质探测与评估教育部重点实验室,武汉 430074
0 引言
在地球物理勘探中,磁法勘探是以地壳中岩矿石等介质磁性差异为基础,通过观测磁场的变化规律来探查地质构造、寻找矿产等的一种物探方法(刘天佑,2007).它主要应用于研究区域地质构造、寻找磁铁矿、工程环境问题勘察等方面.在目前的磁法勘探中,磁异常物性反演是磁异常数据定量解释的有效手段和研究热点,它不仅能够描述目标地质体的几何和物理属性,还能对地质体的物性参数进行定量计算.但是,磁异常物性反演也存在着难以攻克的关键性问题:由于地下不同体积的场源会产生相同的磁异常,导致反演结果存在多解性问题.
为了解决反演结果的多解性这一关键问题,地球物理学家将正则化技术应用于反演中.简单来说,正则化技术是一种在模型解空间寻找特定解的方法,常常用于求解欠定性问题.对于磁异常反演或者其他地球物理场反演而言,一种非常经典的正则化技术是吉洪诺夫正则化(Tikhonov and Arsenin,1977),利用二次函数作为惩罚项加入到反演的目标函数中,从而求解出欠定问题的特定解.Li和Oldenburg(1996,1998)将吉洪诺夫正则化应用于重力异常与磁异常反演中,极小化模型的L2范数,以得到连续,光滑的反演结果.
为了获得聚焦和稀疏的反演模型,学者们将稀疏约束引入目标函数中.Last和Kubic(1983)将最小体积约束引入到重力数据反演中,提出了聚焦反演来恢复具有清晰密度边界的地下结构,其构建的范数被称为最小支撑泛函.这种方法被Portniaguine和Zhdanow(2002)进一步用于模型梯度的情况.Pilkington(2009)利用柯西范数证明了模型参数的稀疏性,对合成数据的测试表明,基于柯西范数的稀疏反演与最小二乘反演解相比,产生一个更加集中的效果.Meng等(2018)等建立了零范数反演目标函数,由于极小化零范数属于NP难问题,现有技术难以直接求解,他利用光滑函数序列对L0范数进行求解逼近求解(Mohimani et al.,2009)采用这种反演方法获得了具有清晰边界信息的结果.
近些年,随着压缩感知的飞速发展,压缩感知在各个领域发挥着越来越重要的作用,包括:图像重建(高雪,2015)、通信、地球物理(唐刚,2010;马坚伟,2018)等.压缩感知作为一种寻找欠定系统稀疏解的技术,近些年来被一些学者用于位场数据反演中.Vatankhah等(2017)讨论了基于L1范数正则化的重力数据稀疏反演,该方法在实际数据重建中,得到与已知信息基本一致的反演结果.Li等(2018)、李泽林等(2019)在Li和Oldenburg(2003)的基础上,将反演目标函数中模型的L2范数扩展为模型的Lp(0≤p≤1)范数,提出了物性上下界约束Lp(0≤p≤1)范数反演算法,获得了具有尖锐边界的反演结果,并进一步将这种方法应用于重力数据反演中.Utsugi(2019)在L1范数正则化的基础上,使用了L1-L2(即弹性网模型)混合正则化用于磁异常反演,这种方法克服了L1范数正则化得到过于集中的反演结果的缺点.
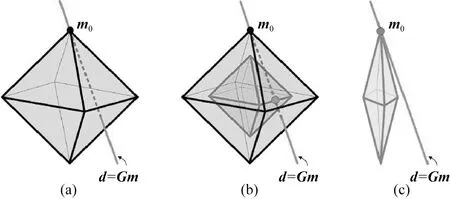
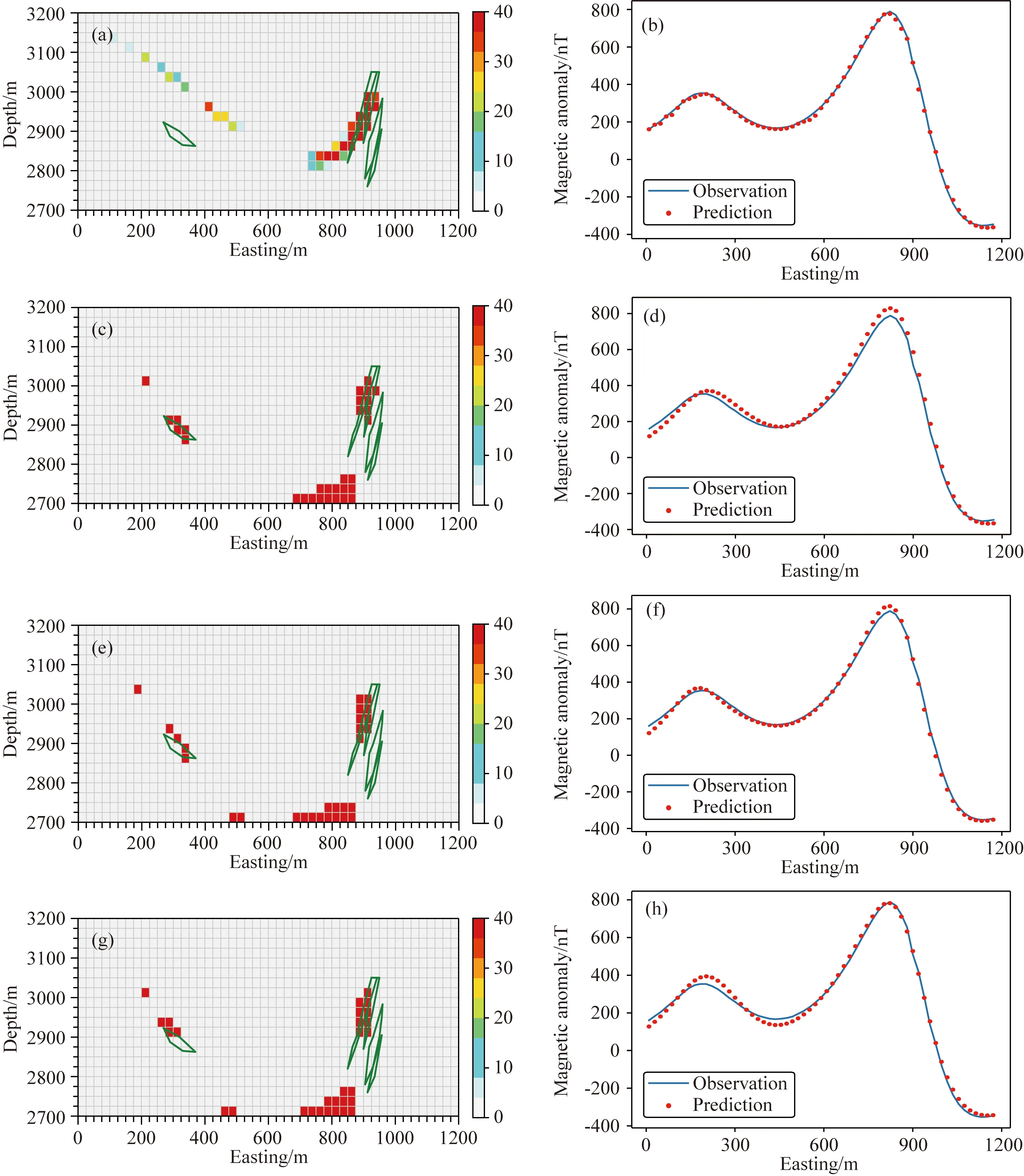
本文采用基于Lp(0 图1 磁异常反演网格剖分模型Fig.1 Mesh division model of magnetic anomaly inversion 如图1所示,将地下二维异常区域进行离散化处理,划分为多行多列的模型单元,每行每列模型单元都紧密相邻,每个模型单元大小形状一致,磁化率均匀;地表有一条横跨异常区域的测线,测线上均匀地分布着观测点.假设模型单元的总数为N,观测点的总数为M,则记第j个模型单元在第i观测点产生的磁异常为Δdij,公式为: Δdij=Gijmj, (1) 其中,mj表示第j的模型单元的磁化率,Gij表示第j个模型单元的单位磁化率在第i观测点产生的磁异常,利用磁异常正演公式(刘天佑,2007)对Gij进行定量计算,根据位场叠加性,第i个观测点的总磁异常等于场源区域所有模型单元在该观测点产生磁异常之和,记第i个观测点的总磁异常为di: (2) 将正演公式写为矩阵形式: d=Gm, (3) 其中,d=(d1,…,dM)为观测向量,G=(Gij)i=1,…,M ,j=1,…,N为核矩阵,m=(m1,…,mN)为模型磁化率向量. 在反演过程中,由于核函数会随着位场数据的深度而衰减,使得反演结果出现“趋肤效应”,即反演结果集中于地表,为了避免这种现象的产生,Li和Oldenburg(1998)提出了深度加权函数,对反演的物性参数进行加权,用来平衡不同深度的场源引起的场的衰减,其形式为: (4) 其中,W是一个对角矩阵,第i个对角元素为第i个模型单元的深度wi,β为参数,不同的β参数导致的反演结果不一样,Oldenburg和Li(2005)认为反演问题可以选择不同的β值进行尝试,最后选出最符合地质意义上的解,这种加权方式在各种反演算法中得到了广泛地应用. 地球反演的本质是求解一个欠定性问题,通过向量d和核矩阵G,求解向量m,由于N≫M,直接求解存在严重多解性问题.常用的方法是正则化技术,通过施加正则项来减少解的非唯一性. 针对式(3)的求解,利用正则化方法,构造反演目标函数: (5) (6) 通常根据反演的需求设置不同的正则项,根据正则项的构造,式(6)的优化问题可分为凸优化和非凸优化.在凸优化反演中,具有代表性的正则项是L2和L1正则项.基于L2正则化的目标函数处处可导,求解相对容易.其反演结果是光滑的,分辨率不高,常用的算法有梯度下降(Li and Oldenburg,2003;Pilkington,1997)等;基于L1正则化的目标函数在零点处不可导,求解难度相较L2正则化大幅提高.其反演结果是稀疏的,分辨率较高,常用的算法有坐标下降算法(Friedman et al.,2007),线性规划(Van Zon and Roy-Chowdhury,2006),稀疏梯度投影算法(Figueiredo et al.,2007),伯格曼算法(Dong et al.,2010)等.在非凸优化反演中,具有代表性的正则项是Lp(0 尽管前人在凸优化反演和非凸优化反演中展现了丰富的算法,但这些算法具有特异性,即不同的目标函数需要选择不同的算法进行求解,所以寻找一种适应性强的算法在反演中显得尤为必要.针对这个问题,本文将介绍ADMM算法在反演中的应用. ADMM算法最早分别由Glowinski和Marrocco(1975)及Gabay和Mercier(1976)年提出,近些年来,ADMM算法被重新整理和研究,并且证明其适用于大规模的分布式优化问题(Boyd et al.,2010).ADMM算法的核心思想是在原目标函数基础上,引入新的变量,将规模较大的目标函数分解为一系列规模较小的子问题求解,降低了求解难度,通过协调子问题的求解,从而获得原目标函数的全局解.考虑如下优化问题: minf(x)+g(x), (7) 其中,f、g为凸函数,变量x∈Rn.引入变量z∈Rn,将式(7)改写为: (8) 其中,变量z∈Rm,矩阵A∈Rn×n,矩阵B∈Rm×m以及向量c∈Rp.构造增广拉格朗日函数: L(x,z,y)=f(x)+g(z)+yT(Ax+Bz-c) (9) 其中,y∈Rn是拉格朗日乘子,ρ>0是惩罚因子. 算法的迭代过程为: (10) 令u=(1/ρ)y,上述迭代过程写成如下形式: (11) 上述过程表明,ADMM算法具有适应性很强的特点:凡具备式(7)结构,并且函数f、g为凸函数的目标函数优化问题,均可通过ADMM算法进行求解,并且可以保证其收敛性.这就为后续研究不同的反演目标函数提供了通用算法.当函数f、g中至少一个为非凸函数时,ADMM算法可以视为一种局部优化算法,其最终结果与起始点和参数有关.本文将从凸优化反演中的L1正则化和非凸优化中的Lp(0 当目标函数的正则项为L1范数时,利用ADMM算法框架将式(6)改写为: (12) 进一步,将式(11)转化为极小化一系列子问题进行求解,迭代步骤: (13) 原问题为: (14) 属于凸优化问题,对变量mw求导,并使其等于零,得到如下等式: (15) (16) 由于矩阵Gw维度比较大,式(15)直接求逆效率比较低,为了提升(15)的求解效率,采用预处理共轭梯度法(Preconditioned Conjugate Gradient,PCG),PCG算法的有优点在于收敛快,计算过程中不用存储矩阵,在重磁反演中得到广泛应用(Pilkington,2009;陈召曦等,2012).在每次迭代求解后对参数进行阈值处理,将参数限制在一定范围.参数的约束对反演而言具有重要意义,一方面能使得参数分布在期望范围内,更重要的是可以提高反演的分辨率(Sun and Li,2016).参数的约束采用上下界约束(Meng et al.,2018;Portniaguine and Zhdanov,2002;赵洋洋等,2022),形式为: (17) 其中,0和bi分别为反演参数的上下界. (2)zk+1的求解 原问题为: (18) 根据式(18)可以看出,向量z的每一个分量都可以独立求解,只需对向量z的分量zi(i=1…N)进行优化求解,优化问题写为: (19) (20) 继而对解析解进行阈值处理: (21) 一方面,从反演目标函数(12)的约束条件来看,变量mw和z是相等的,没有必要对其都进行阈值处理;另一方面,从目标函数的正则项来看,求解mw时候是极小化L2范数,L2范数特点是对mw的每个分量给与本身的权重,即较大的分量具有较大权重,较小的分量具有较小的权重,这就使得最终求解的值往中间范围靠拢,不容易出现越界值;反观z的求解是极小化L1范数,L1范数的特点是对z的每个分量给与相同的权重,这就使得求解允许出现较大值和较小值,所以需要对最终的求解结果进行阈值处理.因此,在算法设计中,仅对变量z进行阈值处理.具体算法如下: 算法1:基于L1正则化的ADMM反演算法输入:核矩阵Gw,磁异常向量d,正则化参数λ,惩罚因子ρ,深度加权矩阵W.输出:模型参数向量m∗.初始化:m0w=0,z0=0,u0=0.循环:k=k+1;1.利用PCG算法求解(15),更新mk+1w;2.利用(20)和(21)更新zk+1;3.更新uk+1;直到收敛.5.更新模型参数m∗=W-1zk+1. 当目标函数为Lp(0 当0 (22) 同理,对向量z的分量zi(i=1,…,N) 进行优化求解,化简: (23) 针对式(23)非凸优化子问题的求解,前人做了许多工作,例如:利用凸松弛技术求解,代表算法有迭代重加权最小二乘(Chartrand and Yin,2008;Daubechies et al.,2010),迭代重加权L1(Candès et al.,2008)等,此类算法会使得式(23)的求解收敛到局部极小值,子问题的求解不精确将会进一步影响ADMM算法在非凸问题的求解,用在此处显然不合适,所以该子问题的求解应该采用能够收敛到全局极小值的算法. 当ρ/2=1时,对于式(23)的全局极小值的求解,Zuo等(2013)在软阈值函数基础上提出了广义软阈值算法,具体算法如下: 算法2:广义软阈值(GST)算法输入:si,λ,p,J.输出:TGSTp(si;λ).1.计算τGSTp(λ)=(2λ(1-p))1/(2-p)+λp(2λ(1-p))(p-1)/(2-p);2.如果si<τGSTp(λ),则TGSTp(si;λ)=0;3.否则,令k=0,zk=si;循环k=0,1,…,J;zk+1i=si-λp(zk)p-1;k=k+1;TGSTp(si;λ)=sgn(si)zk;结束. 利用此方法,从而得到优化式(23)的解: (24) 同式(21),在每次迭代后的结果进行阈值处理: (25) 其中,0和bi分别为反演参数的上下界.具体算法如下: 算法3:基于Lp(0 为了验证本文提出的算法的有效性,我们采用了磁异常反演中常用的三种二维模型进行模拟实验,同时,与传统的基于L2范数的反演方法(Li and Oldenburg,2003)进行了对比. 三种模型分别为直立板状体模型、倾斜板状体模型以及向斜模型.首先将地下区域进行离散化处理,剖分为20行40列,一共800个形状大小相同的网格模型单元,每个模型单元是边长为25 m的正方形,并且每个模型体单元认为是均匀磁化的,磁化强度为100 A·m-1,磁化倾角为I=45°,测线磁方位角为A=0°,即有效磁化角为45°,观测点个数设置为51. 图2、图3、图4是三种不同模型分别用本文提出基于的Lp范数(其中p分别取1,0.7,0.4,0.1)以及L2范数的反演结果,在这些图中,加粗框线的位置代表场源的真实位置,颜色深浅代表每个模型单元的磁化率的大小. 从图2—图4中的模拟实验可以看出,本文提出的基于ADMM算法的L1范数和Lp(0 针对基于Lp(0 (26) 为了进一步评价本文算法的精度,利用L1范数定义了反演结果的相对误差,用E来表示: (27) 其中,m代表原始结果,m*代表反演结果.每个模型的反演相对误差见表1. 表1 反演相对误差Table 1 Relative error of inversion 从表1中可以发现,在直立板状体模型和向斜模型中,基于Lp(p=0.4,p=0.1)范数反演效果优于基于L1范数反演,而基于Lp(p=0.7)范数反演与基于L1范数的反演效果相当;在倾斜板状体模型中,基于L1范数反演与基于Lp(p=0.7,p=0.4,p=0.1)范数反演效果相当;在向斜模型中,基于Lp(p=0.7,p=0.4,p=0.1)范数反演效果均优于基于L1范数反演;此外,在这三种模型中,本文的两种算法都远远优于基于L2范数反演算法效果. 图2 直立板状体模型反演结果(a) L1范数反演结果;(b) L1范数反演数据拟合;(c) Lp(p=0.7)范数反演结果;(d) Lp(p=0.7)范数反演数据拟合;(e) Lp(p=0.4)范数反演结果;(f) Lp(p=0.4)范数反演数据拟合;(g) Lp(p=0.1)范数反演结果;(h) Lp(p=0.1)范数反演数据拟合;(i) L2范数反演结果;(j) L2范数反演数据拟合.Fig.2 Inversion results of vertical plate model(a) L1 norm inversion results;(b) L1 norm inversion data fitting;(c) Lp(p=0.7) norm inversion results;(d) Lp(p=0.7) norm inversion data fitting;(e) Lp(p=0.4) norm inversion results;(f) Lp(p=0.4) norm inversion data fitting;(g) Lp(p=0.1) norm inversion results;(h) Lp(p=0.7) norm inversion results;(i) L2 norm inversion results;(j) L2 norm inversion data fitting. 图3 倾斜板状体模型反演结果(a) L1范数反演结果;(b) L1范数反演数据拟合;(c) Lp(p=0.7)范数反演结果;(d) Lp(p=0.7)范数反演数据拟合;(e) Lp(p=0.4)范数反演结果;(f) Lp(p=0.4)范数反演数据拟合;(g) Lp(p=0.1)范数反演结果;(h) Lp(p=0.1)范数反演数据拟合;(i) L2范数反演结果;(j) L2范数反演数据拟合.Fig.3 Inversion results of inclined plate model(a) L1 norm inversion results;(b) L1 norm inversion data fitting;(c) Lp(p=0.7) norm inversion results;(d) Lp(p=0.7) norm inversion data fitting;(e) Lp(p=0.4) norm inversion results;(f) Lp(p=0.4) norm inversion data fitting;(g) Lp(p=0.1) norm inversion results;(h) Lp(p=0.7) norm inversion results;(i) L2 norm inversion results;(j) L2 norm inversion data fitting. 图4 向斜模型反演结果(a) L1范数反演结果;(b) L1范数反演数据拟合;(c) Lp(p=0.7)范数反演结果;(d)Lp(p=0.7)范数反演数据拟合;(e) Lp(p=0.4)范数反演结果;(f) Lp(p=0.4)范数反演数据拟合;(g) Lp(p=0.1)范数反演结果;(h) Lp(p=0.1)范数反演数据拟合;(i) L2范数反演结果;(j) L2范数反演数据拟合.Fig.4 Inversion results of synclinal model(a) L1 norm inversion results;(b) L1 norm inversion data fitting;(c) Lp(p=0.7) norm inversion results;(d) Lp(p=0.7) norm inversion data fitting;(e) Lp(p=0.4) norm inversion results;(f) Lp(p=0.4) norm inversion data fitting;(g) Lp(p=0.1) norm inversion results;(h) Lp(p=0.7) norm inversion results;(i) L2 norm inversion results;(j) L2 norm inversion data fitting. 结合上述的表现说明ADMM算法可以应用于凸优化反演和非凸优化反演中. 图5 极小化加权L1增强稀疏性(a) 稀疏向量m0,可行域d=Gm,和半径为‖m0‖的范数球;(b) 存在m≠m0,使得‖m‖<‖m0‖;(c) 加权L1球,不存在m≠m0,使得‖Wm‖≤‖Wm0‖.Fig.5 Weighted L1 minimization to enhanced sparsity(a) Sparse vector m0,feasible set d=Gm,and L1 ball of radius‖m0‖;(b) There exists an m≠m0 for which ‖m‖<‖m0‖;(c) Weighted L1 ball,There exists no m≠m0 for which ‖Wm‖≤‖Wm0‖. 为了讨论ADMM算法在反演中的性能,以模拟实验中直立板状体模型为例分ADMM算法反演的精度(以模型的相对误差来衡量)与迭代次数的关系. 从图6中可以看出,对于一个固定的正则化参数,ADMM算法前期迭代过程中收敛较快,后期迭代过程中收敛较慢,反演精度要求很高的情况下,需要大量的迭代,反演精度要求不高的情况下,该算法可以以较少的迭代次数达到要求.同时,由于Lp(p=0.1)范数反演是非凸问题,较L1范数反演更复杂,并且,在求解过程中联合了广义软阈值算法,使得过程更复杂,所以收敛速度更慢. 实际数据采用从青海省尕林格铁矿保护区获取的剖面磁异常数据,用本文方法对矿区两条沿测线的剖面数据进行反演,测线图7是青海省尕林格矿区磁异常平面等值线图,该地区的主磁铁矿被大面积的沙砾层围岩所覆盖,磁异常的最大值为1600 nT,磁铁矿的平均磁化强度为40 A·m-1.对于该地区的磁异常反演,前人已经做了许多工作(刘双等,2012;Liu et al.,2014,2018).212和196为两条平行的穿过主要的矿体暴露区域的测线,每条测线1200 m,分别有61个观测点,矿体区域划为为20行48列的模型单元,每个模型单元为边长25 m的正方形. 图6 ADMM算法迭代误差图(a) L1范数反演迭代过程;(b) Lp(p=0.1)范数反演迭代过程.Fig.6 Iteration error diagram of ADMM algorithm(a) L1 norm inversion iterative process;(b) Lp(p=0.1) norm inversion iterative process. 图7 青海省尕林格矿区磁异常平面等值线图(Liu et al.,2014)Fig.7 Plane contour map of magnetic anomaly in Galinge mining area,Qinghai province(Liu et al.,2014) 在图8和图9中,加粗框线的位置代表场源的真实位置,颜色深浅代表每个模型单元的磁化率的大小.针对真实数据,本文的两种算法均能大致反映出场源的位置和走向,同时,物性参数均分布在合理范围内,数值大小符合实际.不同之处在于基于L1范数的反演异常曲线的拟合程度较高;基于Lp(0 图8 196测线反演结果(a) L1范数反演结果;(b) L1范数反演数据拟合;(c) Lp(p=0.7)范数反演结果;(d) Lp(p=0.7)范数反演数据拟合;(e) Lp(p=0.4)范数反演结果;(f)Lp(p=0.4)范数反演数据拟合;(g) Lp(p=0.1)范数反演结果;(h) Lp(p=0.1)范数反演数据拟合.Fig.8 Inversion results of 196 survey line(a) L1 norm inversion results;(b) L1 norm inversion data fitting;(c) Lp(p=0.7) norm inversion results;(d) Lp(p=0.7) norm inversion data fitting;(e) Lp(p=0.4) norm inversion results;(f) Lp(p=0.4) norm inversion data fitting;(g) Lp(p=0.1) norm inversion data fitting;(h) Lp(p=0.1) norm inversion data fitting. 图9 212测线反演结果(a) L1范数反演结果;(b) L1范数反演数据拟合;(c) Lp(p=0.7)范数反演结果;(d) Lp(p=0.7)范数反演数据拟合;(e) Lp(p=0.4)范数反演结果;(f) Lp(p=0.4)范数反演数据拟合;(g) Lp(p=0.1)范数反演结果;(h) Lp(p=0.1)范数反演数据拟合.Fig.9 Inversion results of 212 survey line(a) L1 norm inversion results;(b) L1 norm inversion data fitting;(c) Lp(p=0.7) norm inversion results;(d) Lp(p=0.7) norm inversion data fitting;(e) Lp(p=0.4) norm inversion results;(f) Lp(p=0.4) norm inversion data fitting;(g) Lp(p=0.1) norm inversion data fitting;(h) Lp(p=0.1) norm inversion data fitting. 在196测线中,Lp(0 针对基于Lp(0 (2) 在反演过程中,当正则化参数较大时,正则项的权重相对较大,一方面会导致目标函数的误差项过大,另一方面,会使得反演结果的模型单元呈现二值性(即0和40),但是模型单元的实际情况并非全部是均匀的,可能会导致拟合曲线局部的变化;当正则化参数较小的时候,目标函数的误差平方项的权重相对较大,正则项的影响较小,目标函数误差项较小,同时,反演结果也具备稀疏性,不会呈现出二值性的特点. ADMM算法在近几年受到了较高的关注度,其主要原因除了上文提到的可以分离凸问题,降低目标函数的求解难度之外,另外一个原因是是可用于解决大规模优化问题. 考虑式(6)的一般化的反演问题,当核矩阵Gw过大时,改写为: (28) 其中,gi是核矩阵Gw中的第i行,di是磁异常向量d的第i个.将数据空间进行分割,引入局部引入局部变量(mw)i∈Rn和全局变量z,将式(28)改写为: (29) 式(28)被称为一致性优化问题,利用ADMM算法将式(29)改写为一系列子问题进行求解(Boyd et al.,2010),每一个局部变量(mw)i可以单独求解,结合并行计算的技术,使局部变量(mw)i的求解同时进行,从而达到处理大规模问题的能力. 本文利用ADMM算法框架,将比较难求解的主问题分解为一系列相对容易求解的子问题,同时,每个子问题给出了相应的求解步骤.为了验证算法的有效性,分别进行了模拟实验和真实数据实验.模拟实验表明,本文算法均能够较好的反映出异常场源的形状和位置以及物性参数的大小,其中,基于Lp(0 磁异常反演除了面临多解性问题之外,另一个需要解决大规模数据反演.传统反演算法属于串行计算,计算能力有限,面对大规模问题难以求解,而ADMM算法具有分布式特点,能使算法并行化求解,达到处理大规模问题的能力,并在其他的方面已经成功应用,例如:高维数据变量选择(Wang et al.,2018),这也为今后大规模重磁反演提供了新思路.下一步计划将结合分布式计算原理,实现并行计算,从而在保证反演精度的情况下,解决大规模反演问题.
1 正演问题
2 深度加权

3 反演
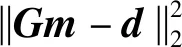
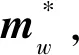
3.1 ADMM算法

3.2 基于ADMM算法的凸优化反演
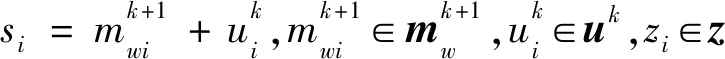

3.3 基于ADMM算法的非凸优化反演




4 实验
4.1 二维模拟实验
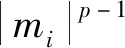






4.2 二维真实数据实验



5 展望
6 结论

