拟空间域弹性波方程交错网格有限差分逆时偏移

张晓波，宋鹏，刘保华，谭军，李金山

1 山东科技大学，海洋科学与工程学院，青岛 266590 2 青岛海洋科学与技术国家实验室，海洋地质过程与环境功能实验室，青岛 266061 3 中国海洋大学，海洋地球科学学院，青岛 266100 4 自然资源部，国家深海基地管理中心，青岛 266237

0 引言

地震勘探是目前探测复杂地下地质构造最重要的地球物理方法之一，主要包括地震信息采集、数据处理和成像解释三大环节（Yilmaz,2001）.而地震数据处理是连接信息采集与成像解释环节的重要桥梁.长期以来，精确的地下构造偏移成像一直是地震数据处理中的研究热点（Guo et al.,2002；Chattopadhyay and McMechan,2008）.

基于双程波动方程理论进行逆时偏移成像是当前公认的精确构造成像方法（Mora,1987;Sun and McMechan,2001;Sirgue et al.,2010;Plessix and Perkins,2010;王保利等,2012;Moradpouri et al.,2017）.逆时偏移（Reverse Time Migration,RTM）算法出现于20世纪80年代早期（Whitmore,1983;McMechan,1983;Chang and McMechan,1987,1990,1994），其不需要对波动方程进行分解，避免了因对波动方程近似而造成的倾角限制，因此该方法能够适用于复杂构造成像，一直以来都是偏移成像领域的重要研究内容（Clapp,2009;刘红伟等,2010;刘欣欣等,2013;石颖等,2015;宋鹏等,2015;李庆洋等,2017;Li et al.,2018,2020）.

近年来，国内外地震勘探技术发展迅速，特别是多波多分量地震数据采集技术已日渐成熟并且在实际油气勘探中取得了良好的应用效果，值得大力推广（张树林和张懿,2014）.为了充分利用多波多分量地震数据中丰富的纵、横波信息，实现地下构造精确成像，大力发展弹性波方程逆时偏移已势在必行.目前一些学者已开展相关研究工作，如：Chang和McMechan首先将二维逆时偏移推广到弹性波领域（Chang and McMechan,1987），随后又将其推广至三维情况（Chang and McMechan,1990,1994）；Luo 等（2013）利用谱元法和基于伴随矩阵的成像条件实现了弹性波逆时偏移；王玉凤（2014）基于SEG/EAGE模型实现了多波多分量数据弹性波方程逆时偏移；Duan和Sava（2017）实现了弹性波方程逆时偏移成像道集的角度域分解；Du等（2014）和Gong等（2018）分别基于不同的纵横波分量实现了弹性波逆时偏移成像；Zhang和Shi（2019）研究了弹性波逆时偏移的成像条件；Qu 等（2020）为解决常规纵横波波场分离方法存在的PS和SP分量动力学特性改变以及极性反转等问题，提出了一种基于曲线坐标的OBC数据波场分离弹性逆时偏移方法.

随着研究的不断深入，弹性波方程逆时偏移方法已日趋完善，然而在当前的实现和应用过程中，其仍存在以下两个方面的问题有待进一步研究.首先，波动方程有限差分逆时偏移技术在当前的实现中均普遍应用到重要的数值计算方法——有限差分法（Bartolo et al.,2017;Ren and Li,2017；赵明哲等,2022）.众所周知，传统的波动方程有限差分计算方法本身存在着难以克服的固有问题——空间域的矩形网格剖分必然造成地震速度界面的畸变（刘立彬等,2020）.图1给出了一个包含倾斜速度界面模型的常规有限差分法网格剖分示意图.图中黑色实线为倾斜速度界面，而红色实心点和蓝色实心点分别表示界面两侧的速度.显然，矩形网格剖分的结果使得原本光滑的倾斜速度界面畸变为明显的阶梯状折线，当地震波传播至这样的界面时会形成一系列的假散射（褚春雷和王修田,2005）；此外地震波在遇到速度分界面时会产生大量的层间反射波，其在偏移剖面上形成较强的低波数干扰，其会严重影响剖面的信噪比并可产生偏移假象（Liu et al.,2011a），从而影响偏移剖面的精度.这两个问题的有效解决对提高逆时偏移的成像质量具有重要意义.

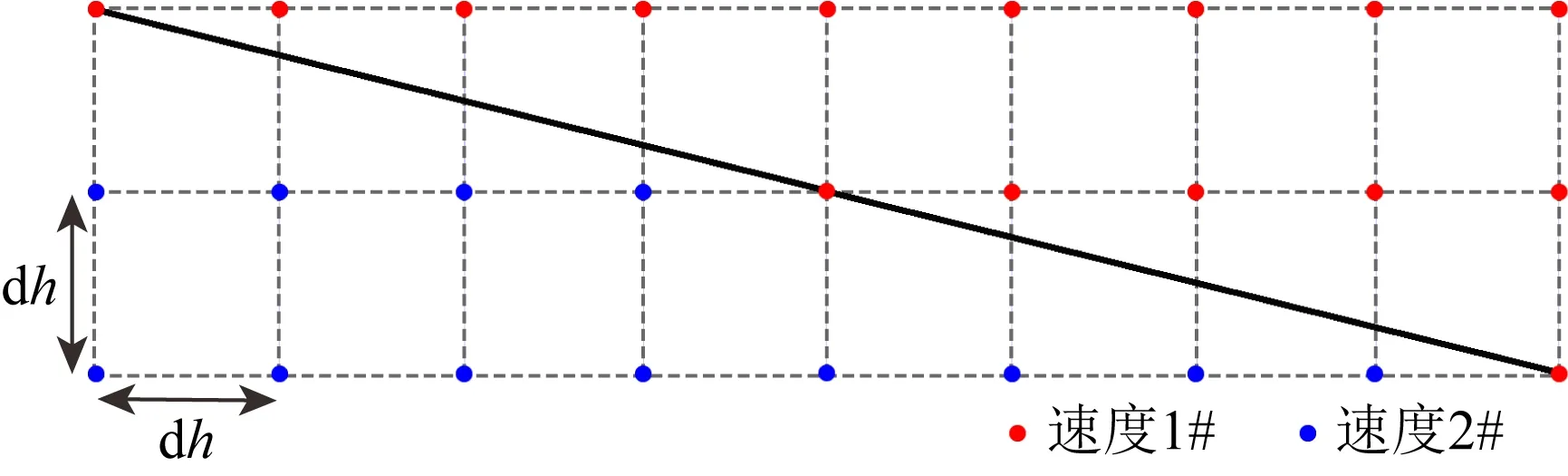
图1 常规有限差分法网格剖分示意图Fig.1 Schematic diagram of regular meshing in conventional finite difference method

为了消除逆时偏移过程中的假散射和界面畸变的现象，一些学者采用空间可变网格（朱生旺和魏修成,2005；朱生旺等,2007;黄超和董良国,2009；姜占东等,2021）的思路，在介质变化剧烈的区域采用精细网格，在介质变化平缓的区域采用较粗网格剖分，但该方法仍没有摆脱矩形网格的局限性；褚春雷和王修田（2005）根据有限元的思想采用基于非规则三角形网格的有限差分方法实现有限差分模拟，该方法可以更精细地描述起伏界面，但是其计算量与传统矩形网格有限差分相比明显增加.

而对于由于层间反射波引起的低波数噪声干扰压制问题，当前主要有如下几类方法：第一类是背向反射压制方法，其通常是基于能够弱化反射波场的波动方程进行波场延拓，以达到压制层间反射波、减弱低波数干扰的目的.Baysal等（1984）首先提出了基于常波阻抗假设的无反射声波方程，可显著压制垂向附近入射的地震波背向反射；宋鹏（2005）和Zhang 等（2010）改进了无反射声波方程，提升了背向反射的压制效果.第二类方法为滤波类方法，如高通滤波、拉普拉斯滤波等.Mulder和Plessix（2004）直接采用高通滤波方法对成像剖面进行去噪处理；Zhang和Sun（2009）采用Laplacian滤波方法对常规逆时偏移结果进行滤波.第三类是行波分离方法，该方法对震源波场和检波点波场分离成不同方向的行波，然后提取有效波场分量参与成像，从而实现地下构造的精确成像.Liu 等（2011a）首先基于F-K变换实现了波场分离逆时偏移成像，有效地压制了偏移噪声；Fei等（2015）、王一博等（2016）应用Hilbert变换实现了行波分离的逆时偏移成像；Chen和He（2014）采用Poynting矢量实现了震源波场与检波点波场上、下、左、右四个方向的行波分离，有效提高低波数噪声的压制效果.以上三类方法各有优劣，相对而言，背向反射压制与波场分离这两类方法是在成像过程中压制低波数噪声，其对于最终成像质量的提高更为有效，对于这二者来讲，背向反射压制方法更具计算效率优势；而滤波类方法虽可有效压制低波数噪声，但该类方法是在成像计算之后压制低波数噪声，对于复杂构造模型其成像剖面的精度往往受到一定影响，且该类方法还存在滤波器阈值范围选择困难，易损伤有效信息，有时还会引入大量高频噪声（陈康和吴国忱,2012）等问题，因此该类方法在实际数据处理时需谨慎使用，或与其他类方法搭配使用以期达到更优的成像效果.

2005年SEG年会上，Wang 等（2005）通过将传统的波动方程从时间-空间域变换到时间-走时域（或称作“走时域”），推导出了一种拟空间域声波方程，其既可有效解决常规波动方程逆时偏移中的弯曲界面假散射和界面畸变的问题，同时像无反射声波方程类似，该方程还可显著减少波场延拓中的背向反射，达到压制成像剖面中的低波数噪声，提高成像质量的目的.但Wang等（2005）仅实现了基于拟空间域二阶差分精度有限差分模拟，其模拟精度较低，限制了该方法在实际中的应用.本文在详细讨论拟空间域弹性波方程原理的基础上，推导了任意偶数阶拟空间域一阶速度-应力弹性波方程交错网格有限差分格式，并给出了其稳定性条件，实现了高精度的拟空间域一阶速度-应力弹性波方程交错网格有限差分逆时偏移.

1 拟空间域一阶速度-应力弹性波方程

在二维各向同性介质中，拉梅常数λ和μ与介质纵波速度vp、横波速度vs以及密度ρ之间满足关系：

（1）

根据式（1）和常规一阶速度-应力弹性波方程（Virieux,1986;Coutant et al.,1995;Liu and Sen,2011b），二维各向同性弹性波方程可表示成：

（2）

其中，x、z分别代表空间的横向坐标和纵向坐标，σp表示应力波场的纵波分量，σxxs表示水平方向上正应力的横波分量，σzzs表示垂直方向上正应力的横波分量，σxz表示切应力波场，vx表示水平速度分量波场，vz表示垂直速度分量波场，s（t）为震源函数，t表示时间.

图2 空间模型离散化之后的差分网格划分示意图Fig.2 Illustration of the spatial model after discretization

当基于式（2）所示的弹性波方程进行有限差分波场延拓时，将时间和空间离散化后（如图2所示），令i和j分别代表x和z方向上网格点坐标.假设空间无限小的网格长度为Δξ（ξ可以代表x或z），地震波在该网格上纵横波走时分别为Δτ（p）ξ和Δτ（s）ξ，则空间网格Δξ与走时Δτ（p）ξ和Δτ（s）ξ之间满足关系式：

（3）

根据式（3）可以将应力σ（σ代表σp,σxxs,σzzs或σxz）以及速度分量vx、vz对空间的导数变换为：

（4）

然后将式（4）代入式（2）中可得：

（5）

式（5）即为拟空间域一阶速度-应力弹性波方程.

2 拟空间域一阶速度-应力弹性波方程数值计算

2.1 拟空间域采样间隔计算

通常情况下，为了采用有限差分方法描述拟空间域弹性波方程（如式（5）所示），首先要按照传统的有限差分方法将连续的空间模型变成离散化的空间网格模型，然后在每个空间网格线Δξ上，根据其对应的网格速度值计算纵横波走时Δτ（p）ξ和Δτ（s）ξ.为了便于描述，本节中将Δτ（p）ξ和Δτ（s）ξ统称为拟空间域采样间隔Δτ（φ）ξ，其中φ表示纵波p或横波s.

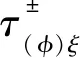
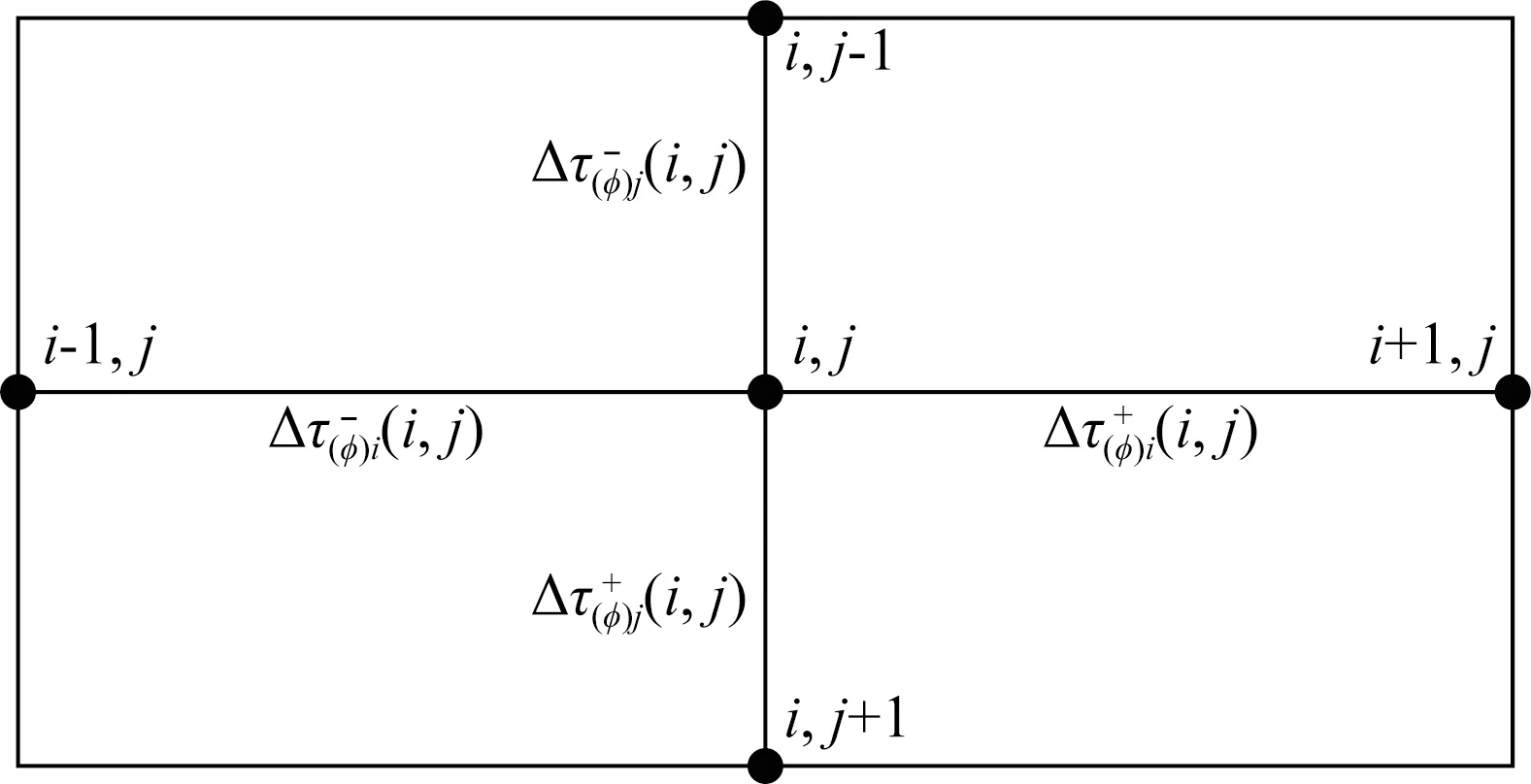
图3 网格模型中的任意一点P（i,j）周围有四个拟空间域采样间隔Fig.3 Four pseudo-space intervals around the point P（i,j）

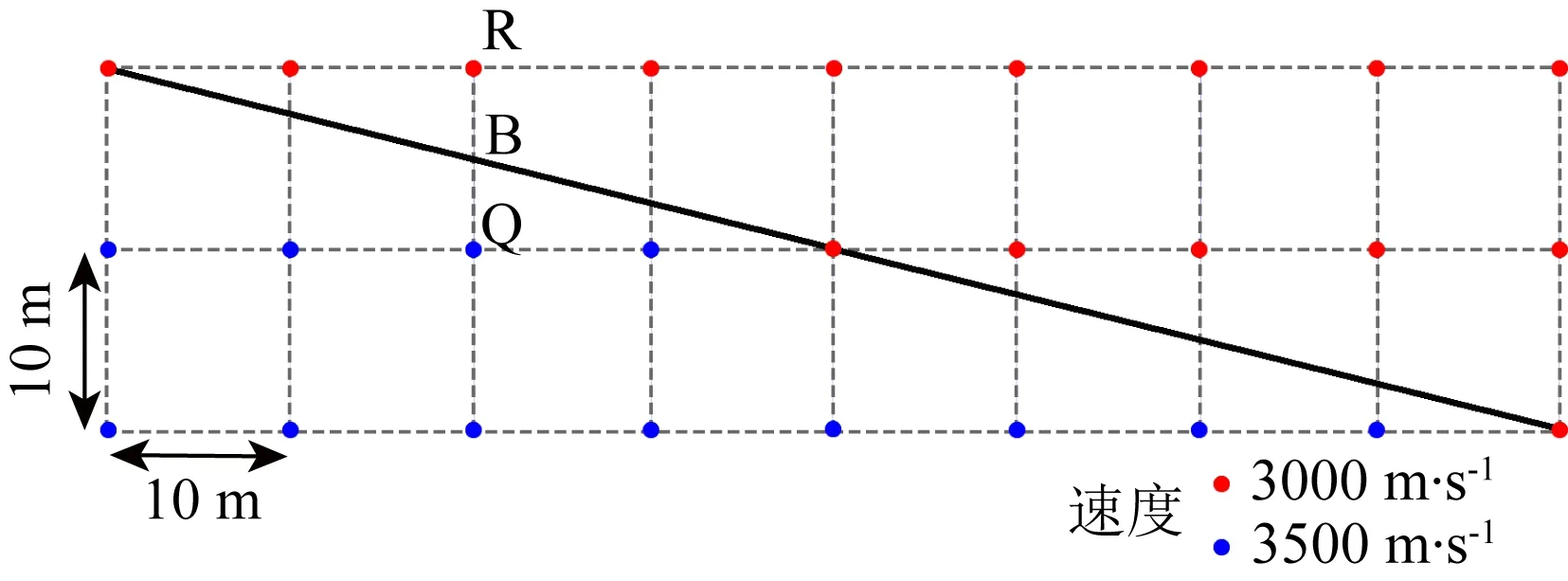
图4 倾斜速度界面的拟空间域采样间隔计算示意图Fig.4 Partial schematic illustration of a mesh model after the regular meshing of a velocity interface model including a slanted interface

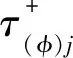
理论上讲，在拟空间域不再存在速度界面的畸变问题，甚至还会减弱相邻网格点之间模型参量的突变程度，从而可在偏移计算中期望降低假散射和界面反射.

2.2 拟空间域弹性波方程2N阶精度有限差分格式

基于拟空间域弹性波方程进行有限差分数值模拟时，为了提高模拟的精度，减少数值频散的影响，需要提高差分的精度，因此本文推导了拟空间域弹性波方程2N阶精度交错网格有限差分表达式.

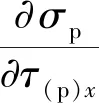
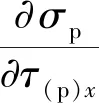
（6）

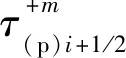
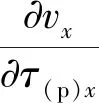
（7）

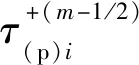
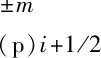
1,2,…,N-1,N）），在τ（p）x=τi+1/2处的2N阶Taylor级数展开式为：

（8）

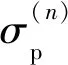
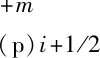
（9）

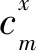
（10）

将式（10）求得的差分系数代入式（9）可以得到σp对变量τ（p）x在（τi+1/2,τj）处的一阶导数2N阶精度差分表达式：

（11）

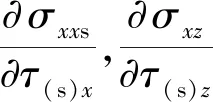
（12）

（12′）

其中k表示离散的时间点，满足t=kΔt（Δt表示离散时间步长）.

在中心波场计算区域，应用（12）式即可实现一阶速度-应力弹性波方程的时间二阶拟空间域2N阶精度有限差分数值模拟；而在人工边界区域，为有效压制人工边界反射，还需进行吸收边界处理，本文的数值实验均采用完全匹配层（Perfectly Matched Layer，PML）吸收边界条件（Collino and Tsogka,2001;任志明和刘洋,2014;张晓波等,2016;张晓波,2017）.

2.3 拟空间域一阶速度-应力弹性波方程稳定性条件

结合常规一阶速度-应力弹性波方程交错网格有限差分格式的稳定性条件（裴正林和牟永光,2003）以及平面谐波分析的方法，可以推导出一阶速度-应力弹性波方程拟空间域交错网格有限差分格式的稳定性条件.

首先定义拟空间域平面谐波变量u：

u=u0eiω nΔteikτxjΔτxeikτzkΔτz，

（13）

其中u0表示初始波场，ω代表圆频率，kτx和kτz分别代表关于τx和τz的波数，n、j和k分别代表t、τx和τz方向上离散网格点的坐标，Δτx和Δτz分别代表τx和τz方向上的拟空间域采样间隔，e代表自然对数的底，i代表虚数单位.根据式（13）可以得到：

（14）

将式（14）代入一阶导数差分格式表达式中为：

（15）

进而可得关于τx的二阶导数表达式：

（16）

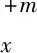
将式（17）中差分系数分别用关于τx的纵波和横波拟空间域差分系数代替，可得关于τx的纵波和横波拟空间域二阶导数表达式：

（18）

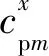
类似地，可推导出关于τz的纵波和横波拟空间域二阶导数表达式：

（19）

此外，关于时间t的二阶导数表达式可写为：

（20）

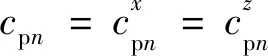
（21）

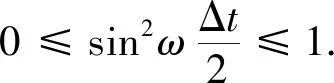
（22）

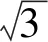
（23）

式中模型最大速度vmax=vp且Δh=Δx=Δz，将式（22）代入式（23）可以得到库朗数随差分阶数的变化关系，如图5所示.从图中可以看出，库朗数随着有限差分阶数的增加而减小，并且当阶数为2时，库朗数值小于1，符合数值计算的稳定性要求.

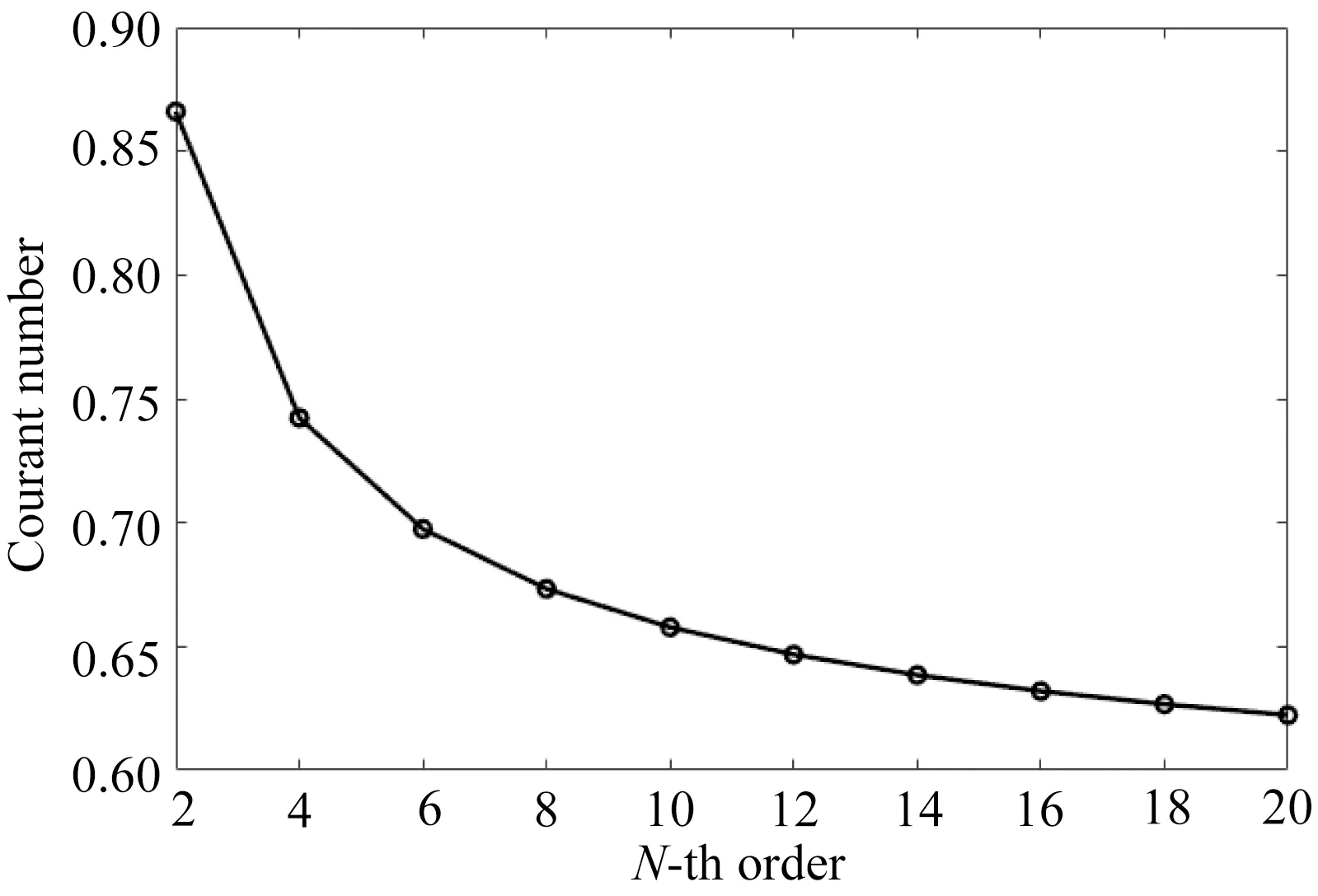
图5 库朗数随有限差分阶数的变化关系图Fig.5 Diagram of Courant number variation with finite difference orders

3 模型实验

3.1 归一化互相关成像条件

本文在逆时偏移中采用归一化互相关成像条件（Kaelin and Guitton,2006）实现偏移成像，其实现过程是利用正时波场的零延迟互相关的结果对正时波场与逆时波场零延迟互相关成像进行归一化处理（如式（24）和式（25）所示）.这里根据纵横波波场分离方法（李振春等,2007），对式（5）进行分解可以得到纵波波场vp={vxp,vzp}和横波波场vs={vxs,vzs}，其中vxp和vxs分别为水平速度分量vx的纵波波场和横波波场；vzp和vzs分别为垂直速度分量vz的纵波波场和横波波场.然后将纵横波分离后的波场代入式（24）和式（25）中，即可求出正时纵波波场和逆时纵波波场（PP 波）成像结果IPP和正时纵波波场和逆时横波波场（PS波）成像结果IPS.式（24）和式（25）为：

（24）

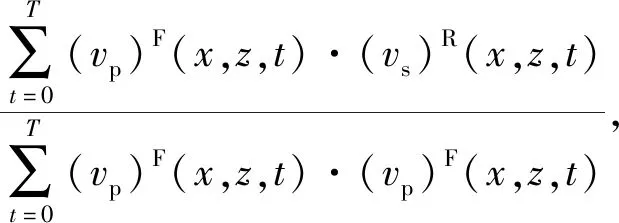
（25）

式中（vp）F为正时纵波波场，（vp）R为逆时纵波波场，（vs）R为逆时横波波场.

3.2 倾斜界面模型逆时偏移

本实验的主要目的是检验拟空间域声波方程逆时偏移在解决速度界面畸变以及压制界面假散射和层间反射波方面的有效性.

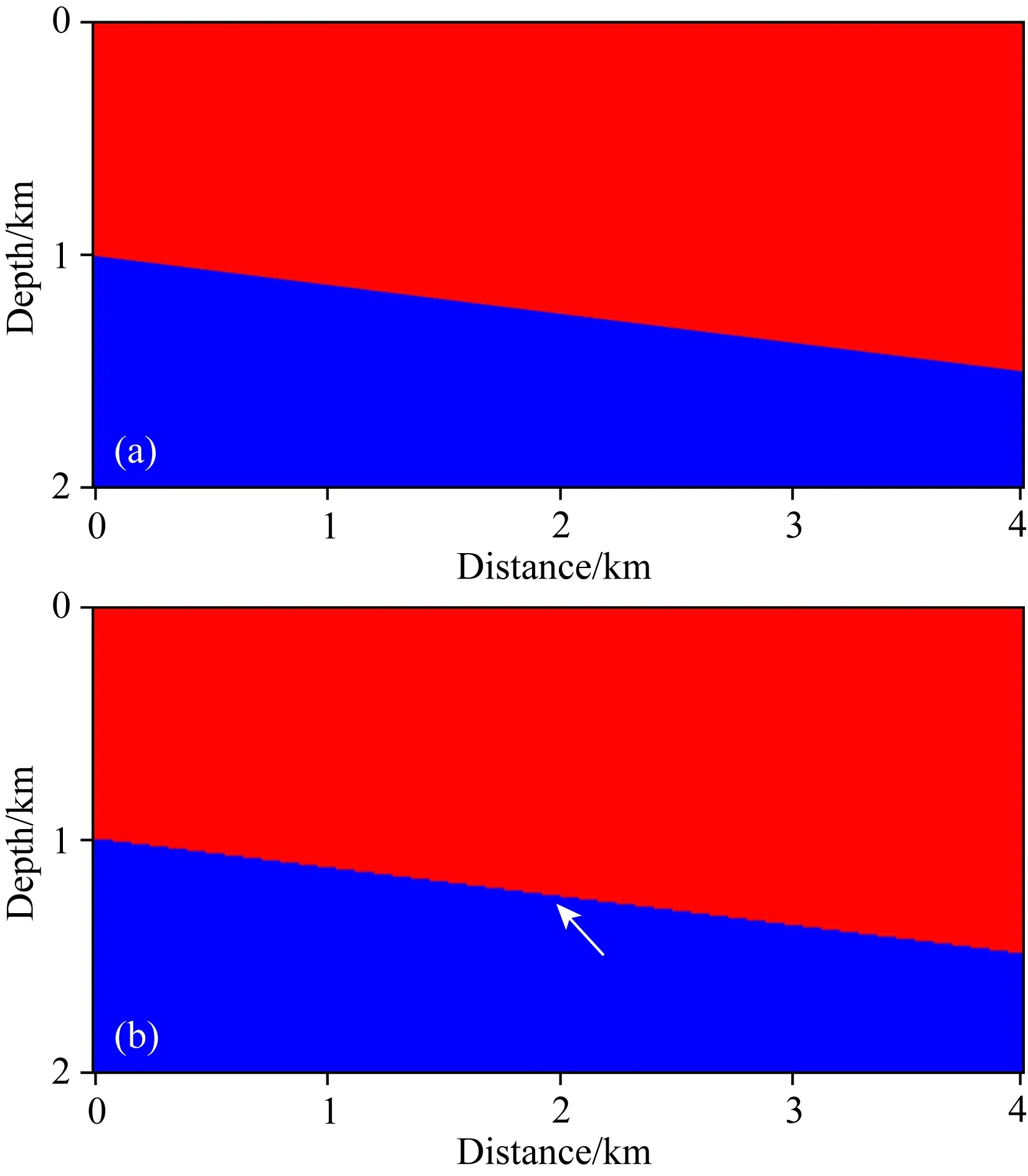
图6 含倾斜界面的两层速度模型（a） 原光滑界面模型；（b） 10 m网格间距的模型.Fig.6 Two-layer velocity model with a slanted interface（a） Original model with a smooth slanted interface;（b） Model with 10 m grid interval.

实验采用含有倾斜界面的两层速度模型，如图6a所示，其横向和纵向长度分别为4000 m和2000 m，界面上下两侧纵波速度分别为2500 m·s-1和3500 m·s-1，密度为2000 kg·m-3.将此倾斜界面模型以10 m的纵横向网格间距剖分后所得网格模型如图6b所示，可见原光滑的速度界面已变为明显的阶梯状界面（见图中白色箭头所指位置）.实验中建立道固定、炮移动的观测系统，炮点位于500 m至3480 m之间，炮间隔为20 m，共150炮；每炮接收道数为401道，各接收道位于0 m至4000 m之间，道间隔为10 m；炮点与接收点深度均为10 m.

采用纵波震源激发，而模型横波速度由纵波速度和泊松比值计算得到（本实验所用泊松比为0.25，密度为2000 kg·m-3）.正演模拟时采用主频为35 Hz的Ricker子波.为保证合成炮集记录的精度，模拟时纵横向网格间距均取为1 m，差分精度为时间二阶空间十六阶，共合成150炮地震记录，其中第76炮记录如图7所示.

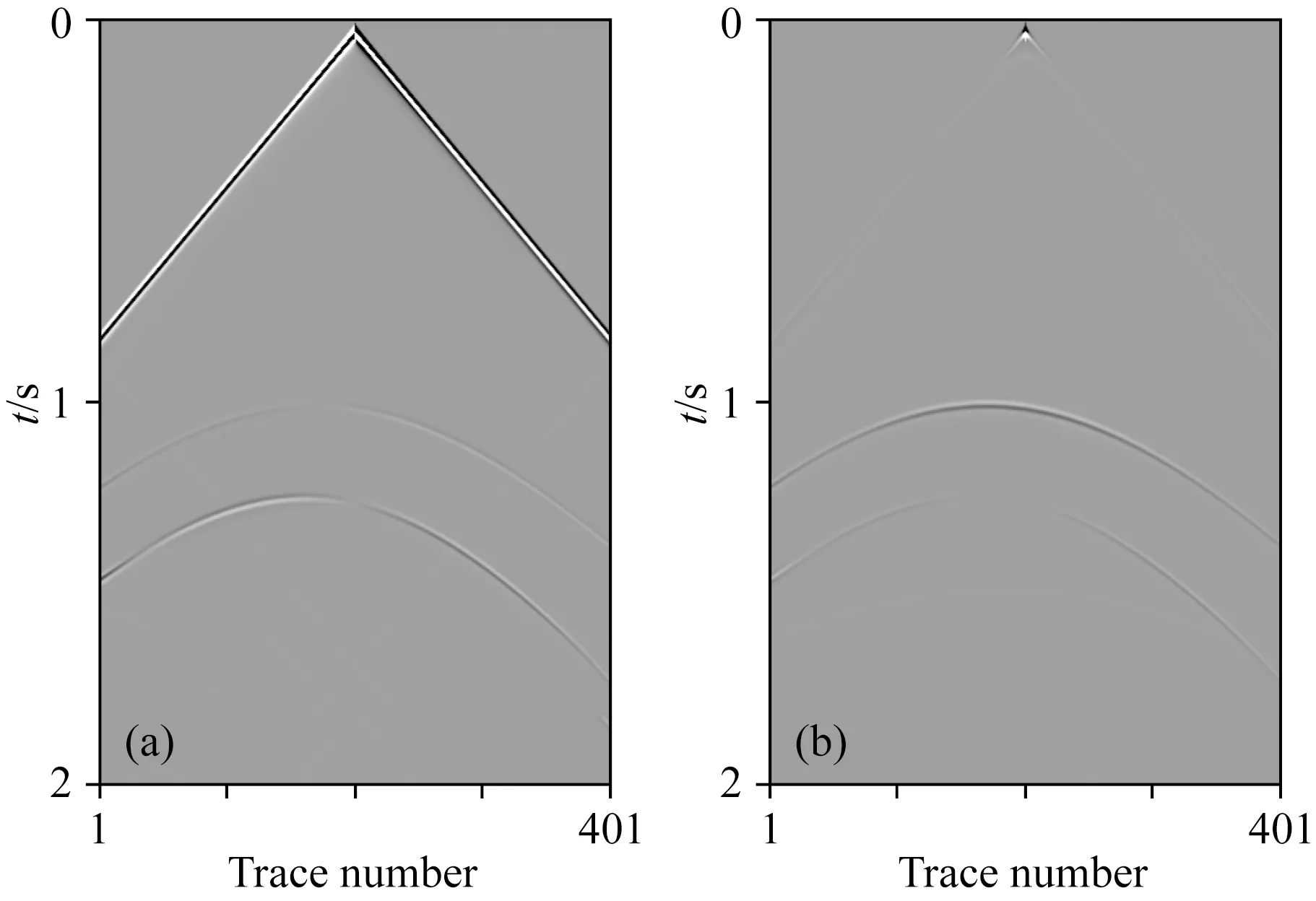
图7 合成炮集记录（第76炮）（a） 水平速度分量；（b） 垂直速度分量.Fig.7 Synthetic shot gather record example （76th shot gather）（a） Horizontal velocity component；（b） Vertical velocity component.

基于10 m网格间距模型分别进行常规弹性波方程和拟空间域弹性波方程有限差分（差分精度为时间二阶空间/拟空间十六阶）逆时偏移处理.图8显示了在0.9 s时刻第76炮的正时波场波前快照，图9则为获得的逆时偏移剖面.

从图8可以看出，常规弹性波方程的波场中存在明显的界面假散射（如图8a、c中椭圆区域所示）而拟空间域弹性波方程的波场中并无明显的界面假散射（如图8b、d中椭圆内区域所示）.对比图8中箭头处界面反射波可以看出，拟空间域弹性波方程对界面反射波（尤其是近垂直入射的反射波）压制明显.由此可以证明拟空间域弹性波方程在压制界面假散射和层间反射波方面的有效性.

为更直观的对比两种方法偏移剖面中倾斜界面的形态，对图9中椭圆区域内界面同相轴进行放大显示，如图10所示.可以看出，常规弹性波方程逆时偏移剖面中倾斜界面形态（图10a、c中红色虚线）相比于真实界面形态（图10a、c红色实线）出现明显畸变，而拟空间域弹性波方程逆时偏移剖面中倾斜界面的形态则与真实界面形态（图10b、d中红色实线）基本吻合.由此说明了拟空间域弹性波方程逆时偏移在解决界面畸变问题方面的有效性.

3.3 Marmousi模型逆时偏移

Marmousi模型是包含大量速度界面、陡倾角构造以及剧烈速度变化的复杂构造网格速度模型，模型横向和纵向长度分别为9200 m和3000 m，横纵向网格间距分别为5 m和4 m，模型横波速度由纵波速度和泊松比值计算得到（本实验所用泊松比为0.25，密度为2000 kg·m-3），纵波和横波速度模型如图11a、b所示.实验中采用右边放炮、左边接收的单边观测系统，共426炮，每炮104道接收，炮间隔和道间隔均为25 m，炮点和接收道深度均为8 m.采用纵波震源激发，震源子波采用主频为35 Hz的Ricker子波.通过常规弹性波方程有限差分方法（差分精度为时间二阶空间八阶）正演模拟合成426炮地震记录.

基于合成炮集记录，分别进行常规弹性波方程和拟空间域弹性波方程有限差分（差分精度为时间二阶空间/拟空间八阶）逆时偏移处理.图12显示了1.9 s时刻、第138炮的正时波场波前快照，图13则给出了相应的弹性波逆时偏移剖面.

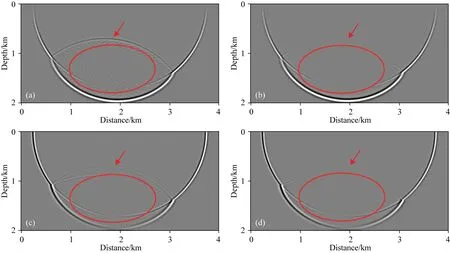
图8 逆时偏移正时波场波前快照（0.9 s时刻，第76炮）（a） 基于常规弹性波方程的垂直速度分量;（b） 基于拟空间域弹性波方程的垂直速度分量;（c） 基于常规弹性波方程的水平速度分量;（d） 基于拟空间域弹性波方程的水平速度分量.Fig.8 Snapshot of forward time wavefield in reverse time migration （76th shot at 0.9 s）（a） Vertical velocity component based on the conventional elastic wave equation;（b） Vertical velocity component based on the pseudo-space elastic wave equation;（c） Horizontal velocity component based on the conventional elastic wave equation;（d） Horizontal velocity component based on the pseudo-space elastic wave equation.

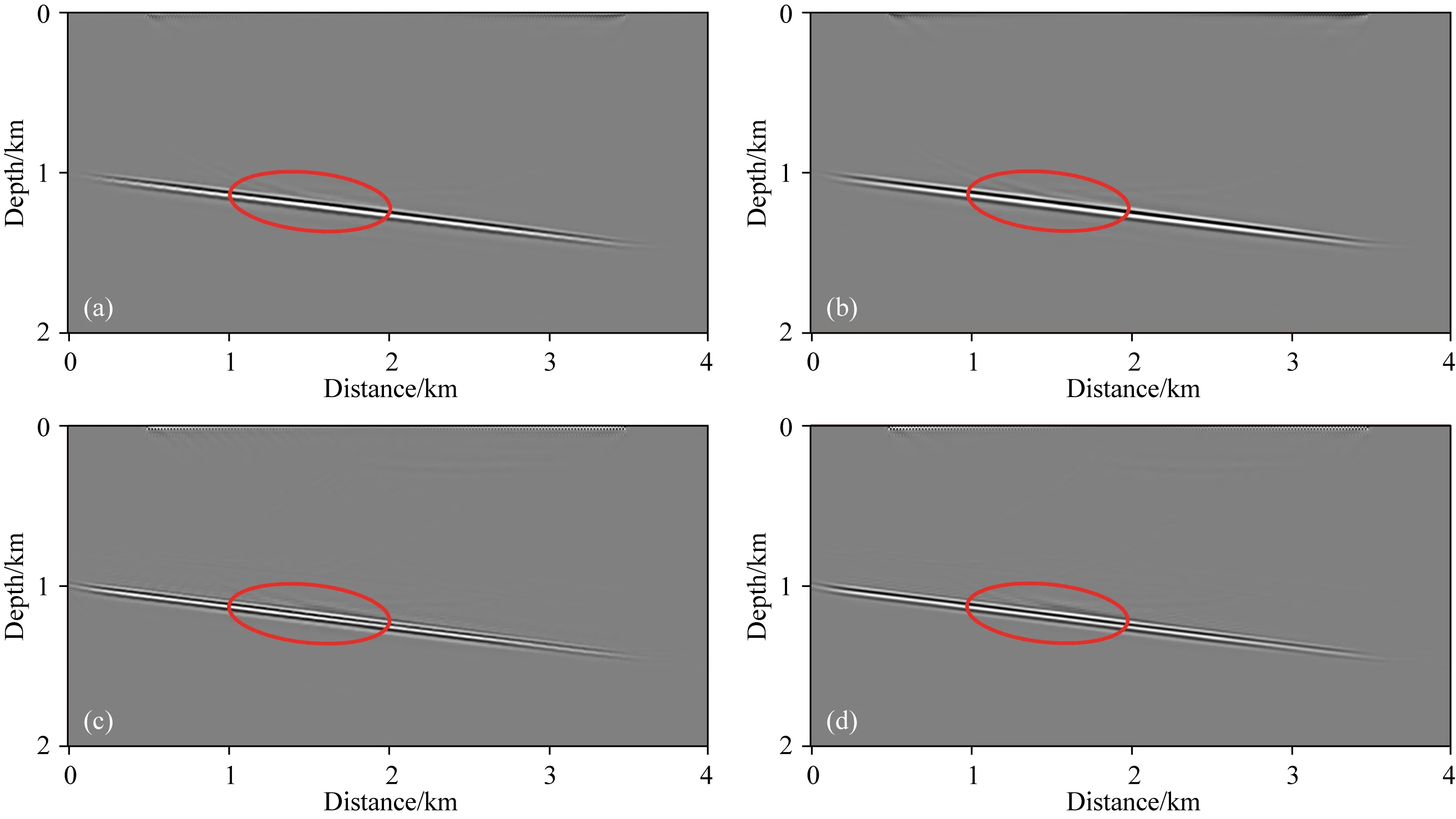
图9 逆时偏移剖面（a） 基于常规弹性波方程的IPP剖面；（b） 基于拟空间域弹性波方程的IPP剖面；（c） 基于常规弹性波方程的IPS剖面；（d） 基于拟空间域弹性波方程的IPS剖面.Fig.9 Profile of reverse time migration（a） IPP based on the conventional elastic wave equation；（b） IPP based on the pseudo-space elastic wave equation；（c） IPS based on the conventional elastic wave equation；（d） IPS based on the pseudo-space elastic wave equation.

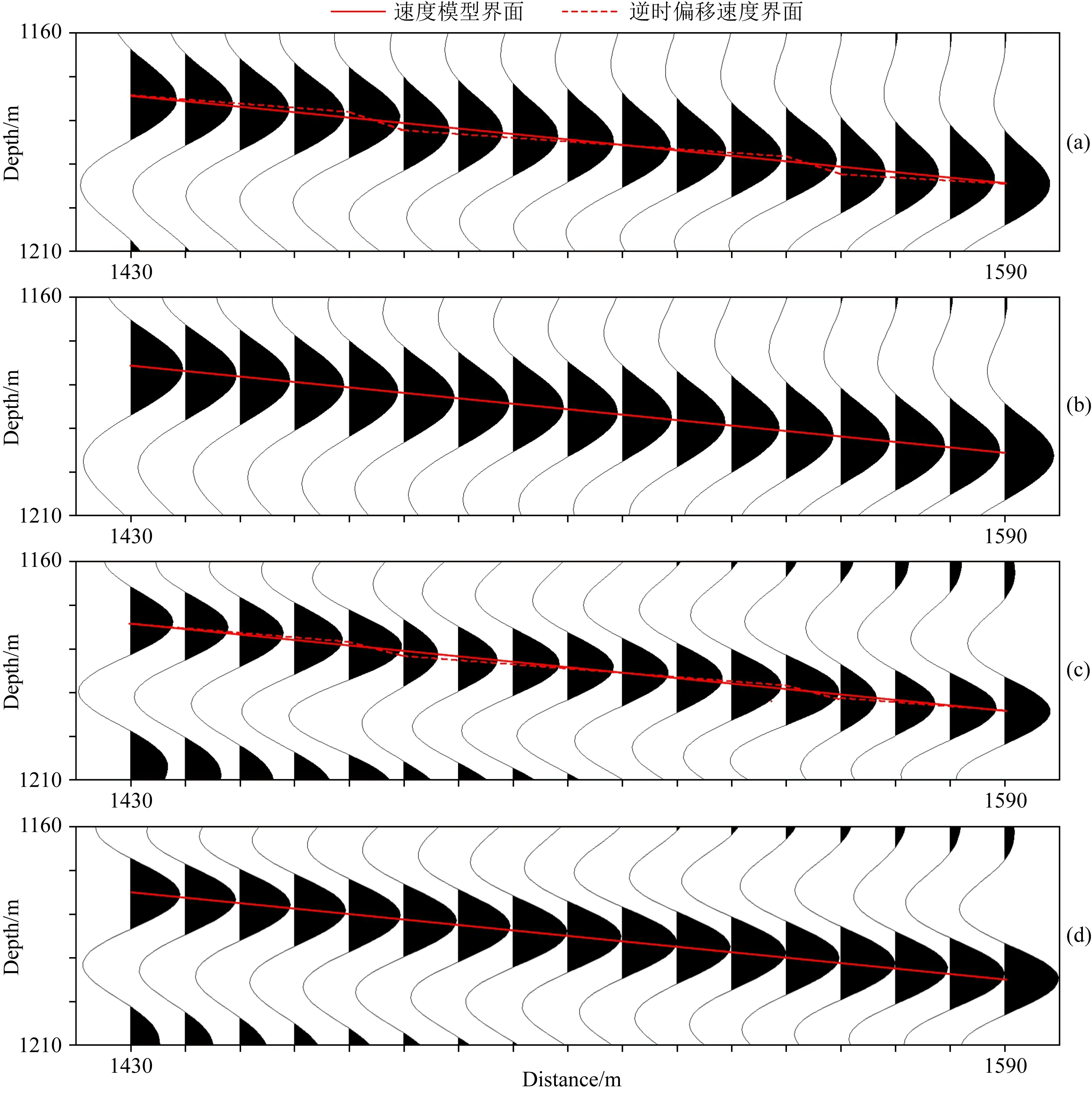
图10 逆时偏移地震剖面局部放大图示（a） 基于常规弹性波方程的IPP剖面；（b） 基于拟空间域弹性波方程的IPP剖面；（c） 基于常规弹性波方程的IPS剖面；（d） 基于拟空间域弹性波方程的IPS剖面.Fig.10 Local magnification of a reverse time migration profile（a） IPP based on the conventional elastic wave equation；（b） IPP based on the pseudo-space elastic wave equation；（c） IPS based on the conventional elastic wave equation；（d） IPS based on the pseudo-space elastic wave equation.

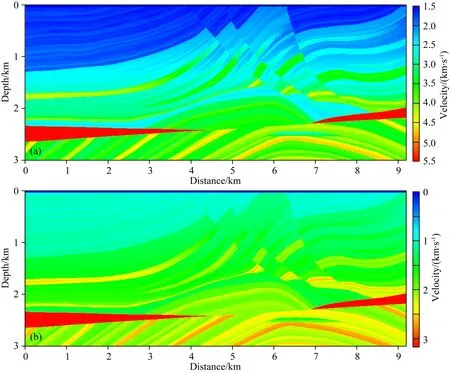
图11 Marmousi网格速度模型（a） 纵波速度模型；（b） 横波速度模型.Fig.11 Grid velocity model of Marmousi（a） Primary velocity model；（b） Shear velocity model.

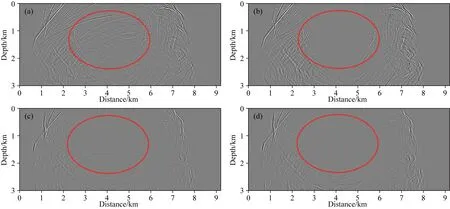
图12 Marmousi模型逆时偏移正时波场波前快照（1.9 s时刻，第138炮）（a） 基于常规弹性波方程的垂直速度分量;（b） 基于拟空间域弹性波方程的垂直速度分量;（c） 基于常规弹性波方程的水平速度分量;（d） 基于拟空间域弹性波方程的水平速度分量.Fig.12 Forward time wavefield wavefront snapshot in reverse time migration for the Marmousi model （138th shot at 1.9 s in time）（a） Vertical velocity component based on the conventional elastic wave equation;（b） Vertical velocity component based on the pseudo-space elastic wave equation;（c） Horizontal velocity component based on the conventional elastic wave equation;（d） Horizontal velocity component based on the pseudo-space elastic wave equation.

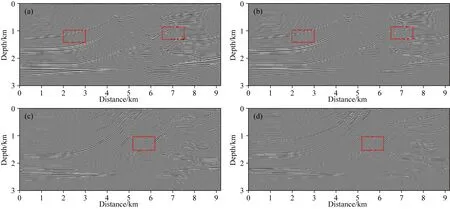
图13 Marmousi模型弹性波逆时偏移剖面（a） 基于常规弹性波方程的IPP剖面；（b） 基于拟空间域弹性波方程的IPP剖面；（c） 基于常规弹性波方程的IPS剖面；（d） 基于拟空间域弹性波方程的IPS剖面.Fig.13 Reverse time migration profiles for the Marmousi model（a） IPP based on the conventional elastic wave equation；（b） IPP based on the pseudo-space elastic wave equation；（c） IPS based on the conventional elastic wave equation；（d） IPS based on the pseudo-space elastic wave equation.

图14 Marmousi模型弹性波逆时偏移地震剖面局部放大图示（a） 网格模型；（b） 基于常规弹性波方程；（c） 基于拟空间域弹性波方程.Fig.14 Local magnification of reverse time migration profiles for the Marmousi model （a） Grid model；（b） Based on the conventional elastic wave equation；（c） Based on the pseudo-space elastic wave equation.

由图12可见，与常规弹性波方程逆时偏移相比，拟空间域弹性波方程逆时偏移波场中层间反射波明显减弱（如图12中红色椭圆区域所示），这同样显示出拟空间域弹性波方程在复杂构造模型波场延拓时压制层间反射波的有效性.

为更好地对比逆时偏移的效果，将图13中红色矩形区域内的局部偏移剖面进行放大显示（如图14所示）.可以看出，与常规弹性波方程逆时偏移相比，拟空间域弹性波方程逆时偏移所得剖面中构造清晰、同相轴连续性更好（红色箭头处所示），从而说明拟空间域弹性波方程逆时偏移的成像质量要优于常规弹性波方程逆时偏移.

4 结论与展望

本文深入讨论了拟空间域弹性波方程的原理，在此基础上，推导了拟空间域弹性波方程高阶有限差分格式，并给出了差分格式的稳定性条件，实现了高精度的拟空间域弹性波方程逆时偏移.理论分析和模型实验得出结论如下：

（1） 本文推出的高阶有限差分格式能够实现拟空间域弹性波方程的高精度波场延拓，并且其适用于复杂构造模型.

（2） 若在计算拟空间采样间隔时引入速度界面信息，则拟空间域弹性波方程高阶有限差分逆时偏移能够避免常规弹性波方程逆时偏移中弯曲界面形态畸变问题；此外基于该方法进行波场延拓时可有效压制弯曲界面的假散射问题，并能显著降低层间反射波，因此可以减少剖面上的偏移假象，从而显著提高成像的质量.

当然，目前拟空间域弹性波方程高阶有限差分逆时偏移方法对于非垂直入射的层间反射波压制效果尚不理想，因此进一步改进该方法的层间反射波压制效果，提高逆时偏移成像的精度，并将其发展到三维波动方程的逆时偏移中将是下一步的研究工作.